Modelling and prediction of the thermophysical properties of aqueous mixtures of choline geranate and geranic acid (CAGE) using SAFT-γ Mie

Abstract

Deep-eutectic solvents and room temperature ionic liquids are increasingly recognised as appropriate materials for use as active pharmaceutical ingredients and formulation additives. Aqueous mixtures of choline and geranate (CAGE), in particular, have been shown to offer promising biomedical properties but understanding the thermophysical behaviour of these mixtures remains limited. Here, we develop interaction potentials for use in the SAFT-γ Mie group-contribution approach, to study the thermodynamic properties and phase behaviour of aqueous mixtures of choline geranate and geranic acid. The determination of the interaction parameters between chemical functional groups is carried out in a sequential fashion, characterising each group based on those previously developed. The parameters of the groups relevant to geranic acid are estimated using experimental fluid phase-equilibrium data such as vapour pressure and saturated-liquid density of simple pure components (n-alkenes, branched alkenes and carboxylic acids) and the phase equilibrium data of mixtures (aqueous solutions of branched alkenes and of carboxylic acids). Geranate is represented by further incorporating the anionic carboxylate group, COO⁻, which is characterised using aqueous solution data of sodium carboxylate salts, assuming full dissociation of the salt in water. Choline is described by incorporating the cationic quaternary ammonium group, N⁺, using data for choline chloride solutions. The osmotic pressure of aqueous mixtures of CAGE at several concentrations is predicted and compared to experimental data obtained as part of our work to assess the accuracy of the modelling platform. The SAFT-γ Mie approach is shown to be predictive, providing a good description of the measured data for a wide range of mixtures and properties. Furthermore, the new group-interaction parameters needed to represent CAGE extend the set of functional groups of the group-contribution approach, and can be used in a transferable way to predict the properties of systems beyond those studied in the current work.

The properties of aqueous solutions of the CAGE deep eutectic solvent are predicted with the SAFT-γ Mie approach.

1. Introduction

Deep-eutectic solvents (DESs) and room temperature ionic liquids (RTILs) are increasingly recognised as advantageous materials for use as carriers of active pharmaceutical ingredients and formulation additives.^1–3 DESs exhibit physical properties which are similar to those of conventional ILs such as low volatility over a relatively wide liquid range and non-flammability, and as such can be considered as a new class of ionic liquids.² In terms of definition, the only difference between RTILs and DESs is the ratio of the components in the mixtures. RTILs are usually defined as organic salts with 1 : 1 cation : anion molar ratio and melting points below 100 °C, while DESs are more generally defined as mixtures of charged and neutral components. A series of studies of DESs/RTILs for a number of anion/cation/solvent combinations have been tested,^4–7 and mixtures of choline and generate (CAGE) were shown to offer promising therapeutical properties, including powerful antibacterial activity against a variety of drug-resistant bacteria, fungi and viruses, low toxicity, and enhancement of the transdermal delivery of proteins and antibacterial drugs. The mixture with a 1 : 2 choline : geranate mol ratio was shown to be especially effective.^4,8

Following these findings, it is of interest to develop a better understanding of CAGE mixtures through the acquisition of new data and the development of molecular models capable of delivering accurate estimates and predictions of the physical properties of CAGE and its aqueous solutions, as these are immediately relevant to further biomedical applications and are needed to facilitate process modelling for the manufacture of medicinal products based on this solvent. Available work relating to the physical properties of CAGE is, however, currently limited. Mitragotri and co-workers have presented molecular-dynamics simulations with all-atom and coarse-grained force fields to study the structural properties of CAGE in the presence of water,⁹ and its activity on the cell membrane of Gram-negative E. coli in the absence of water.⁷ A key finding of the experiments and molecular-dynamics simulations studies thus far is that water molecules can induce changes in the structure of CAGE for mole fractions of water higher than ∼0.65. As the amount of water in the solutions increases, the hydrogen bonds between choline and geranate are disrupted and the formation of microstructures between geranic acid molecules is promoted.⁹

In addition to molecular-dynamics simulations, molecular-based equations of state are useful tools to study and predict the thermodynamic properties of complex fluid mixtures. The perturbed-chain statistical associating fluid theory (PC-SAFT)¹⁰ has been shown to describe accurately the solid–liquid equilibria of a number of DESs^11–13 and the liquid–liquid equilibria data of several RTILs.^14–16 In these studies, short-range association sites were used to mimic hydrogen bonding interactions between species but the anion and cation were not treated as explicitly charged species. In aqueous solutions, the presence of charged species critically affects the thermodynamic properties of the mixtures. Thus, accounting for coulombic interactions is expected to provide a better description of the physical properties and lead to more predictive models of these complex systems.

The SAFT-γ Mie group-contribution approach^17,18 is a recently developed version of the SAFT family of equations of state, based on a Mie (generalised Lennard-Jones) potential of variable repulsive and attractive range. In this approach, the group-contribution premise that the properties of a molecule or mixture can be determined by accounting for the appropriate contributions of the chemical moieties (functional groups) in the system of interest is adopted. The parameters describing the functional groups (methylene CH₂, methyl CH₃, carboxyl COOH, etc.) and their interactions are derived in a sequential manner, with the determination of each new group–group interaction based on that of previous groups. From the characterisation of a relatively small number of groups it is then possible to evaluate the properties of a much larger set of systems, including mixtures. The approach has been shown to be accurate for the prediction of thermodynamic properties, phase equilibria (vapour–liquid, liquid–liquid, and solid–liquid) of complex mixtures,¹⁸ as well as for the solubility and octanol–water partition coefficients of organic molecules of interest in pharmaceutical applications.¹⁹ Of particular relevance to this discussion is the fact that charged compounds can be accounted for in the methodology.^20,21 Furthermore, the SAFT-γ Mie approach has the added advantage of maintaining a direct link between the molecular model and the corresponding macroscopic equilibrium properties, which allows it to be used for the development of force-field parameters for use in molecular simulation,^22,23 from which structural, interfacial and transport properties can also be studied.

Given the importance of CAGE, we present here new experimental data for the osmotic pressure of aqueous solutions of CAGE and develop appropriate functional group models for use within the SAFT-γ Mie platform relevant to the molecules in the CAGE mixture. Further, we demonstrate that our group-contribution approach delivers accurate predictions of the osmotic pressure. Details of the experimental and theoretical methodologies are presented in the following section, with results reported in Section 3, and conclusions in Section 4.

2. Methods

2.1. Experimental

¹H NMR and ¹³C¹H NMR spectra were obtained on a Bruker Avance 400 spectrometer at 298 K and referenced to the residual solvent signal. DEPT-135 and 2D correlation spectra were used to aid assignments but have not been otherwise documented. (CD₃)₂SO was bought from Sigma and used as received. Mass spectra were obtained by directly injecting CAGE into a Waters single quadrupole detector at 4.2 kV capillary voltage. The IR spectrum was run on a PerkinElmer Spectrum 100 using an ATR attachment. Elemental analysis was carried out by Stephen Boyer (London Metropolitan University).

A sample of CAGE was prepared following the procedure described by Zakrewsky et al.⁴ Choline bicarbonate (80 wt% solution in water, 2.68 g, 13.72 mmol) was purchased from Sigma and used as received. Geranic acid (85%) was purchased from Sigma and was recrystallised five times from cold HPLC-grade acetone (VWR) before use. A solution of choline bicarbonate (80 wt% in water, 2.68 g, 13.72 mmol) was diluted further with water (4 mL), then added to neat geranic acid (4.62 g, 27.43 mmol). The reaction was stirred until CO₂ evolution ceased (3 hours). Water was then removed by azeotrope with toluene under reduced pressure. The resulting colourless viscous oil was dried under high vacuum at 40 °C for 16 hours (yield 6.02 g, 100%).

¹H NMR (400.1 MHz, (CD₃)₂SO): 10.19 (v br s, [2H], OH), 5.57 (d, J = 1.2 Hz, [2H], H2), 5.07 (br t, J = 6.5 Hz, [2H], H6), 3.83–3.88 (m, [2H], H2′), 3.41–3.46 (m, [2H], H1′), 3.13 (s, [9H], H3′), 1.95–2.10 (m, [14H], H4, H5, H9), 1.64 (s, [6H], H8/10), 1.56 (s, [6H], H8/10) ppm.

¹³C¹H NMR (100.6 MHz, (CD₃)₂SO): 169.92 (C, C1), 148.22 (C, C3), 130.96 (C, C7), 123.74 (CH, C6), 122.36 (CH, C2), 67.22 (CH₂, C1′), 55.01 (CH₂, C2′), 53.07 (t, J = 3.5 Hz, CH₃, C3′), 39.87 (CH₂, C4), 25.83 (CH₂, C5), 25.43 (CH₃, C9), 17.61 (CH₃, C8/10), 17.48 (CH₃, C8/10) ppm.

IR (ATR): 2968, 2915, 1694, 1646, 1548, 1479, 1437, 1397, 1375, 1317, 1228, 1158, 1088, 1055, 1006, 954, 867, 821, 692 cm⁻¹.

MS (positive ion): m/z 104.2 ([choline]⁺, 100%), 207.4 ([(choline)₂–H]⁺, 33%), 375.5 ([(choline)₂ + geranate]⁺, <5%), 478.6 ([(choline)₃ + geranate–H]⁺, <5%), 646.7 ([(choline)₃ + (geranate)₂]⁺, <5%), 749.8 ([(choline)₄ + (geranate)₂–H]⁺, <5%), 917.8 ([(choline)₄ + (geranate)₃]⁺, <5%). (Negative ion): m/z 167.2 ([geranate]⁻, 90%), 335.4 ([H(geranate)₂]⁻, 5%), 438.5 ([CAGE–H]⁻, 100%), 709.6 ([CAGE + choline + geranate]⁻, <5%), 980.7 [CAGE + (choline)₂ + geranic acid + geranate]⁻, <5%.

Analysis calc. for C₂₅H₄₅NO₅ (439.33): C 68.29; H 10.32; N 3.19. Found: C 68.33; H 10.45; N 3.14.

Copies of the corresponding NMR, IS and MS spectra can be found in the ESI.†

CAGE solutions were prepared with de-ionised, distilled water (Honeywell lot DT295-B-US) from serial dilutions of a solution obtained by mixing CAGE liquid and water. The concentration was adjusted for water content, which was estimated from thermal gravimetric analysis of the CAGE mixture immediately prior to use. Thermal gravimetric data was generated using a TA Instrument TGA Discovery series (2.2489 mg, 10 °C min⁻¹, 22.5 to 350 °C). Aliquots (10 μL) of each solution were analysed in triplicate on the same day as preparation using a Wescor vapour-pressure osmometer VAPRO model 5600 calibrated with 290, 100 and 1000 mmol kg⁻¹ standards (Optimole™). The osmotic pressure, Π = cRT was determined from the measured osmotic concentrations c, with R the gas constant and T the temperature.

2.2. SAFT-γ Mie model and theory

In the SAFT-γ Mie group-contribution approach^17,18 molecules are represented as associating hetero-segmented chains consisting of fused spherical segments that interact via Mie potentials of variable range²⁴ with short-range directional interactions incorporated by embedding square-well association sites on any given segment. The total Helmholtz free energy A of a mixture of n components at a given temperature T, volume V, and composition vector N = (N₁, N₂, …, N_n), where N_j denotes the number of molecules of component j, is obtained as the sum of six contributions arising from a perturbation approach:^17,18,20

A = A^ideal + A^monomer + A^chain + A^association + A^Born + A^ion. 1

Here, A^ideal represents the contribution of the ideal gas mixture of non-interacting particles and point charges, and A^monomer, A^chain and A^association are the usual residual non-electrostatic terms describing the change in free energy associated with the monomer spherical segments interacting through Mie potentials, the contribution due to fusing monomer spherical segments into molecular chains, and the contribution due to molecular association through the short-ranged square-well sites, respectively. The terms A^Born and A^ion represent the residual electrostatic terms accounting for the process of charging the ions in the solvent following the Born model²⁵ and the coulombic interactions between charged species which are treated with the primitive non-restricted mean-spherical approximation.^26,27 A detailed description of the theory and complete expressions for each of the contributions can be found in ref. 17, 18, 20 and 21.

A given chemical functional group k is characterised by a number 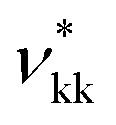of identical spherical segments and a shape factor, S_kk (0 ≤ S_kk ≤ 1), which represents the contribution made by each group to the overall free energy of the molecule considered. The interaction between two groups k and l is described using the Mie potential:²⁴

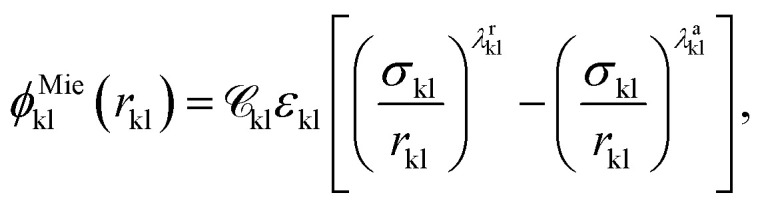2

where r_kl is the distance between the centres of the two segments, σ_kl the segment diameter, ε_kl the depth of the potential, and λ^r_kl and λ^a_kl are the repulsive and attractive exponents of the interaction between the segments, respectively. 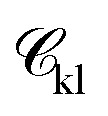is a function of the Mie potentials exponents:

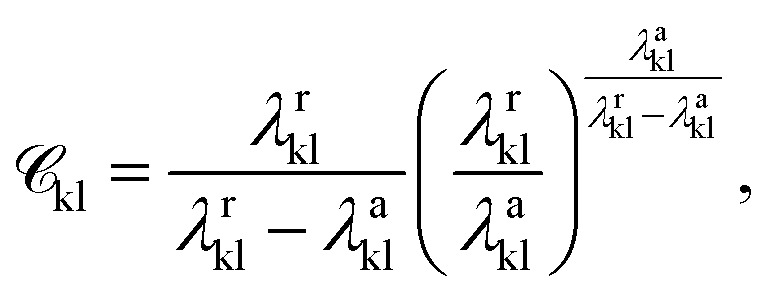3

which ensures that the minimum of the interaction potential is −ε_kl. The attractive exponent λ^a_kk is typically set to the London dispersion value of 6. Short-range square-well association sites are used to model strong polar interactions such as hydrogen bonding. These association sites are placed on any given segment where appropriate. A segment k may have any number N_ST,k of different association site types, with n_k,a sites of type a = 1, …, N_ST,k. Considering two square-well association sites of type a in segment k and b in segment l, respectively, the association interaction between them is given by

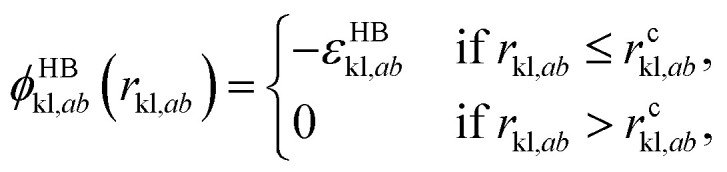4

where r_kl,ab is the distance between the centres of two sites, ε^HB_kl,ab is the association energy, and r^c_kl,ab the cut-off range of the interaction between sites a and b on groups k and l. Each site is positioned at a distance r^d_kk,ab from the centre of the segment on which it is placed; the cut-off distance r^c_kl,ab can equivalently be described in terms of a bonding volume K^HB_kl,ab for a given value of r^d_kk,ab.

The model parameters characterising the interactions between unlike functional groups k and l can be obtained through combining rules in the first instance. The unlike segment diameter σ_kl is obtained using a Lorentz-like arithmetic mean of the like diameters,²⁸i.e.,

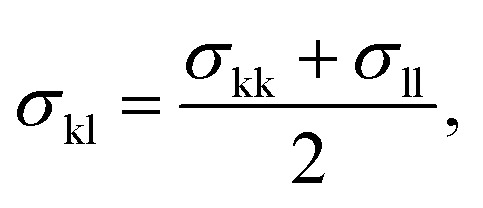5

the exponents of the unlike segment–segment interaction λ^r_kl and λ^a_kl can be obtained as¹⁷

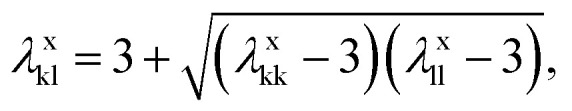6

where x = (r, a), and the unlike dispersion energy parameter between uncharged groups as

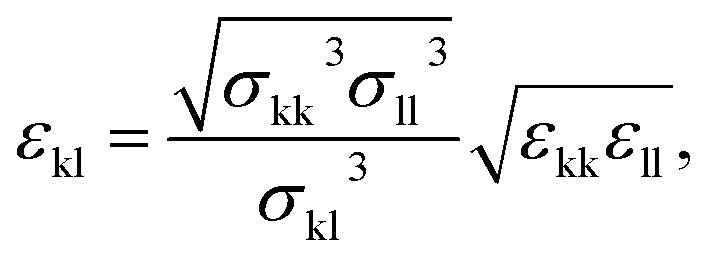7

following a Berthelot-like geometric mean rule, which accounts for differences in the size of the segments. The bonding volume K^HB_kl,ab and association energy parameter ε^HB_kl,ab between unlike sites can also calculated following arithmetic and geometric averages as

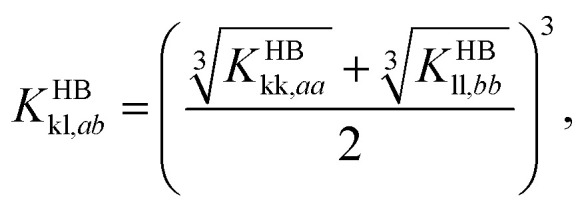8

and

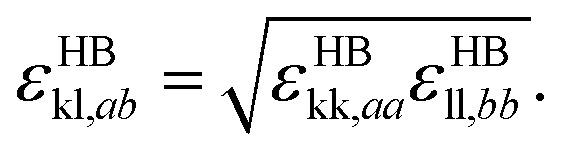9

These combining rules provide a useful first estimate of the values of these parameters. In practice, however, the unlike dispersion energy and repulsive exponent, as well as the unlike association energy and bonding volume are typically estimated by comparison to target experimental thermophysical properties of substances belonging to chemical families or mixtures in which the functional group is present.

In the case of charged groups, a value for the Born cavity diameter, σ^Born_kk, also has to be specified. This is taken from previous work, for known groups, or assigned a value following the Rashin and Honig²⁹ recipe (σ^Born_kk = 1.07σ_kk). In addition, the unlike dispersion energy parameter between charged groups is obtained using²⁰

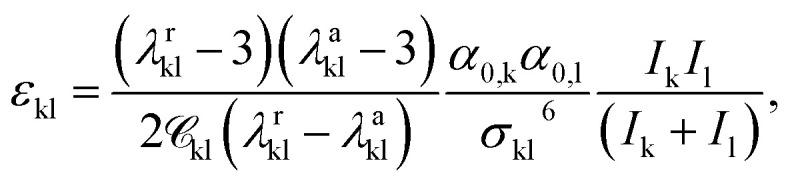10

which takes into account the polarisability, α₀, and the electron affinity, I, of the charged functional groups. These values are generally taken from published values.

2.3. Thermodynamic properties

Standard thermodynamic relations and phase-equilibrium conditions are applied to calculate a range of equilibrium thermodynamic properties such as the vapour pressure and saturated-liquid density of pure substances and the mean ionic activity coefficients, osmotic coefficients and osmotic pressures of the solutions.

The pressure and chemical potential μ_i^V = μ_i(T, V, N) of a component i are obtained from the Helmholtz free energy at given T, V and N as

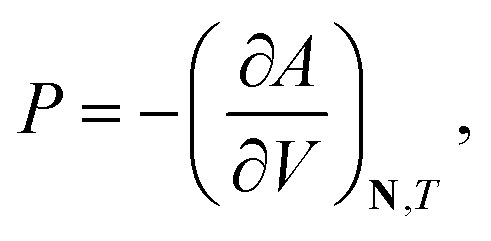11

and

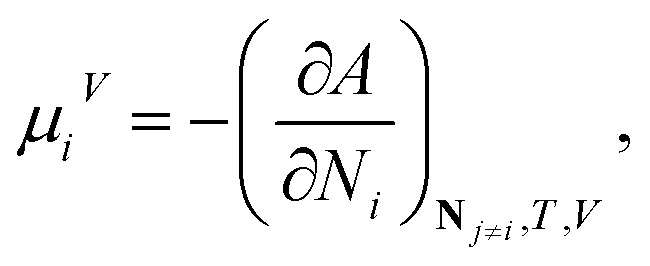12

respectively. In practice, it is more convenient to specify the pressure of the system than its volume, and the activity coefficient of component i, γ_i,x, is related to a chemical potential μ_i^P = μ_i(T, P, N) according to:

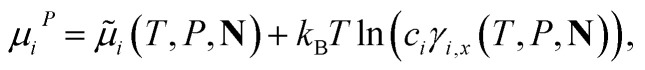13

where _i(T, P, N) is the chemical potential of the reference term of component i, k_B the Boltzmann constant, and c_i the concentration of component i; the subscript x denotes that γ_i,x is expressed in units commensurate with those of c_i. It is often convenient to measure the concentration in terms of the mole fraction x_i of the component and to refer to the standard symmetrical activity coefficient expressed in terms of x_i. The reference term of the chemical potential _i(T, P, N) is identical to the chemical potential of pure component i at the same thermodynamic conditions, i.e., _i = μ⁰_i(T, P).

For ionic species, the chemical potential is expressed using an asymmetric convention in which the activity coefficient γ_i,* has a value equal to one in the limit of infinite dilution; due to electroneutrality, a pure ion does not exist in an isolated state, so that ionic species cannot be related to a pure one-component system. In practice, this activity coefficient is calculated using the fugacity coefficient at the specified system conditions φ_i(T, P, N), normalised by the fugacity coefficient at infinite dilution, 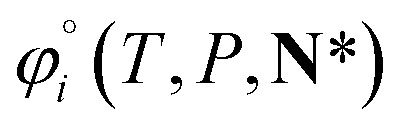, i.e.,

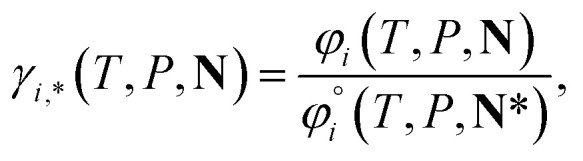14

where N* is the composition vector at infinite dilution of ion i. The fugacity coefficient is calculated through the chemical potential, which can be obtained using the equation of state:

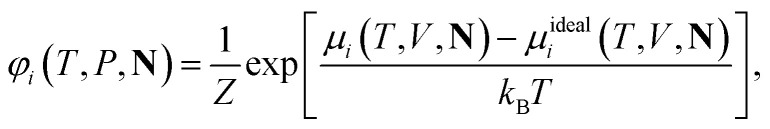15

where Z is the compressibility factor, Z = PV_P/(Nk_BT), V_P is the volume corresponding to the specified pressure, N the total number of molecules in the system, and μ^ideal_i(T, V, N) the chemical potential of i in the ideal gas mixture. The mean activity coefficient of the salt is often used, defined as

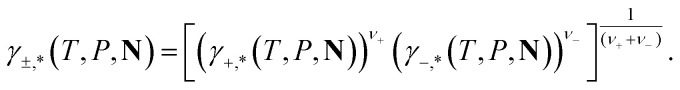16

where ν₊ and ν₊ are the stoichiometric coefficients of the cation and anion. A change to a molal-based scale can be carried out using γ_±,m(T, P, N) = x_jγ_±,*(T, P, N) where x_j is the mole fraction of the solvent.

The osmotic coefficient, Φ(T, P, N), of a solution is obtained by calculating the activity coefficient of the solvent j from the following equation:

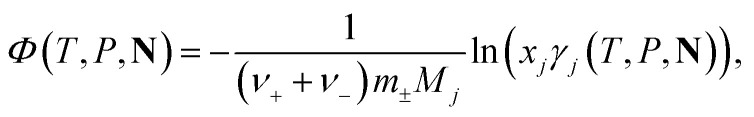17

where m_± refers to the molarity of the salt, and x_j and M_j are the mole fraction and the molecular weight of the solvent, respectively. The osmotic pressure Π is predicted using the Van't Hoff equation considering the fluid, at temperature T, to be incompressible:

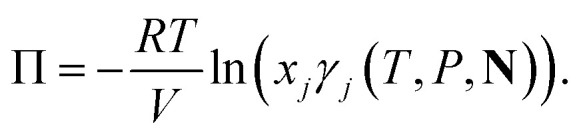18

The liquid–liquid and vapour–liquid equilibria are obtained by imposing thermal, mechanical, and chemical equilibrium across the different phases, i.e., the temperature, pressure, and chemical potential of each component in each phase are set to be equal. The vapour pressure is calculated assuming that the charged species are non-volatile. The equality of chemical potential is imposed for each neutral species in all the phases considered (α, β, …, N_phase):

μ_j^α = μ_j^β = … = μ_j^N_phase. 19

For each pair of charged species, i and i′, the fluid-phase equilibrium is imposed as described in ref. 20 and 30:

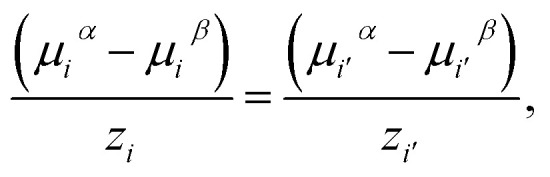20

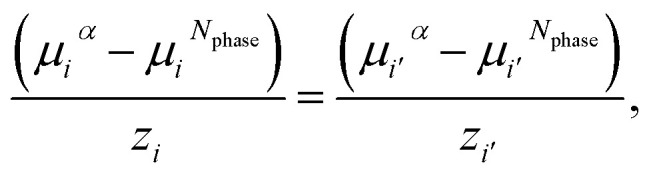21

where z_i and z_i′ are the valencies of ions i and i′, respectively.

We use the percentage average absolute deviation (% AAD_R) of a property R,

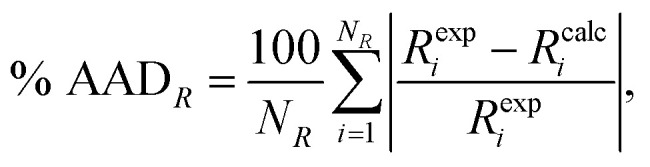22

as a measure of the accuracy of the theoretical description for any given thermophysical property R^calc_i with respect to the experimental data R^exp_i calculated at the thermodynamic state i, where N_R is the number of data points of the property of interest. The parameter estimation is performed using the gPROMS software package.³¹

3. Results and discussion

In order to model CAGE with the SAFT-γ Mie approach all of the relevant group-interaction parameters have to be determined. Functional groups are developed in a successive manner, with the characterisation of new group based on that of previously determined values.

Each component of the mixture is decomposed into its functional groups, with the assumption that the properties of the solution can be determined as appropriate functions of the chemically distinct functional groups that the compounds comprise and, that the contribution of each functional group to the molecular properties is independent of the molecular structure in which the group appears (see Fig. 1). One should also note that in the case of small molecules such as water, the entire molecule constitutes also a group.

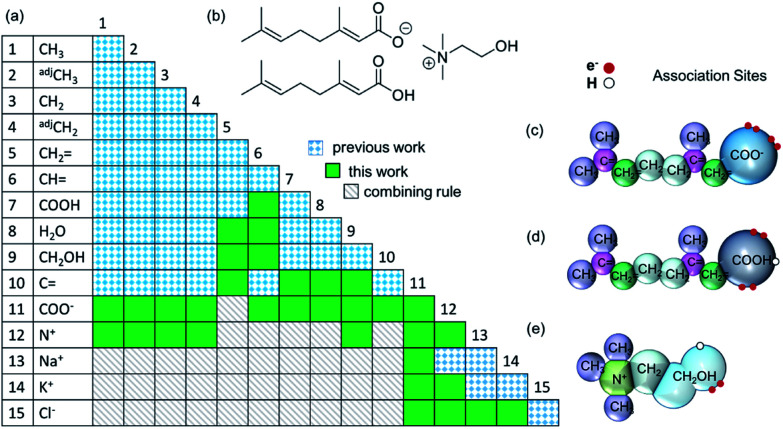
Fig. 1. (a) Group-interaction matrix, (b) molecular structure of choline geranate and geranic acid (CAGE). Graphical representations of the SAFT-γ Mie molecular decomposition for: (c) geranate; (d) geranic acid; and (e) choline.

As discussed in the Methods section, each functional group k is characterised by a fused spherical segment or, for larger groups such as CH₂OH, by a number 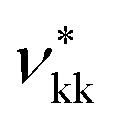of identical fused segments. The overlap of the different segments is taken into account by using the shape factor S_kk, which determines how much each segment contributes to the overall molecular properties. The matrix of functional groups and interactions required to characterise the mixtures of interest are summarised in Fig. 1(a). A number of the group parameters have been characterised in earlier work.¹⁸ In the current paper we expand the group-interaction matrix by estimating the interaction parameters needed to model CAGE; these are summarised in Tables 2–4.

Like group parameters for use within the SAFT-γ Mie group-contribution approach for the compounds considered in our study.

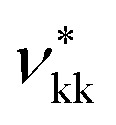
Group k		S kk	σ kk/Å	σ Born /Å	λ r	λ a	(εkk/kB)/K	N ST,k	n H,k	n e1,k	n e2,k	Ref.
CH3	1	0.57255	4.0773	—	15.050	6.0000	256.77	—	—	—	—	17
adjCH3	1	0.57255	4.0773	—	15.050	6.0000	256.77	—	—	—	—	This work
CH2	1	0.22932	4.8801	—	19.871	6.0000	473.39	—	—	—	—	17
adjCH2	1	0.22932	4.8801	—	19.871	6.0000	473.39	—	—	—	—	This work
CH2	1	0.44890	4.3175	—	20.271	6.0000	300.90	—	—	—	—	18
CH	1	0.20040	4.7488	—	15.974	6.0000	952.54	—	—	—	—	18
COOH	1	0.55593	4.3331	—	8.0000	6.0000	405.78	3	1	2	3	18
H2O	1	1.00000	3.0063	—	17.020	6.0000	266.68	2	2	2	—	68
CH2OH	2	0.58538	3.4054	—	22.699	6.0000	407.22	2	1	2	—	19
C	1	0.15330	4.0330	—	8.0000	6.0000	1500.0	—	—	—	—	69
COO−	1	0.55593	4.3331	4.6364	8.0000	6.0000	21.264	1	—	4	—	This work
N+	1	0.15069	3.0755	3.2908	8.8971	6.0000	62.971	1	1	—	—	This work
Na+	1	1.00000	2.3200	3.3600	12.000	6.0000	31.711	0				20
K+	1	1.00000	3.0400	4.3440	12.000	6.0000	90.097	0				20
Cl−	1	1.00000	3.3400	3.8740	12.000	6.0000	113.77	0				20

Unlike dispersion interaction energies (ε_kl/k_B)/K and repulsive exponents λ^r_kl for use within the SAFT-γ Mie group-contribution approach. CR indicates a combining rule is used to determine the value of the corresponding parameter. The unlike dispersion interactions indicated with CR are calculated using eqn (7) for uncharged groups and eqn (10) for charged groups. The combining rule used to determine the value of λ^r_kl is given in eqn (6). The unlike group diameters σ_kl are obtained using the combining rule given in eqn (5) in all cases.

Group k	Group l	(εkk/kB)/K	λ r	Ref.	Group k	Group l	(εkk/kB)/K	λ r	Ref.
CH3/adjCH3	CH3/adjCH3	256.77	15.05	17	CH	Cl−	CR	CR	This work
CH3/adjCH3	CH2/adjCH2	350.77	CR	17	COOH	COOH	405.78	8.0000	18
CH3/adjCH3	CH2	333.48	CR	18	COOH	H2O	289.76	CR	19
CH3/adjCH3	CH	252.41	CR	18	COOH	CH2OH	656.80	CR	19
CH3/adjCH3	COOH	255.99	CR	18	COOH	C	609.87	CR	This work
CH3/adjCH3	H2O	358.18	100	19	COOH	COO−	405.78	8	This work
CH3/adjCH3	CH2OH	333.20	CR	19	COOH	N+	CR	CR	This work
CH3/adjCH3	C	281.40	CR	69	COOH	Na+	CR	CR	This work
CH3	COO−	255.99	CR	This work	COOH	K+	CR	CR	This work
adjCH3	COO−	509.37	CR	This work	COOH	Cl−	CR	CR	This work
CH3/adjCH3	N+	462.18	CR	This work	H2O	H2O	266.68	17.020	68
CH3/adjCH3	Na+	CR	CR	This work	H2O	CH2OH	353.37	CR	19
CH3/adjCH3	K+	CR	CR	This work	H2O	C	310.91	8	This work
CH3/adjCH3	Cl−	CR	CR	This work	H2O	COO−	171.61	CR	This work
CH2/adjCH2	CH2/adjCH2	473.39	19.871	17	H2O	N+	1481.3	21.217	This work
CH2/adjCH2	CH2	386.80	CR	18	H2O	Na+	539.68	CR	20
CH2/adjCH2	CH	459.40	CR	18	H2O	K+	376.25	CR	20
CH2/adjCH2	COOH	413.74	CR	18	H2O	Cl−	95.406	CR	20
CH2/adjCH2	H2O	423.63	100	19	CH2OH	CH2OH	407.22	22.699	19
CH2/adjCH2	CH2OH	423.17	CR	19	CH2OH	C	799.66	CR	This work
CH2/adjCH2	C	286.58	CR	69	CH2OH	COO−	656.80	CR	This work
CH2	COO−	413.74	CR	This work	CH2OH	N+	440.99	CR	This work
adjCH3	COO−	780.24	CR	This work	CH2OH	Na+	CR	CR	This work
CH2/adjCH2	N+	348.30	CR	This work	CH2OH	K+	CR	CR	This work
CH2/adjCH2	Na+	CR	CR	This work	CH2OH	Cl−	CR	CR	This work
CH2/adjCH2	K+	CR	CR	This work	C	C	1500	8.0000	69
CH2/adjCH2	Cl−	CR	CR	This work	C	COO−	609.87	CR	This work
CH2	CH2	300.90	20.271	18	C	N+	CR	CR	This work
CH2	CH	275.75	CR	18	C	Na+	CR	CR	This work
CH2	COOH	387.25	94.463	This work	C	K+	CR	CR	This work
CH2	H2O	375.51	CR	This work	C	Cl−	CR	CR	This work
CH2	CH2OH	203.76	CR	This work	COO−	COO−	405.78	8	This work
CH2	C	CR	CR	This work	COO−	N+	24.280	CR	This work
CH2	COO−	CR	CR	This work	COO−	Na+	9.9125	CR	This work
CH2	N+	CR	CR	This work	COO−	K+	23.999	CR	This work
CH2	Na+	CR	CR	This work	COO−	Cl−	21.265	CR	This work
CH2	K+	CR	CR	This work	N+	N+	394.86	9.9448	This work
CH2	Cl−	CR	CR	This work	N+	Na+	CR	CR	This work
CH	CH2	952.54	15.974	18	N+	K+	CR	CR	This work
CH	COOH	453.13	CR	This work	N+	Cl−	61.989	CR	This work
CH	H2O	332.21	17.309	This work	Na+	Na+	31.711	12	20
CH	CH2OH	414.91	CR	This work	Na+	K+	CR	CR	This work
CH	C	1195.3	CR	This work	Na+	Cl−	27.938	CR	20
CH	COO−	453.13	CR	This work	K+	K+	90.097	12	This work
CH	N+	CR	CR	This work	K+	Cl−	61.010	CR	20
CH	Na+	CR	CR	This work	Cl−	Cl−	113.77	12	20
CH	K+	CR	CR	This work

Association energy ε^HB_ab,kl and bonding volume K^HB_ab,kl parameters for use within the SAFT-γ Mie group-contribution approach. For groups with several site types, the interactions are symmetrical, e.g., ε^HB_ab,kl = ε^HB_ba,kl. Interactions not reported here are set to zero.

Group k	Site of group k	Group l	Site a of group l	(εHBab,kl/kB)/K	K HB /Å3	Ref.
COOH	H	COOH	H	6427.9	0.80620	18
COOH	e1	H2O	H	1451.8	280.89	19
COOH	e2	H2O	H	1252.6	150.98	19
COOH	H	H2O	e1	2567.7	270.09	19
COOH	e1	CH2OH	H	1015.5	21.827	19
COOH	e2	CH2OH	H	547.40	53.150	19
COOH	H	CH2OH	e1	524.00	14.017	19
H2O	e1	H2O	H	1985.4	101.69	68
H2O	e1	CH2OH	H	621.68	425.00	19
H2O	H	CH2OH	e1	2153.2	147.40	19
H2O	H	COO−	e1	802.20	52.560	This work
H2O	e1	N+	H	2783.7	15.536	This work
CH2OH	e1	CH2OH	H	2097.9	62.310	19
CH2OH	H	N+	e1	1247.2	286.83	This work

As has already been mentioned, the characterisation of the group-interaction parameters is done in a successive manner. We proceed to analyse first the performance of the model in predicting the properties of pure geranic acid, follow with aqueous geranic acid mixtures, aqueous carboxylate salts solutions, and finally choline chloride and aqueous CAGE solutions.

3.1. Geranic acid

The group-interaction parameters required to model geranic acid are estimated using experimental phase-equilibrium data of pure compounds (e.g., n-alkanes, n-alkenes, branched alkenes) and mixtures (e.g., branched alkenes and carboxylic acids), as shown below.

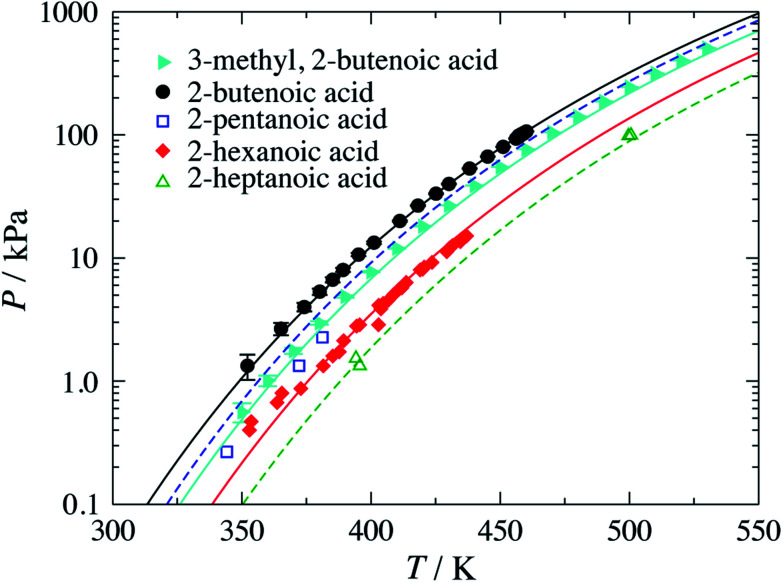
Pure-component experimental data^32–35 are used to characterise the unlike interactions between the carboxylic group COOH and the alkene groups (either linear CH , or branched C ). The experimental vapour–pressure data for pure branched and unsaturated carboxylic acids used to perform the parameter estimations, and to assess the predictive capability of the resulting models, are shown in Fig. 2. Although most of the group-interaction parameters needed to calculate the vapour pressure of the compounds presented in the figure are not optimised for these systems, the model is found to provide a good description of the experimental data.

Fig. 2. Vapour pressure of branched and unsaturated carboxylic acids. The symbols correspond to the experimental data for 3-methyl-2-butenoic acid,³² 2-butenoic acid,³³ 2-pentenoic acid,³⁴ 2-hexenoic acid³² and 2-heptenoic acid.³⁵ The filled symbols indicate experimental data used in the parameter estimation, while the open symbols are the data used to determine the adequacy of the theoretical description. The continuous curves correspond to calculations and predictions using SAFT-γ Mie group-contribution approach.

A summary of the % AAD values for the vapour pressure and saturated-liquid density for the branched alkenes and unsaturated carboxylic acids considered in our current work is presented in Table 5. The reported values for the vapour pressure and saturated-liquid density, % AAD P_vap = 7.96% and % AAD ρ_sat = 3.94%, are slightly higher than the typical % AAD obtained for alkanes and carboxylic acids.^19,36 We note that both the CH and C are very small groups with shape factors of 0.20037 and 0.15330, respectively. The small groups thus make a smaller contribution to the thermophysical properties of the solution, and are thus more difficult to characterise. In the case of 2-pentenoic acid we find an especially large deviation of 34.5%; while this may suggest that further effort is required to refine the group-interaction parameters, we also highlight a large error reported in the experimental data source.³⁴

Percentage average absolute deviations (% AAD) for the vapour pressure P_vap and saturated-liquid density ρ_sat considered in the estimation procedure for the development of the SAFT-γ Mie model parameters and the assessment of the performance of the model for pure compounds of interest here. N_P and N_ρ are the number of data points of P_vap and ρ_sat, respectively. The references to the experimental data are denoted in each case.

Compound	T/K	N P	% AAD Pvap	Ref.	T/K	N ρ	% AAD ρsat	Ref.
2-Butenoic acid	352–460	23	2.67	33
2-Pentenoic acid	350–450	11	34.5	34
2-Hexenoic acid	352–437	30	11.2	32
3-Methyl-2-butenoic acid	350–530	19	20.7	32	350–530	19	2.18	32
2-Methyl-1-butene	274–413	30	3.63	34	183–408	24	4.37	34
2-Methyl-1,3-butadiene	215–328	58	1.59	34	193–433	14	5.06	34
Average			7.96				3.94

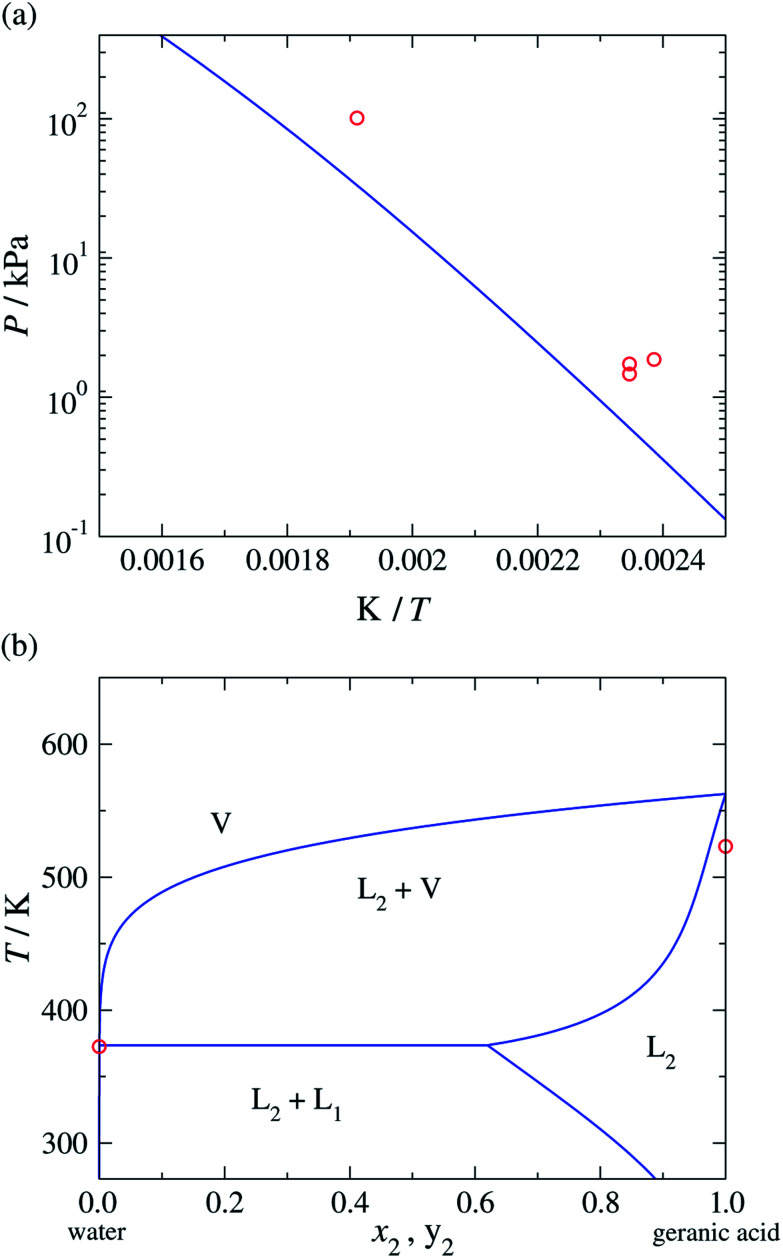
Once these groups have been characterised, the SAFT-γ Mie approach can be used to predict the vapour pressure of geranic acid. In comparisons with the available experimental data^37–39 (see Fig. 3(a)), we find an over-prediction of the vapour pressure of geranic acid, with an % AAD= 67.4%. Although this value is rather large, we note the scarcity of data, the discrepancies between the various experimental sources, and the small values of the pressures, with most data points two orders of magnitude below atmospheric pressure.

Fig. 3. (a) Vapour pressure of geranic acid. (b) Temperature-composition phase diagram of water (1) + geranic acid (2) at a constant pressure of P = 101.325 kPa. The red symbols correspond to the experimental data^37–39 and the continuous curves to the predictions obtained with the SAFT-γ Mie group-contribution approach.

Following the decomposition of geranic acid into the appropriate functional groups and the estimation of the relevant group-interaction parameters, we proceed to develop the interaction parameters between the functional groups of geranic acid and water. Experimental vapour–liquid equilibrium (VLE) and liquid–liquid equilibrium (LLE) data of binary mixtures of n-alkenes and water are used to determine the unlike dispersion energy and repulsive-range parameters between H₂O and the three unsaturated groups: CH₂ , CH and C . More specifically, VLE data of propylene + water and 2-methyl-1,3-butadiene + water mixtures and LLE data of 1-butene + water mixtures are used.⁴⁰ Despite the limited experimental data available for these systems, the SAFT-γ Mie calculations are found to be in relatively good agreement with the experimental data: we find % AADs for all the LLE and VLE data of 5.51% and 5.72%, respectively (see Tables 6 and 7). Once all of the group interactions are characterised, the approach can be used to model a range of thermophysical properties of geranic acid and water mixtures at different thermodynamic states, for broad ranges of compositions, temperatures and pressures. The predicted temperature-composition binary phase diagram of the mixture at a constant pressure P = 101.325 kPa is shown in Fig. 3(b), where regions of vapour–liquid and liquid–liquid equilibria can be seen. As in the case of pure geranic acid, there is a lack of experimental data for the mixture, which makes the analysis of the adequacy of our model in reproducing the experimental data difficult.

Percentage average absolute deviations (% AAD) for the vapour–liquid equilibrium data considered in the estimation procedure for the development of the SAFT-γ Mie model parameters and the assessment of the performance of the model. Experimental data for the bubble pressure are considered in the estimation procedure. The dew pressure and temperature are predicted. N_P indicates the number of data points used.

Mixture	T/K	N P	% AAD PBubble	Ref.
Propylene + water	311–344	15	6.05	70
1-Propene + 1-propanol	283–313	41	9.28	71

Mixture	T/K	N P	% AAD PDew	Ref.
Propylene + water	311–344	15	7.25	70

Mixture	P/kPa	N P	% AAD T	Ref.
2-Methyl-1,3-butadiene + 1-butanol	101.330	6	0.28	40

Percentage average absolute deviations (% AAD) from the experimental liquid–liquid equilibria (LLE) data considered in the estimation procedure for the development of the SAFT-γ Mie model and assessment of the model. N_P indicates the number of data points used.

Mixture	T/K	N P	% AAD xbutene rich phase	% AAD xwater rich phase	Ref.
1-Butene + water	311–411	40	16.60	0.61	72
2-Methyl-1,3-butadiene + water	293.15	1	4.75	0.096	34

3.2. Aqueous solutions of carboxylate salts

The modelling of aqueous carboxylate salt solutions requires the development of the anionic carboxylate functional group, COO⁻, and its interactions with other groups, including H₂O. We have characterised these interactions by considering aqueous solutions of sodium carboxylate salts, R–COO⁻Na⁺, of various chain lengths (where R is CH₃–(CH₂)_n with 0 ≤ n ≤ 4). We treat the salts as strong electrolytes, fully dissociated in aqueous solutions, neglecting the formation of ion pairs between the carboxylate anions and the alkali metal cations. This is consistent with experimental evidence, where the strength of ion pairing has been reported to be very weak,⁴³ for the shorter alkyl carboxylate anions, namely formate and acetate salts.^44–46 We note, however, that the short-chain salts exhibit typical 1 : 1 electrolyte behaviour, whereas salts with chains longer than C₄ exhibit increasingly atypical behaviour due to the aggregation of the anion in solution,^47–50 with critical micellar concentrations reported to decrease as the alkyl chain length is increased.⁴⁷ It is important to note that in its current formulation the SAFT-γ Mie approach does not account for the formation of micelles.

The group interactions needed to model carboxylate salt solutions are estimated using experimental osmotic coefficient data^41,42 of dilute and moderately concentrated salt solutions up to m_{R-COO⁻Na⁺} ≤ 1.0 mol kg⁻¹ for the shorter alkylates (CH₃COONa, C₂H₅COONa and C₃H₇COONa) and up to m_{R-COO⁻Na⁺} ≤ 0.7 mol kg⁻¹ for larger carboxylate salts (C₄H₉COONa and C₅H₁₁COONa).

The SAFT-γ Mie model parameters for the COO⁻ group are based on those previously determined for the uncharged carboxylic group (COOH), assuming that the overall shape of the COOH functional group does not change appreciably with the loss of a proton: identical values are used for the number of spherical segments 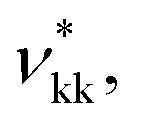the shape factor S_kk, and the segment diameter σ_kk, as well as for the exponents (λ^r_kk, λ^a_kk) of the Mie potential to model COO⁻ as to model COOH. The diameter required for the calculation of the Born term of the COO⁻ group is obtained following the method proposed by Rashin and Honig;²⁹i.e., 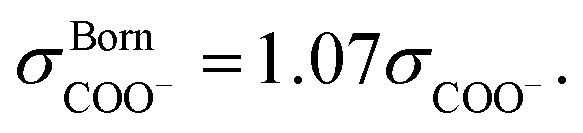The dispersion energy ε_kk between ions is calculated using the polarisability α₀ and the ionisation potential I (electron affinity) of the COO⁻ functional group by applying eqn (10), as for previous models developed for ionic groups.²⁰ The values used for the polarisability and the electron affinity are reported in Table 1. The unlike dispersion energy for the COO⁻–Na⁺ pair is also obtained with eqn (10), using the experimental values of α₀ and I shown in Table 1, and the unlike interactions between H₂O and Na⁺ are take from ref. 20. The unlike dispersion energy parameters between COO⁻ and the alkyl groups are given the same values as those between COOH and the alkyl groups. In terms of the interaction of the COO⁻ group with H₂O, the unlike diameter is obtained using the standard combining rule presented eqn (5) (in effect resulting in the same value as σ_COOH,H2O between the COOH group and H₂O). The only interactions which are refined relate to the unlike dispersion and association interactions between COO⁻ and H₂O. Four association sites of type e, corresponding to the lone pairs of electrons of the oxygen atoms in the COO⁻ group are considered. This is consistent with the fact that this anion is reported to have a symmetrical structure, with the alkali cations showing no significant tendency to interact preferentially with any one of the oxygens atoms.⁴³ This is in contrast to the association interactions used to represent the COOH group, where the two oxygen atoms are clearly distinguishable, resulting in two distinct peaks in the photoelectron spectrum.⁵¹ Self-association between COO⁻ ions is not considered. The SAFT-γ Mie model parameters for COO⁻ are given in Table 2.

Values for the electron affinity I_k and the polarisability α_0,k for the ions considered in our work, taken from ref. 65–67 and used in eqn (10).

Group k	COO−	Cl−	N+	Na+	K+
I k/eV	3.4700	3.6127	14.534	47.286	31.630
α 0,k/(10−24 cm3)	4.2042	3.6600	1.1000	0.1790	0.8300

As with the previous systems, the development of the interaction parameters follows a stepwise procedure. The H₂O–COO⁻ unlike interaction parameters (ε_kl, ε^HB_kl and K^HB_kl) are optimised using osmotic coefficient data of aqueous solutions of sodium butanoate for concentrations up to m_{R-COO⁻Na⁺} ≤ 1 mol kg⁻¹ and of sodium pentanoate and hexanoate salts for concentrations up to m_{R-COO⁻Na⁺} ≤ 0.7 mol kg⁻¹. Carboxylate salts with shorter alkyl chains than butanoate are not considered in the parameter estimation procedure as the COO⁻ group is expected to have a large polarising effect on the neighbouring alkyl groups in such compounds. We note that similar assumptions were made in the development of the COOH group,³⁶ which was characterised using carboxylic acids with chain lengths larger than C₄.

Nevertheless, it is important to be able to model shorter chain-length carboxylates, and we develop tailored models specifically for these compounds. In order to take into account the polarization effect in the shorter-chained carboxylic acids and carboxylate salts, second-order adjacent groups ^adjCH₂ and ^adjCH₃ are introduced to model the acetates and propanoates. The same like- and unlike-interaction parameters are employed for these adjacent functional groups as for the regular CH₂ and CH₃ alkyl groups, but different ^adjCH₂–COO⁻ and ^adjCH₃–COO⁻ unlike parameters between the adjacent alkyl groups and the carboxylate group are determined; these are estimated from an additional parameter estimation procedure using osmotic coefficient data of aqueous sodium propanoate and sodium acetate solutions at standard conditions for concentrations up to m_{R-COO⁻Na⁺} ≤ 1.0 mol kg⁻¹. Thus, when modelling a carboxylate CH₃–(CH₂)_n–COO⁻, one uses the ^adjCH₃–COO⁻ and ^adjCH₂–COO⁻ unlike interactions for n = 0, 1, 2 and the CH₃–COO⁻ and CH₂–COO⁻ interactions for n > 2. All the SAFT-γ Mie group parameters used in our current work are summarised in Tables 2–4.

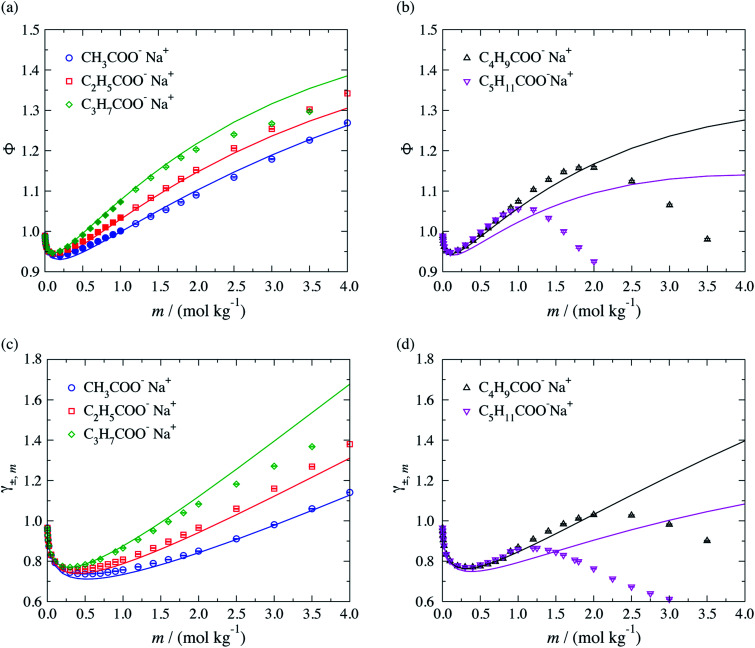
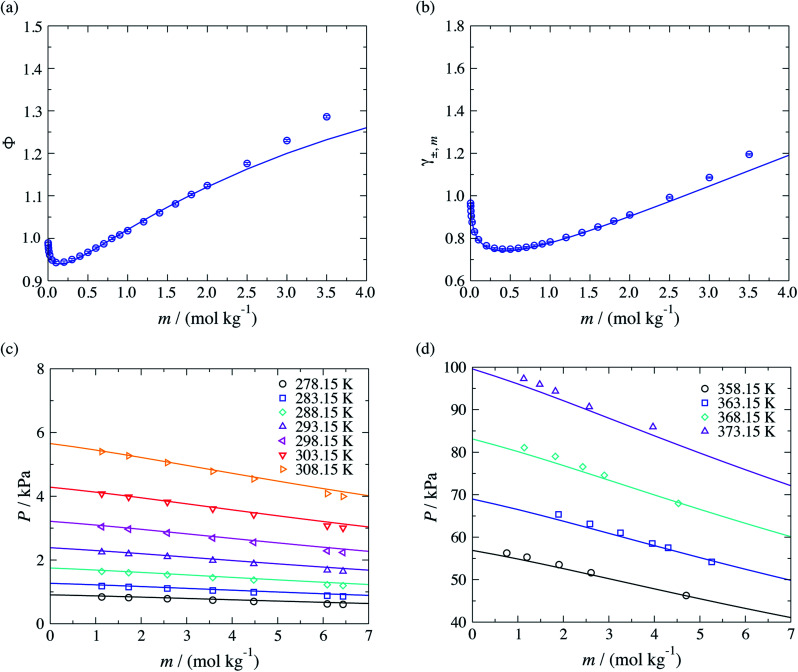
The performance of the SAFT-γ Mie group-contribution approach for aqueous solutions of sodium carboxylate salts is assessed by predicting the thermodynamic properties of a number of systems at several thermodynamic states not considered in the parameter estimation procedure. The osmotic coefficient, the mean ionic activity coefficient, liquid-phase density and vapour pressure beyond the concentration range included in the parameter estimation are predicted and compared to experimental data in Fig. 4. We note that experimental data for both the density and the vapour pressure are scarce for solutions of carboxylate anions larger than CH₃COO⁻. The activity and osmotic coefficients of dilute solutions exhibit a concentration dependence which is typical of that for strong electrolyte solutions and the magnitude of both is seen to increase with increasing chain length of the salt. The theoretical predictions are seen to be in good overall agreement with the experimental data available in the lower range of concentrations, both in terms of the activity and the osmotic coefficients. The concentration dependence of the activity and osmotic coefficients for the larger chain carboxylate salts (≥C₄) exhibit a change in slope from positive to negative, with a maximum at a specific concentration (cf.Fig. 4(b) and (d)), which is related to micelle formation.^47–50 The current SAFT-γ approach does not account for these aggregates, and as a result the predictions are seen to deviate from the data at higher concentrations for the butanoate and pentanoate salts.

Fig. 4. Concentration dependence of (a and b) the osmotic coefficient Φ and (c and d) mean ionic activity coefficient γ_±,m for aqueous sodium carboxylate salts of different chain lengths at a temperature of T = 298 K and pressure of P = 101.325 kPa. The continuous curves are obtained using the SAFT-γ Mie group-contribution approach. The filled symbols represent the experimental data^41,42 considered for the parameter estimation while the open symbols are used to assess the adequacy of the theoretical prediction. The different symbols correspond to different compounds as specified in the legend.

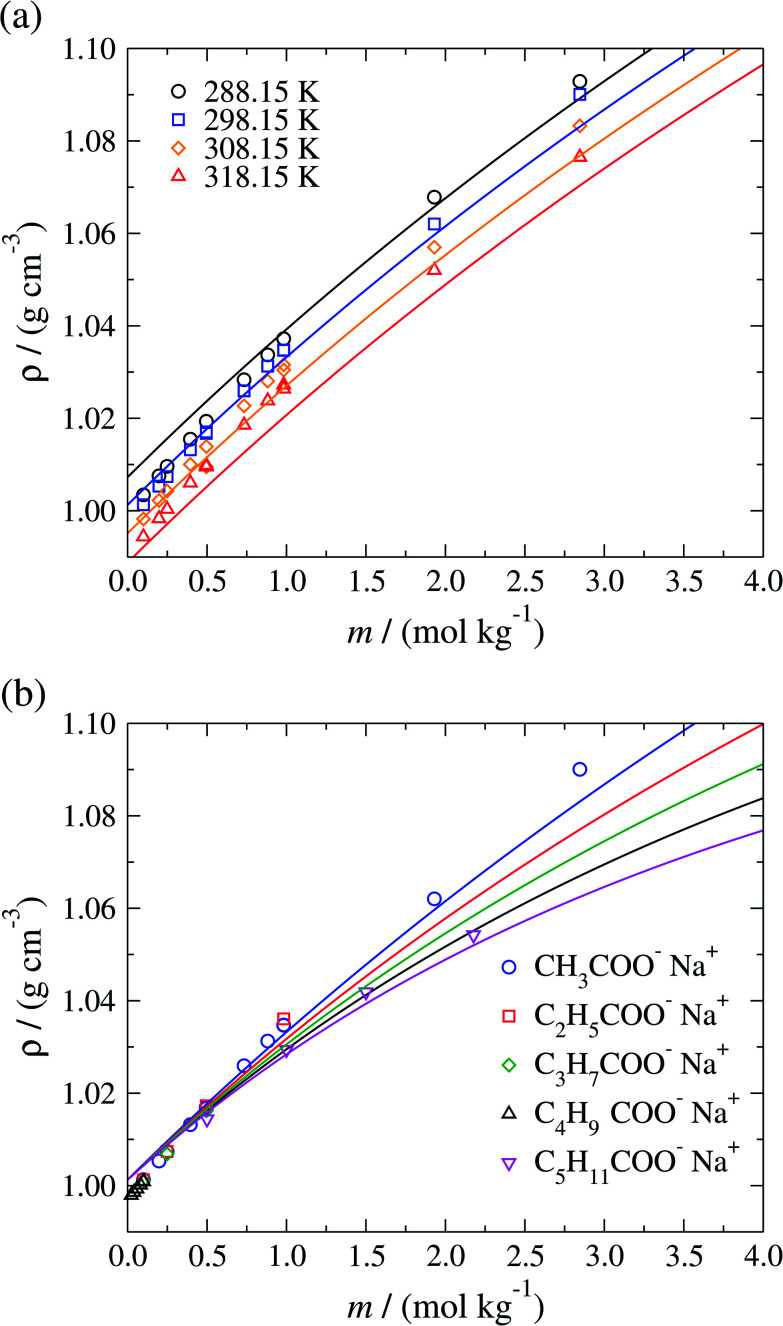
The isobaric liquid density ρ of aqueous sodium-carboxylate solutions is displayed in Fig. 5 as a function of the concentration for a temperature range of 288.15–318.15 K. The SAFT-γ Mie predictions are seen to be in good overall agreement with the available experimental data, with densities that increase with increasing salt concentration and decrease with increasing temperature. In Fig. 5(b) the model is seen to reproduce the experimental decrease in liquid density with increasing chain length of the carboxylate anions. The model overestimates the available liquid-phase density data^52–59 of sodium carboxylate aqueous solutions at low (m_{R-COO⁻Na⁺} < 0.75 mol kg⁻¹) concentration (as a consequence of the overestimation of the density of pure water at the conditions considered), and underestimates the density at high concentrations (m_{R-COO⁻Na⁺} ≥ 0.75 mol kg⁻¹).

Fig. 5. Concentration dependence of the liquid-phase density ρ of (a) aqueous sodium acetate solutions at a pressure of P = 101.325 kPa over the temperature range 288.15–318.15 K, and (b) of different aqueous sodium carboxylate salt solutions at standard conditions, namely P = 101.325 kPa and T = 298.15 K for several carboxylate chain lengths. The continuous curves correspond to predictions using the SAFT-γ Mie group-contribution approach and the symbols to experimental data.^52–59 The different symbols correspond to different conditions and compounds as specified in the legends.

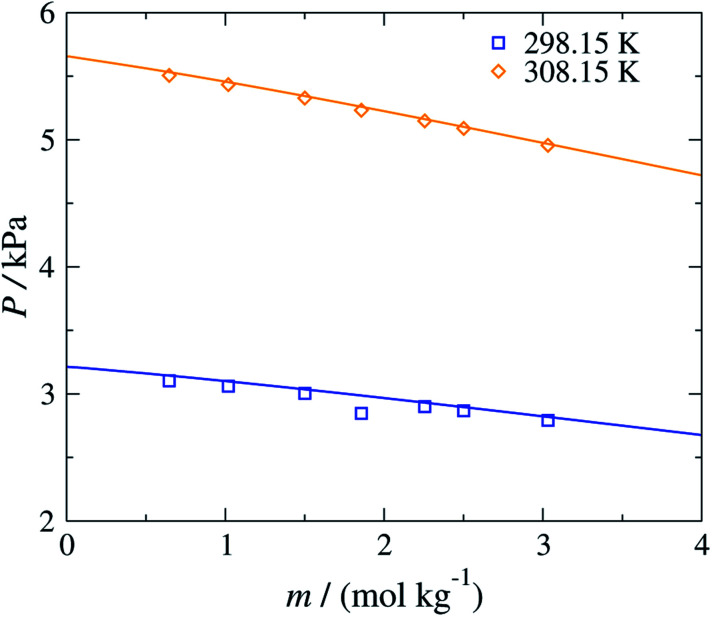
The versatility of the SAFT-γ Mie group-contribution approach is further illustrated in Fig. 6, where the concentration dependence of the vapour pressure of aqueous solutions of sodium acetate at 298.15 K and 308.15 K is shown. The SAFT-γ Mie theoretical predictions can be seen to reproduce the experimental results with quantitative accuracy. It is interesting to note that even though the model parameters are estimated from osmotic coefficient data for aqueous solutions of sodium carboxylate at T = 298.15 K and P = 101.325 kPa and only for a low range of concentrations, the other properties can be predicted accurately across a broad range of thermodynamic states.

Fig. 6. Concentration dependence of the vapour pressure P of aqueous sodium acetate solutions at 298.15 and 308.15 K. The continuous curves are obtained using the SAFT-γ Mie group-contribution approach. The symbols represents the experimental data.⁶⁰ The different symbols correspond to different conditions as specified in the legend.

Moreover, the models developed here can also be used to study aqueous solutions of potassium carboxylate. We now predict the osmotic and activity coefficients and vapour pressures of potassium acetate aqueous solutions. This test allows us to assess the transferability of the parameters that characterise the COO⁻–H₂O interactions, which are of key importance in representing the target CAGE mixture. As with other ions, the COO⁻–K⁺ unlike ion–ion dispersion energy is obtained with eqn (10), using the experimental values of α₀ and I given in Table 1, and the unlike interactions between H₂O and K⁺ are taken from ref. 20. The concentration dependence of the osmotic and activity coefficient of several aqueous solutions of potassium acetate at standard conditions are shown in Fig. 7, where the model is seen to provide a good description of the experimental data. A small underestimation of the data for salt concentration higher than m_{R-COO⁻Na⁺} ≥ 2.5 mol kg⁻¹ is noted, which may be related to ion aggregation and ion-pairing, a feature not considered in our current model. A very satisfactory representation of the vapour pressure for these systems over a broad range of temperatures can be seen Fig. 7(c) and (d).

Fig. 7. Prediction of thermophysical properties of aqueous solutions of potassium acetate for different thermodynamic states. Concentration dependence of (a) the osmotic coefficient Φ and (b) mean ionic activity coefficient γ_±,m at a temperature of T = 298 K and a pressure of P = 101.325 kPa, and concentration dependence (c) of the vapour pressure over the temperature range 278.15–303.15 K and (d) of the vapour pressure over the temperature range 358.15–373.15 K. The continuous curves correspond to the SAFT-γ Mie group-contribution approach. The symbols represent the experimental data for osmotic and activity coefficients,⁴¹ and the vapour pressures.^61,62 The different symbols corresponds to different conditions as specified in the legend.

We emphasise that this excellent agreement between the thermophysical properties predicted for a wide range of thermodynamic conditions and the experimental data is achieved using a unique set of transferable intermolecular parameters between the carboxylate group COO⁻ and H₂O for all the aqueous carboxylate salt solutions considered. The SAFT-γ Mie model developed for these systems is shown to be transferable and robust. The performance of the model will be further assessed for choline chloride and CAGE in the following sections.

3.3. Aqueous solutions of choline choride

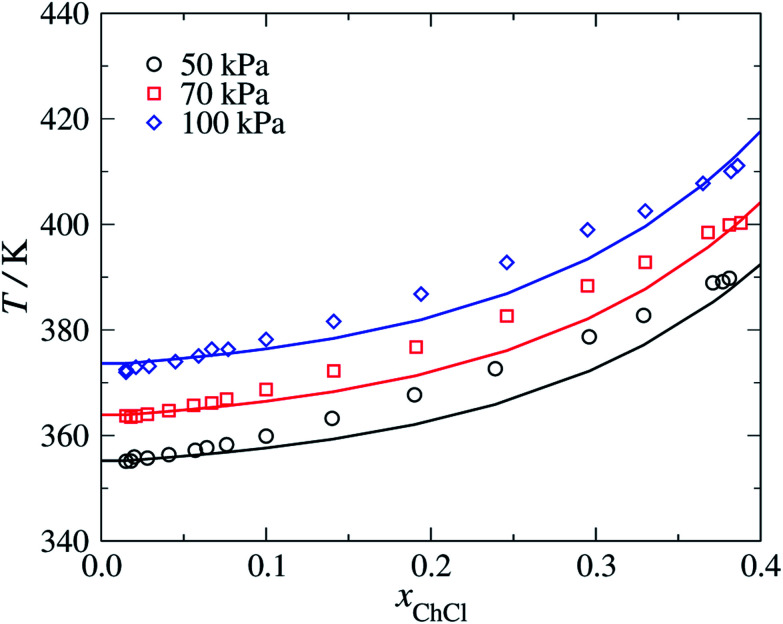
We model choline chloride as fully dissociated in water. An N⁺ group is used in the cation, which is characterised using parameters based on those of the uncharged N group present in triethanolamine.⁶³ The unlike dispersion energy parameters between N⁺ and the alkyl groups and between N⁺ and CH₂OH are given the same values as those between N and the alkyl groups and between N and CH₂OH, respectively.⁶³ The COO⁻–Cl⁻ unlike dispersion energy is obtained with eqn (10), using the experimental values of α₀ and I given in Table 1, and the unlike interactions between H₂O and Cl⁻ are taken from ref. 20. The parameters summarised in Tables 2–4 are used to predict the isobaric temperature-composition vapour–liquid equilibria of aqueous solutions of choline chloride.⁶⁴ The resulting SAFT-γ Mie predictions are shown in Fig. 8 as a function of the salt concentration for various pressures. It is encouraging to see that although a group-contribution approach is used in the development of the model of choline chloride, with all the interactions transferred from group interactions characterised using other compounds and thermodynamic states, or through combining rules, our calculations provide a description of the vapour–liquid equilibria which are in close agreement with the available experimental data.⁶⁴

Fig. 8. Isobaric vapour–liquid equilibria for aqueous solution of choline chloride (ChCl) at pressures of P = 50, 70 and 100 kPa. The continuous curves correspond to SAFT-γ Mie predictions and the symbols to the experimental data.⁶⁴.

3.4. Aqueous mixture of choline, geranate and geranic acid (CAGE)

In addition to the groups characterised thus far, the description of the thermodynamic properties of aqueous solutions of CAGE requires the determination of the interactions between the CH₂OH group and the C and CH groups; the unlike dispersion energies between these groups are given in Table 2. In the characterisation of these interactions we have used experimental vapour–liquid equilibrium data of 1-propene + 1-propanol and 2-methyl-1,3-butadiene + 1-butanol binary mixtures (see Table 6). Having characterised these group interactions it is possible to carry out predictive calculations of the thermodynamic properties of the CAGE + water mixture of interest with the SAFT-γ Mie group-contribution approach. CAGE is modelled as a 1 : 1 : 1 mole ratio mixture of choline : geranate : geranic acid, and the calculated density of the mixtures is used to convert from mole fraction to molarity in order for direct comparisons with the experimental data.

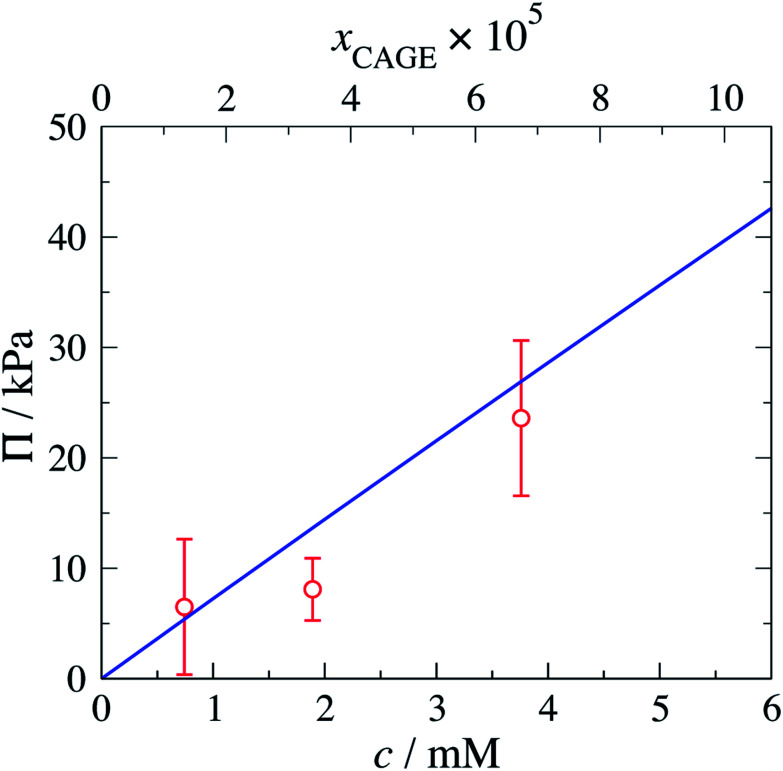
The predicted osmotic pressure for CAGE + water mixtures as a function of concentration is shown in Fig. 9 together with the experimental values obtained in this work. The measured data and corresponding SAFT-γ Mie predictions can also be found in Table 8. We note the relatively larger standard deviation reported for the lowest concentration in Table 8 is caused by one of the three repeated values at this concentration returning a value of zero. The zero reading may have been due to poor sampling or to a cancellation of thermodynamic effects. The osmometer directly compares the dew point depression of the CAGE + water sample with an internal water reference. It is known that CAGE + water mixtures undergo structural re-arrangements. If these re-arrangements were associated with an exothermic change, the energy released may have increased the temperature and thus cancelled the effect of dew-point depression, resulting in an overall reading value of zero. The instrument thermocouple has a resolution of 0.00031 °C.

Fig. 9. Concentration dependence of the osmotic pressure for aqueous mixtures of CAGE at a temperature of T = 293.15 K and pressure of P = 103.3515 kPa. The top axis indicates the mole fractions of CAGE corresponding to the concentrations on the bottom axis. The continuous curve corresponds to the predictions with the SAFT-γ Mie group-contribution approach. The symbols represent the experimental data obtained in the current work.

Measured and predicted osmotic pressure for aqueous mixture of CAGE, Π^exp_CAGE and Π^SAFT_CAGE, respectively, at the specified concentrations, both concentration c and mole fraction of CAGE, x_CAGE. % AAD is the percentage average absolute deviation.

x CAGE × 105	c/(103× mol L−1)	ΠexpCAGE/kPa	ΠSAFTCAGE/kPa	% AAD
1.33	0.74278	6.50 ± 6.1340	5.3867	17.118
3.39	1.8907	8.10 ± 2.8140	13.629	67.759
6.75	3.7589	23.6 ± 7.0357	26.888	14.125

In terms of the agreement of the SAFT-γ Mie calculations and the experimental data we emphasise that the experimental data presented in this section are not considered in the development of the model for these solutions. The good agreement between the predictions and the measured data highlights the capability and robustness of the models developed here.

4. Conclusions

The SAFT-γ Mie group-contribution approach is used to predict the osmotic pressure of mixture involving choline, geranate, and geranic acid (CAGE) and the adequacy of the approach is assessed by comparison with new experimental measurements obtained as part of this work. A number of new SAFT-γ Mie groups and group interactions, including ionic groups, appropriate to model the system of interest are characterised using a variety of experimental phase-equilibrium and solution data for pure components and mixtures. The model is successively tested by carrying out predictive calculations for representative mixtures, conditions, and properties not used in the parameter development. The SAFT-γ predictions are shown to be in very good overall agreement with the experimental data for the systems tested. In particular we develop a model for aqueous solutions of carboxylate salts, assuming the charged species are fully dissociated in water and neglecting micelle formation. The model developed is found to be predictive and fully transferable to other carboxylate salts solutions at different thermodynamic conditions, up to concentrations where micellisation is expected. A model for choline chloride is also presented, considering the anion and cation as dissociating species in water. We further extend the set of functional groups in the SAFT-γ Mie approach introducing new groups, such as COO⁻ and N⁺. The resulting model is then used to predict the osmotic pressure of aqueous CAGE solutions, which is found in excellent agreement with experimental measurements. These encouraging results confirm the transferability and robustness of the SAFT-γ group-contribution approach for the prediction of thermodynamic properties of complex mixtures in general and highlights its promise for applications involving deep-eutectic solvent mixtures and ionic liquids in particular.

Data statement

Data underlying this article can be accessed on Zenodo at https://zenodo.org/record/3540689#.Xcv6WFf7Q2x, and used under the Creative Commons Attribution license.

Conflicts of interest

There are no conflicts to declare.