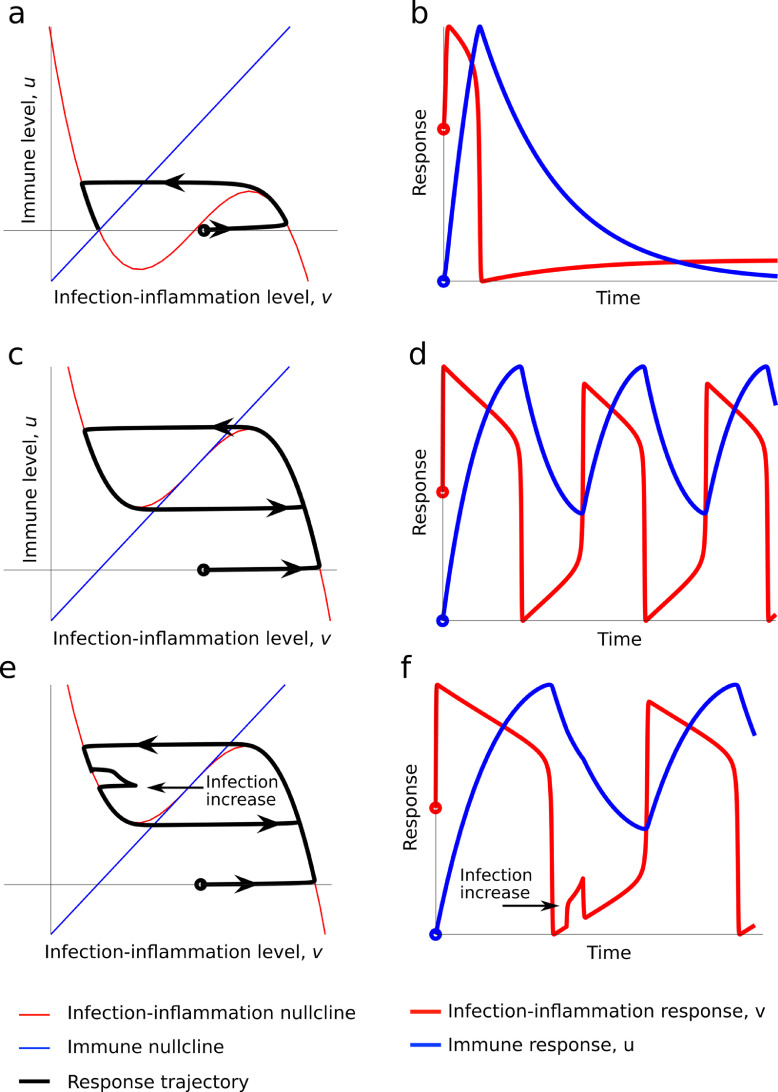
Figure 4.

Mathematical simulation of case scenarios for resolving, non-resolving and endotoxin tolerance-hypo-inflammation. Panels a and b: Resolving infection simulation. The left panel shows the “phase plane” plot of the solution trajectory in the (v,u) coordinates, which is the black line. The arrows on the black line represent the evolution of the solution and, we observe that when the black line terminates it does so at a point where the nullclines (red and blue lines) cross. The right panel represents the trajectories of the (t,v) (red line) and (t,u) (blue line) solutions, respectively. (v₀,u₀) = (1.1,0). Panels c and d show non-resolving infection simulation. By providing a constant source of infection, i.e. S > 0, we cause the u-nullcline to cut only the central branch of the v-nullcline and, therefore, results in an unresolved immune-infection response. To achieve this the infection source has been increased to S = 10. (v₀,u₀) = (1.1,0). Panels E and F show Endotoxin tolerance (hypo-inflammatory) simulation. Phase plane (left) and simulated trajectories (right) of Eqs. (1) and (2). In the right plot the red line illustrates the infection level whilst the blue represents the immune response. This is the same simulation as shown in panels c and d, except an additional constant infection source between the first and second oscillation. This is seen and the perturbation in the black and red lines in the left and right plots, respectively. The initial conditions are (v₀,u₀) = (1.1,0) and S = 10.