Skip to main content
PMC home page
RSC Advances logoLink to RSC Advances
. 2018 Jul 30;8(48):27081–27090. doi: 10.1039/c8ra03602k

Membrane partition of bis-(3-hydroxy-4-pyridinonato) zinc(ii) complexes revealed by molecular dynamics simulations†,‡

João T S Coimbra 1, Natércia F Brás 1, Pedro A Fernandes 1, Maria Rangel 2,✉, Maria J Ramos 1,✉
PMCID: PMC9083369  PMID: 35539964

Abstract

The class of 3-hydroxy-4-pyridinone ligands is widely known and valuable for biomedical and pharmaceutical purposes. Their chelating properties towards biologically-relevant transition metal ions highlight their potential biomedical utility. A set of 3-hydroxy-4-pyridinone Zn(ii) complexes at different concentrations was studied for their ability to interact with lipid phases. We employed umbrella sampling simulations to attain the potential-of-mean force for a set of ligands and one Zn(ii) complex, as these permeated a 1,2-dimyristoyl-sn-glycero-3-phosphocholine (DMPC) hydrated bilayer system. In addition, we used conventional molecular dynamics simulations to study the behavior of various Zn(ii) complexes in hydrated bilayer systems. This work discusses: (i) the partition of 3-hydroxy-4-pyridinone ligands to bilayer phases; (ii) self-aggregation in crowded environments of Zn(ii) complexes; and (iii) possible mechanisms for the membrane translocation of Zn(ii) complexes. We observed distinct interactions for the studied complexes, and distinct membrane partition coefficients (Kmem) depending on the considered ligand. The more hydrophobic ligand, 1-hexyl-3-hydroxy-2-methyl-4(1H)-pyridinone, partitioned more favorably to lipid phases (at least two orders of magnitude higher Kmem when compared to the other ligands), and the corresponding Zn(ii) complex was also prone to self-aggregation when an increased concentration of the complex was employed. We also observed that the inclusion of a coordinated water molecule in the parameterization of the Zn(ii) coordination sphere, as proposed in the available crystallographic structure of the complex, decreased the partition coefficient and membrane permeability for the tested complex.

The membrane partition of hydroxypyridinones and of zinc complexes explored by molecular dynamics.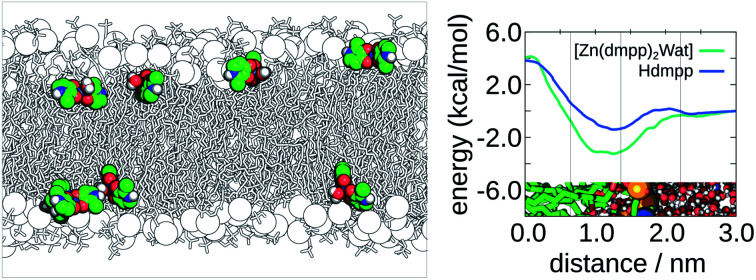graphic file with name c8ra03602k-ga.jpg

Introduction

The class of 3-hydroxy-4-pyridinone (3,4-HPO) ligands is widely known and valuable for biomedical, environmental and agricultural applications.1–3 Their value lies in the chelating properties they possess for distinct and biologically-relevant transition-metal ions, such as copper, zinc, and iron. Fig. 1 illustrates the chemical structure of a dataset of 3,4-HPO ligands that were studied in this work. The hydroxyl and ketone groups in the ring are responsible for the strong chelating properties associated with these compounds. An additional and very important characteristic of these ligands is the fact that they can incorporate different hydrophilic/lipophilic substituents with no significant alteration of the stability constants for the metal ions.4–7

Fig. 1. Molecular structure of the dataset of 3,4-HPO ligands and respective abbreviations.

Fig. 1

Open in a new tab

Currently, the compound 1,2-dimethyl-3-hydroxy-4-pyridinone (Hdmpp), commercially known as deferiprone, is successfully used in the treatment of iron overload disorders, such as β-thalassemia. Several other 3,4-HPO ligands have been pointed out as regulators of iron and copper homeostasis.7,8 Their role in zinc homeostasis has been also highlighted.8 Since zinc is an essential metal ion for most organisms, it could play a central part in several diagnostic and therapeutic purposes. Its administration seems to be beneficial in some specific situations, such as the use of Zn-citrate to prevent dental plaque formation, or the employment of zinc isotopes in radiopharmaceutical therapies. Interestingly, when complexed with citrate, several EDTA-derivatives, and 3,4-HPO ligands, zinc is much more well absorbed than the simple aqueous inorganic ion and its phytate complex.9

However, the exposure to high levels of zinc may cause acute zinc intoxication. Although this is a rare incident, the toxic effects of this metal ion due to long-term and excessive supplementation delays the uptake of copper, which is associated with several pathologies and neurodegenerative diseases.10 In fact, the ability of 3,4-HPO ligands to chelate bio-relevant metal ions such as Cu(ii), Zn(ii) and Fe(iii) is being investigated for potential use in Alzheimer's disease, due to their ability to disrupt amyloid-beta aggregates through the interaction with the metal ions in plaques.8,11 Furthermore, other pharmaceutical purposes were identified for 3,4-HPO ligands as appropriate chelators and carriers of the zinc metal ion. For example, some 3,4-HPO Zn(ii) complexes had an insulin-like action. In particular, the bis(1,2-dimethyl-3-hydroxy-4(1H)-pyridinonate)Zn(ii) complex significantly decreased the blood glucose levels in in vivo experiments.6 The same Zn(ii) complex has showed potential anti-inflammatory properties due to its ability to inhibit the neutrophil's oxidative burst. Hence, Zn(ii) complexes may also be valuable assets for the treatment of the oxidative damage in several disorders, having advantages over inorganic zinc in terms of bioavailability and pharmaceutical efficacy. Lastly, other zinc complexes (complexed with Hdmpp and other 3,4-HPO ligands) were also pointed out as potential inhibitors of the Zn(ii)-dependent matrix metalloproteinases, which are often related with cancer and inflammatory diseases.12

Zinc complexes may occur in different coordination numbers (most typically of four, five and six), which are characterized by fast ligand exchange.13,14 The crystallographic geometry of a Zn(ii) ion complexed with the Hdmpp ligand has been characterized.9 Within this complex, the zinc is five-coordinated with a distorted square-pyramidal geometry. However, distinct five-coordination geometries were also found for a few zinc complexes, as the Zn(ii) complex coordinated with one Hdmpp ligand into a mixed hydro-tris(3,5-phenylmethylpyrazolyl)borate ligand system, which presented a distorted trigonal bipyramidal geometry.12 This geometry is also prevalent in the catalytic sites of several metalloenzymes, such as the angiotensin converting enzyme,15 matrix metalloproteinases,12 and a modelled carbonic anhydrase.9 Furthermore, a few zinc complexes also showed six-coordination geometries, such as Zn(ii)-bis-maltolate9 and zinc complexed with 3-hydroxy-2-methyl-1-phenyl-4(1H)-pyridinone.8 The latter crystalized as a tetramer with four metals per eight ligands, and possessed two different zinc centers: (i) one that was coordinated to two ligands and one water molecule in a five-coordinated distorted square-pyramidal geometry; (ii) the other coordinated by six oxygen atoms from three ligands, adopting a distorted octahedral geometry.

To evaluate the eventual use of 3,4-HPO ligands for Zn(ii) removal and carriage, information about lipophilicity, their partition and translocation properties in water-membrane phases is extremely important.16 While a lipophilic chelator might decrease intracellular metal ion stores, as they penetrate cells more readily; the activity of hydrophilic chelators is more limited to extracellular metal ion pools and their renal excretion should be facilitated. Conversely, lipophilic chelators may also redistribute toxic metal ions to more vulnerable organs.17,18 Hence, lipophilicity is a crucial aspect to consider when developing chelating agents.

Several structures of Cu(ii) complexes in solution were previously characterized by electron paramagnetic resonance (EPR) spectroscopy, where the affinity for hydrophobic environments was also studied.7 However, considering that the Zn(ii) ion is “EPR-silent”, a computational approach was used to characterize the interactions of a set of 3,4-HPO Zn(ii) complexes (and respective neutral ligands of different lipophilicities) with hydrated bilayer systems, and their partition between the bilayer and water phases. Both conventional and enhanced sampling molecular dynamics (MD) simulations were employed to this regard. Although we have focused on Zn(ii) complexes, by also studying the lipophilicity of the chelating molecules, this study has a wider applicability, since these agents are also known to chelate other relevant metals, such as iron and copper.

Methods

Parameterization of Zn(ii) complexes

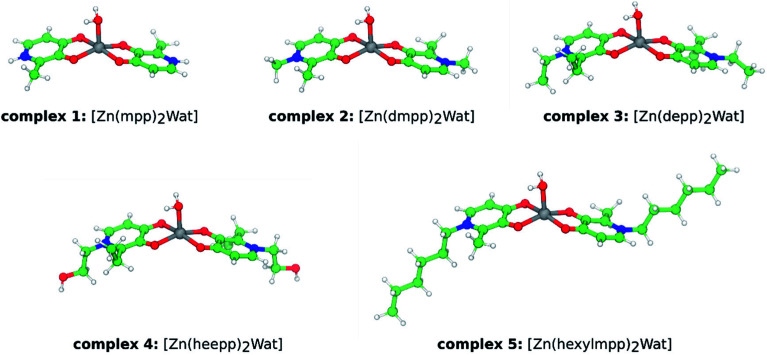
We have followed a bonded model approach for the parameterization of the zinc complexes detailed in Fig. 2.19 The methodology has been previously described in the literature in full detail.20 The parameterization for the metal coordination sphere of the Zn(ii) complexes shown in Fig. 2 was based on the available X-ray structure of complex 2, [Zn(dmpp)2Wat].9 The geometry was optimized with B3LYP/6-31G(d,p):SDD (mixed basis set with the effective core potential SDD on zinc and all electron orbitals on the other atoms); linear transit scans (at the same level of theory) for bonds and angles involving zinc were conducted for extracting the harmonic force constants. Dihedral parameters were zeroth, as customary in this bonded-model approach. The derived force constants were then applied to every complex detailed in this study. The equilibrium bond distances and angles were taken from the optimized values of each complex (these have not presented relevant deviations among the entire set of complexes). Non-bonded van der Waals parameters were extracted from the literature.21 For atomic point charge calculations, a RESP approach22 was used with the B3LYP/6-311++G(3df,3pd) level of theory in previously B3LYP/6-31G(d,p):SDD optimized structures. The two 3-hydroxy-4-pyridinone (3,4-HPO) ligands in each complex were considered charge and parameter equivalent (force constants and equilibrium bond distances were averaged). Additionally, 1–4 interactions involving the water ligand hydrogen atoms were excluded, to maintain the overall geometry of the complexes. Otherwise, the square based pyramidal geometry was compromised. The different protonated ligands of the Zn(ii) complexes (see Fig. 1) were parameterized with the GAFF23 using the ANTECHAMBER suite available in the Amber 12 software.24 Full details over the parameterization of the simulated molecules are enclosed in the ESI section (see ESI, Fig. ESI-1†). Quantum-mechanics calculations were performed with the Gaussian 09 software.25

Fig. 2. Ball-and-stick representation of the studied Zn(ii) complexes. The abbreviated complexes' name is also depicted.

Fig. 2

Open in a new tab

Membrane models and their stability

The membrane systems employed in this study were modelled with the SLipids FF.26,27 This FF has provided excellent results over geometry and energetics,28 comparing to other available FF options in the literature, such as CHARMM36,29,30 or GAFFlipids.31 Two membrane models were employed: (i) one comprising 32 DMPC phospholipids per layer (32 : 32 model); and (ii) a second model containing 150 DMPC lipids per layer (150 : 150 model). Hydration level was close to 50 water molecules per lipid (as typically employed in the literature). Additionally, NaCl (0.15 M) was added to the system. These two models were constructed with the CHARMM-GUI webserver.32 After generating the initial model structures, these were submitted to geometry optimization and 100 ns conventional molecular dynamics (cMD) in the conditions described subsequently. Their geometry and dynamic stability were assessed, considering available experimental data. Overall, the two models showed a close resemblance to experimental results (see ESI, Table ESI-1, Fig. ESI-2 and ESI-3†).33–39 The last structure from this stage and for both models, was employed in the subsequent analysis of the partition of the compounds in Fig. 2, or respective neutral ligands in Fig. 1.

Conventional molecular dynamics (cMD) simulations

As described previously, two membrane models were employed in this study. These were both used for cMD simulations of the complexes in Fig. 2. The complexes were inserted in the hydrated bilayer systems. For the 32 : 32 DMPC system, only one complex was modelled in the simulation box. It was placed in the water phase on top of one of the layers, and energy minimized and equilibrated for 20 ns (with position restraints). Subsequently, the restraints were removed, and each system was simulated for 140 ns (the [Zn(heepp)2Wat] complex was simulated an additional 40 ns, since no insertion was observed within 140 ns of simulation). A similar protocol was applied to the 150 : 150 system. However, instead of one, four complexes were inserted on top of each layer (a total of eight complexes). Each system was simulated for 140 ns as well. For the 32 : 32 and 150 : 150 systems, the complexes' average concentration in the simulation box was 9.98 ± 0.01 mM; and 16.13 ± 0.01 mM, respectively.

The employed protocol conditions were as following. All simulations were performed with the GROMACS software (version 5.1).40,41 The molecules' parameters (generated previously) were converted to gromacs topology files through the acpype.py script.42 The TIP3P water model was employed, as it is frequently employed with AMBER-generated parameters. Simulations were performed taking advantage of native GPU acceleration with the Verlet cut-off scheme. A non-bonded cut-off value of 1.2 nm was employed. The LINCS constraint algorithm was applied to all bonds,43 which allowed for an integration time step of 2 fs. Temperature was set to 310.15 K with the V-rescale thermostat,44 and a semi-isotropic pressure scaling to 1 atm was maintained with the Parrinello–Rahman barostat (mimicking physiological conditions).45,46 Periodic boundary conditions were considered. Long-range electrostatic interactions were treated by a Particle Mesh Ewald (PME) scheme.47 The results were analyzed with GROMACS tools, and simulations were animated and visually inspected with the VMD program (version 1.9).48

Potential-of-mean force (PMF) simulations

Molecules of interest were positioned on the water phase on top of one of the layers of the membrane of the previously equilibrated DMPC 32 : 32 system. The system was then minimized and equilibrated for an additional 20 ns with the molecule's atomic positions restrained. A constant-force pulling simulation along the normal of the bilayer was performed, for a maximum of 10 ns and with force constants ranging from 35 to 90 kJ mol−1 nm−1. When the center of mass (COM) distance along the bilayer's normal between the solutes and the bilayer was −0.2 nm – this corresponded to a position immediately below the bilayer's COM (at 0.0 nm), each compound was restrained with an umbrella potential and equilibrated for an additional 15 ns. The compounds were then pulled in the reversed direction (of the previous pull) towards the water slab, in similar conditions as previously discussed. Pulling from the middle of the bilayer to the water phase has been described in the literature as a faster converging protocol than the opposite situation.49,50 This second pull-simulation was used to extract conformations spaced by 0.1 nm, considering the COM distance between the solutes and the bilayer, thus describing our reaction coordinate for the umbrella sampling (US) simulations. A total of 35 US windows were simulated, comprising the COM distance of [−0.2; 3.2] nm, going from the bilayer (COM distance of ca. [−0.2; 2.5] nm) to the water phase (COM distances larger than 2.5 nm, approximately). For each US window simulation, an equilibration of 15 ns was performed in the NPT ensemble, prior to production simulations of 50 ns per window. An umbrella force constant of 1250 kJ mol−1 nm−2 was applied. A cylinder reference geometry was employed with a 1.5 nm radius. The analysis of the PMFs was conducted with the WHAM tool51 in GROMACS 5.1 software over the last 35 ns of the production simulations. Bootstrapping analysis (200 bootstraps) was also performed to assess for the error of the PMF.

Results and discussion

The results and discussion section were divided into two parts. The first part discusses the partition coefficients of each uncomplexed neutral ligand (see Fig. 1) between the water and the bilayer phases (Kmem). We also evaluated the influence of zinc complexation on the partition coefficients considering one of the ligands, 1,2-dimethyl-3-hydroxy-4-pyridinone (Hdmpp), by evaluating the partition of the corresponding Zn(ii) complex (complex 2, see Fig. 2). To our knowledge, this was one of the first studies that has produced PMFs for the translocation of transition-metal complexes. The partition coefficients were calculated from the PMFs generated with US simulations, as the molecules permeated the bilayer. In the second part, we address the results considering the cMD simulations of each Zn(ii) complex in two simulation settings: (i) starting with only one complex in the water phase (in a 32 : 32 hydrated bilayer system); and (ii) starting with eight complexes in the water phase (in a 150 : 150 hydrated bilayer system). We wanted to evaluate if all complexes penetrated the bilayer phase (and how deep was their insertion into the bilayer), and the impact of an increased concentration of the complexes in the water phase.

Potential-of-mean force (PMF) results

With the PMFs we can calculate partition coefficients and to know the affinity of the compounds for each region of the system (along the reaction coordinate), as they permeate the bilayer. The binding free energy can be obtained from the PMF, using the following expression: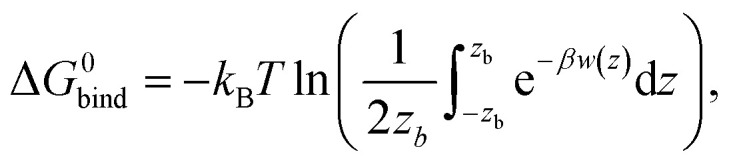graphic file with name c8ra03602k-t1.jpgwhere zb is the distance when w(z) = 0, β = 1/kBT and kB is the Boltzmann constant and T the absolute temperature. The partition coefficient of the solute, between the membrane and aqueous phases, can then be derived according to 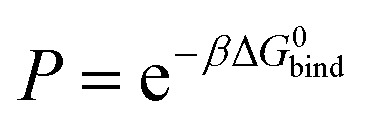Inline graphic.52

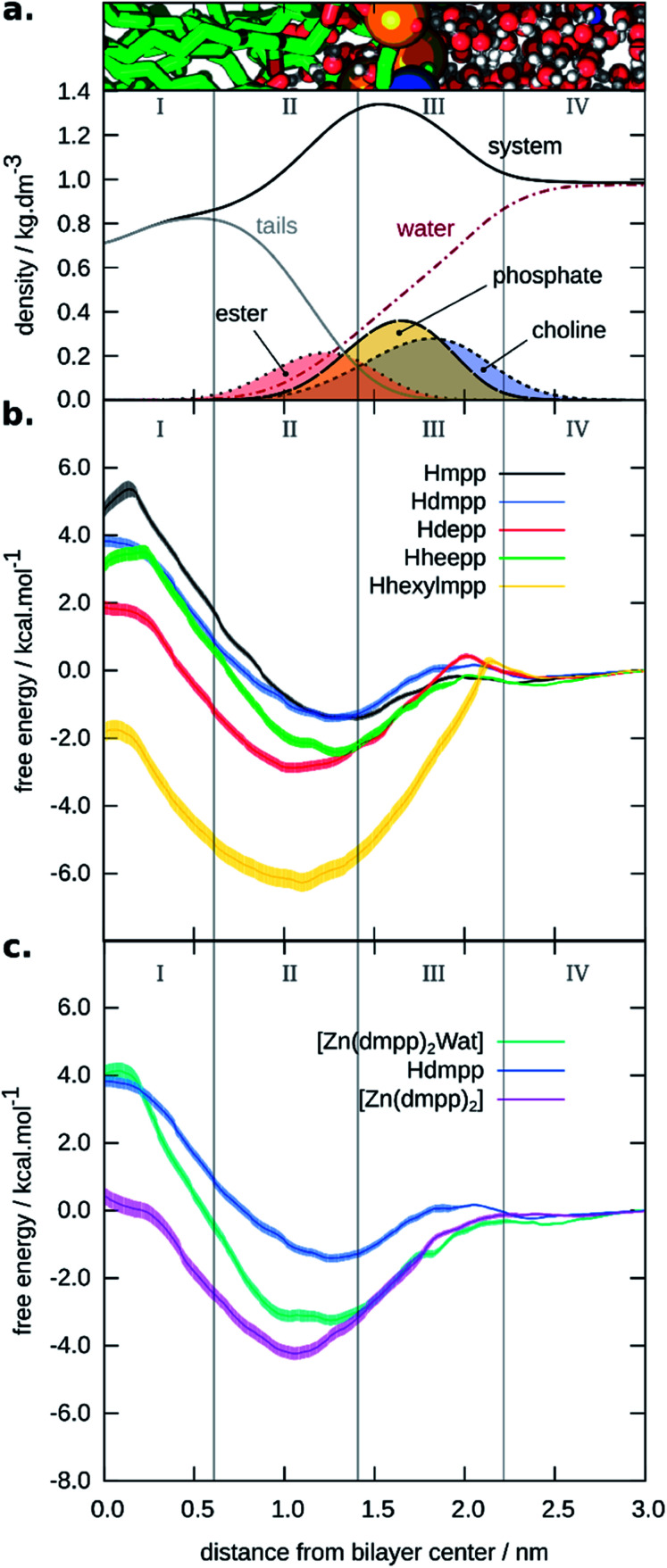
In addition, by comparing minimum and maximum free energies values, one can qualitatively predict which compound should permeate the membrane faster. In Fig. 3, we display the PMF for the five neutral ligands shown in Fig. 1 (see Fig. 3b). We also depict the four membrane regions (see Fig. 3a), as described in similar works.53 These were defined taking into account specific densities of the hydrated bilayer system: region I, containing only hydrophobic lipid tails; region II, containing both hydrophobic tails up to the intersection of the choline and lipid tails groups' region; region III, where the systems' density has its peak up to half the density of the choline group; and region IV, comprised mainly of bulk water and the beginning of the polar head-group region of the lipid bilayer.

Fig. 3. Graphical representation of the generated PMFs. (a). Four-region model defined by the densities of the system's hydrophilic and hydrophobic components. On the top, we show an illustration of the bilayers' considered distance. (b). PMFs for the neutral ligands; and (c). PMF of the tetra-coordinated and penta-coordinated Zn(ii) complex 2, with the PMF of Hdmpp shown for comparison.

Fig. 3

Open in a new tab

From the PMFs we observed that Hhexylmpp presented the highest affinity for the membrane phase. Next, came Hdepp and Hheepp with the former showing the highest affinity among the two. Lastly, the compounds showing the lowest affinity for the bilayer were Hmpp and Hdmpp. The region in which they preferentially were located – corresponding to the minimum of the PMF, was region II or the interface between regions II and III (in the case of the Hmpp ligand). Region II is the most heterogeneous region containing both hydrophobic and hydrophilic (both lipid and some water molecules) components.

Overall, the partition followed the hydrophobicity of the compounds, in which the neutral ligands with the most hydrophobic substituents, Hhexylmpp and Hdepp, showed the highest partition to the membrane. With one hexyl group substituent in the 3,4-HPO ring, Hhexylmpp showed a partition at least two orders of magnitude higher, in terms of Kmem, relatively to the other neutral ligands.

To evaluate the differences between ligands and respective Zn(ii) complexes, we have also assessed the partition considering one test case – complex 2: [Zn(dmpp)2Wat]. The results shown in Fig. 3 (see Fig. 3c) support that the Zn(ii) complex had a higher affinity to the bilayer than the respective neutral ligand (in this case Hdmpp). However, the barrier to cross was higher when a water molecule was also coordinated to zinc(ii), making a penta-coordinated complex. In this case, the results could be hampered by the bonded model approach used here. We cannot exclude the loss of the axial water ligand as these complexes translocate the bilayer. If this happens, we would expect a smaller barrier for crossing for the tetra-coordinated zinc complex. Also, as six-coordinated Zn(ii) complexes (two axial water ligands) have also been described for pyranone derivatives,9 we cannot exclude possible changes of the coordination of these complexes in more hydrophilic environments.

We have not accessed to what extent is the chelation influenced by the media, and this is scarcely discussed in the literature (the discussion always prevails in terms of pH speciation). We would expect that these Zn(ii) complexes could be influenced by the surrounding media, as proposed by others.8 In that sense, we have performed a PMF estimate for the tetra-coordinated Zn(ii) complex 2, in order to study its partition within the bilayer. The PMFs in Fig. 3 (see Fig. 3c) comparing both tetrahedral and distorted square-based pyramidal Zn(ii) complex 2, showed that the tetra-coordinated complex presented a higher affinity to the membrane phase, particularly considering regions I and II. This was in accordance to our initial supposition.

By calculating the radial distribution function (RDF) and following the number of water molecules surrounding the zinc(ii) ion along the umbrella sampling reaction coordinate (the bilayer's normal), we saw a distinct profile when comparing [Zn(dmpp)2Wat] and [Zn(dmpp)2] (see ESI, Fig. ESI-4†). On the one hand, we saw that [Zn(dmpp)2Wat] was able to extract more water molecules as it permeated the bilayer, which can justify its lower affinity to regions I and II of the hydrated bilayer system. On the other hand, for the umbrella sampling simulation of [Zn(dmpp)2], fewer water molecules were found in region II, and almost no water molecule was found in region I (considering a 0.36 nm range distance to the zinc atom).

Membrane binding free energies and log Kmem values are also shown in Table 1. We saw that the ligand with the highest partition constant and affinity to the bilayer was Hhexylmpp. In addition, it was also apparent the highest log Kmem of complex 2, relative to the isolated neutral ligand that constitutes the complex, Hdmpp. The lipophilicity of the complexes is always increased since more than one ligand are usually present. For Zn, two ligands are present, and the external solvation sphere bears two ligands. The effect is even more noted for Fe complexes since the stoichiometry is normally of 1 : 3. The partition of the tetra-coordinated Zn(ii) complex, [Zn(dmpp)2], was also higher than the respective distorted square-pyramidal complex, [Zn(dmpp)2Wat].

Free energy binding values (ΔGbind), membrane partition coefficients (log Kmem), and permeability estimates (PΔG) obtained from the PMFs of the presented moleculesa.

Molecule ΔGbind/kcal mol−1 log Kmem Permeability predictor, PΔG
Hmpp −0.53 ± 0.07 0.38 ± 0.05 0.091 ± 0.0034
Hdmpp −0.48 ± 0.10 0.34 ± 0.07 0.12 ± 0.0046
Hdepp −1.83 ± 0.14 1.29 ± 0.10 0.13 ± 0.0066
Hheepp −1.31 ± 0.13 0.92 ± 0.09 0.10 ± 0.0044
Hhexylmpp −5.17 ± 0.28 3.64 ± 0.20 0.094 ± 0.0043
[Zn(dmpp)2Wat] −2.21 ± 0.16 1.55 ± 0.11 0.084 ± 0.0034
[Zn(dmpp)2] −3.02 ± 0.19 2.13 ± 0.14 0.13 ± 0.0090
Open in a new tab
a

The errors were derived from the bootstrapping analysis of the PMFs. More details can be found in the ESI.54

Orsi M. and Essex J. W.55 have proposed a qualitative assessment of the permeability of compounds. They defined the propensity of a compound to cross the membrane using a “permeability predictor”, PΔG, defined through the following expression: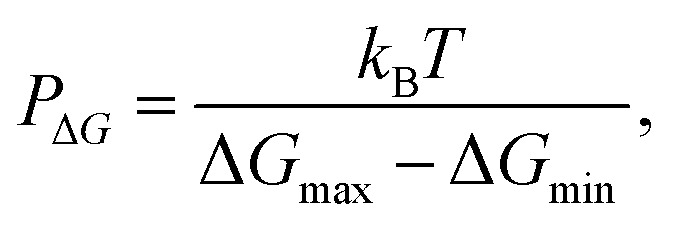graphic file with name c8ra03602k-t3.jpgwhere ΔGmax and ΔGmin are maximum and minimum values of the permeant's PMF, and kBT the standard free energy factor given by the product of the Boltzmann constant, kB, with the temperature, T. The results indicated that permeability is higher for the neutral ligands Hdmpp and Hdepp, and for the tetra-coordinated Zn(ii) complex, [Zn(dmpp)2]. We also saw that the permeability was substantially reduced for the penta-coordinated Zn(ii) complex, [Zn(dmpp)2Wat]. Obviously, these determinations of permeability are highly qualitative, and improved estimates including the determination of diffusivities would be necessary to provide more quantitative results. However, methods for doing so are still prone to pronounced discrepancies with experimental reference data, as these require long equilibration times and extended analysis.56,57

Regarding the fast ligand exchange and flexible coordination number observed for some zinc complexes, it is probable that the [Zn(dmpp)2Wat] complex may lose its axial water when entering the membrane. There is also experimental evidence of de-metallation of zinc–salophen complexes through interactions with phosphate groups of large unilamellar vesicles of POPC.58 In addition, the Zn(ii) stability constants for the 3,4-HPO ligands are much lower (105 times) than those of Cu(ii),7 which may be related to an easier change in the zinc complex coordination number.

Zn(ii) complexes' distribution and self-aggregation in hydrated bilayer systems

Five Zn(ii) complexes were chosen to study their interaction with lipid phases, here modelled as bilayers composed of DMPC phospholipids. These five Zn(ii) complexes, coordinated to different 3,4-HPO ligands, were specifically chosen due to their proved success as metal chelators for iron and copper metal ions.7 In addition, their distinct lipophilicities will allow to rationalize which are the most suitable complexes for transporting zinc across biological membranes. In the present study, we have used the crystallographic geometry of a Zn(ii) ion complexed with the dmpp 3,4-HPO ligand, as a starting structure.9 Within this complex, the zinc is penta-coordinated with a distorted square-pyramidal geometry (see Fig. 2). The metal ion coordinates both dmpp ligands (with the hydroxy and ketonic oxygen atoms in a trans-chelating orientation) and one axial water molecule. Although six more water molecules are present in the crystal, these do not interact directly with the zinc ion.

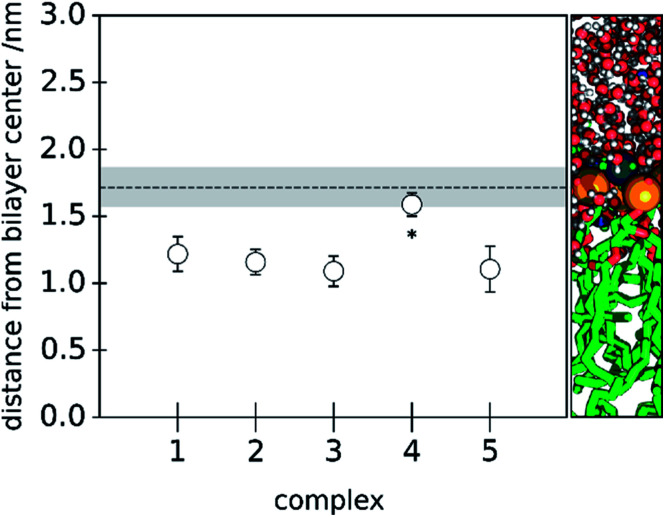
Initially, each complex was simulated in a hydrated 32 : 32 lipid bilayer system. In Fig. 4, we show the center-of-mass position of each complex relative to the bilayers' normal. As a reference, we also show the average center-of-mass position of all phosphorus atoms present in the corresponding layer.

Fig. 4. Average distance (with standard deviation) of the five Zn(ii) complexes to the bilayers' center, considering the bilayers' normal. The relative COM position considering all the phosphorus atoms in one of the layers and the bilayers' COM is depicted as a dashed line (with the phosphorus atoms COM's standard deviation in grey). On the right, we show an illustration of the bilayers' considered distance. The results express an analysis performed over the last 20 ns of the cMD simulation of the 32 : 32 system for each of the studied complexes. For the complex marked with an asterisk, the cMD simulations were prolonged.

Fig. 4

Open in a new tab

The different Zn(ii) complexes were purposely placed distant to the bilayer to evaluate their affinity for the lipid phase. We observed a deep bilayer insertion of the complexes 1, 2, 3 and 5 within the 32 : 32 membrane model, whilst complex 4 ([Zn(heepp)2Wat]) showed a smaller insertion in the studied time window. An increased polarity of the substituents of the pyridinone ring could justify the higher affinity for the water phase, or to the more polar region of the bilayer. These results seem also consistent with one EPR study on 3,4-HPO copper(ii) complexes,7 evaluating the solvent interactions of [Cu(ii)(depp)2], [Cu(ii)(heepp)2] and [Cu(ii)(hexylmpp)2] complexes with liposome suspensions, where [Cu(ii)(heepp)2] interacted preferentially with the water phase; [Cu(ii)(hexylmpp)2] was clearly inserted in the lipid phase; and [Cu(ii)(depp)2] seemed to coexist in both phases. However, we believe that with extended time scales, [Zn(ii)(heepp)2Wat] could penetrate deeper in the bilayer, as suggested in the analysis of the PMF of the neutral Hheepp ligand.

We have also analyzed the deuterium order parameters of the acyl chains and the area per lipid in the last 20 ns of the cMD simulations. In this last portion of the simulations all the complexes were interacting with the lipid phase (even though at different depths). The results are shown in the ESI (see ESI, Fig. ESI-5 and Table ESI-2†). Relatively to the deuterium order parameters, a slight decrease was observed for [Zn(hexylmpp)2Wat]. This is indicative of a higher disorder of the acyl chains. The increase in the area per lipid was also more substantial for this complex. More drastic effects should be expected in the presence of a higher number of metal complexes.

To better understand the partition of the Zn(ii) complexes to membrane phases, we have decided to increase the concentration of the complexes in water. Doing so, we were closer to experimental conditions, and so to the crowded-environments that could play a role in the dynamics of these compounds. For this situation, eight complexes were studied in each simulation setting. It is interesting to observe the self-aggregation between molecules of Zn(ii) complexes as shown by the panels in Fig. 5, representing the last structure of the cMD simulation of the 150 : 150 system for each studied complex. We saw that complexes 2 to 5 are prone for self-assembly, especially complex 5, in which seven of the eight complexes in solution were aggregated. The more hydrophobic character of their substituents (relative to the other complexes) is probably inducing this behavior.

Fig. 5. Representation of the last structure of the cMD simulation of each Zn(ii) complex, considering the 150 : 150 bilayer system. Membrane is depicted in black and white in sticks and phosphorous atoms in spheres. Zn(ii) complexes are represented in atom type-colored spheres: C – green; O – red; N – blue; and H – white. Water molecules are not displayed for simplicity.

Fig. 5

Open in a new tab

Similar self-assembled behaviors were observed for other Zn(ii) complexes by experimental techniques, such as X-ray data, NMR, UV/vis and circular dichroism (CD) spectroscopic data. As already mentioned, the Zn(ii) complex with the 3-hydroxy-2-methyl-1-phenyl-4(1H)-pyridinone ligand crystalizes as a tetramer with four metals per eight ligands,8 while the bis(salicylaldiminato) Zn(ii) and trans-1,2-diaminocyclohexane Zn(ii) Schiff-base complexes aggregate either in solution or in solid state, creating supramolecular structures.59 Transmission electron microscopy (TEM) and scanning electron microscopy (SEM) also revealed the formation of self-interacting structures of Zn(ii) salphen complexes, in which the zinc center of one salphen unit interacts with the phenolic oxygen of another one, forming dimeric assemblies.60

The membrane deuterium order parameters were also analyzed for the cMD simulation with eight [Zn(mpp)2Wat] complexes, because this was the only case where all complexes were interacting with the membrane in the last stages of the simulation. We did not observe significant changes in the order parameters of the acyl chains (see ESI, Fig. ESI-5†). This could be related to the more hydrophilic character displayed by the Hmpp ligand, which could limit the penetration of the complex into the membrane.

Conclusion

The results of this multi-approach computational study have helped us to infer about the partition of 3,4-HPO ligands and of the respective Zn(ii) complexes to lipid phases. By developing the simulations in a bilayer system, rather than using octanol/water systems, we can better correlate with biological membranes.

Of the studied ligands, the ligand with the highest partition to the bilayer was Hhexylmpp, with at least two orders of magnitude higher Kmem when compared to the other ligands. Its zinc complex, [Zn(hexylmpp)2Wat] was also prone to self-aggregation, when a higher number of complexes were simulated. Since we have studied the partition of the isolated chelating molecules, and these are known to chelate other metals than solely Zn(ii) ions, this study has a broad appeal.

Furthermore, we saw that the partition of the corresponding zinc complex (considering one of the studied ligands, Hdmpp) had a higher partition than the isolated ligand. We have also discussed possible mechanisms for the permeation of Zn(ii) complexes. Namely, we discussed the possibility of axial ligand (water molecule) loss that could increase the permeability of the complex. To our knowledge, this was one of the first studies that has produced PMFs for the permeation of transition-metal complexes. Conversely, although this approach helped us to study the partition and qualitatively assess the permeability of the zinc complex with Hdmpp, we could not describe possible ligand-exchange phenomena upon membrane permeation, because we used a bonded model approach. Other approaches, such as non-bonded force field models, or multi-resolution quantum mechanics/molecular mechanics (QM/MM) methods could provide the necessary details on this aspect. Indeed, some authors have described the dynamics of zinc(ii) complexes in solution using ab initio MD.14 Future efforts on this aspect could be quite interesting to explore.

We also evaluated the self-aggregation of Zn(ii) complexes in hydrated bilayer systems, as we increased the concentration of the complexes in the media. We observed that more hydrophobic Zn(ii) complexes were prone for self-aggregation. This might influence the partition and permeation of the complexes. Although some computational studies have explored the solubility of solutes in membrane models, few have explored the effects of self-aggregation to membrane partition.61,62 The stacking of fluoroquinolones, for instance, has been speculated to influence the partition to the membrane, since the electrostatic potential of the stacked fluoroquinolones would be reduced.62 Drug aggregates were also described to delay membrane penetration.63 Hence, future studies addressing the impact of self-aggregation to the partition and permeation of these chelating agents should be an important venue of research.

The impact of 3,4-HPO ligands to biomedical applications has already been extensively described in the literature. We provided yet another level of information that can have a direct impact in the research comprising these molecules, and considering a set of Zn(ii) complexes that are often “silent” in experimental throughputs. These results can help to a more directed experimental approach focused on this class of compounds.

Conflicts of interest

There are no conflicts to declare.

Supplementary Material

RA-008-C8RA03602K-s001

Acknowledgments

This work received financial support from the following institutions: European Union (FEDER funds POCI/01/0145/FEDER/007728) and National Funds (FCT/MEC, Fundação para a Ciência e Tecnologia (FCT) and Ministério da Educação e Ciência) under the Partnership Agreement PT2020 UID/MULTI/04378/2013, SFRH/BD/87434/2012, IF/01355/2014 and UID/QUI/50006/2013-POCI/01/0145/FEDER/007265 (LAQV/REQUIMTE); NORTE-01-0145-FEDER-000024, supported by Norte Portugal Regional Operational Programme (NORTE 2020), under the PORTUGAL 2020 Partnership Agreement, through the European Regional Development Fund (ERDF). J. T. S. C. and N. F. B. thank FCT for their PhD (SFRH/BD/87434/2012) and IF (IF/01355/2014) starting grants, respectively.

†

Electronic supplementary information (ESI) available: Further details on the Zn(ii) complexes' parameterization and on the estimation of the membrane partition errors. Membrane validation results. Results for the radial distribution function (RDF) of water as a function of the distance to zinc. Supplementary results for the effects of the zinc complexes' insertion into the membrane structure. See DOI: 10.1039/c8ra03602k

‡

Author Contributions: The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.

References

  1. Moniz T. Leite A. Silva T. Gameiro P. Gomes M. S. de Castro B. Rangel M. The influence of functional groups on the permeation and distribution of antimycobacterial rhodamine chelators. J. Inorg. Biochem. 2017;175:138–147. doi: 10.1016/j.jinorgbio.2017.07.017. [DOI] [PubMed] [Google Scholar]
  2. González A. Mesquita R. B. R. Avivar J. Moniz T. Rangel M. Cerdà V. Rangel A. O. S. S. Microsequential injection lab-on-valve system for the spectrophotometric bi-parametric determination of iron and copper in natural waters. Talanta. 2017;167:703–708. doi: 10.1016/j.talanta.2017.02.055. [DOI] [PubMed] [Google Scholar]
  3. Santos C. S. Carvalho S. M. P. Leite A. Moniz T. Roriz M. Rangel A. O. S. S. Rangel M. Vasconcelos M. W. Effect of tris(3-hydroxy-4-pyridinonate) iron(iii) complexes on iron uptake and storage in soybean (Glycine max L.) Plant Physiol. Biochem. 2016;106:91–100. doi: 10.1016/j.plaphy.2016.04.050. [DOI] [PubMed] [Google Scholar]
  4. Burgess J. Rangel M. Adv. Inorg. Chem. 2008;60:167–243. doi: 10.1016/S0898-8838(08)00005-6. [DOI] [Google Scholar]
  5. Queiros C. Amorim M. J. Leite A. Ferreira M. Gameiro P. de Castro B. Biernacki K. Magalhães A. Burgess J. Rangel M. Nickel(ii) and Cobalt(ii) 3-Hydroxy-4-pyridinone Complexes: Synthesis, Characterization and Speciation Studies in Aqueous Solution. Eur. J. Inorg. Chem. 2011;2011:131–140. doi: 10.1002/ejic.201000849. [DOI] [Google Scholar]
  6. Moniz T. Amorim M. J. Ferreira R. Nunes A. Silva A. Queirós C. Leite A. Gameiro P. Sarmento B. Remião F. Yoshikawa Y. Sakurai H. Rangel M. Investigation of the insulin-like properties of zinc(ii) complexes of 3-hydroxy-4-pyridinones: Identification of a compound with glucose lowering effect in STZ-induced type I diabetic animals. J. Inorg. Biochem. 2011;105:1675–1682. doi: 10.1016/j.jinorgbio.2011.09.005. [DOI] [PubMed] [Google Scholar]
  7. Rangel M. Leite A. Silva A. M. N. Moniz T. Nunes A. Amorim M. J. Queiros C. Cunha-Silva L. Gameiro P. Burgess J. Distinctive EPR signals provide an understanding of the affinity of bis-(3-hydroxy-4-pyridinonato) copper(ii) complexes for hydrophobic environments. Dalton Trans. 2014;43:9722–9731. doi: 10.1039/C4DT00642A. [DOI] [PubMed] [Google Scholar]
  8. Telpoukhovskaia M. A. Rodríguez-Rodríguez C. Scott L. E. Page B. D. G. Patrick B. O. Orvig C. Synthesis, characterization, and cytotoxicity studies of Cu(ii), Zn(ii), and Fe(iii) complexes of N-derivatized 3-hydroxy-4-pyridiones. J. Inorg. Biochem. 2014;132:59–66. doi: 10.1016/j.jinorgbio.2013.12.003. [DOI] [PubMed] [Google Scholar]
  9. Ahmed S. I. Burgess J. Fawcett J. Parsons S. A. Russell D. R. Laurie S. H. The structures of bis-maltolato-zinc(ii) and of bis-3-hydroxy-1,2-dimethyl-4-pyridinonato–zinc(ii) and –lead(ii) Polyhedron. 2000;19:129–135. doi: 10.1016/S0277-5387(99)00330-7. [DOI] [Google Scholar]
  10. Plum L. M. Rink L. Haase H. The Essential Toxin: Impact of Zinc on Human Health. Int. J. Environ. Res. Public Health. 2010;7:1342–1365. doi: 10.3390/ijerph7041342. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Telpoukhovskaia M. A. Rodriguez-Rodriguez C. Cawthray J. F. Scott L. E. Page B. D. G. Ali-Torres J. Sodupe M. Bailey G. A. Patrick B. O. Orvig C. 3-Hydroxy-4-pyridinone derivatives as metal ion and amyloid binding agents. Metallomics. 2014;6:249–262. doi: 10.1039/C3MT00135K. [DOI] [PubMed] [Google Scholar]
  12. Puerta D. T. Cohen S. M. Examination of Novel Zinc-Binding Groups for Use in Matrix Metalloproteinase Inhibitors. Inorg. Chem. 2003;42:3423–3430. doi: 10.1021/ic026029g. [DOI] [PubMed] [Google Scholar]
  13. Tamames B. Sousa S. F. Tamames J. Fernandes P. A. Ramos M. J. Analysis of zinc-ligand bond lengths in metalloproteins: Trends and patterns. Proteins: Struct., Funct., Bioinf. 2007;69:466–475. doi: 10.1002/prot.21536. [DOI] [PubMed] [Google Scholar]
  14. Rodriguez-Santiago L. Ali-Torres J. Vidossich P. Sodupe M. Coordination properties of a metal chelator clioquinol to Zn2+ studied by static DFT and ab initio molecular dynamics. Phys. Chem. Chem. Phys. 2015;17:13582–13589. doi: 10.1039/C5CP01615K. [DOI] [PubMed] [Google Scholar]
  15. Brás N. F. Fernandes P. A. Ramos M. J. QM/MM Study and MD Simulations on the Hypertension Regulator Angiotensin-Converting Enzyme. ACS Catal. 2014;4:2587–2597. doi: 10.1021/cs500093h. [DOI] [Google Scholar]
  16. Lachowicz J. I. Nurchi V. M. Crisponi G. Jaraquemada-Pelaez M. G. Arca M. Pintus A. Santos M. A. Quintanova C. Gano L. Szewczuk Z. Zoroddu M. A. Peana M. Domínguez-Martín A. Choquesillo-Lazarte D. Hydroxypyridinones with enhanced iron chelating properties. Synthesis, characterization and in vivo tests of 5-hydroxy-2-(hydroxymethyl)pyridine-4(1H)-one. Dalton Trans. 2016;45:6517–6528. doi: 10.1039/C6DT00129G. [DOI] [PubMed] [Google Scholar]
  17. Sears M. E. Sci. World J. 2013:2013. [Google Scholar]
  18. Hegde M. L. Bharathi P. Suram A. Venugopal C. Jagannathan R. Poddar P. Srinivas P. Sambamurti K. Rao K. J. Scancar J. Messori L. Zecca L. Zatta P. Challenges Associated with Metal Chelation Therapy in Alzheimer's Disease. J. Alzheimer's Dis. 2009;17:457–467. doi: 10.3233/JAD-2009-1068. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Li P. Merz K. M. Metal Ion Modeling Using Classical Mechanics. Chem. Rev. 2017;117:1564–1686. doi: 10.1021/acs.chemrev.6b00440. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Neves R. P. P. Sousa S. F. Fernandes P. A. Ramos M. J. Parameters for Molecular Dynamics Simulations of Manganese-Containing Metalloproteins. J. Chem. Theory Comput. 2013;9:2718–2732. doi: 10.1021/ct400055v. [DOI] [PubMed] [Google Scholar]
  21. Babu C. S. Lim C. Empirical Force Fields for Biologically Active Divalent Metal Cations in Water. J. Phys. Chem. A. 2006;110:691–699. doi: 10.1021/jp054177x. [DOI] [PubMed] [Google Scholar]
  22. Bayly C. I. Cieplak P. Cornell W. Kollman P. A. A well-behaved electrostatic potential based method using charge restraints for deriving atomic charges: the RESP model. J. Phys. Chem. 1993;97:10269–10280. doi: 10.1021/j100142a004. [DOI] [Google Scholar]
  23. Wang J. Wolf R. M. Caldwell J. W. Kollman P. A. Case D. A. Development and testing of a general amber force field. J. Comput. Chem. 2004;25:1157–1174. doi: 10.1002/jcc.20035. [DOI] [PubMed] [Google Scholar]
  24. Wang J. Wang W. Kollman P. A. Case D. A. Automatic atom type and bond type perception in molecular mechanical calculations. J. Mol. Graph. Model. 2006;25:247–260. doi: 10.1016/j.jmgm.2005.12.005. [DOI] [PubMed] [Google Scholar]
  25. Frisch M. J., et al., Gaussian 09, Revis. D.01, 2009
  26. Jämbeck J. P. M. Lyubartsev A. P. An Extension and Further Validation of an All-Atomistic Force Field for Biological Membranes. J. Chem. Theory Comput. 2012;8:2938–2948. doi: 10.1021/ct300342n. [DOI] [PubMed] [Google Scholar]
  27. Jämbeck J. P. M. Lyubartsev A. P. Derivation and Systematic Validation of a Refined All-Atom Force Field for Phosphatidylcholine Lipids. J. Phys. Chem. B. 2012;116:3164–3179. doi: 10.1021/jp212503e. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Paloncýová M. Fabre G. DeVane R. H. Trouillas P. Berka K. Otyepka M. Benchmarking of Force Fields for Molecule–Membrane Interactions. J. Chem. Theory Comput. 2014;10:4143–4151. doi: 10.1021/ct500419b. [DOI] [PubMed] [Google Scholar]
  29. Klauda J. B. Venable R. M. Freites J. A. O'Connor J. W. Tobias D. J. Mondragon-Ramirez C. Vorobyov I. MacKerell A. D. Pastor R. W. Update of the CHARMM All-Atom Additive Force Field for Lipids: Validation on Six Lipid Types. J. Phys. Chem. B. 2010;114:7830–7843. doi: 10.1021/jp101759q. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Pastor R. W. MacKerell A. D. Development of the CHARMM Force Field for Lipids. J. Phys. Chem. Lett. 2011;2:1526–1532. doi: 10.1021/jz200167q. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Dickson C. J. Rosso L. Betz R. M. Walker R. C. Gould I. R. GAFFlipid: a General Amber Force Field for the accurate molecular dynamics simulation of phospholipid. Soft Matter. 2012;8:9617–9627. doi: 10.1039/C2SM26007G. [DOI] [Google Scholar]
  32. Jo S. Kim T. Iyer V. G. Im W. CHARMM-GUI: A web-based graphical user interface for CHARMM. J. Comput. Chem. 2008;29:1859–1865. doi: 10.1002/jcc.20945. [DOI] [PubMed] [Google Scholar]
  33. Kučerka N. Nieh M.-P. Katsaras J. Fluid phase lipid areas and bilayer thicknesses of commonly used phosphatidylcholines as a function of temperature. Biochim. Biophys. Acta. 2011;1808:2761–2771. doi: 10.1016/j.bbamem.2011.07.022. [DOI] [PubMed] [Google Scholar]
  34. Kučerka N. Liu Y. Chu N. Petrache H. I. Tristram-Nagle S. Nagle J. F. Structure of Fully Hydrated Fluid Phase DMPC and DLPC Lipid Bilayers Using X-Ray Scattering from Oriented Multilamellar Arrays and from Unilamellar Vesicles. Biophys. J. 2018;88:2626–2637. doi: 10.1529/biophysj.104.056606. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Petrache H. I. Tristram-Nagle S. Nagle J. F. Fluid phase structure of EPC and DMPC bilayers. Chem. Phys. Lipids. 1998;95:83–94. doi: 10.1016/S0009-3084(98)00068-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Almeida P. F. F. Vaz W. L. C. Thompson T. E. Lateral diffusion in the liquid phases of dimyristoylphosphatidylcholine/cholesterol lipid bilayers: a free volume analysis. Biochemistry. 1992;31:6739–6747. doi: 10.1021/bi00144a013. [DOI] [PubMed] [Google Scholar]
  37. Orädd G. Lindblom G. Westerman P. W. Lateral Diffusion of Cholesterol and Dimyristoylphosphatidylcholine in a Lipid Bilayer Measured by Pulsed Field Gradient NMR Spectroscopy. Biophys. J. 2002;83:2702–2704. doi: 10.1016/S0006-3495(02)75279-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Douliez J. P. Léonard A. Dufourc E. J. Restatement of order parameters in biomembranes: calculation of C-C bond order parameters from C-D quadrupolar splittings. Biophys. J. 1995;68:1727–1739. doi: 10.1016/S0006-3495(95)80350-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Filippov A. Orädd G. Lindblom G. Influence of Cholesterol and Water Content on Phospholipid Lateral Diffusion in Bilayers. Langmuir. 2003;19:6397–6400. doi: 10.1021/la034222x. [DOI] [Google Scholar]
  40. Van Der Spoel D. Lindahl E. Hess B. Groenhof G. Mark A. E. Berendsen H. J. C. GROMACS: Fast, flexible, and free. J. Comput. Chem. 2005;26:1701–1718. doi: 10.1002/jcc.20291. [DOI] [PubMed] [Google Scholar]
  41. Pronk S. Páll S. Schulz R. Larsson P. Bjelkmar P. Apostolov R. Shirts M. R. Smith J. C. Kasson P. M. van der Spoel D. Hess B. Lindahl E. GROMACS 4.5: a high-throughput and highly parallel open source molecular simulation toolkit. Bioinformatics. 2013;29:845–854. doi: 10.1093/bioinformatics/btt055. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. da Silva A. W. Vranken W. F. ACPYPE - AnteChamber PYthon Parser interfacE. BMC Res. Notes. 2012;5:367. doi: 10.1186/1756-0500-5-367. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Hess B. Bekker H. Berendsen H. J. C. Fraaije J. G. E. M. LINCS: A Linear Constraint Solver for molecular simulations. J. Comput. Chem. 1997;18:1463–1472. doi: 10.1002/(SICI)1096-987X(199709)18:12<1463::AID-JCC4>3.0.CO;2-H. [DOI] [Google Scholar]
  44. Bussi G. Donadio D. Parrinello M. Canonical sampling through velocity rescaling. J. Chem. Phys. 2007;126:14101. doi: 10.1063/1.2408420. [DOI] [PubMed] [Google Scholar]
  45. Nosé S. Klein M. L. Constant pressure molecular dynamics for molecular systems. Mol. Phys. 1983;50:1055–1076. doi: 10.1080/00268978300102851. [DOI] [Google Scholar]
  46. Parrinello M. Rahman A. Polymorphic transitions in single crystals: A new molecular dynamics method. J. Appl. Phys. 1981;52:7182–7190. doi: 10.1063/1.328693. [DOI] [Google Scholar]
  47. Essmann U. Perera L. Berkowitz M. L. Darden T. Lee H. Pedersen L. G. A smooth particle mesh Ewald method. J. Chem. Phys. 1995;103:8577–8593. doi: 10.1063/1.470117. [DOI] [Google Scholar]
  48. Humphrey W. Dalke A. Schulten K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996;14:33–38. doi: 10.1016/0263-7855(96)00018-5. [DOI] [PubMed] [Google Scholar]
  49. Filipe H. A. L. Moreno M. J. Róg T. Vattulainen I. Loura L. M. S. How To Tackle the Issues in Free Energy Simulations of Long Amphiphiles Interacting with Lipid Membranes: Convergence and Local Membrane Deformations. J. Phys. Chem. B. 2014;118:3572–3581. doi: 10.1021/jp501622d. [DOI] [PubMed] [Google Scholar]
  50. Coimbra J. T. S. Fernandes P. A. Ramos M. J. Revisiting Partition in Hydrated Bilayer Systems. J. Chem. Theory Comput. 2017;13:2290–2299. doi: 10.1021/acs.jctc.6b01258. [DOI] [PubMed] [Google Scholar]
  51. Hub J. S. de Groot B. L. van der Spoel D. g_wham—A Free Weighted Histogram Analysis Implementation Including Robust Error and Autocorrelation Estimates. J. Chem. Theory Comput. 2010;6:3713–3720. doi: 10.1021/ct100494z. [DOI] [Google Scholar]
  52. Jämbeck J. P. M. Lyubartsev A. P. Implicit inclusion of atomic polarization in modeling of partitioning between water and lipid bilayers. Phys. Chem. Chem. Phys. 2013;15:4677–4686. doi: 10.1039/C3CP44472D. [DOI] [PubMed] [Google Scholar]
  53. MacCallum J. L. Bennett W. F. D. Tieleman D. P. Distribution of Amino Acids in a Lipid Bilayer from Computer Simulations. Biophys. J. 2008;94:3393–3404. doi: 10.1529/biophysj.107.112805. [DOI] [PMC free article] [PubMed] [Google Scholar]
  54. Neale C. Bennett W. F. D. Tieleman D. P. Pomès R. Statistical convergence of equilibrium properties in simulations of molecular solutes embedded in lipid bilayers. J. Chem. Theory Comput. 2011;7:4175–4188. doi: 10.1021/ct200316w. [DOI] [PubMed] [Google Scholar]
  55. Orsi M. Essex J. W. Permeability of drugs and hormones through a lipid bilayer: insights from dual-resolution molecular dynamics. Soft Matter. 2010;6:3797–3808. doi: 10.1039/C0SM00136H. [DOI] [Google Scholar]
  56. Lee C. T. Comer J. Herndon C. Leung N. Pavlova A. V Swift R. Tung C. Rowley C. N. Amaro R. E. Chipot C. Wang Y. Gumbart J. C. Simulation-Based Approaches for Determining Membrane Permeability of Small Compounds. J. Chem. Inf. Model. 2016;56:721–733. doi: 10.1021/acs.jcim.6b00022. [DOI] [PMC free article] [PubMed] [Google Scholar]
  57. Swift R. V. Amaro R. E. Back to the Future: Can Physical Models of Passive Membrane Permeability Help Reduce Drug Candidate Attrition and Move Us Beyond QSPR? Chem. Biol. Drug Des. 2013;81:61–71. doi: 10.1111/cbdd.12074. [DOI] [PMC free article] [PubMed] [Google Scholar]
  58. Gasbarri C. Angelini G. Fontana A. De Maria P. Siani G. Giannicchi I. Cort A. D. Kinetics of demetallation of a zinc–salophen complex into liposomes. Biochim. Biophys. Acta. 2012;1818:747–752. doi: 10.1016/j.bbamem.2011.10.014. [DOI] [PubMed] [Google Scholar]
  59. Consiglio G. Pietro Oliveri I. Failla S. Di Bella S. Supramolecular Aggregates of Defined Stereochemical Scaffolds: Aggregation/Deaggregation in Schiff-Base Zinc(II) Complexes Derived from Enantiopure trans-1,2-Diaminocyclohexane. Inorg. Chem. 2016;55:10320–10328. doi: 10.1021/acs.inorgchem.6b01580. [DOI] [PubMed] [Google Scholar]
  60. Hui J. K.-H. MacLachlan M. J. Fibrous aggregates from dinuclear zinc(ii) salphen complexes. Dalton Trans. 2010;39:7310–7319. doi: 10.1039/C0DT00234H. [DOI] [PubMed] [Google Scholar]
  61. Chen L. Chen J. Zhou G. Wang Y. Xu C. Wang X. Molecular Dynamics Simulations of the Permeation of Bisphenol A and Pore Formation in a Lipid Membrane. Sci. Rep. 2016;6:33399. doi: 10.1038/srep33399. [DOI] [PMC free article] [PubMed] [Google Scholar]
  62. Cramariuc O. Rog T. Javanainen M. Monticelli L. Polishchuk A. V. Vattulainen I. Mechanism for translocation of fluoroquinolones across lipid membranes. Biochim. Biophys. Acta. 2012;1818:2563–2571. doi: 10.1016/j.bbamem.2012.05.027. [DOI] [PubMed] [Google Scholar]
  63. Inacio R. Barlow D. Kong X. Keeble J. Jones S. A. Investigating how the attributes of self-associated drug complexes influence the passive transport of molecules through biological membranes. Eur. J. Pharm. Biopharm. 2016;102:214–222. doi: 10.1016/j.ejpb.2016.03.002. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

RA-008-C8RA03602K-s001
RA-008-C8RA03602K-s001.pdf (800.5KB, pdf)

Articles from RSC Advances are provided here courtesy of Royal Society of Chemistry

RESOURCES