Principal component analysis of hybrid functional and vector data

Abstract

We propose a practical principal component analysis (PCA) framework that provides a nonparametric means of simultaneously reducing the dimensions of and modeling functional and vector (multivariate) data. We first introduce a Hilbert space that combines functional and vector objects as a single hybrid object. The framework, termed a PCA of hybrid functional and vector data (HFV-PCA), is then based on the eigen-decomposition of a covariance operator that captures simultaneous variations of functional and vector data in the new space. This approach leads to interpretable principal components that have the same structure as each observation and a single set of scores that serves well as a low-dimensional proxy for hybrid functional and vector data. To support practical application of HFV-PCA, the explicit relationship between the hybrid PC decomposition and the functional and vector PC decompositions is established, leading to a simple and robust estimation scheme where components of HFV-PCA are calculated using the components estimated from the existing functional and classical PCA methods. This estimation strategy allows flexible incorporation of sparse and irregular functional data as well as multivariate functional data. We derive the consistency results and asymptotic convergence rates for the proposed estimators. We demonstrate the efficacy of the method through simulations and analysis of renal imaging data.

1 |. INTRODUCTION

Functional data analysis aims to study various time-dynamic processes that are becoming increasingly prevalent with recent advances in data collection techniques. The crux of functional data analysis is to treat each observed process as a realization of a continuous random function defined over a time or space domain. The inherent smoothness and infinite-dimensionality of functional data enable leveraging their rich and dynamic structure (e.g., derivatives, complex covariance structures, etc.), but at the same time pose unique challenges in their analysis and modeling.

Functional principal component analysis (FPCA) is a key technique that facilitates analysis of functional data, by providing a simple and systematic means of reducing the dimensionality of random functions, while preserving most of the original variability in the data. There is an extensive literature on FPCA, encompassing various types and structures of functional data. Early work on the basic principal of FPCA includes those of Besse and Ramsay¹ and Castro et al.² Subsequently, Rice and Silverman³ and Silverman⁴ proposed a smoothed FPCA based on roughness penalty for dense and regular functional data. For functional data observed on irregular and/or sparse grids, Shi et al,⁵ James et al,⁶ and Rice and Wu⁷ developed a mixed-effects model framework for FPCA, and Staniswalis and Lee⁸ and Yao et al⁹ proposed a local polynomial kernel smoothing approach to estimate the covariance function and subsequently derive the functional principal components (PCs). Theoretical and asymptotic properties of the classical FPCA have been extensively studied in Hall and Hosseini-Nasab,¹⁰ Hall et al,¹¹ and Li and Hsing.¹²

FPCA methods have been extended to functional data with more sophisticated structures. Related work includes, but not limited to: Zhou et al¹³ on paired sparse functional data; Di et al,¹⁴ Greven et al,¹⁵ and Chen and Müller¹⁶ on dependent/repeated functional data; Zhou et al,¹⁷ Staicu et al,¹⁸ Liu et al,¹⁹ and Kuenzer et al²⁰ for spatially correlated functional data; and Zipunnikov et al,²¹ Zhou and Pan,²² and Chen and Jiang²³ on multidimensional functional data. Recently, a series of FPCA methods has been developed for multivariate functional data, where multiple functions are collected for each experimental unit. Jacques and Preda²⁴ and Chiou et al²⁵ developed a multivariate FPCA (MFPCA) method that characterizes simultaneous variations of multiple functions based on a normalized covariance operator. Happ and Greven²⁶ proposed a MFPCA approach that can be flexibly applied to multiple functions observed on different dimensional domains.

All the aforementioned works focus on the principal component analysis (PCA) applied to a single data modality: random functions. With rapid advances in data collection technology, more and more clinical studies and medical devices are becoming capable of collecting multiple data modalities for a sample of subjects or experimental units. In this article, we propose a practical PCA framework for modeling the two data modalities that are frequently collected on each experimental unit in modern clinical studies: functional and vector (multivariate) data. This research is motivated by the renal study at Emory University that aims to identify and understand the co-varying patterns of renogram curves and variables that provide further insights into underlying physiological mechanisms of renal obstruction (obstruction to urine drainage from a kidney). Herein, renogram curves are time activity curves of the uptake and excretion of a gamma emitting tracer by the kidneys, and renogram variables consist of pharmacokinetic parameters of diuresis renography as well as other clinical and demographic factors of the kidneys. Each kidney has two renogram curves (baseline and post-furosemide) and 18 renogram variables, which, respectively, represent multivariate functional data and 18-dimensional vector data. To address the goal of the study, a PCA framework that can characterize simultaneous variations of functional and vector data would be desirable, but has been lacking in the literature.

One possible approach is to perform separate FPCA/MFPCA and classical PCA²⁷ on functional and vector data, respectively. However, the pairwise correlations between the resulting two sets of PC scores (one from FPCA/MFPCA and one from classical PCA) are often nonnegligible, which can lead to multicollinearity issues in subsequent analyses, including PC regression. For instance, nonnegligible cross-correlations between the first three PC scores obtained from MFPCA on two renogram curves and those obtained from PCA on renogram variables exist in the Emory renal study data—see Figure S1. Furthermore, while the two set of PCs capture the dominant variations within respective modes of data, they fail to incorporate the directions that represent maximal joint variability between functional and vector data, resulting in information loss. Alternatively, one can apply the simple approach proposed by Ramsay and Silverman²⁸ that involves presmoothing the functional data using orthogonal basis functions, concatenating the resulting basis coefficients with the vector data to form an augmented vector, and carrying out a classical PCA of the augmented vector data by finding the eigenvalues and eigenvectors of their covariance matrix. This approach, however, encounters difficulties when applied to sparse functional data, on which basis coefficients from the pre-smoothing step are not reliably estimated. Moreover, the method can be unstable as it is sensitive to the choice of the orthogonal basis system used for pre-smoothing.

In contrast, our PCA framework is able to capture and represent the dominant modes of covariation between and within functional and vector objects, providing an efficient nonparametric means of simultaneously modeling the two disparate modes of data. The core strategy is to introduce a Hilbert space that combines functional and vector objects as a single hybrid object, and admits a covariance operator which, by design, characterizes the co-varying structure of functional and vector data. The proposed PCA for hybrid functional and vector data (HFV-PCA) is then based on the eigen-analysis of this new covariance operator and has the following key advantages. First, it produces interpretable PCs that retain maximal variability in the data and have the same structure as each observation. Second, it produces a single set of uncorrelated PC scores which serve well as a low-dimensional proxy for hybrid functional and vector data.

A challenging aspect of the proposed HFV-PCA is performing reliable estimation and eigen-analysis of the covariance operator of hybrid data. Given that this covariance operator consists of cross-covariance functions between functional and vector parts, it is not straightforward to apply or extend the widely used techniques for estimating covariance functions of a single data mode, such as empirical estimation,²⁸ local polynomial kernel smoothing,^9,25 and penalized splines.²⁹ Moreover, a dataset consisting of multiple functions that are measured in different units or have quite different domains poses additional problems to local polynomial smoothing for covariance estimation. To this end, we formulate the hybrid object as a multi-dimensional stochastic process and derive the explicit forms of its covariance operator and PC decomposition that are amenable to practical estimation strategy and rigorous asymptotic analysis. Specifically, using these explicit representations, we establish a theoretical relationship between the hybrid PC decomposition and the functional and vector PC decompositions, and exploit this relationship to derive a practical estimation scheme where components of HFV-PCA are computed using those estimated from the existing FPCA/MFPCA and classical PCA methods. This scheme allows a flexible incorporation of sparse, irregular, and error-prone functional data as well as multivariate functional data, which cannot be readily handled under Ramsay and Silverman’s²⁸ framework. Such an estimation strategy based on the relationship among PC decompositions of different/heterogeneous data modes emerges as a natural extension of the estimation strategy of Happ and Greven²⁶ which combines components of single/homogeneous modes (univariate functions) to estimate those of an integrated data object (multivariate function). The consistency and convergence rates of the proposed estimators are investigated and presented under some mild regularity conditions.

The remainder of the article is organized as follows. In Section 2, we first briefly review the existing PCA and FPCA methods for vector and functional data, respectively. We then introduce a Hilbert space that combines functional and vector objects as a single hybrid object, derive its covariance operator, and establish the theoretical basis for HFV-PCA. This section also presents the estimation scheme where components of HFV-PCA are computed using the components estimated from the existing functional and classical PCA method, and studies the asymptotic properties of the proposed estimators. In Section 3, we conduct simulation studies to evaluate the performance of the proposed approaches. The application of our methods to the Emory renal study is described in Section 4. Concluding remarks are in Section 5. Detailed proofs of the theorems are presented in Appendix S1.

2 |. METHODS

2.1 |. Review of PCA and FPCA

In this section, we briefly review the classical PCA for vector (multivariate) data and FPCA for functional data. Firstly, let X = [X₁, …, X_p]^T denote a p-dimensional vector (multivariate) data in ${\mathbb{R}}^p$. We assume that X is a random vector with finite first two moments and equipped with the Euclidean inner product and norm; that is, for v₁ = [v₁₁, …, v_1p]^T and v₂ = [v₂₁, …, v_2p]^T in ${\mathbb{R}}^p$, $\langle {\mathbf{v}}_{\mathbf{1}},{\mathbf{v}}_{\mathbf{2}}\rangle ={\mathbf{v}}_{\mathbf{1}}^T{\mathbf{v}}_{\mathbf{2}}={\sum }_{r=1}^p{v}_{1r}{v}_{2r}$, and $\Vert {\mathbf{v}}_1\Vert ={\langle {\mathbf{v}}_1,{\mathbf{v}}_1\rangle }^{1/2}={\left({\sum }_{r=1}^p{v}_{1r}^2\right)}^{1/2}$. The classical PCA²⁷ is commonly used to reduce the dimension of X by projecting it onto the space spanned by the first J (< p) vector $\text{PCs}—{\mathbf{w}}_1,\dots ,{\mathbf{w}}_J\in {\mathbb{R}}^p$—that preserve most of the variability in the original vector data. Herein, the first vector PC, w₁, is defined as a direction that maximizes the variance of the projected data. The second vector PC, w₂, identifies the second largest source of variation in the data, while being orthogonal to w₁. The subsequent jth vector PC, w_j, is defined in a similar manner as a direction that maximizes the variance among all directions orthogonal to previous j − 1 vector PCs.

Assume μ_x = E(X) = 0 without loss of generality (WLOG). One mathematical result important for both the theory and implementation of PCA is that vector PCs are equivalent to the orthonormal eigenvectors of the covariance matrix of X. Specifically, let C_x = E(XX^T) denote the covariance matrix, whose eigen-decomposition is given as C_xw_j = κ_jw_j, j = 1, …, p. Here, κ_j is the jth eigenvalue of C_x, and w_j = [w_j1, …, w_jp]^T is the corresponding eigenvector, or equivalently, the jth vector PC. This result leads to the following truncated vector PC decomposition

$$\mathbf{X}\approx {\mathbf{X}}^{[J]}=W^T\mathbf{\gamma }=\sum _{j=1}^J{\gamma }_j{w}_j,\text{or equivalently,}{X}_r^{[J]}=\sum _{j=1}^J{\gamma }_j{w}_{jr},r=1,\dots ,p.$$ (1)

where J (< p) is chosen to explain most variability in X, and W = [w₁, …, w_J]^T is the J × p matrix whose columns are the first J vector PCs, and γ_j = X^Tw_j are uncorrelated vector PC scores with E(γ_j) = 0 and Var(γ_j) = κ_j. The J-dimensional score vector γ = [γ₁, …, γ_J]^T is often used as a lower-dimensional representation of the original data X. Note that κ₁ ≥ κ₂ ≥ … ≥ κ_J > 0, which reiterates the fact that the first vector PC w₁ captures the largest amount of variance in the data, and the subsequent PCs capture successively smaller fractions of this variance. In practice, vector PCs and eigenvalues can be estimated based on the eigen-decomposition of the sample covariance matrix of the observed vector data X_i (i = 1, …, n); that is, ${\widehat{C}}_x{\widehat{\mathbf{w}}}_j={\widehat{\kappa }}_j{\widehat{\mathbf{w}}}_j$ (j = 1, …, J), where ${\widehat{C}}_x={(n-1)}^{-1}{\sum }_{i=1}^n\left({\mathbf{X}}_i-{\widehat{\mathit{\mu }}}_x\right){\left({\mathbf{X}}_i-{\widehat{\mathit{\mu }}}_x\right)}^T$ with ${\widehat{\mathit{\mu }}}_x=n^{-1}{\sum }_{i=1}^n{\mathbf{X}}_i$. The jth vector PC score of ith subject can be estimated as ${\widehat{\gamma }}_{ij}={\left({\mathbf{X}}_i-{\widehat{\mathit{\mu }}}_x\right)}^T{\widehat{\mathbf{w}}}_j$.

We now move on to the FPCA which extends the idea of the classic PCA to functional data. Let {Y^(k)}_{k=1, …, K} be a collection of random functions defined on respective compact domains ${\mathcal{T}}_k\in \mathbb{R}$; that is, $Y^{(k)}:{\mathcal{T}}_k\to \mathbb{R}$. Assume that each Y^(k) is in $L^2\left({\mathcal{T}}_k\right)$, a Hilbert space of square integrable functions with respect to Lebesgue measure dt_k on ${\mathcal{T}}_k$. Write Y = (Y⁽¹⁾, …, Y^(K)) as a multivariate functional object that belongs to $\mathcal{F}=L^2\left({\mathcal{T}}_1\right)\times \dots \times L^2\left({\mathcal{T}}_K\right)$—a cartesian product of individual $L^2\left({\mathcal{T}}_k\right)$ spaces. Note that if K = 1, Y reduces to a univariate functional object. The inner product of $f_1=\left(f_1^{(1)},\dots ,f_1^{(K)}\right)$ and $f_2=\left(f_2^{(1)},\dots ,f_2^{(K)}\right)$ in $\mathcal{F}$ is defined as ${\langle f_1,f_2\rangle }_{\mathcal{F}}={\sum }_{k=1}^K{\int }_{{\mathcal{T}}_k}{f}_1^{(k)}\left(t_k\right)f_2^{(k)}\left(t_k\right)d{t}_k$ with norm $\Vert f_1{\Vert }_{\mathcal{F}}={\langle f_1,f_1\rangle }_{\mathcal{F}}^{1/2}={\left\{{\sum }_{k=1}^K{\int }_{{\tau }_k}{f}_1^{(k)}{\left(t_k\right)}^{2}d{t}_k\right\}}^{1/2}$.

As with the classical PCA, one of the main objectives FPCA is to effectively reduce the dimension of Y, which is inherently infinite-dimensional, by projecting it to a space spanned by the first L functional PCs—${\varphi }_1,\dots ,{\varphi }_L\in \mathcal{F}$—which capture and characterize the dominant modes of variation of functional data. The first functional PC, ${\varphi }_1=\left({\varphi }_1^{(1)},\dots ,{\varphi }_1^{(K)}\right)$, identifies the strongest and most important mode of variation in the random function. The second functional PCs, ${\varphi }_2=\left({\varphi }_2^{(1)},\dots ,{\varphi }_2^{(K)}\right)$, captures the second largest source of variation with the condition that it is orthogonal to φ₁. Similarly, the subsequent functional PCs, ${\varphi }_h=\left({\varphi }_h^{(1)},\dots ,{\varphi }_h^{(K)}\right)$, sequentially capture maximum variability in the functional data while being orthogonal to all previous h – 1 PCs. Note that these functional PCs are orthonormal in the sense that $\langle {\varphi }_h,{\varphi }_l{\rangle }_{\mathcal{F}}={\delta }_{\mathit{hl}}$, with δ_hl = 1 if h = l and δ_hl = 0 if h ≠ l.

Analogous to the classic PCA, functional PCs can be obtained as the eigenfunctions of the covariance operator, which extends the concept of the covariance matrix C_x to a space of square integrable functions $\mathcal{F}$. Specifically, denote the covariance operator of univariate/multivariate functional data Y as $C_y:\mathcal{F}\to \mathcal{F}$ given by ${\left(C_{y}f\right)}^{(k)}\left(t_k\right)={\sum }_{u=1}^K{\int }_{{\tau }_u}{\sigma }_y^{(uk)}\left(s_u,t_k\right)f^{(u)}\left(s_u\right)d{s}_u$, where ${\sigma }_y^{(uk)}\left(s_u,t_k\right)=\mathrm{Cov}\left\{Y^{(u)}\left(s_u\right),Y^{(k)}\left(t_k\right)\right\}$. By the Hilbert-Schmidt theorem,³⁰ this operator satisfies C_Yϕ_h = τ_hϕ_h, $h\in \mathbb{N}$, where τ₁ ≥ τ₂ ≥ … ≥ 0 are the eigenvalues of C_y, and ϕ₁, ϕ₂, … are the corresponding orthonormal eigenfunctions (i.e., functional PCs). Then assuming μ_y = E(Y) = 0, WLOG, the FPCA/MFPCA is based on the following truncated functional PC decomposition, or equivalently, the truncated Karhunen-Loéve expansion:^25,26,31

$$Y\approx Y^{[L]}=\sum _{h=1}^L{\eta }_h{\varphi }_h,\text{i.e.,}{Y}^{[L](k)}\left(t_k\right)=\sum _{h=1}^L{\eta }_h{\varphi }_h^{(k)}\left(t_k\right),t_k\in {\mathcal{T}}_k,k=1,\dots ,K,$$ (2)

where L is chosen to explain most variability in Y, and ${\eta }_h={\langle Y,{\varphi }_h\rangle }_{\mathcal{F}}$ are uncorrelated functional PC scores with mean zero and variance τ_h. The L-dimensional score vector η = [η₁, …, η_L]^T represents functional data Y in the most parsimonious way, in the sense that corresponding functional PCs explain more variation than any other basis expansion given a fixed number of basis functions.²²

Let Y_i (i = 1, …, n) denote observed univariate/multivariate functional data. Different methods can be employed to estimate the FPCA components—τ_h, ϕ_h and η_ih—depending on the type of functional data. For univariate functional data (i.e., $Y_i\equiv Y_i^{(1)}$) observed on a dense regular grid, the mean and covariance functions can be first consistently estimated using the method of moments:² ${\widehat{\mu }}_y(t)=n^{-1}{\sum }_{i=1}^n{Y}_i(t)$ and ${\widehat{\sigma }}_y(s,t)={(n-1)}^{-1}{\sum }_{i=1}^n\left\{Y_i(s)-{\widehat{\mu }}_y(s)\right\}\{Y_i(t)-{\widehat{\mu }}_y(t)\}$. Then, eigenvalues and eigenfunctions (functional PCs) can be estimated by solving the eigen-equation ${\int }_{\mathcal{T}}{\widehat{\sigma }}_y(s,t){\widehat{\varphi }}_h(t)dt={\widehat{\tau }}_h{\widehat{\varphi }}_h(s)$, where the integral can be approximated numerically by a quadrature rule. Finally, the functional PC scores can be estimated by numerical integration: ${\widehat{\eta }}_{ih}={\int }_{\mathcal{T}}\left\{Y_i(t)-{\widehat{\mu }}_y(t)\right\}{\widehat{\varphi }}_h(t)dt$. For univariate functional data observed on a sparse and/or irregular grid, we can take the following steps:⁹ (i) estimate the mean function using a local linear smoother that aggregates data from all observations; (ii) compute the sample raw covariance by aggregating raw covariances of pairwise time points from each functional observation; (iii) estimate the covariance function by smoothing the off-diagonal elements of the sample raw covariance via a local weighted bilinear smoother; (iv) perform eigen-analysis on the smoothed covariance to obtain the estimated eigenfunctions and eigenvalues; and (v) apply principal analysis conditional expectation algorithm to estimate the functional PC scores.

For multivariate functional data observed on a common domain, Chiou et al’s²⁵ MFPCA method can be employed. In short, this approach applies a local linear regression and local linear plane to, respectively, estimate the mean and covariance functions of each multivariate component Y^(k), k = 1, … ,K, and fits a local linear plane to estimate the cross-covariance function across multivariate components. Then, eigenvalues and eigenfunctions can be estimated by solving the eigen-equation that combines the covariance and cross-covariance functions. Finally, the functional PC scores can be obtained as weighted least squares estimates derived from a normalized Karhunen-Loéve expansion. For multivariate functional data observed on possibly different (dimensional) domains, one can employ Happ and Greven’s²⁶ method to estimate the FPCA components separately for each multivariate component using existing univariate methods (see previous paragraph) and then combine them in a way that produces consistent estimates for the MFPCA components.

2.2 |. Theoretical foundation for HFV-PCA

We first establish the theoretical foundation of the proposed HFV-PCA framework that captures and characterizes the dominant modes of variation within and between the random functional object Y and random vector X. The first step is to formulate a hybrid functional and vector random object, Z = (Y, X), which combines Y and X into an ordered pair belonging to $\mathcal{H}=\mathcal{F}\times {\mathbb{R}}^p$. We define the inner product between any two hybrid objects, h₁ = (f₁, v₁) and h₂ = (f₂, v₂), as

$${\langle {\mathbf{h}}_1,{\mathbf{h}}_2\rangle }_{\mathcal{H}}={\langle f_1,f_2\rangle }_{\mathcal{F}}+w\langle {\mathbf{v}}_{\mathbf{1}},{\mathbf{v}}_{\mathbf{2}}\rangle =\sum _{k=1}^K{\int }_{{\mathcal{T}}_k}{f}_1^{(k)}\left(t_k\right)f_2^{(k)}\left(t_k\right)d{t}_k+\omega \sum _{r=1}^p{v}_{1r}{v}_{2r},$$ (3)

with norm $\Vert ·{\Vert }_{\mathcal{H}}={\langle .,.\rangle }_{\mathcal{H}}^{1/2}·\omega$ is a positive weight that needs to be prespecified or estimated. It is mainly used to take into account heterogeneity between functional and vector parts in terms of measurement scale and/or amount of variation.²⁸ Its application will be discussed in detail in Section 2.5. WLOG and for the clarity of illustration, all the following theoretical results will be derived for ω = 1. The results remain valid for any positive weights.

The space $\mathcal{H}$ equipped with the inner product ${\langle ·,·\rangle }_{\mathcal{H}}$ defined as (3) is a separable Hilbert space,³² in which, given $\text{E}\parallel \mathbf{Z}{\parallel }_{\mathcal{H}}^2<\infty$, we can readily define the mean and covariance operator of Z as μ = E(Z) and $\mathcal{K}=\text{E}\{(\mathbf{Z}-\mu )\otimes (\mathbf{Z}-\mu )\}$, respectively, where the latter is a mapping $\mathcal{K}:\mathcal{H}\to \mathcal{H}$ induced by the tensor product operator ⊗. The theoretical foundation of HFV-PCA is established based on the covariance operator $\mathcal{K}$, which admits the following the eigen-decomposition (e.g., theorem 7.2.6 in Hsing and Eubank³⁰):

$$\mathcal{K}=\sum _{m=1}^{\infty }{\lambda }_m\left({\xi }_m\otimes {\xi }_m\right),$$ (4)

where ${\left\{{\lambda }_m\right\}}_{m=1}^{\infty }$ is a set of nonnegative and nondecreasing eigenvalues, and ${\left\{{\xi }_m\right\}}_{m=1}^{\infty }$ is a set of complete orthonormal basis of eigenfunctions in $\mathcal{H}$ satisfying $\langle {\xi }_m,{\xi }_n{\rangle }_{\mathcal{H}}={\delta }_{mn}$. The eigen-decomposition in (4) leads to the following hybrid PC decomposition (e.g., theorem 7.2.7 in Hsing and Eubank³⁰)

$$\mathbf{Z}=\mathit{\mu }+\sum _{m=1}^{\infty }{\rho }_m{\mathit{\xi }}_m,$$ (5)

with probability 1. This hybrid PC decomposition is the foundation for HFV-PCA. The eigenvalues λ_m, $m\in \mathbb{N}$, quantifies the amount of variability in Z explained by the corresponding eigenfunctions ξ_m, or equivalently, hybrid PCs. The first hybrid PC, ξ₁, identifies the strongest and most important mode of the joint variation of functional and vector parts. The subsequent PCs capture successively smaller fractions of this variation. The random variables ${\rho }_m=\langle \mathbf{Z},{\xi }_m{\rangle }_{\mathcal{H}}$ are uncorrelated with mean zero and variance λ_m and are called the hybrid PC scores.

2.3 |. Stochastic process modeling for practical implementation of HFV-PCA

Although the hybrid PC decomposition presented in (5) lays foundation for HFV-PCA, the formulation is rather abstract for practical implementation. Thus, in this section, we rebuild our framework under the perspective that the hybrid random variable Z is a multi-dimensional stochastic process with respect to a multi-dimensional argument $\mathbf{t}={\left[t_1,\dots t_k\right]}^T\in \mathcal{T}={\mathcal{T}}_1\times \dots \times {\mathcal{T}}_K$, and derive the explicit forms of the covariance operator and Karhunen-Loéve expansion³³ that are amenable to simple estimation and rigorous asymptotic analysis.

Let $\mathbf{Z}[\mathbf{t}]={[Y(\mathbf{t}),\mathbf{X}]}^T={\left[Y^{(1)}\left(t_1\right),\dots ,Y^{(K)}\left(t_K\right),X_1,\dots ,X_p\right]}^T\in {\mathbb{R}}^{K+p}$ for $\mathbf{t}\in \mathcal{T}$. To make the hybrid PC decomposition (5) more amenable to practical implementations, we treat $\{\mathbf{Z}[\mathbf{t}]:\mathbf{t}\in \mathcal{T}\}$ as a (K + p)-dimensional stochastic process where only its first K elements (functional part) depends on the argument t. The mean function of Z[t] is μ[t] = E(Z[t]) = [EY(t),EX]^T, which we assume to equal 0 WLOG; that is, both functional and vector data are centered in advance.

For $s_u\in {\mathcal{T}}_u,t_k\in {\mathcal{T}}_k$, u, k = 1, …, K and q, r = 1, …, p, we define the following three covariance kernels: (1) ${\sigma }_y^{(uk)}\left(s_u,t_k\right)=\mathrm{Cov}\left\{Y^{(u)}\left(s_u\right),Y^{(k)}\left(t_k\right)\right\}$ which denotes the covariance between two functions (if u = k, this is a covariance function of Y^(k)); (2) σ_x(q, r) = Cov(X_q, X_r) which denotes the covariance between two vector elements (if q = r, this is a variance of X_r); and (3) ${\sigma }_{yx}^{(k)}\left(t_k,r\right)=\mathrm{Cov}\left\{Y^{(k)}\left(t_k\right),X_r\right\}$ which represents the cross-covariance function between the kth function and rth element of a vector. Further note that: ${\sigma }_y(·,·)\in \mathcal{F}\times \mathcal{F},{\sigma }_y^{(k)}\left(·,t_k\right)\in \mathcal{F}$ for fixed $t_k,{\sigma }_{yx}^{(k)}\left(t_k,·\right)\in {\mathbb{R}}^p$ for fixed $t_k,{\sigma }_{yx}(·,r)\in \mathcal{F}$ for fixed $r,{\sigma }_x(r,·)\in {\mathbb{R}}^p$ for fixed r, and σ_x(·, ·) is a p × p covariance matrix of X. We now derive the explicit form of the covariance operator $\mathcal{K}:\mathcal{H}\to \mathcal{H}$ that comprises of σ_y, σ_x, and σ_yx, and characterizes the variation within and between the functional and vector parts. Since $(\mathcal{K}\mathbf{h})[\mathbf{t}]=\{\text{E}(\mathbf{Z}\otimes \mathbf{Z})\mathbf{h}\}[\mathbf{t}]=\text{E(}{\langle \mathbf{Z},h\rangle }_{\mathcal{H}}\left(\mathbf{Z}[\mathbf{t}]\right)$ for any $\mathbf{h}=(f,\mathbf{v})\in \mathcal{H}$, elements of the functional and vector parts of $(\mathcal{K}\mathbf{h})[\mathbf{t}]={\left[{(\mathcal{K}\mathbf{h})}^{(1)}\left(t_1\right),\dots {(\mathcal{K}\mathbf{h})}^{(K)}\left(t_K\right),{(\mathcal{K}\mathbf{h})}_1,\dots ,{(\mathcal{K}\mathbf{h})}_p\right]}^T\in {\mathbb{R}}^{K+p}$ can be derived as

$${(\mathcal{K}\mathbf{h})}^{(k)}\left(t_k\right)=\sum _{u=1}^K{\int }_{{\mathcal{T}}_{{}_u}}{\sigma }_y^{(uk)}\left(s_u,t_k\right)f^{(u)}\left(s_u\right)d{s}_u+\sum _{r=1}^p{\sigma }_{yx}^{(k)}\left(t_k,r\right)v_r={\langle {\text{Σ}}^{(k)}\left[t_k,·\right],\mathbf{h}\rangle }_{\mathcal{H}}$$

$${(\mathcal{K}\mathbf{h})}_r=\sum _{u=1}^K{\int }_{{\mathcal{T}}_{{}_u}}{\sigma }_{yx}^{(u)}\left(s_u,r\right)f^{(u)}\left(s_u\right)d{s}_u+\sum _{q=1}^p{\sigma }_x(q,r)v_q={\langle \text{Σ}[·,r],\mathbf{h}\rangle }_{\mathcal{H}},$$ (6)

respectively, for k = 1, …, K and r = 1, …, p, where ${\text{Σ}}^{(k)}\left[t_k,·\right]=\left({\sigma }_y^{(k)}\left(·,t_k\right),{\sigma }_{yx}^{(k)}\left(t_k,·\right)\right)$ and Σ[·, r] = (σ_yx(·, r), σ_x(r, ·)) are elements in $\mathcal{H}$.

The formulation (6) allows us to specify explicit boundedness and continuity conditions that the covariance kernels (σ_y, σ_yx, and σ_x) should satisfy in order for $\mathcal{K}$ to be a positive self-adjoint compact operator. Specifically, we have the following theorem:

Theorem 1. The covariance operator $\mathcal{K}$ defined in (6) is positive and self-adjoint. Furthermore, suppose σ_y, σ_yx, and σ_x are bounded in the sense that: there exist finite constants C₁, C₂, C₃ and C₄ such that

$$\underset{k=1,\dots ,K}{\max }\underset{t_k\in {\mathcal{T}}_k}{\sup }\Vert {\sigma }_{yx}^{(k)}(·,t_k){\Vert }_{\mathcal{F}}^2=\underset{k=1,\dots ,K}{\max }\underset{t_k\in {\mathcal{T}}_k}{\sup }\sum _{u=1}^K{\int }_{{\mathcal{T}}_{{}_u}}{\sigma }_y^{(uk)}{\left(s_u,t_k\right)}^{2}d{s}_u<C_1,$$

$$\underset{k=1,\dots ,K}{\max }\underset{t_k\in {\mathcal{T}}_k}{\sup }\Vert {\sigma }_{yx}^{(k)}(t_k,.){\Vert }^2=\underset{k=1,\dots ,K}{\max }\underset{t_k\in {\mathcal{T}}_k}{\sup }\sum _{r=1}^p{\sigma }_{yx}^{(k)}{\left(t_k,r\right)}^2<C_2,$$

$$\underset{r=1,\dots ,p}{\max }\Vert {\sigma }_{yx}(·,r){\Vert }_{\mathcal{F}}^2=\underset{r=1,\dots ,p}{\max }\sum _{u=1}^K{\int }_{{\mathcal{T}}_{{}_u}}{\sigma }_{yx}{\left(s_u,r\right)}^{2}d{s}_u<C_3,$$

$$\underset{r=1,\dots ,p}{\max }\Vert {\sigma }_x(·,r){\Vert }^2=\underset{r=1,\dots ,p}{\max }\sum _{q=1}^p{\sigma }_x{(q,r)}^2<C_4.$$

Also suppose σ_y and σ_yx are uniformly continuous in the sense that: for all k, u = 1, …, K, r = 1, …, p and ϵ > 0, there exist δ^(uk), ${\delta }_r^{(k)}>0$ such that

$$\begin{gathered} \left|t_k-t_k^{\ast }\right|<{\delta }^{(uk)}\Rightarrow \left|{\sigma }_y^{(uk)}\left(s_u,t_k\right)-{\sigma }_y^{(uk)}\left(s_u,t_k^{\ast }\right)\right|<ϵ\text{for all}{s}_u\in {\mathcal{T}}_u \\ \left|t_k-t_k^{\ast }\right|<{\delta }_r^{(k)}\Rightarrow \left|{\sigma }_{yx}^{(k)}\left(t_k,r\right)-{\sigma }_{yx}^{(k)}\left(t_k^{\ast },r\right)\right|<ϵ. \end{gathered}$$

Then, $\mathcal{K}$ is a compact operator.

By the Hilbert-Schmidt theorem (e.g., theorem 4.2.4 in Hsing and Eubank³⁰), it follows that there exists a complete orthonormal system of eigenfunctions ${\left\{{\xi }_m=\left({\psi }_m,{\mathit{\theta }}_m\right)\right\}}_{m\in \mathbb{N}}$ of $\mathcal{K}$ such that $\left(\mathcal{K}{\xi }_m\right)[\mathbf{t}]={\lambda }_m{\xi }_m[\mathbf{t}]$, where ${\left\{{\lambda }_m\right\}}_{m\in \mathbb{N}}$ is the corresponding sequence of eigenvalues that goes to zero as m → ∞ and λ₁ ≥ λ₂ ≥ … ≥ 0. Moreover, for any $\mathbf{h}\in \mathcal{H}$, we have $(\mathcal{K}\mathbf{h})[\mathbf{t}]={\sum }_{m=1}^{\infty }{\lambda }_m\langle \mathbf{h},{\xi }_m{\rangle }_{\mathcal{H}}{\xi }_m[\mathbf{t}]$, which is equivalent to the eigen-decomposition presented in (4). For future applications, we derive the following element-wise representations of the Hilbert-Schmidt theorem:

$${\left(\mathcal{K}{\xi }_m\right)}^{(k)}\left(t_k\right)=\sum _{u=1}^K{\int }_{{\mathcal{T}}_{{}_u}}{\sigma }_y^{(uk)}\left(s_u,t_k\right){\psi }_m^{(u)}\left(s_u\right)d{s}_u+\sum _{r=1}^p{\sigma }_{yx}^{(k)}\left(t_k,r\right){\theta }_{mr}={\lambda }_m{\psi }_m^{(k)}\left(t_k\right),$$

$${\left(\mathcal{K}{\xi }_m\right)}_r=\sum _{u=1}^K{\int }_{{\mathcal{T}}_{{}_u}}{\sigma }_{yx}^{(u)}\left(s_u,r\right){\psi }_m^{(u)}\left(s_u\right)d{s}_u+\sum _{q=1}^p{\sigma }_x\left(q,r\right){\theta }_{mq}={\lambda }_m{\theta }_{mr},$$

$${(\mathcal{K}\mathbf{h})}^{(k)}\left(t_k\right)=\sum _{u=1}^K{\int }_{{\mathcal{T}}_{{}_u}}{\sigma }_y^{(uk)}\left(s_u,t_k\right)f^{(u)}\left(s_u\right)d{s}_u+\sum _{r=1}^p{\sigma }_{yx}^{(k)}\left(t_k,r\right)v_r=\sum _{m=1}^{\infty }{\lambda }_m\mathbf{h},{\xi }_m{}_{\mathcal{H}}{\psi }_m^{(k)}\left(t_k\right),$$

$${(\mathcal{K}\mathbf{h})}_r=\sum _{u=1}^K{\int }_{{\mathcal{T}}_{{}_u}}{\sigma }_{yx}^{(u)}\left(s_u,r\right)f^{(u)}\left(s_u\right)d{s}_u+\sum _{q=1}^p{\sigma }_x\left(q,r\right)v_q=\sum _{m=1}^{\infty }{\lambda }_m{\langle \mathbf{h},{\xi }_m\rangle }_{\mathcal{H}}{\theta }_{mr},$$

where ${\psi }_m=\left({\psi }_m^{(1)},\dots ,{\psi }_m^{(K)}\right)\in \mathcal{F}$, and ${\theta }_m={\left[{\theta }_{m1},\dots ,{\theta }_{mp}\right]}^T\in {\mathbb{R}}^p$.

Mercer’s theorem³⁴ provides an eigen-decomposition of a symmetric nonnegative definite kernel of an integral operator and serves as a key ingredient in the proof of the Karhunen-Loéve theorem of stochastic processes (e.g., theorem 7.3.5 in Hsing and Eubank³⁰). As such, we introduce the following two theorems which sensibly adapt the Mercer’s and Karhunen-Loéve theorems to our context of hybrid data.

Theorem 2. Under the assumptions of Theorem 1, for k = 1, …, K and s_k, $t_k\in {\mathcal{T}}_k$,

$$Cov\left(Y^{(k)}\left(s_k\right),Y^{(k)}\left(t_k\right)\right)={\sigma }_y^{(kk)}\left(s_k,t_k\right)=\sum _{m=1}^{\infty }{\lambda }_m{\psi }_m^{(k)}\left(s_k\right){\psi }_m^{(k)}\left(t_k\right),$$

where the convergence is absolute and uniform. For r = 1, …, p,

$$Var\left(X_r\right)={\sigma }_x(r,r)=\sum _{m=1}^{\infty }{\lambda }_m{\theta }_{mr}^2,$$

where the convergence is absolute.

Theorem 3. Given Theorem 2, the hybrid random variable Z admits the following representation

$$\mathbf{Z}[\mathbf{t}]=\sum _{m=1}^{\infty }{\rho }_m{\xi }_m[\mathbf{t}],\mathbf{t}\in \mathcal{T},$$ (7)

${\rho }_m=\langle \mathbf{Z},{\xi }_m{\rangle }_{\mathcal{H}}$ with E(ρ_m) = 0 and E(ρ_mρ_n) = λ_mδ_mn, and ξ_m[t] = [ψ_m(t), θ_m]^T. Moreover, we have

$$\underset{M\to \infty }{\lim }\underset{\mathbf{t}\in \mathcal{T}}{\sup }\text{E}\left\{\Vert \mathbf{Z}[\mathbf{t}]-\sum _{m=1}^M{\rho }_m{\xi }_m[\mathbf{t}]{\Vert }^2\right\}=0.$$

The Karhunen-Loéve expansion (7) and the hybrid PC decomposition (5) have essentially the same form and interpretation, though deriving the former has two additional merits. Firstly, it translates the hybrid PC decomposition (5) constructed in an abstract Hilbert space to a more familiar space of mean-square continuous stochastic processes, where we could specify explicit necessary conditions on covariance kernels that are easily comprehensible and convincing. Secondly, it bridges a conceptual and analytical relationship between the hybrid PC decomposition and the usual functional and vector PC decompositions, and such a relationship is crucial for subsequent development of estimation schemes. In practice, the main focus is on deriving the following truncated hybrid PC decomposition (or equivalently, truncated Karhunen-Loéve expansion)

$${\mathbf{Z}}^{[M]}[\mathbf{t}]=\sum _{m=1}^M{\rho }_m{\xi }_m[\mathbf{t}],\mathbf{t}\in \mathcal{T},$$ (8)

where M is a finite positive integer. The first M hybrid PC scores {ρ₁, ρ₂, …, ρ_M} and hybrid PCs {ξ₁, ξ₂, …, ξ_M) are optimal M-dimensional approximations to Z for each M in the sense that (cf, theorem 7.2.8 in Hsing and Eubank³⁰)

$${\left\{{\xi }_m\right\}}_{m=1}^M=\underset{{\left\{{\mathbf{h}}_m\right\}}_{m=1}^M}{\arg \min }\text{E}\Vert \mathbf{Z}-\sum _{m=1}^M{\langle \mathbf{Z},{\mathbf{h}}_m\rangle }_{\mathcal{H}}{\mathbf{h}}_m{\Vert }_{\mathcal{H}},$$

where ${\left\{{\mathbf{h}}_m\right\}}_{m=1}^{\infty }$ is any complete orthogonal system in $\mathcal{H}$.

2.4 |. Relationship between hybrid PC decomposition and functional and vector PC decompositions

Recently, Happ and Greven²⁶ derived an analytical relationship between the PC decompositions of multivariate and univariate functional data based on the theory of integral equations and their augmentations.³⁵ In this section, we extend this approach to our hybrid setting (heterogeneous data modes) to establish the analytical relationship between the truncated hybrid PC decomposition (8) and the truncated functional (2) and vector PC decompositions (1), respectively, derived from the existing FPCA/MFPCA^9,26,28 and classical PCA²⁷ methods.

We begin by approximating the functional and vector parts of a hybrid object Z = (Y,X) with the truncated functional (2) and vector (1) PC decompositions, respectively—that is, $\tilde{\mathbf{Z}}=\left(Y^{[L]},{\mathbf{X}}^{[J]}\right)=\left({\sum }_{h=1}^L{\eta }_h{\varphi }_h,{\sum }_{j=1}^J{\gamma }_j{\mathbf{w}}_j\right)$. Let $\tilde{\mathcal{K}}=\text{E}(\tilde{Z}\otimes \tilde{Z})$ be the covariance operator formulated with the approximated hybrid object $\tilde{\mathbf{Z}}$. Then, for $\mathbf{h}\in \mathcal{H}$, each element of $\tilde{\mathcal{K}}\mathbf{h}$ is

$${(\tilde{\mathcal{K}}\mathbf{h})}^{(k)}\left(t_k\right)=\sum _{u=1}^K{\int }_{{\mathcal{T}}_{{}_u}}{\tilde{\sigma }}_y^{(uk)}\left(s_u,t_k\right)f\left(s_u\right)d{s}_u+\sum _{r=1}^P{\tilde{\sigma }}_{yx}^{(k)}\left(t_k,r\right)v_r,$$

$${(\tilde{\mathcal{K}}\mathbf{h})}_r=\sum _{u=1}^K{\int }_{{\mathcal{T}}_{{}_u}}{\tilde{\sigma }}_{yx}^{(u)}\left(s_u,r\right)f^{(u)}\left(s_u\right)d{s}_u+\sum _{q=1}^P{\tilde{\sigma }}_x\left(q,r\right)v_q,$$

where ${\tilde{\sigma }}_y^{(uk)}\left(s_u,t_k\right)=Cov\left\{Y^{[L](u)}\left(s_u\right),Y^{[L](k)}\left(t_k\right)\right\}$, ${\tilde{\sigma }}_{yx}^{(u)}\left(s_u,r\right)=Cov\left\{Y^{[L](u)}\left(s_u\right),X_r^{[J]}\right\}$ and ${\tilde{\sigma }}_x(q,r)=Cov\left(X_q^{[J]},X_r^{[J]}\right)$ for $S_u\in {\mathcal{T}}_u,t_k\in {\tilde{\mathcal{T}}}_k$, and q, r = 1, …, p. Let ${\tilde{\lambda }}_m$ and ${\tilde{\xi }}_m,m\in \mathbb{N}$, respectively, denote the eigenvalues and eigenfunctions of $\tilde{\mathcal{K}}$. Such an eigen-analysis yields the following approximate truncated hybrid PC decomposition

$${\tilde{\mathbf{Z}}}^{[M]}[\mathbf{t}]=\sum _{m=1}^M{\tilde{\rho }}_m{\tilde{\xi }}_m[\mathbf{t}],\mathbf{t}\in \mathcal{T},$$ (9)

where ${\tilde{\xi }}_m$ and ${\tilde{\rho }}_m=\tilde{\mathbf{Z}},{\tilde{\xi }}_m{}_{\mathcal{H}}$ represent approximate hybrid PCs and scores, respectively. Note that the scores ${\tilde{\rho }}_m$ are uncorrelated and have variances equal to ${\tilde{\lambda }}_m$.

In the following theorem, we establish an analytical relationship between the approximate truncated hybrid PC decomposition (9) and the truncated functional and vector PC decompositions–(2) and (1)–based on the integral augmentation approach^26,35 generalized to a hybrid setting.

Theorem 4. Suppose that truncated functional and vector PC decompositions are given as (2) and (1), respectively. Define four matrices that characterize covariances within and between functional and vector PC scores: $V_y={\left\{Cov\left({\eta }_h,{\eta }_l\right)\right\}}_{h=1,\dots ,L}^{l=1,\dots ,L}\in {\mathbb{R}}^{L\times L}$, $V_{yx}={\left\{Cov\left({\eta }_h,{\gamma }_j\right)\right\}}_{h=1,\dots ,L}^{j=1,\dots ,J}\in {\mathbb{R}}^{L\times J}$, $V_{xy}=V_{yx}^T$ and $V_x={\left\{Cov\left({\gamma }_j,{\gamma }_q\right)\right\}}_{j=1,\dots ,J}^{q=1,\dots ,J}\in {\mathbb{R}}^{J\times J}$. Define a (L + J) × (L + J) symmetric and positive semi-definite matrix that contains the above four matrices as blocks

$$V=\left[\begin{array}{cc}{V}_y& V_{yx}\\ V_{xy}& V_{x.}\end{array}\right].$$

Then, for m = 1, …, M with M ≤ L + J, the mth eigenvalue of V, ${\tilde{\lambda }}_m$, is exactly the mth eigenvalue of $\tilde{\mathcal{K}}$. Denote the mth (L + J)-dimensional eigenvector of V as ${\mathbf{e}}_m={\left[{\mathbf{c}}_m^T,{\mathbf{d}}_m^T\right]}^T$, where c_m = [c_m1, …, c_mL]^T denotes the first L elements of e_m, and d_m = [d_m1, …, d_mJ]^T denotes the last J elements of em, Then, functional and vector parts of the mth approximate hybrid PC (eigenfunction of $\tilde{\mathcal{K}}$), ${\tilde{\xi }}_m=\left({\tilde{\psi }}_m,{\tilde{\theta }}_m\right)$, are

$${\tilde{\psi }}_m(\mathbf{t})=\sum _{h=1}^L{c}_{mh}{\varphi }_h(\mathbf{t})\text{and}{\tilde{\theta }}_m=\sum _{j=1}^J{d}_{mj}{\mathbf{w}}_j,$$

respectively. The approximate hybrid PC score is

$${\tilde{\rho }}_m=\sum _{h=1}^L{\eta }_h{c}_{mh}+\sum _{j=1}^J{\gamma }_j{d}_{mj}.$$

In Section 2.6, we will prove that the approximate HFV-PCA components—${\tilde{\lambda }}_m$, ${\tilde{\xi }}_m$ and ${\tilde{\rho }}_m$—converge to the true HFV-PCA components—λ_m, ξ_m, and ρ_m–respectively, for each $m\in \mathbb{N}$ as L → ∞ and J → p, that is, as more functional and vector PCs are used to approximate Z via $\tilde{\mathbf{Z}}$. In other words, the analytic relationship established in Theorem 4 holds between the true truncated hybrid PC decomposition (8) and the functional and vector PC decompositions–(2) and (1)–in an asymptotic sense.

2.5. Estimation

The analytical relationship established in Theorem 4, and the fact that this relationship holds asymptotically for the true truncated hybrid PC decomposition (see Section 2.6), lead to a simple, robust, and comprehensive estimation strategy where HFV-PCA components are estimated using the FPCA/MFPCA and PCA components. Consider a random sample {(Y₁, X₁), …, (Y_n, X_n)} drawn from the joint distribution of (Y, X). The proposed estimation scheme comprises of the following four steps.

1. Perform FPCA/MFPCA on observed functional data Y_i, i = 1, …, n, to estimate functional PCs and PC scores—that is, obtain ${\widehat{\varphi }}_h$ and ${\widehat{\eta }}_{ih}$, h = 1, …, L, where L is a truncation lag determined data-adaptively. Different FPCA/MFPCA techniques can be flexibly chosen in different contexts. Please see the last two paragraphs of Section 2.1 for a summary of FPCA/MFPCA methods that are applicable to four different types of functional data: (i) univariate functional data on a dense and regular grid;² (ii) univariate functional data on a sparese and/or irregular grid;⁹ (iii) multivariate functional data observed on a common domain;²⁵ and (iv) multivariate functional data observed on different (dimensional) domains.²⁶

2. Perform classical PCA²⁷ on observed vector data X_i, i = 1, …, n, to estimate vector PCs and vector PC scores–that is, obtain ${\widehat{\mathbf{w}}}_j$, and ${\widehat{\gamma }}_{ij}$, j = 1, …, J, where J is a truncation lag determined data-adaptively.

3. For each i, create a (L + J)-dimensional vector ${\widehat{\chi }}_i={\left[{\widehat{\eta }}_{i1},\dots ,{\widehat{\eta }}_{iL},{\widehat{\gamma }}_{i1},\dots ,{\widehat{\gamma }}_{iJ}\right]}^T$ that concatenates the functional and vector PC scores, and compute $\widehat{V}={(n-1)}^{-1}{\sum }_{i=1}^n{\widehat{\chi }}_i{\widehat{\chi }}_i^T$ which estimates the (L + J) × (L + J) matrix V of Theorem 4.

4. Perform an eigen-analysis of $\widehat{V}$ to obtain eigenvalues ${\widehat{\lambda }}_m$ and orthonormal eigenvectors ${\widehat{\mathbf{e}}}_m=\left[{\widehat{\mathbf{c}}}_m,{\widehat{\mathbf{d}}}_m\right]$, m = 1, …, M, M ≤ L + J, where M is a truncation lag that is chosen data-adaptively, and ${\widehat{\mathbf{c}}}_m={\left[{\widehat{C}}_{m1},\dots ,{\widehat{C}}_{mL}\right]}^T$ and ${\widehat{\mathbf{d}}}_m={\left[{\widehat{d}}_{m1},\dots ,{\widehat{d}}_{mJ}\right]}^T$ denote the first L and last J elements of ${\widehat{\mathbf{e}}}_m$, respectively.

5. Estimate the functional and vector parts of the mth hybrid PC ξ_m = (ψ_m, θ_m) and mth hybrid PC score of ith observation, respectively, by

   $${\widehat{\psi }}_m(\mathbf{t})=\sum _{h=1}^L{\widehat{c}}_{mh}{\widehat{\varphi }}_h(\mathbf{t}),{\widehat{\theta }}_m=\sum _{j=1}^J{\widehat{d}}_{mj}{\widehat{\mathbf{w}}}_j\text{and}{\widehat{\rho }}_{im}=\sum _{h=1}^J{\widehat{\eta }}_{ih}{\widehat{c}}_{mh}+\sum _{j=1}^J{\widehat{\gamma }}_{ij}{\widehat{d}}_{mj}.$$

Choosing appropriate truncation lags L and J in Steps 1 and 2 is significant as they control how much of the information from the functional and vector parts is used for HFV-PCA. A widely used criterion is the “percentage of variance explained,” which selects L and J as the minimal number of functional and vector PCs that explain 100δ% of the total variability.^27,28 In practice, this can be implemented by setting $L={\min }_l\left\{\left({\sum }_{h=1}^l{\widehat{\tau }}_h/{\sum }_{h=1}^{n-1}{\widehat{\tau }}_h\right)>\delta \right\}$ and $j={\min }_l\left\{\left({\sum }_{q=1}^j{\widehat{\kappa }}_q/{\sum }_{q=1}^{p*}{\widehat{\kappa }}_q\right)>\delta \right\}$, where ${\widehat{\tau }}_h$, and ${\widehat{K}}_j$, respectively, denote eigenvalues of ${\widehat{C}}_y$ and ${\widehat{C}}_x$ (i.e., estimated covariance function of Y and estimated covariance matrix of X), and p* = min(n − 1, p). Note that with L and J determined, the remaining terms $\underset{t\in \mathcal{T}}{\sup }{\sum }_{h=L+1}^{\infty }{\eta }_{ih}{\varphi }_h(t)$ and ${\sum }_{q=J+1}^p{\gamma }_{iq}{\mathbf{w}}_q$ are assumed to be negligible. Prior empirical studies in the context of multivariate functional data suggest that there exists a threshold value of δ, above which functional and vector parts contribute sufficient information to warrant accurate estimation of HFV-PCA, but below which they do not provide enough information to produce reliable estimates.²⁶ As such, our general recommendation is to choose a sufficiently high value of δ (e.g., δ = 0.99) that minimizes the chance of resulting in inaccurate estimations. Note that this does not mean we can simply choose the maximum number of functional and vector PCs, including negligible terms, because this may result in high approximation error coming from having to estimate too many terms (see Section 2.6). Once L and J are selected, an optimal truncation lag, M, of HFV-PCA can be chosen based on the percentage of variance explained—that is, $M=\underset{m}{\min }\left\{\left({\sum }_{u=1}^m{\widehat{\lambda }}_u/{\sum }_{u=1}^{n-1}{\widehat{\lambda }}_u\right)>{\delta }_0\right\}$—such that the leading M hybrid PCs explain 100δ₀% of total variability.

A potential difficulty with HFV-PCA is that elements within and between functional and vector parts often have incompatible units and/or exhibit different amounts of variation. The first task is to account for discrepancies within respective functional and vector parts, if needed. If elements of multivariate functional data $Y_i=\left(Y_i^{(1)},\dots ,Y_i^{(K)}\right)$ are measured in different units or have quite different domains, one can rescale them to have integrated variance of one. If elements of the vector X_i = [X_i1, …, X_ip]^T exhibit different amounts of variation, one can standardize them to have unit variance. The second task is to eliminate the influence of different measurement scales between functional and vector parts. To accomplish this aim, we propose to choose an appropriate weight ω in the inner product (3) that ensures functional and vector parts contribute equal amounts of variation to HFV-PCA. A sensible data-driven approach to choosing an appropriate weight, analogous to the standardization of data prior to PCA, is to set

$$\omega =\frac{{\sum }_{i=1}^n\Vert Y_i-\overline{Y}{\Vert }_{\mathcal{F}}^2}{{\sum }_{i=1}^n\Vert {\mathbf{X}}_i-\overline{\mathbf{X}}{\Vert }^2},$$ (10)

where $\overline{Y}=n^{-1}\left({\sum }_{i=1}^n{Y}_i^{(1)},\dots {\sum }_{i=1}^n{Y}_i^{(K)}\right)$, and $\overline{X}=n^{-1}{\left[{\sum }_{i=1}^n{X}_{i1},\dots ,{\sum }_{1=1}^n{X}_{ip}\right]}^T$ are sample mean function and vector, respectively. In practice, the weighting scheme (10) can be implemented by formulating the hybrid object as Z = (Y, ω^1/2X), whose vector part has been scaled by a factor of ω^1/2, and proceeding with the estimation steps (a) to (e).

2.6 |. Asymptotic results

In this section, we investigate the asymptotic properties of the estimators of HFV-PCA components $\left({\widehat{\lambda }}_m,{\widehat{\psi }}_m,{\widehat{\rho }}_{im}\right)$ derived in Section 2.5. The asymptotic study considers two sources of errors: approximation error and estimation error. The former error stems from the fact that the estimators are derived based on Theorem 4, which delineates the relationship between the approximate truncated hybrid PC decomposition (9) and the truncated functional (2) and vector (1) PC decompositions; that is, the true components of HFV-PCA $\left({\lambda }_m,{\xi }_m,{\rho }_{im}\right)$ are approximated by $\left({\tilde{\lambda }}_m,{\tilde{\xi }}_m,{\tilde{\rho }}_{im}\right)$ derived from $\tilde{\mathcal{K}}$. The latter corresponds to the usual sampling error caused by observing a sample of hybrid objects instead of its true population. Hence, we have the following error decompositions of the proposed estimators:

$$\left|{\lambda }_m-{\widehat{\lambda }}_m\right|=\left|{\lambda }_m-{\tilde{\lambda }}_m\right|+\left|{\tilde{\lambda }}_m-{\widehat{\lambda }}_m\right|$$

$$\Vert {\xi }_m-{\widehat{\xi }}_m{\Vert }_{\mathcal{H}}=\Vert {\xi }_m-{\tilde{\xi }}_m{\Vert }_{\mathcal{H}}+{\tilde{\xi }}_m-{\widehat{\xi }}_m{\Vert }_{\mathcal{H}}$$

$$\left|{\rho }_{im}-{\widehat{\rho }}_{im}\right|=\left|{\rho }_{im}-{\tilde{\rho }}_{im}\right|+\left|{\tilde{\rho }}_{im}-{\widehat{\rho }}_{im}\right|,$$

where the first and second terms on the right-hand of the inequalities represent the approximation errors and estimation errors, respectively.

The following theorem presents the asymptotic behavior of the approximation error. It is important to note that this error only depends on the sample size n through L and J (truncation lags for functional and vector PCs, respectively), which are bounded above by and may increase with n.

Theorem 5. For $m\in \mathbb{N}$, let ${\tilde{\lambda }}_m$ denote the finite-multiplicity eigenvalues of the covariance operator $\tilde{\mathcal{K}}$ associated with $\tilde{\mathbf{Z}}=\left(Y^{[L]},{\mathbf{X}}^{[J]}\right)=\left({\sum }_{h=1}^L{\eta }_h{\psi }_h,{\sum }_{j=1}^J{\gamma }_j{\mathbf{w}}_j\right)$. Then,

$$\left|{\lambda }_m-{\tilde{\lambda }}_m\right|\to 0\text{and}\parallel \mathbf{Z}-\tilde{\mathbf{Z}}{\parallel }_{\mathcal{H}}\stackrel{p}{\to }0\text{as}L\to \infty \text{and}J\to p.$$

for each $m\in \mathbb{N}$. Let ${\tilde{\xi }}_m$ denote the eigenfunctions corresponding to ${\tilde{\lambda }}_m$, and let ${\tilde{\rho }}_m=\langle \tilde{\mathbf{Z}},{\tilde{\xi }}_m{\rangle }_{\mathcal{H}}$. If both λ_m and ${\tilde{\lambda }}_m$ have multiplicity 1, and $\langle {\xi }_m,{\tilde{\xi }}_m{\rangle }_{\mathcal{H}}\ge 0$, then, for all $m\in \mathbb{N}$.

$$\Vert {\xi }_m-{\tilde{\xi }}_m{\Vert }_{\mathcal{H}}\to 0\text{and}\left|{\rho }_m-{\tilde{\rho }}_m\right|\stackrel{p}{\to }0\text{as}L\to \infty \text{and}J\to p.$$

We now present the theorem that establishes the asymptotic properties of the estimation error. We need the following conditions.

• R1. ${\text{Δ}}_L^y={\sup }_{h=1,\dots ,L}{\left({\tau }_h-{\tau }_{h+1}\right)}^{-1}<\infty$
• R2. ${\text{Δ}}_J^x={\sup }_{j=1,\dots ,J}{}_{,\dots ,J}{\left({\kappa }_j-{\kappa }_{j+1}\right)}^{-1}<\infty$
• R3. $\Vert C_y-{\widehat{C}}_y{\Vert }_{op}=O_p\left(c_n^y\right),\text{where}{c}_n^y\to 0\text{as}n\to \infty$
• R4. $\Vert C_x-{\widehat{C}}_x{\Vert }_{op}=O_p\left(c_n^x\right),\text{where}{c}_n^x\to 0\text{as}n\to \infty ;$
• R5. ${\sum }_{r=1}^p{{\sum }_{k=1}^K\int }_{{\mathcal{T}}_{{}_k}}\text{E}\left\{Y^{(k)}{\left(t_k\right)}^2{X}_r^2\right\}d{t}_k<\infty$
• R6.${\langle {\varphi }_h,{\widehat{\varphi }}_h\rangle }_2\ge 0$ for all h = 1, … L;
• R7.$\langle {\mathbf{w}}_j,{\widehat{\mathbf{w}}}_j\rangle \ge 0$ for all j = 1, … J;
• R8.${\widehat{\eta }}_{ih}={\langle Y_i,{\widehat{\varphi }}_h\rangle }_2$ for all h = 1, …, L and i = 1, …, n.
• R8.${\widehat{\gamma }}_{ij}=\langle {\mathbf{X}}_i,{\widehat{\mathbf{w}}}_j\rangle$ for all j = 1, …, J and i = 1, …, n.

R1 and R2 are standard assumptions for FPCA/MFPCA and PCA, respectively, that guarantee that the first L eigenvalues of C_y and the first J eigenvalues C_x have multiplicity 1.^10,27,36 If these conditions do not hold, the FPCA/MFPCA and PCA are not unique; that is, any unit function or vector in the span of eigenfunctions or eigenvectors of multiplicity greater than 1 can be the direction of FPCA/MFPCA or PCA, respectively. Note that ${\text{Δ}}_L^y$ increases as L increases, and we can set ${\text{Δ}}_J^x\le C$ uniformly over all J for a finite constant C, as it can be assumed that all p eigenvalues of C_x are different in most applications of PCA.²⁷ R3 and R4 state that the estimated covariance operators of functional and vector data converge to respective true values in operator norm ‖·‖_op with rates $c_n^y$ and $c_n^x$ as n → ∞. For instance, $c_n^y=n^{-1/2}$ is established for dense functional data,³⁷ while $c_n^y=n^{-1/2}{h}^{-2}$, with h denoting a certain bandwidth, is obtained for sparse and irregular (SIR) functional data.⁹ For multivariate functional data, we show below (Theorem 7) that $c_n^y=n^{-1/2}$ can be achieved. Lastly, $c_n^x=n^{-1/2}$ is established for vector data with sub-gaussian distribution (e.g., proposition 2.1 in Vershynin³⁸). R5 is required to establish the convergence rate of the cross-covariance operator defined in Appendix S1, that is, the rate of $\Vert C_{yx}-{\widehat{C}}_{yx}{\Vert }_{op}$. Extending the approach of Happ and Greven,²⁶ conditions R1 to R5, combined with R8-R9, are used to establish the convergence rate of the maximum eigenvalue of $V-\widehat{V}$, which in turn is used to establish the convergence rates for the estimation errors. R6 and R7 ensure that true and estimated eigenfunctions and eigenvectors are of the same sign.

Theorem 6. Let ${\widehat{\lambda }}_m$, ${\widehat{\xi }}_{m,}$, and ${\widehat{\rho }}_{im}$ denote the estimates of eigenvalues, PCs and scores of HFV-PCA obtained as described in Section 2.5. Let ${\widehat{\mathbf{Z}}}_i=\left({\sum }_{h=1}^L{\widehat{\eta }}_{ih}{\widehat{\varphi }}_h,{\sum }_{j=1}^J{\widehat{\gamma }}_{ij}{\widehat{\mathbf{w}}}_j\right)$. Assume regularity conditions R1 to R9 hold. Then for all m = 1, …, L + J,

$$\left|{\tilde{\lambda }}_m-{\widehat{\lambda }}_m\right|=O_p\left(L\max \left(n^{-1/2},{\text{Δ}}_L^y{c}_n^y,{\text{Δ}}_J^x{c}_n^x\right)\right),$$

$$\Vert {\tilde{\xi }}_m-\widehat{\xi }{\Vert }_{\mathcal{H}}=O_p\left(L^{3/2}\max \left(n^{-1/2},{\text{Δ}}_L^y{c}_n^y,{\text{Δ}}_J^x{c}_n^x\right)\right),$$

$$\left|{\tilde{\rho }}_{im}-{\widehat{\rho }}_{im}\right|=O_p\left(L^{3/2}\max \left(n^{-1/2},{\text{Δ}}_L^y{c}_n^y,{\text{Δ}}_J^x{c}_n^x\right)\right),$$

$$\Vert {\tilde{\mathbf{Z}}}_i-{\tilde{\mathbf{Z}}}_i{\Vert }_{\mathcal{H}}=O_p\left(\max \left(L{\text{Δ}}_L^y{c}_n^y,{\text{Δ}}_J^x{c}_n^x\right)\right).$$

Combining the results from Theorems 5 and 6 suggests a trade-off between the approximation and estimation errors; that is, for a fixed n, increasing L reduces the approximation error while simultaneously increasing the estimation error. On the other hand, increasing J does not affect the estimation error in an asymptotic sense, as it is bounded above by p, which is fixed. The consistency of the estimators of HFV-PCA components $\left({\widehat{\lambda }}_m,{\widehat{\xi }}_m,{\widehat{\rho }}_{im}\right)$ can be established by assuming, for example, $c_n^y=c_n^x=n^{-1/2}$, ${\tau }_h-{\tau }_{h+1}\ge C^{-1}{h}^{\alpha -1}$ with α > 1, C > 0 (see Hall and Horowitz³⁷), κ_j – κ_j+1 ≥ r with r > 0, and L = O(n^β), where 0 < β < (2α + 5)⁻¹. That is, consistency of $f\left({\widehat{\lambda }}_m,{\widehat{\xi }}_m,{\widehat{\rho }}_{im}\right)$ requires the truncation lag L to grow slower than the sample size n.

We end this section with a theorem that shows that the sample covariance operator of multivariate functional data converges to the population counterpart in operation norm with a desired rate of $c_n^y=n^{-1/2}$.

Theorem 7. Let $C_y:\mathcal{F}\to \mathcal{F}$ and ${\widehat{C}}_y:\mathcal{F}\to \mathcal{F}$, respectively, denote the population and sample covariance operators. For $f\in \mathcal{F}$, kth element of C_yf and ${\widehat{C}}_{y}f$ are, respectively,

$${\left(C_{y}f\right)}^{(k)}=\sum _{k=1}^K{\int }_{{\mathcal{T}}_{{}_k}}{\sigma }_y^{(uk)}\left(s_u,t_k\right)f^{(k)}\left(t_k\right)d{t}_k\text{and}{\left({\widehat{C}}_{y}f\right)}^{(k)}=\sum _{k=1}^K{\int }_{{\mathcal{T}}_{{}_k}}{\widehat{\sigma }}_y^{(uk)}\left(s_u,t_k\right)f^{(k)}\left(t_k\right)d{t}_k,$$

where ${\sigma }_y^{(uk)}\left(s_u,t_k\right)=\mathrm{Cov}\left\{Y^{(u)}\left(s_u\right),Y^{(k)}\left(t_k\right)\right\}$ and ${\widehat{\sigma }}_y^{(uk)}\left(s_u,t_k\right)=n^{-1}{\sum }_{i=1}^n{Y}_i^{(u)}\left(s_u\right)Y_i^{(k)}\left(t_k\right)$. Then, assuming ${\sum }_{k=1}^K{\sum }_{u=1}^K{\int }_{{\mathcal{T}}_{{}_k}}{\int }_{{\mathcal{T}}_{{}_u}}E\left\{Y_i^{(u)}{\left(s_u\right)}^2{Y}_i^{(k)}{\left(t_k\right)}^2\right\}d{s}_{u}d{t}_k<\infty$, we have:

$$\Vert C_y-{\widehat{C}}_y{\Vert }_{op}=Op(n^{-1/2}).$$

3 |. SIMULATIONS

In this section, we conduct simulation studies to examine the finite-sample performance of the proposed HFV-PCA.

3.1 |. Univariate functional data and vector data

We first consider hybrid observations consisting of univariate functional data (K = 1) and 10-dimensional vector data (p = 10), Z_i = (Y_i, X_i), i = 1, …, n, that are generated according to the following truncated hybrid PC decomposition with 10 components:

$${\mathbf{Z}}_i[t]=\sum _{m=1}^{10}{\rho }_{im}{\xi }_m[t]+{ϵ}_i[t],t\in \mathcal{T}=[0,1],$$ (11)

where ${ϵ}_i[t]={\left[{ϵ}_i(t),\mathbf{0}\right]}^T$ are measurement errors on the functional part with ϵ_i(t) i.i.d. as $\mathcal{N}(0,0.4)$. Such measurement errors are natural and commonly assumed in functional data analysis, where actual observations are discrete and deviate from the underlying smooth curve.^25,28 We consider two settings that differ in the formulation of the functional part of the hybrid PCs, ξ_m = (ψ_m, θ_m). In setting I, we set ψ_2j−1 (t) = sin(2jπt) and ψ_2j(t) = cos(2jπt) for j = 1, …, 5. In setting II, we set {ψ_m(t), m = 1, …, 10} as the first 10 normalized legendre polynomials divided by $\sqrt{2}$. In both settings, we set the vector part of hybrid PCs {θ₁, …, θ₁₀} as the first 10 eigenvectors of a 10 × 10 compound symmetry correlation matrix with off-diagonal elements equal to 0.2; the exact values of these eigenvectors are presented in Appendix S2. The hybrid PC scores are independently generated from $\mathcal{N}\left(0,{\lambda }_m\right)$, where λ_m = 0.5^m−1, m = 1, …, 10. Here, we consider sample sizes of n = 100 and n = 200.

To assess the sensitivity of the proposed HFV-PCA to varying distribution and density of observed functions, we consider the following three types of functional data: (1) SIR functional data, where each function is sampled at a random number of points chosen from a discrete uniform distribution on {5, …, 10}, and the locations of the measurements were randomly drawn from a uniformly distributed grid {(t – 1)/59; t = 1, …, 60} ; 2) dense and irregular (DIR) functional data, where the number of points for each function is randomly chosen from {10, …, 40}, and the locations are randomly drawn from {(t – 1)/59; t = 1, …, 60}; and 3) dense and regular (DR) functional data, where all functions are observed on {(t – 1)/59; t = 1, …, 60}.

Under each scenario (12 scenarios: n = 100/200, setting I/II and SIR/DIR/DR), the accuracy of the three leading eigenvalues and hybrid PCs estimated by the procedure described in Section 2.5 is quantified by the relative squared error (RSE): $\mathrm{RSE}\left({\widehat{\lambda }}_m\right)={\left({\lambda }_m-{\widehat{\lambda }}_m\right)}^2/{\lambda }_m^2$ and $\mathrm{RSE}\left({\widehat{\xi }}_m\right)=\Vert {\xi }_m-{\widehat{\xi }}_m{\Vert }_{\mathcal{H}}^2$, m = 1, 2, 3. Note that since the hybrid PCs are only unique up to their respective signs, we use $s_m=\mathrm{sign}\left(\langle {\xi }_m,{\widehat{\xi }}_m{\rangle }_{\mathcal{H}}\right)$ to set ${\widehat{\xi }}_m=s_m{\widehat{\xi }}_m$ so that the signs are consistent. Another outcome measure is the average squared error (ASE) of the corresponding hybrid PC scores: $\mathrm{ASE}\left({\widehat{\rho }}_m\right)=n^{-1}{\sum }_{i=1}^n{\left({\widehat{\rho }}_{im}-{\rho }_{im}\right)}^2$.

The proposed HFV-PCA was applied to each simulated dataset using the estimation scheme described in Section 2.5. Specifically, we first performed FPCA⁹ on the functional part of the generated hybrid data to estimate and retain the first L functional PCs that jointly explain 99% of the functional data variability. Likewise, we applied the classical PCA²⁷ to the vector part to obtain the first J vector PCs that cumulatively capture 99% of the variance in vector data. We then combined the estimated FPCA and PCA components in a way that produces consistent estimates of the HFV-PCA components—see steps (c) to (e) in Section 2.5. We also compared the performance of the proposed HFV-PCA to the competing method by Ramsay and Silverman,²⁸ which is briefly described in Section 1. In our simulation study, 11 Fourier basis functions were used to presmooth the functional parts and produce Fourier coefficients, which were augmented by the corresponding vector part. Note that such applications of Ramsay and Silverman’s method under settings I and II, respectively, correspond to correctly specified and misspecified basis functions for pre-smoothing.

Table 1 reports RSEs and ASEs averaged across 500 simulated datasets of size n = 100 under each setting (I/II) and functional data type (SIR/DIR/DR). For DR functional data, HFV-PCA and Ramsay and Silverman’s method show comparable performance, at least when the basis functions are correctly specified for the latter method (Setting I). When the basis functions are misspecified (Setting II), RSE ratios of HFV-PCA to Ramsay and Silverman’s method are as low as 0.3 to 0.4 for some components, and the ASE ratios are around 0.72 to 0.94. The discrepancy in the performance between the two methods increases for DIR functional data, where HFV-PCA outperforms Ramsay and Silverman’s method with respect to most components. Specifically, the RSE and ASE ratios are between 0.7 and 0.9 (except for the second and third hybrid PCs) under Setting I, and between 0.35 and 0.95 (except for the first eigenvalue and second hybrid PC) under Setting II. For SIR functional data, we find that the gains in the estimation and prediction accuracy are dramatic when switching from Ramsay and Silverman’s method to our HFV-PCA. Under Setting I, the RSE and ASE ratios are between 0.06 and 0.22, indicating that RSEs and ASEs are reduced by 78% to 94% using HFV-PCA as compared to using Ramsay and Silverman’s method. The gains are more substantial under Setting 2, where the ratios are smaller than 0.15 for all components. The severe underperformance of Ramsay and Silverman’s method on SIR functional data is mainly attributed to its presmoothing step that approximates each function as a linear combination of Fourier basis functions and coefficients. Specifically, many of the basis coefficients estimated from a SIR function will have very high or even infinite variance, making it impossible to accurately represent each function using any reasonable basis.³⁹ This, in turn, severely negatively affects the ability of Ramsay and Silverman’s method to precisely estimate hybrid PCs and scores. On the other hand, the proposed method maintains satisfactory performance in all configurations, as its estimation scheme allows to flexibly incorporate the most appropriate FPCA method given particular type/sparsity of functional data.

TABLE 1.

Performance of principal component analysis (PCA) of hybrid functional and vector data (HFV-PCA) and Ramsay and Silverman’s method (RS-PCA) in terms of $\mathrm{RSE}\left({\widehat{\lambda }}_m\right)$, $\mathrm{RSE}\left({\widehat{\xi }}_m\right)$ and $\mathrm{ASE}\left({\widehat{\rho }}_m\right)$, m = 1,2,3, averaged across 500 simulated datasets of size n = 100 (with SDs in parentheses) for each setting (I/II) and functional data type (SIR/DIR/DR). “Ratio” denotes the RSE and ASE ratios of HFV-PCA to RS-PCA

		Setting I			Setting II
Type	R(A)SE	HFV-PCA	RS-PCA	Ratio	HFV-PCA	RS-PCA	Ratio
SIR	$\mathrm{RSE}\left({\widehat{\lambda }}_1\right)$	0.038 (0.040)	0.245 (0.780)	0.154	0.031 (0.035)	2.017 (8.693)	0.016
	$\mathrm{RSE}\left({\widehat{\lambda }}_2\right)$	0.062 (0.057)	0.576 (0.609)	0.107	0.063 (0.060)	1.270 (1.960)	0.050
	$\mathrm{RSE}\left({\widehat{\lambda }}_3\right)$	0.197 (0.082)	1.166 (1.084)	0.169	0.152 (0.086)	3.191 (2.297)	0.048
	$\mathrm{RSE}\left({\widehat{\xi }}_1\right)$	0.047 (0.041)	0.236 (0.316)	0.198	0.046 (0.045)	0.683 (0.432)	0.067
	$\mathrm{RSE}\left({\widehat{\xi }}_2\right)$	0.081 (0.053)	0.449 (0.392)	0.180	0.101 (0.073)	0.844 (0.519)	0.120
	$\mathrm{RSE}\left({\widehat{\xi }}_3\right)$	0.308 (0.109)	1.396 (0.515)	0.221	0.248 (0.153)	1.696 (0.258)	0.146
	$\mathrm{ASE}\left({\widehat{\rho }}_1\right)$	0.060 (0.026)	0.531 (0.505)	0.113	0.074 (0.028)	1.368 (1.282)	0.054
	$\mathrm{ASE}\left({\widehat{\rho }}_2\right)$	0.059 (0.032)	0.550 (0.327)	0.107	0.071 (0.036)	0.888 (0.439)	0.080
	$\mathrm{ASE}\left({\widehat{\rho }}_3\right)$	0.034 (0.013)	0.579 (0.209)	0.058	0.041 (0.020)	0.805 (0.197)	0.051
DIR	$\mathrm{RSE}\left({\widehat{\lambda }}_1\right)$	0.020 (0.030)	0.023 (0.036)	0.889	0.024 (0.027)	0.021 (0.031)	1.138
	$\mathrm{RSE}\left({\widehat{\lambda }}_2\right)$	0.018 (0.023)	0.020 (0.030)	0.888	0.021 (0.026)	0.023 (0.033)	0.927
	$\mathrm{RSE}\left({\widehat{\lambda }}_3\right)$	0.018 (0.022)	0.023 (0.030)	0.779	0.022 (0.036)	0.030 (0.046)	0.735
	$\mathrm{RSE}\left({\widehat{\xi }}_1\right)$	0.028 (0.027)	0.034 (0.036)	0.826	0.055 (0.041)	0.120 (0.069)	0.459
	$\mathrm{RSE}\left({\widehat{\xi }}_2\right)$	0.072 (0.051)	0.061 (0.054)	1.186	0.084 (0.063)	0.073 (0.074)	1.144
	$\mathrm{RSE}\left({\widehat{\xi }}_3\right)$	0.094 (0.061)	0.080 (0.072)	1.169	0.121 (0.114)	0.344 (0.252)	0.353
	$\mathrm{ASE}\left({\widehat{\rho }}_1\right)$	0.034 (0.019)	0.043 (0.026)	0.798	0.046 (0.026)	0.070 (0.054)	0.665
	$\mathrm{ASE}\left({\widehat{\rho }}_2\right)$	0.046 (0.028)	0.053 (0.035)	0.874	0.057 (0.037)	0.076 (0.051)	0.750
	$\mathrm{ASE}\left({\widehat{\rho }}_3\right)$	0.037 (0.019)	0.041 (0.021)	0.912	0.049 (0.031)	0.065 (0.067)	0.754
DR	$\mathrm{RSE}\left({\widehat{\lambda }}_1\right)$	0.021 (0.033)	0.021 (0.033)	0.999	0.022 (0.033)	0.021 (0.026)	1.042
	$\mathrm{RSE}\left({\widehat{\lambda }}_2\right)$	0.017 (0.024)	0.017 (0.024)	1.006	0.018 (0.024)	0.017 (0.024)	1.007
	$\mathrm{RSE}\left({\widehat{\lambda }}_3\right)$	0.019 (0.025)	0.019 (0.025)	0.998	0.019 (0.025)	0.036 (0.038)	0.532
	$\mathrm{RSE}\left({\widehat{\xi }}_1\right)$	0.030 (0.032)	0.032 (0.035)	0.943	0.036 (0.033)	0.100 (0.050)	0.361
	$\mathrm{RSE}\left({\widehat{\xi }}_2\right)$	0.057 (0.051)	0.055 (0.051)	1.042	0.062 (0.054)	0.055 (0.056)	1.126
	$\mathrm{RSE}\left({\widehat{\xi }}_3\right)$	0.061 (0.056)	0.062 (0.058)	0.979	0.075 (0.086)	0.234 (0.133)	0.319
	$\mathrm{ASE}\left({\widehat{\rho }}_1\right)$	0.025 (0.022)	0.026 (0.023)	0.963	0.026 (0.022)	0.037 (0.032)	0.720
	$\mathrm{ASE}\left({\widehat{\rho }}_2\right)$	0.036 (0.032)	0.055 (0.033)	0.987	0.037 (0.032)	0.040 (0.041)	0.935
	$\mathrm{ASE}\left({\widehat{\rho }}_3\right)$	0.024 (0.019)	0.062 (0.019)	0.997	0.025 (0.021)	0.030 (0.025)	0.818

Abbreviations: ASE, average squared error; DR, dense and regular; DIR, dense and irregular; RSE, relative squared error; SIR, sparse and irregular.

Table 2 presents the same statistics for n = 200. The RSEs and ASEs decrease in all configurations, suggesting the consistency of our estimation scheme. The degree of gains in estimation and predictive accuracy by using HFV-PCA over Ramsay and Silverman’s method is similar to the case when n = 100. In sum, the simulation results show that the proposed HFV-PCA performs well under varying sparsity and patterns of functional data and is much more robust compared to the existing method.

TABLE 2.

Performance of principal component analysis (PCA) of hybrid functional and vector data (HFV-PCA) and Ramsay and Silverman’s method (RS-PCA) in terms of $\mathrm{RSE}\left({\widehat{\lambda }}_m\right)$, $\mathrm{RSE}\left({\widehat{\xi }}_m\right)$ and $\mathrm{ASE}\left({\widehat{\rho }}_m\right)$, m = 1,2,3, averaged across 500 simulated datasets of size n = 200 (with standard deviations in parentheses) for each setting (I/II) and functional data type (SIR/DIR/DR). “Ratio” denotes the RSE and ASE ratios of HFV-PCA to RS-PCA

		Setting I			Setting II
Type	R(A)SE	HFV-PCA	RS-PCA	Ratio	HFV-PCA	RS-PCA	Ratio
SIR	$\mathrm{RSE}\left({\widehat{\lambda }}_1\right)$	0.025 (0.026)	0.134 (0.245)	0.189	0.019 (0.022)	1.207 (6.743)	0.016
	$\mathrm{RSE}\left({\widehat{\lambda }}_2\right)$	0.050 (0.041)	0.493 (0.527)	0.102	0.048 (0.045)	1.168 (1.183)	0.041
	$\mathrm{RSE}\left({\widehat{\lambda }}_3\right)$	0.192 (0.057)	1.152 (0.939)	0.167	0.138 (0.066)	3.642 (1.964)	0.038
	$\mathrm{RSE}\left({\widehat{\xi }}_1\right)$	0.024 (0.020)	0.148 (0.213)	0.161	0.021 (0.018)	0.584 (0.381)	0.036
	$\mathrm{RSE}\left({\widehat{\xi }}_2\right)$	0.045 (0.027)	0.339 (0.307)	0.132	0.052 (0.036)	0.761 (0.501)	0.068
	$\mathrm{RSE}\left({\widehat{\xi }}_3\right)$	0.255 (0.068)	1.579 (0.418)	0.162	0.165 (0.094)	1.783 (0.181)	0.092
	$\mathrm{ASE}\left({\widehat{\rho }}_1\right)$	0.047 (0.012)	0.427 (0.333)	0.111	0.059 (0.012)	1.193 (1.008)	0.049
	$\mathrm{ASE}\left({\widehat{\rho }}_2\right)$	0.043 (0.015)	0.484 (0.278)	0.088	0.052 (0.016)	0.856 (0.415)	0.060
	$\mathrm{ASE}\left({\widehat{\rho }}_3\right)$	0.026 (0.007)	0.634 (0.172)	0.041	0.030 (0.010)	0.886 (0.148)	0.034
DIR	$\mathrm{RSE}\left({\widehat{\lambda }}_1\right)$	0.010 (0.013)	0.011 (0.016)	0.903	0.015 (0.011)	0.011 (0.014)	1.336
	$\mathrm{RSE}\left({\widehat{\lambda }}_2\right)$	0.012 (0.015)	0.013 (0.018)	0.931	0.016 (0.017)	0.017 (0.023)	0.946
	$\mathrm{RSE}\left({\widehat{\lambda }}_3\right)$	0.009 (0.014)	0.013 (0.022)	0.700	0.011 (0.021)	0.021 (0.028)	0.499
	$\mathrm{RSE}\left({\widehat{\xi }}_1\right)$	0.015 (0.013)	0.017 (0.016)	0.889	0.091 (0.027)	0.091 (0.027)	0.396
	$\mathrm{RSE}\left({\widehat{\xi }}_2\right)$	0.047 (0.028)	0.031 (0.025)	1.514	0.037 (0.041)	0.037 (0.041)	1.292
	$\mathrm{RSE}\left({\widehat{\xi }}_3\right)$	0.060 (0.030)	0.040 (0.027)	1.500	0.265 (0.151)	0.265 (0.151)	0.265
	$\mathrm{ASE}\left({\widehat{\rho }}_1\right)$	0.024 (0.009)	0.030 (0.012)	0.796	0.033 (0.011)	0.051 (0.033)	0.655
	$\mathrm{ASE}\left({\widehat{\rho }}_2\right)$	0.032 (0.014)	0.035 (0.017)	0.918	0.037 (0.015)	0.053 (0.026)	0.703
	$\mathrm{ASE}\left({\widehat{\rho }}_3\right)$	0.028 (0.011)	0.029 (0.010)	0.938	0.036 (0.014)	0.047 (0.047)	0.772
DR	$\mathrm{RSE}\left({\widehat{\lambda }}_1\right)$	0.010 (0.014)	0.010 (0.014)	0.999	0.010 (0.015)	0.012 (0.014)	0.867
	$\mathrm{RSE}\left({\widehat{\lambda }}_2\right)$	0.010 (0.014)	0.010 (0.014)	1.012	0.011 (0.014)	0.010 (0.014)	1.015
	$\mathrm{RSE}\left({\widehat{\lambda }}_3\right)$	0.010 (0.015)	0.010 (0.015)	1.004	0.010 (0.014)	0.028 (0.024)	0.352
	$\mathrm{RSE}\left({\widehat{\xi }}_1\right)$	0.014 (0.014)	0.015 (0.015)	0.950	0.020 (0.014)	0.078 (0.018)	0.251
	$\mathrm{RSE}\left({\widehat{\xi }}_2\right)$	0.029 (0.025)	0.027 (0.024)	1.098	0.034 (0.023)	0.025 (0.021)	1.343
	$\mathrm{RSE}\left({\widehat{\xi }}_3\right)$	0.030 (0.025)	0.031 (0.026)	0.983	0.041 (0.025)	0.192 (0.033)	0.212
	$\mathrm{ASE}\left({\widehat{\rho }}_1\right)$	0.013 (0.009)	0.014 (0.010)	0.972	0.014 (0.009)	0.021 (0.012)	0.664
	$\mathrm{ASE}\left({\widehat{\rho }}_2\right)$	0.019 (0.015)	0.019 (0.015)	0.999	0.019 (0.014)	0.019 (0.016)	0.995
	$\mathrm{ASE}\left({\widehat{\rho }}_3\right)$	0.014 (0.010)	0.014 (0.010)	0.999	0.014 (0.009)	0.019 (0.008)	0.747

Abbreviations: ASE, average squared error; DR, dense and regular; DIR, dense and irregular; RSE, relative squared error; SIR, sparse and irregular.

3.2 |. Multivariate functional data and vector data

We will now consider hybrid obsevations consisting of multivariate functional data (K = 2) and 10-dimensional vector data (p = 10), ${\mathbf{Z}}_i=\left(Y_i^{(1)},Y_i^{(2)},{\mathbf{X}}_i\right)$, i = 1, …, n, that are generated according to the truncated hybrid PC decomposition with 10 components as in (11). Herein, the functional part of each hybrid PC ${\xi }_m=\left({\psi }_m^{(1)},{\psi }_m^{(2)},{\theta }_m\right)$, m = 1, …, 10, consists of two functions, ${\psi }_m^{(1)}$ and ${\psi }_m^{(2)}$, defined on a unit interval [0, 1]. In Setting I, they both take the form of ${\psi }_{2j-1}^{(k)}\left(t_k\right)=2^{-1/2}\sin \left(2j\pi t_k\right)$, ${\psi }_{2j}^{(k)}\left(t_k\right)=2^{-1/2}\cos \left(2j\pi t_k\right)$, k = 1, 2, j = 1, …, 5. In setting II, we keep the same form for ${\psi }_m^{(1)}$ but set ${\psi }_m^{(2)}$ as the first 10 normalized Legendre polynomials divided by 2; that is, the basis systems of ${\psi }_m^{(1)}$ and ${\psi }_m^{(2)}$ differ. Measurement error term is set as ${ϵ}_i[\mathbf{t}]={\left[{ϵ}_i^{(1)}\left(t_1\right),{ϵ}_i^{(2)}\left(t_2\right),\mathbf{0}\right]}^T$, where ${ϵ}_i^{(1)}\left(t_1\right)$ and ${ϵ}_i^{(2)}\left(t_2\right)$ are i.i.d. $\mathcal{N}(0,0.4)$. The vector part of each hybrid PC, θ_m, is set as in Section 3.1. The hybrid PC scores, p_im, are independently generated from $\mathcal{N}\left(0,{\lambda }_m\right)$ with λ_m = 0.5^m−1. We consider sample sizes of n = 150 and n = 300.

The following three combinations of the types of functional data are considered: (a) Y⁽¹⁾ and Y⁽²⁾ are both SIR (SIR-SIR); (b) Y⁽¹⁾ and Y⁽²⁾ are SIR and DR, respectively (SIR-DR); and c) Y⁽¹⁾ and Y⁽²⁾ are both DR (DR-DR). The proposed HFV-PCA was applied to each simulated dataset as done in Section 3.1, except that here, MFPCA²⁶ was applied to Y⁽¹⁾ and Y⁽²⁾ to extract multivariate functional PCs. For performance evaluation, $\mathrm{RSE}\left({\widehat{\lambda }}_m\right)$, $\mathrm{RSE}\left({\widehat{\xi }}_m\right)$, and $\mathrm{ASE}\left({\widehat{\rho }}_m\right)$, m = 1, 2, 3, are averaged across 500 datasets, as in Section 3.1.

Table 3 presents the RSEs of the three leading eigenvalues and hybrid PCs and the ASEs of the three leading hybrid PC scores given multivariate functional and vector data. The performance of HFV-PCA is similar to the simple case of univariate and vector functional data considered in Section 3.1. As expected, the RSEs and ASEs decrease as the sample size and the density of observed functional data increase. Specifically, the proposed method shows excellent performance when both or one of functions are DR, with small RSEs and ASEs for most HFV-PCA components. But even when both functions are SIR, the proposed method is able to yield acceptable results with small to moderate RSEs and ASEs (all less than or around 0.2). We see that the results are very similar between the two settings, suggesting that the proposed non-parametric estimation scheme is robust to varying distributions of multivariate functional data.

TABLE 3.

Performance of principal component analysis (PCA) of hybrid functional and vector data (HFV-PCA) in terms of $\mathrm{RSE}\left({\widehat{\lambda }}_m\right)$, $\mathrm{RSE}\left({\widehat{\xi }}_m\right)$ and $\mathrm{ASE}\left({\widehat{\rho }}_m\right)$, m = 1, 2, 3, averaged across 500 simulated datasets of sizes n = 150 and n = 300 (with SDs in parentheses) for each setting (I/II). Given two functions per observation unit, three combinations of the types of multivariate functional data are considered: SIR-SIR, SIR-DR, and DR-DR

		Setting I			Setting II
n	R(A)SE	SIR-SIR	SIR-DR	DR-DR	SIR-SIR	SIR-DR	DR-DR
150	$\mathrm{RSE}\left({\widehat{\lambda }}_1\right)$	0.054 (0.044)	0.026 (0.027)	0.014 (0.019)	0.054 (0.045)	0.025 (0.027)	0.014 (0.019)
	$\mathrm{RSE}\left({\widehat{\lambda }}_2\right)$	0.104 (0.060)	0.042 (0.038)	0.014 (0.018)	0.104 (0.061)	0.042 (0.037)	0.014 (0.018)
	$\mathrm{RSE}\left({\widehat{\lambda }}_3\right)$	0.183 (0.067)	0.075 (0.049)	0.021 (0.026)	0.174 (0.068)	0.072 (0.049)	0.020 (0.024)
	$\mathrm{RSE}\left({\widehat{\xi }}_1\right)$	0.047 (0.026)	0.035 (0.023)	0.020 (0.022)	0.049 (0.027)	0.035 (0.023)	0.020 (0.022)
	$\mathrm{RSE}\left({\widehat{\xi }}_2\right)$	0.108 (0.043)	0.076 (0.037)	0.037 (0.032)	0.115 (0.048)	0.076 (0.038)	0.037 (0.033)
	$\mathrm{RSE}\left({\widehat{\xi }}_3\right)$	0.277 (0.077)	0.161 (0.056)	0.045 (0.036)	0.273 (0.083)	0.161 (0.055)	0.045 (0.036)
	$\mathrm{ASE}\left({\widehat{\rho }}_1\right)$	0.044 (0.013)	0.026 (0.012)	0.017 (0.012)	0.046 (0.013)	0.026 (0.012)	0.017 (0.012)
	$\mathrm{ASE}\left({\widehat{\rho }}_2\right)$	0.043 (0.019)	0.029 (0.019)	0.024 (0.021)	0.045 (0.020)	0.029 (0.019)	0.024 (0.021)
	$\mathrm{ASE}\left({\widehat{\rho }}_3\right)$	0.030 (0.011)	0.020 (0.012)	0.017 (0.012)	0.031 (0.012)	0.020 (0.012)	0.017 (0.012)
300	$\mathrm{RSE}\left({\widehat{\lambda }}_1\right)$	0.046 (0.031)	0.018 (0.018)	0.007 (0.009)	0.047 (0.031)	0.018 (0.018)	0.007 (0.009)
	$\mathrm{RSE}\left({\widehat{\lambda }}_2\right)$	0.093 (0.043)	0.035 (0.026)	0.008 (0.011)	0.095 (0.043)	0.034 (0.026)	0.008 (0.011)
	$\mathrm{RSE}\left({\widehat{\lambda }}_3\right)$	0.180 (0.047)	0.070 (0.034)	0.015 (0.017)	0.173 (0.048)	0.068 (0.033)	0.014 (0.016)
	$\mathrm{RSE}\left({\widehat{\xi }}_1\right)$	0.031 (0.013)	0.023 (0.013)	0.011 (0.012)	0.031 (0.014)	0.023 (0.013)	0.011 (0.012)
	$\mathrm{RSE}\left({\widehat{\xi }}_2\right)$	0.074 (0.025)	0.052 (0.022)	0.019 (0.016)	0.078 (0.026)	0.052 (0.022)	0.019 (0.016)
	$\mathrm{RSE}\left({\widehat{\xi }}_3\right)$	0.215 (0.054)	0.121 (0.037)	0.022 (0.016)	0.212 (0.057)	0.121 (0.037)	0.022 (0.016)
	$\mathrm{ASE}\left({\widehat{\rho }}_1\right)$	0.037 (0.007)	0.020 (0.007)	0.010 (0.007)	0.039 (0.007)	0.020 (0.007)	0.011 (0.007)
	$\mathrm{ASE}\left({\widehat{\rho }}_2\right)$	0.034 (0.011)	0.020 (0.011)	0.014 (0.011)	0.035 (0.011)	0.020 (0.011)	0.014 (0.011)
	$\mathrm{ASE}\left({\widehat{\rho }}_3\right)$	0.023 (0.005)	0.013 (0.006)	0.010 (0.006)	0.023 (0.006)	0.013 (0.006)	0.009 (0.006)

Abbreviations: ASE, average squared error; DR, dense and regular; DIR, dense and irregular; RSE, relative squared error; SIR, sparse and irregular.

4 |. APPLICATION TO RENAL STUDY

In this section, we apply the proposed HFV-PCA to renal study data collected at Emory University during the period of January 1998 to July 2008 (a.k.a. the Emory renal study). Renal obstruction is a serious clinical problem that can lead to irreversible loss of renal function if not properly treated. In recent years, diuresis renography has been widely adopted as a cost-effective and noninvasive approach to detect renal obstruction.⁴⁰ The procedure starts with an intravenous injection of a gamma emitting tracer, ^99mTc-Mercaptoacetyltriglycine (MAG3), which is rapidly removed from the blood by the kidneys and then travels down the ureters from the kidney to the bladder. Then, a set of renogram curves is generated by quantifying and recording the MAG3 photon counts inside the kidney over time.⁴¹ The first renogram curve (called baseline) consists of the MAG3 photon counts detected at 59 time points during an initial period of 24 minutes (see the left panel in Figure 1). The second renogram curve (called post-furosemide) is obtained at 40 time points during an additional period of 20 minutes after an intravenous injection of furosemide (see the right panel in Figure 1). There are several interpretable features of renogram curves that suggest high/low likelihood of renal obstruction.⁴² Typically, the renogram curves of an unobstructed kidney is characterized by a quick uptake and immediate excretion of MAG3, suggesting no blockage (see dashed lines in the top panel of Figure 1). On the other hand, the obstructed kidney’s baseline curve exhibits a prolonged period of MAG3 accumulation, followed by its poor excretion to the bladder throughout the post-furosemide renogram (see solid lines in the top panel of Figure 1). However, in practice, there is a high kidney-to-kidney variability in renogram curves, and many of them show patterns that are not clear-cut (see bottom panel of Figure 1). To further facilitate interpretation of diuresis renography, several pharmacokinetic parameters are also generated from the MAG3 scan.⁴¹ These parameters quantify various pharmacokinetic properties of baseline and post-furosemide renogram curves in the whole kidney, pelvis and cortical regions (e.g., time to peak photon counts, photon counts in the last minute of furosemide acquisition divided by the maximum baseline acquisition counts) that are important for evaluating possible renal obstruction. In addition, four clinical variables are also collected for each kidney. The first clinical variable is kidney’s age. The other three clinical variables are scores provided by three nuclear medicine experts which range from −1 to 1, with scores closer to 1 indicating higher likelihood of renal obstruction. In sum, each kidney has 18 renogram variables (4 clinical variables and 14 pharmacokinetic parameters), which are listed in Table 4. In general, larger values of the renogram variables are associated with reduced kidney’s ability to drain (higher likelihood of renal obstruction), though they are highly variable and have no clear cutoff values to separate obstructed from nonobstructed kidneys.

FIGURE 1.

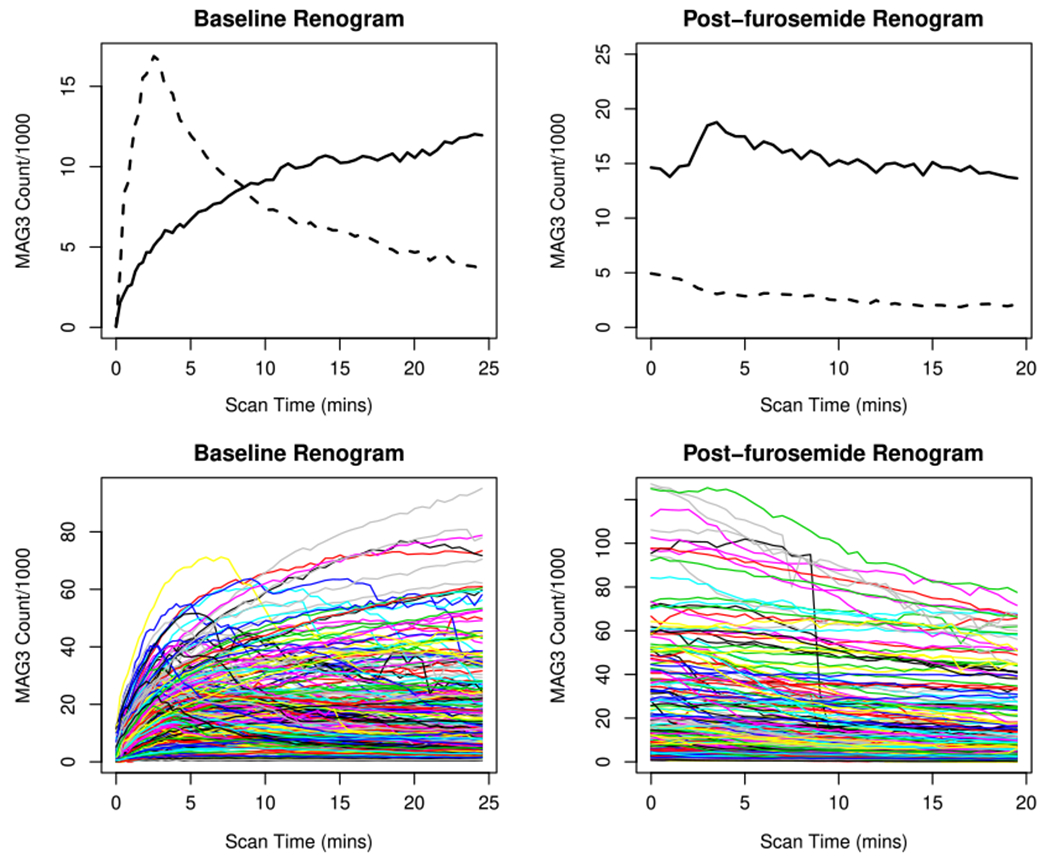
The top panel presents the baseline (left) and post-furosemide (right) renogram curves of 2 kidneys that are diagnosed as “non-obstructed” (dashed lines) and “obstructed” (solid lines). The bottom panel shows baseline and post-furosemide renogram curves of 253 kidneys. [Colour figure can be viewed at wileyonlinelibrary.com]

TABLE 4.

Eighteen renogram variables (4 clinical and 14 pharmacokinetic variables)

Index	Variable	Description
1	Age	Range: 18 to 87 years
2-4	Expert’s Score (from 3 experts)	Ranges from −1.0 to 1.0 with higher scores indicating higher likelihood of obstruction
5	Cortical AUC-d1	Area under the first derivative of cortical renogram
6	BL AUC-d1	Area under the first derivative of BL renogram
7	Cortical mv	Minimum velocity (mv) of the cortical renogram
8	BL mv	Minimum velocity (mv) of BL renogram
9	Cortical tminv	Time to minimum velocity (tminv) of cortical renogram
10	BL tminv	Time to minimum velocity (tminv) BL renogram
11	Cortical tmax	Time to maximum (tmax) of cortical renogram
12	BL tmax	Time to maximum (tmax) of BL renogram
13	PF AUC	Area under the PF renogram
14	Pelvis AUC	Area under the renogram of the pelvis region
15	PF max	Maximum (max) of the PF renogram
16	Pelvis max	Maximum (max) of the pelvis renogram
17	lastPF/maxBL	Ratio of PF renogram at last time point to BL max
18	flrstPF/maxBL	Ratio of PF renogram at first time point to BL max

Abbreviations: BL, Baseline; PF, post-furosemide.

Given such a lack of definite guidance on using renogram curves and variables to detect renal obstruction,⁴² the Emory renal study aims to identify and understand co-varying patterns of renogram curves and variables that provide further insights into underlying physiological mechanisms of renal obstruction. The dataset contains 253 kidneys of 131 subjects (66 men [50.4%], 65 women [49.6%]; mean age, 58 years; SD, 16 years; range, 18-87 years) randomly selected from the Emory University Hospital’s archived database. Each kidney has baseline and post-furosemide renogram curves, each of which is assumed to be realizations of an underlying smooth random process that quantifies MAG3 photon counts as a function of scan time. Following the notation introduced in Section 2, $Y_i^{(1)}$ and $Y_i^{(2)}$, respectively, denote the baseline and post-furosemide renogram curves of ith kidney (i = 1, …, 253). Eighteen renogram variables constitute the vector data for each kidney; that is, ${\mathbf{X}}_i\in {\mathbb{R}}^{18}$.

To address the goal of the study, we applied HFV-PCA to hybrid data ${\mathbf{Z}}_i=\left(Y_i^{(1)},Y_i^{(2)},{\mathbf{X}}_i\right)$ consisting of bivariate (K = 2) functional and 18-dimensional vector data. We first standardized Xi and rescaled it as ${\mathbf{X}}_i^{\ast }={\omega }^{1/2}{\mathbf{X}}_i$, using ω from (10). We then applied MFPCA²⁶ on $Y_i=\left(Y_i^{(1)},Y_i^{(2)}\right)$ and classical PCA on ${\mathbf{X}}_i^{*}$ to estimate and retain the first L = 4 functional PCs and the first J = 13 vector PCs that explain 99% of variability in functional and vector data, respectively. Finally, the estimated MFPCA and PCA components were combined, following steps (c) to (e) in Section 2.5, to produce consistent estimates of the HFV-PCA components.

Figure 2 depicts the first estimated hybrid PC, ${\widehat{\xi }}_1=\left({\widehat{\psi }}_1^{(1)},{\widehat{\psi }}_1^{(2)},{\widehat{\theta }}_1\right)$ which explains 73% of the total variability in the data. Specifically, the top left and right panels respectively show the functional parts of the first estimated hybrid PC, ${\widehat{\psi }}_1^{(1)}$ and ${\widehat{\psi }}_1^{(2)}$ which correspond to the baseline and post-furosemide scans, respectively. The baseline PC ${\widehat{\psi }}_1^{(1)}$ consists of an increasing positive contribution over time; that is, the greatest variability among baseline renogram curves is observed in the later scan period. On the other hand, the post-furosemide PC ${\widehat{\psi }}_1^{(2)}$ is characterized by a positive contribution that decreases over time. To aid in interpretation of the baseline and post-furosemide PCs, the middle panel of Figure 2 (left: baseline; right: post-furosemide) shows the mean function ${\widehat{\mu }}^{(k)}=n^{-1}{\sum }_{i=1}^n{Y}_i^{(k)}$ (solid line) and the functions obtained by adding (+) and subtracting (−) a suitable multiple of ${\psi }_1^{(k)}$, k = 1, 2. We see that the baseline PC clearly distinguishes one pattern that exhibits a prolonged period of accumulation of MAG3 inside a kidney (+) from another that is characterized by a quick uptake of MAG3 followed by its quick drainage to the bladder (−). The post-furosemide corresponds to a variation in the overall MAG3 level that is either elevated (+) or reduced (−) relative to the mean throughout the scan period. Thus, ${\psi }_1^{(1)}$ and ${\psi }_1^{(2)}$ differentiate between kidneys according to their ability to quickly drain MAG3. The last panel of Figure 2 depicts the vector part of the first hybrid PC. All weights are positive, thereby separating kidneys with normal and reduced ability to drain, and being consistent with the direction of variability captured by the functional parts. In sum, the first hybrid PC is interpretable as a renal obstruction-related effect, as co-varying patterns of renogram curves and variables for positive scores agree with the well-known physiological mechanism of renal obstruction.

FIGURE 2.

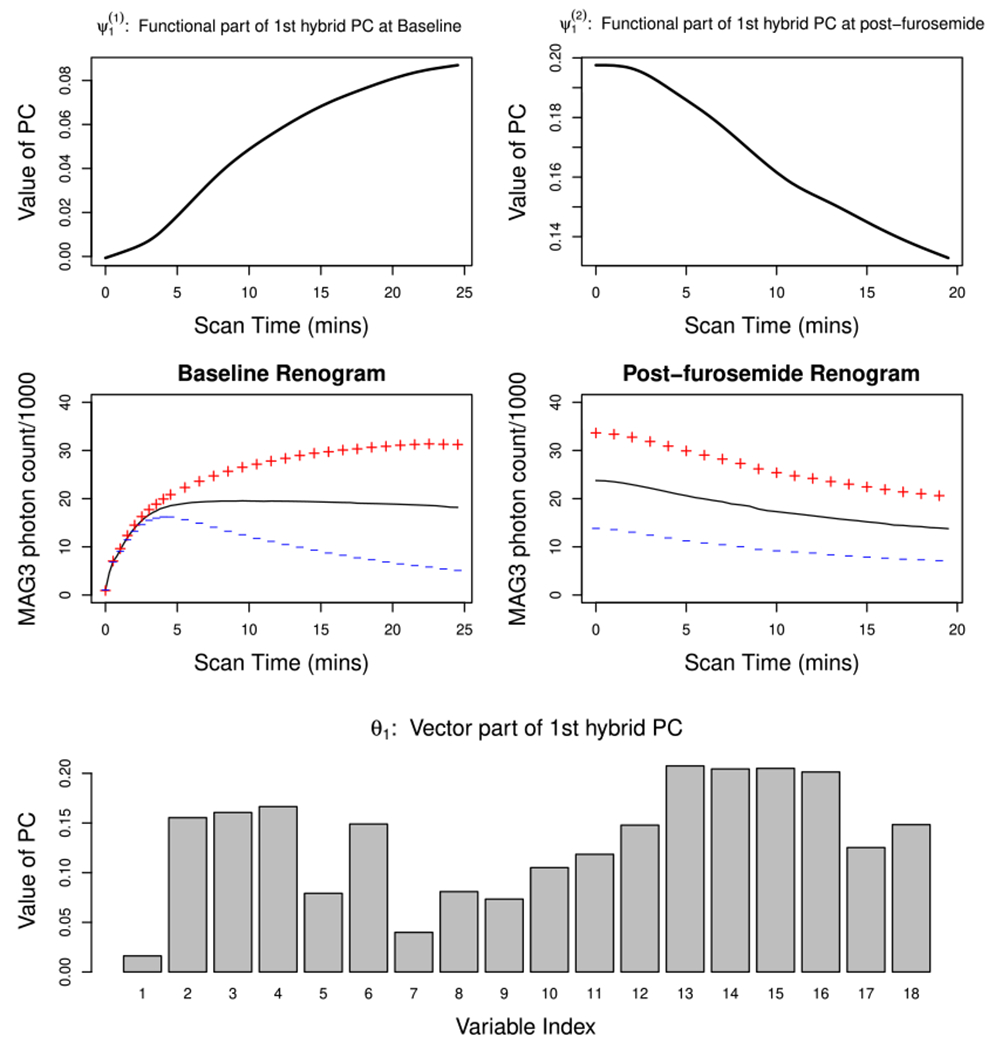
Estimated 1st hybrid PC ${\widehat{\xi }}_1$ of the Emory renal study data. The top panel represents the functional part of the estimated 1st hybrid PC: ${\widehat{\psi }}_1^{(1)}$ (left; baseline) and ${\widehat{\psi }}_1^{(2)}$ (right; post-furosemide. The middle panel plots the mean functions (solid line) and the effects of adding (+) and subtracting (−) a suitable multiple of ${\widehat{\psi }}_1^{(1)}$ (left) and ${\widehat{\psi }}_1^{(2)}$ (right). The bottom panel is the barplot for the vector part of the estimated 1st hybrid PC θ₁. [Colour figure can be viewed at wileyonlinelibrary.com]

Figure 3 depicts the second estimated hybrid PC, ${\widehat{\xi }}_2=\left({\widehat{\psi }}_2^{(1)},{\widehat{\psi }}_2^{(2)},{\widehat{\theta }}_2\right)$, which explains 17% of the total variability in the data. The top left and right panels, respectively, present ${\widehat{\psi }}_2^{(1)}$ (second baseline PC) and ${\widehat{\psi }}_2^{(2)}$ (second post-furosemide PC). The middle panel shows a suitable multiple of these PCs added (+) or subtracted (−) from the mean functions at baseline (left panel) and post-furosemide (right panel) periods. Kidneys with high negative scores on this component would display higher MAG3 level throughout the baseline period, but at the same time exhibit a faster washout during the post-furosemide period. On the other hand, those with high positive scores would display a relatively low MAG3 level that persists throughout the entire renal scan period without much drainage. ${\widehat{\psi }}_2^{(1)}$ and ${\widehat{\psi }}_1^{(2)}$ thus differentiate between kidneys according to the degree of discrepancy in the MAG3 level accumulated at baseline and that remaining at the end of the scan. Accordingly, the vector part of the second hybrid PC, depicted in the bottom panel, has negative loadings on renogram variables representing pharmacokinetic properties of the post-furosemide renogram and positive loadings on others, characterizing the variation of MAG3 level along a contrast between baseline and post-furosemide periods.

FIGURE 3.

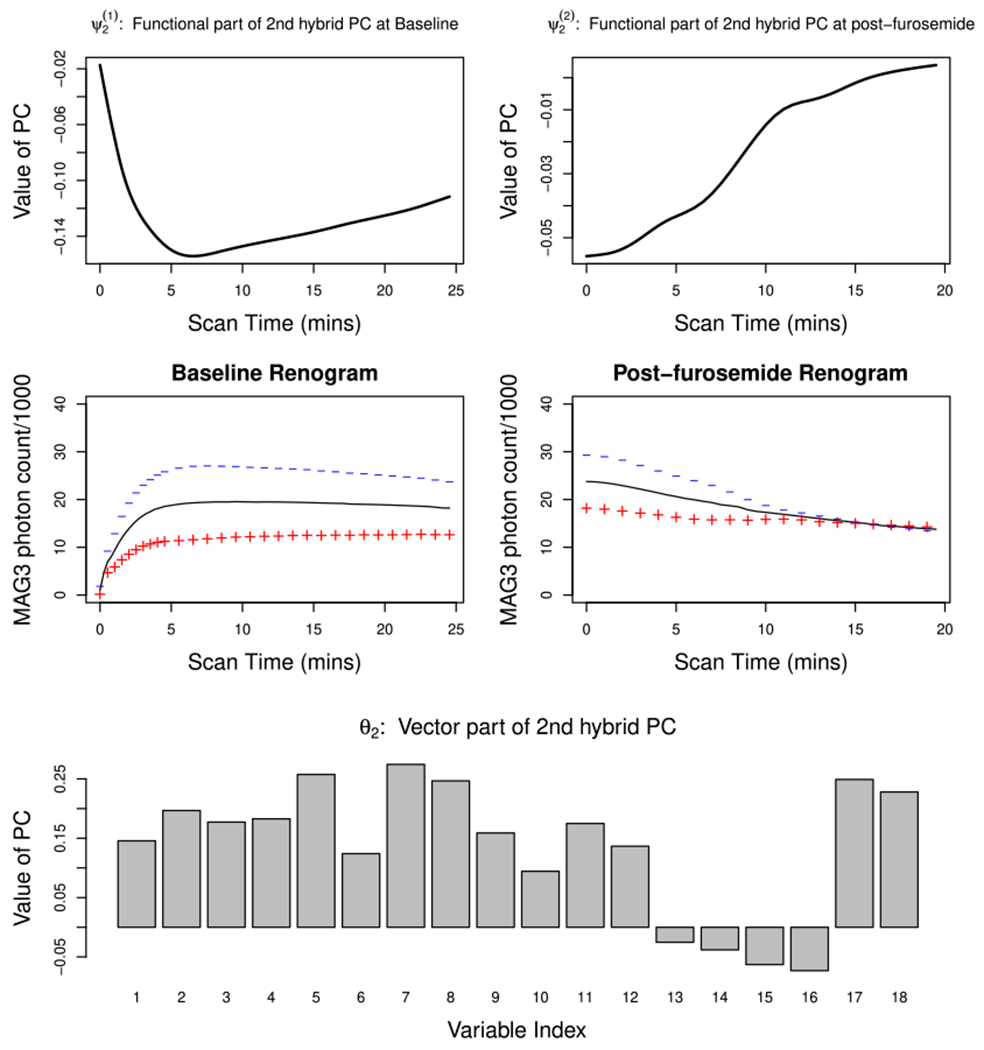
Estimated 2nd hybrid PC ${\xi }_2$ of the Emory renal study data. The top panel represents the functional part of the estimated 2nd hybrid PC: ${\text{Ψ}}_2^{(1)}$ (left; baseline) and ${\text{Ψ}}_2^{(2)}$ (right; post-furosemide. The middle panel plots the mean functions (solid line) and the effects of adding (+) and subtracting (−) a suitable multiple of ${\text{Ψ}}_2^{(1)}$ (left) and ${\text{Ψ}}_2^{(2)}$ (right). The bottom panel is the barplot of the vector part of the estimated 2nd hybrid PC θ₂. [Colour figure can be viewed at wileyonlinelibrary.com]

Finally, a scatterplot of estimated first and second hybrid PC scores of 253 kidneys is shown in Figure 4. The kidneys are grouped into three categories according to the consensus diagnosis provided by three internationally renowned experts in nuclear medicine: unobstructed (184 kidneys; 72%), equivocal (9 kidneys; 4%), and obstructed (60 kidneys; 24%). First hybrid PC scores are nearly all positive for kidneys diagnosed with renal obstruction, while those of kidneys that are unobstructed are mainly negative. Such a finding is consistent with the interpretation of the first hybrid PC provided above. On the other hand, the second hybrid PC scores do not differ notably by the obstruction status. One interesting observation on this component is that the kidneys that were diagnosed as “equivocal” by the expert panel have large positive scores, suggesting that physicians generally have difficulty interpreting the renal scan that shows neither apparent uptake nor apparent drainage of MAG3. Thus, more clinical research is warranted to study the implications of such a pattern on short-/long-term renal function. In conclusion, the results show that HFV-PCA can capture important source of variation in the renal study data that have meaningful interpretations tied to the underlying physiological mechanism of renal obstruction.

FIGURE 4.

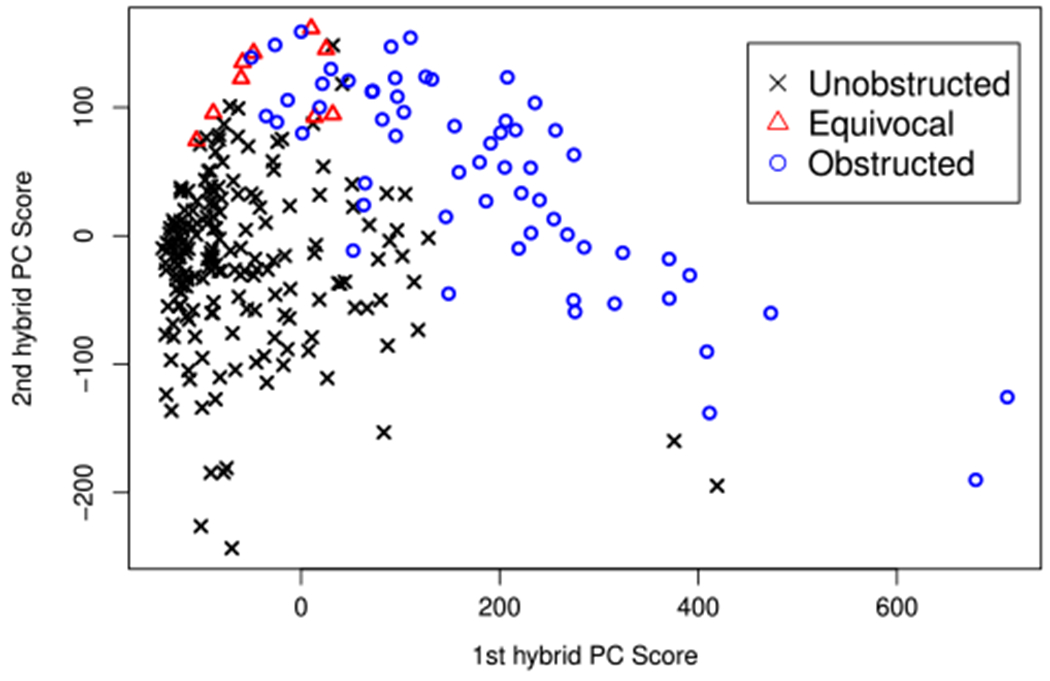
Scatterplot of first and second hybrid PC scores of 253 kidneys. [Colour figure can be viewed at wileyonlinelibrary.com]

5 |. CONCLUSION

This paper introduces a novel PCA framework that provides an efficient and parsimonious means to jointly model functional and vector data, while fully leveraging their simultaneous variations and co-varying patterns. The theoretical foundation of the framework builds on a Hilbert space that combines functional and vector objects as a single hybrid object and admits a covariance operator whose eigen-decomposition represents major modes of joint variation between the two data modalities. For practical implementation, a stochastic Karhunen-Loéve representation of a hybrid object is derived, and its analytic relationship with the functional and vector PC decompositions is established, enabling a fast and robust estimation scheme where components of HFV-PCA are computed based on separate FPCA and classical PCA counterparts. In application to renal study data, the proposed HFV-PCA leads to interesting insights into co-varying patterns of renogram curves and variables that are related to the mechanisms underlying renal obstruction. The proposed method thus shows promise for the analysis of modern clinical studies in which different data modalities are collected for each experimental unit. Further research may focus on extending the proposed method to incorporate a wider variety of modern data modalities including tensors and shapes.

DATA AVAILABILITY STATEMENT

The dataset that supports the findings of this study is proprietary and confidential, and cannot be shared with the general public for subsequent research purposes. The authors do not have the permission to publish or share the raw data.