Figure - PMC

Skip to main content

An official website of the United States government

Here's how you know

Here's how you know

Official websites use .gov
A .gov website belongs to an official government organization in the United States.

Secure .gov websites use HTTPS
A lock ( ) or https:// means you've safely connected to the .gov website. Share sensitive information only on official, secure websites.

View full-text article in PMC

. 2022 Feb 24;28(5):934–938. doi: 10.1038/s41591-022-01736-z

Search in PMC
Search in PubMed
View in NLM Catalog
Add to search

© The Author(s) 2022

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.

PMC Copyright notice

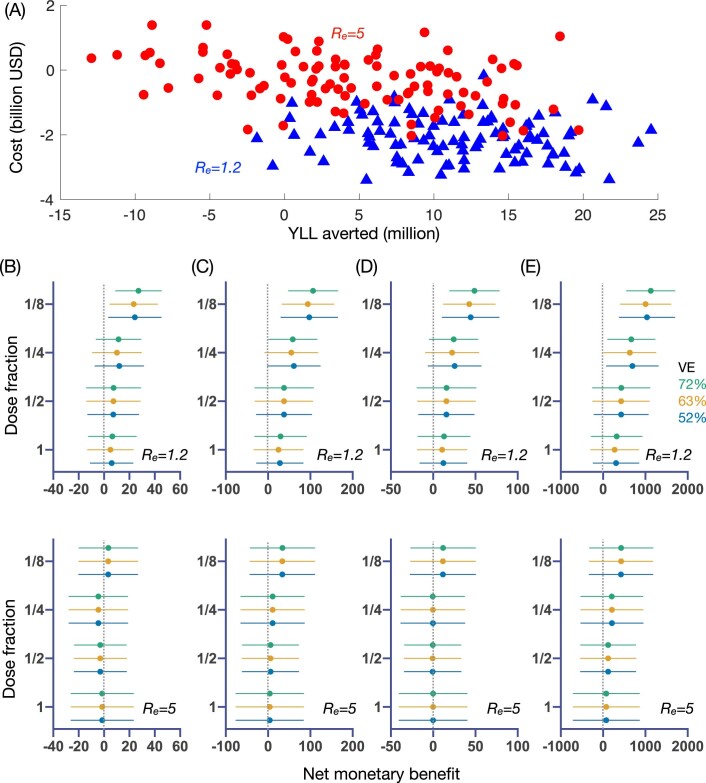
Extended Data Fig. 2 — (A) An example for the estimated costs of fractionated dose strategies versus the averted years of life lost (YLLs) with reference to the no vaccine strategy. Each dot indicates one realization of the 100 stochastic simulations, given the use of 1/8 dose fractionation strategy with 72% vaccine efficacy against infection (VE) (blue triangle and red circle indicate the estimates given effective reproductive number R_e = 1.2 and 5, respectively) and willingness to pay (WTP) per YLL averted of US$1,097, US$1,251, US$2,977, US$3,150, and US$3,205 for five age groups (0-5, 6-17, 18-49, 50-64, and > 65), respectively. (B) Estimated distributions for the expected gain in the NMB (2021 $ billion) over various vaccine efficacy against infection and fractional-dose strategy, given vaccine cost of US$12 and willingness to pay (WTP) per YLL averted of US$1,097, US$1,251, US$2,977, US$3,150, and US$3,205 for five age groups (0-5, 6-17, 18-49, 50-64, and > 65), respectively. Dots and error bars indicate the estimated mean and standard deviations, respectively. Colour scheme corresponds to the vaccine efficacy against infection. (C) Same as (B) but setting the WTP per averted YLL as US$10,517. (D) Same as (B) but setting the WTP per averted YLL as US$5089 (i.e., as in other middle-income countries such as Thailand). (E) Same as (B) but setting the WTP per averted YLL as US$100,000 (i.e., as in high-income countries such as theUS). Each subpanel in (B) to (E) uses 100 stochastic realizations to simulate theCOVID-19 transmission over each possible vaccine efficacy against infection (between 52% and 72%) and transmissibility (with effective reproduction number Re = 1.2 or 5). The optimal strategy given each transmission scenario is always estimated to be strategies with higher-fold fractionations, even if the vaccine efficacy against infection is not high. See Methods for the calculation of the NMB and supplementary materials for detailed values of vaccine costs and efficacy parameters.