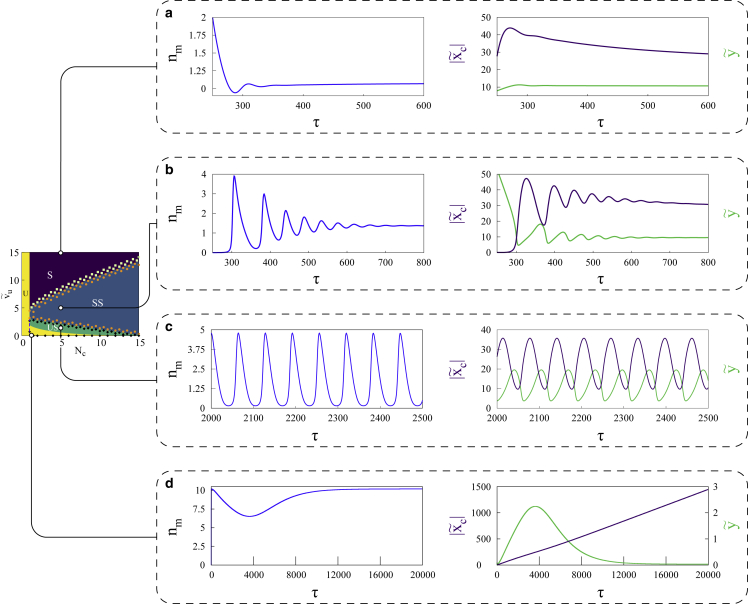
Figure 4.

Dynamics of the active system: numerical solutions of the dynamical equations at different points in the $N_c-{\tilde{v}}_u$ phase plane elucidate the dynamical phases predicted by linear stability analysis. The range of ${\tilde{v}}_u$ is equivalent to 0–9 μm/s, in physical units. At high ${\tilde{v}}_u$ region (a), the system is quickly stabilized as it reaches steady-state solutions, while relatively lower ${\tilde{v}}_u$ at (b) ensures that the system follows a path of decaying oscillations. It is at (c) that the system showcases self-sustaining limit cycle oscillations after crossing the supercritical Hopf bifurcation boundary. As predicted by linear stability analysis, critically low values of ${\tilde{v}}_u$ and $N_c$ ensure that the system is unstable, as evident by runaway clutch deformation. The range of extensions are equivalent to 0 to 70–88 nm in the first three plots. In (d), $x_c$ ranges within 0–2,650 nm, while y remains between 0 and 5 nm. Ranges of time in physical units are 0.6–1.7 s in (a), 0.6–2.3 s in (b), 5.7–7.1 s in (c), and 0–57 s in (d). To see this figure in color, go online.