Abstract
Job rotation is a work organization strategy with increasing popularity, given its benefits for workers and companies, especially those working with manufacturing. This study proposes a formulation to help the team leader in an assembly line of the automotive industry to achieve job rotation schedules based on three major criteria: improve diversity, ensure homogeneity, and thus reduce exposure level. The formulation relied on a genetic algorithm, that took into consideration the biomechanical risk factors (EAWS), workers’ qualifications, and the organizational aspects of the assembly line. Moreover, the job rotation plan formulated by the genetic algorithm formulation was compared with the solution provided by the team leader in a real life-environment. The formulation proved to be a reliable solution to design job rotation plans for increasing diversity, decreasing exposure, and balancing homogeneity within workers, achieving better results in all of the outcomes when compared with the job rotation schedules created by the team leader. Additionally, this solution was less time-consuming for the team leader than a manual implementation. This study provides a much-needed solution to the job rotation issue in the manufacturing industry, with the genetic algorithm taking less time and showing better results than the job rotations created by the team leaders.
Keywords: Automotive industry, Musculoskeletal disorders, Prevention approach, Workplace intervention, Genetic algorithm, Occupational risk factors
Highlights
-
•
This is the first formulation to consider diversity, exposure, and homogeneity.
-
•
A GA was used and proven to be a reliable solution to design job rotation.
-
•
The formulation increased diversity, decreased exposure, and balanced homogeneity.
-
•
Better results were achieved in all outcomes when compared with manual solutions.
-
•
The formulation is less time-consuming improving factory resource's management.
Automotive industry; Musculoskeletal disorders; Prevention approach; Workplace intervention; Genetic algorithm; Occupational risk factors.
1. Introduction
Musculoskeletal disorders (MSD) are the most common work-related health problem worldwide (Sebbag et al., 2019), being considered one of the top reasons for work absenteeism (Durand et al., 2014). Within this context, work-related musculoskeletal disorders (WRMSDs) have a significant impact on the declined working capacity and quality of life of workers, as well as high costs for companies and society due to productivity loss and healthcare services (De Kok et al., 2019). Preventing WRMSDs is especially important in repetitive jobs with less exposure variation, fewer breaks, and prolonged low-level exertions, such as that in the automotive industry (Mossa et al., 2016), since these jobs tend to be the reason behind the higher number of WRMSDs on the long term (Aryanezhad et al., 2009).
Alongside other measures to reduce the incidence of WRMSD (i.e. engineering, processes, and product changes on the assembly line), the job rotation plans have been recommended as an organizational measure to reduce the exposure in workplaces to several risk factors and, thus, increase the variability and reduce worker fatigue and monotony (Jorgensen et al., 2005; Rodriguez and Barrero, 2017; Yung et al., 2012). Within the several solutions found in the literature to optimize job rotation plans, there are mixed-integer programming to upper extremities (Boenzi et al., 2013; Digiesi et al., 2018; Xu et al., 2012), minimizing net present cost within a lean manufacturing cell (McDonald et al., 2009), multi-criteria fuzzy-genetic algorithms for assembly line balancing (Rajabalipour Cheshmehgaz et al., 2012), and diploid genetic algorithm (GA) in dynamic environments (Bhasin et al., 2016).
The GA stands out from the remaining solutions since it can solve complex mathematical problems in situations where there are a large number of possible outcomes and the environments are dynamic (Carnahan et al., 2000). In fact, the GA have already been implemented in different automotive industry scenarios with several studies using this approach to reduce the risk of MSDs and maximize the diversification of the job rotation plans (Asensio-Cuesta et al., 2012a, 2012b; Diego-Mas et al., 2009). For instance, the GA solution provided by Diego et al. for an automotive parts supplier assembly plant (Diego-Mas et al., 2009), focused on maximizing the diversification while using a multi set of criteria that characterized the workplace by physical, mental, and communication capacities. The same authors also used a GA approach to design a job rotation in environments characterized by high repeatability of movements (Asensio-Cuesta et al., 2012a). Compared to their previous work, authors added information from the Occupational Repetitive Action (OCRA) screening tool, in which they assessed the presence of risk factors when performing repeated movements. The solution was able to diversify the tasks in order to aid the recovery of workers in between jobs. In a different take on this topic, Asensio-Cuesta and colleagues (Asensio-Cuesta et al., 2012b) developed another GA solution that considered the competence criterion related with product quality and employee satisfaction as a measure for the goodness of solutions. Although the method used is the same, the choice, the number, and the diversity of variables included in the model (e.g. movements, general capacities, task time) as well as the criteria used to establish the GA (e.g. capacity to perform the movement, frequency of movement per minute) differ between studies, which leads to different results and amplifies the lack of consensus in the literature regarding the effectiveness of rotation plans (Comper and Padula, 2014).
Although most of the studies have focused on the issue of diversity for the development of the job rotation plans, other criteria may have a significant impact in reducing the risk of MSDs, and should not be overlooked, such as the homogeneity (i.e. balanced effort) between workers and the overall exposure (i.e. daily demand) to risk factors. Moreover, the majority of the GAs used in the literature relied on changes in the intensity of the task to increase the diversity of the job rotations, which was achieved by using specific or general ergonomic risk assessment metrics, differing in respect to the level of detail regarding evaluation sections they cover (Carnahan et al., 2000; Diego-Mas et al., 2009). Moreover, most of the studies covered the issue of job rotation plans in an automobile parts supplier industry, with a lack of information on assembly lines of big automotive plants, where the specificities of the tasks performed may have different implications for WRMSDs. To the best of our knowledge, currently there is no suitable solution to tackle the job rotation issue in the automotive industry that focuses not only on the diversity criteria, but also ensures the reduction of exposure throughout the working shift, and safeguards the homogeneity within the team, while using objective ergonomic indicators to build a job rotation plan.
This study's aims were two-fold: 1) to develop a formulation based objective ergonomic indicators and workers qualifications to generate a job rotation plan based on diversity, homogeneity, and exposure criteria for an assembly line in the automotive industry, solved by means of a GA; and 2) provide an industrial case study where the GA was tested and applied to a randomly selected team from the automotive assembly area in a real life-environment, in order to compare the performance of the job rotation plan formulated by the new GA versus that of the team leader.
Given the length and detail of the GA, and to guide the reader, the manuscript is organized in to the following sections: In section 2, we address the modelling assumptions used to apply the GA, provide a detailed description of the job rotation variables included in the GA and explain the respective mathematical formulation. In section 3, we describe the GA architecture and the several steps needed to provide the best closing condition. Section 4 presents the results of an industrial case study, where the GA was tested in a real life-environment. Finally, in section 5, the results are discussed and wrapped up by a conclusion in section 6.
2. Methods
2.1. Modelling assumptions
To apply the GA in this study, several assumptions were considered, including organizational conditions, workforce, and workstation characteristics, which were made to cope with real-life environments constraints of this assembly line, including:
-
•
Workers perform the workstations that they are qualified to, according to the versatility matrix of the respective team.
-
•
In each rotation period, only one workstation could be assigned to each worker.
-
•
During a shift, the same workstation should not be assigned to a worker more than once.
-
•
Workstations with high demands on the same body region should not be consecutively assigned to the same worker.
-
•
Any workstation can be assigned in the first period of the shift, as full recovery from one day to the next is assumed.
-
•
All variables of the formulation are deterministic and constant during the planning horizon.
-
•
The allocation of workers to workstations is independent of gender, efficiency, and quality.
2.2. Notation
The notation used in the proposed model is available in Table 1. In Table 2, the risk factors and respective abbreviations are presented.
Table 1.
Index and parameters definition.
| Index | Definition |
|---|---|
| Index of workstations, where = 1,2,…, | |
| Index of workers, where = 1,2,…, | |
| Index of rotation periods, where = 1,2,3,4 | |
| Index of categories of each risk factor or risk factor layers, where = 1,…, | |
| Index of layers of the force risk factor categories, where = 1,2,…, | |
| Index of the workplace transition period, where t = 1,2,…, | |
| Index of risk factors of the EAWS, where = or | |
| Parameters | |
| Score of a workstation on a rotation period (See Eq.1) | |
| Overall score of a workstations | |
| Percentage of time of rotation period | |
| Occupational exposure score of a sequence of workstations attributed to a worker (See Eq.2) | |
| Normalized occupational exposure score of a sequence of workstations attributed to worker (See Eq.3) | |
| Minimum occupational exposure score of worker | |
| Maximum occupational exposure score of worker | |
| Transition score of the risk factor group A (e.g. - posture and - Manual Material Handling) for the transition period (See Eq.4) | |
| Transition score given to the category of the risk factor (group A) for the transition period | |
| Transition score of the risk factor group B ( - force) for the transition period | |
| Transition score given to the layer of the risk factor (group B) for the transition period (See Eq.5) | |
| Transition score given to the layer and category of the risk factor (group B) for the transition period | |
| Transition score of a sequence for risk and worker (See Eq.6) | |
| Transition score for the transition period | |
| Transition score of a sequence for worker (See Eq.7) | |
| Weight of risk factor | |
| Standard deviation of the scores of the team (See Eq.8) | |
| Standard deviation of the scores of the team (See Eq.10) | |
| Mean score for the team | |
| Mean transition score of the team | |
| Shift working sequence quality for worker (See Eq.13) | |
| Mean shift working sequence quality (See Eq.14) | |
| Homogeneity score (See Eq.12) | |
| Homogeneity score for diversity | |
| Homogeneity score for occupational exposure | |
| Matrix quality index of the job rotation plan (See Eq.15) |
Table 2.
Risk factors and abbreviations.
| Risk factor | Definition |
|---|---|
| p | Posture |
| NS | Neck and shoulders |
| T | Trunk |
| E | Elbow |
| MMH | Manual Material Handling |
| Rep | Repositioning |
| Car | Carrying |
| Hold | Holding |
| Pu | Push and Pull |
| f | Action forces |
| WB | Whole body |
| HF | Hand and fingers |
| SL | Arms at shoulder level |
| ASL | Arms above shoulder level |
| B | Trunk bent |
| SB | Trunk strongly bent |
| GA6 | Elbow at 60% extension |
| GA8 | Elbow at 80% extension |
| GA10 | Elbow at 100% extension |
2.3. Job rotation plan variables
Two main types of variables were considered to design the job rotation plan: (1) biomechanical variables; and (2) organizational variables.
2.3.1. Biomechanical variables
The main variables used to define the quality assessment of a job rotation schedule were: (1) the overall risk score of each workstation, resulting from the assessment of the biomechanical and organizational work conditions; (2) the duration and intensity of the biomechanical risk factors present in each workstation such as posture, force and manual material handling (MMH).
Data on biomechanical work conditions (intensity, duration and frequency) were collected from the ergonomics evaluation made through the Ergonomics Assembly Worksheet method (EAWS) (Schaub et al., 2013) performed by certified ergonomists. The corresponding methods evaluated the movements made by a worker while performing the workstation. This method assessed:
-
•
working postures and movements with low additional physical efforts;
-
•
action forces of the hand-finger system and/or whole body;
-
•
MMH;
-
•
repetitive loads on the upper limbs.
As a result, a combined score of all these risk factors was used and an overall exposure score was assigned to the workstation characterized by a traffic light colour scheme: green - no risk or low risk (0–30 points); yellow - possible risk (31–49 points); and red - high risk (>50 points) (Schaub et al., 2013).
2.3.2. Organizational variables
The team's versatility matrix was obtained from the Team Leader. The matrix indicates the qualifications of workers. In other words, it provides which workstations can be assigned to which workers according to their skills. The duration of each rotation period differs between shifts (early, late, and night shifts) and even between teams within the same area. Also, a common approach in practice is to estimate ergonomic risks as a time-weighted average of the respective ergonomic points for the different jobs. Thus, this data was also included to calculate the occupational exposure score for the quality assessment metric.
2.4. Defining the fitness function
The fitness function is the core of this work. In this function, the mathematical formulation that guides optimization algorithms, such as the GA, was integrated to reach the solutions that were desired. In this section, we describe how this mathematical formulation was created based on the aforementioned variables.
The quality of the job rotation schedule was estimated with variables that are present in the working day of each worker. The EAWS data was used to characterize the occupational environment. These scores quantify the risk of each workstation and provide an individual picture of each of the risk factors that were used for the global score. The way these variables are combined to give a representative score of the job rotation schedule should maximize its purpose, which is to assign a sequence of workplaces that promotes the variation in posture, load, and muscle activity (Mathiassen, 2006).
Furthermore, the proposed mechanism for building the fitness function was composed of three layers of analysis: (1) overall averaged occupational exposure score, (2) diversity calculated for the sequence of workstations considering the risk factors, and (3) a homogeneous rotation schedule, so that the scores assigned to the team were balanced between workers.
2.4.1. Exposure
The first layer of assessment involved calculating the average occupational exposure score from the sequence of workstations assigned to each worker. The occupational exposure score of a workstation () in a given rotation period rot was calculated according to Eq. (1), considering the network shift time:
| (1) |
The time was fixed according to the rotation period in which the workstation was allocated. Finally, the resulting score for a sequence of workstations () performed by a worker over the set of rotation periods ( =4) was given according to Eq. (2):
| (2) |
The has to be normalized to obtain a value between 0 and 1 as an output. A sequence with a score of 0 was the best possible sequence of workstations considering the qualification matrix. On the other hand, the score of 1 represents the worst possible sequence of workstations. The lowest exposure score () was therefore associated with 0, while the highest () was associated with 1. Before the algorithm was applied, the worst and best reference exposure sequences for each worker were calculated. The normalization was made taking into consideration these reference values ( and ):
| (3) |
where was the normalized occupational exposure score for a given worker's () sequence.
2.4.2. Diversity
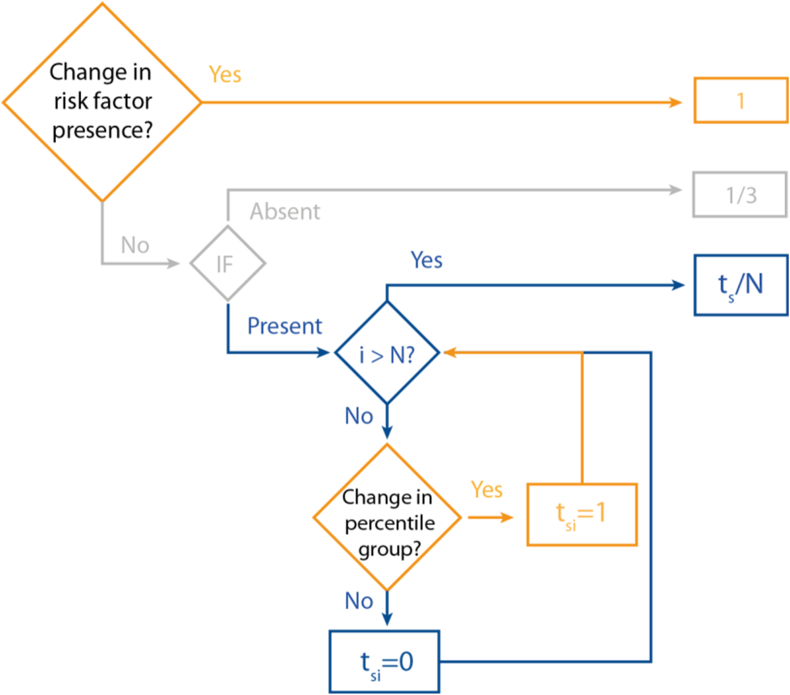
The second layer of assessment consisted of calculating the diversity in the sequence of workstations. Diversity is the amount of change in the exposure score between successive workstations for each one of the following risk factors: posture, force, and MMH. Therefore, this measure should guide the algorithm to reach solutions that have a high diversity. Generally, diversity was calculated through a score for the transitions between categories of exposure in successive workstations (in a multi-layered process). It is relevant to mention that the term transitions was intended to represent the change in the presence of a risk factor between successive workstations. Since there were 4 working periods, there were 3 transitions evaluated. Independent of the risk factor, each transition can be categorized, based on the presence (1) or absence (0) of a risk factor, as one of the three possible types of transitions showed in Figure 1, namely Type 1, 2 or 3:
Figure 1.
Diversity in posture and manual material handling. The process is depicted as a flowchart. When the risk factor is present in both workstations, the process iterates over the categories of the risk factor, being the iterator variable.
Type 1 transitions - there is a change between the presence and absence of risk factor in two consecutive workstations (presence to absence, or vice-versa). The score for this transition is 1, as it is the type of transition preferred to be searched.
Type 2 transitions - the risk factor is absent in two consecutive workstations, so the score is ⅓ (absence to absence). This value was given because the absence of a risk factor in two consecutive workstations should not be evaluated as bad, but the algorithm should be guided in searching for solutions that have diversity, therefore it should be scored under 1. This way, type 2 transitions are favoured against type 3 transitions, but not with regard to type 1 transitions.
Type 3 transitions - the risk factor is present in two consecutive workstations, thus being the non-desirable transition. The score attributed to this type of transition was dependent on the risk factor evaluated.
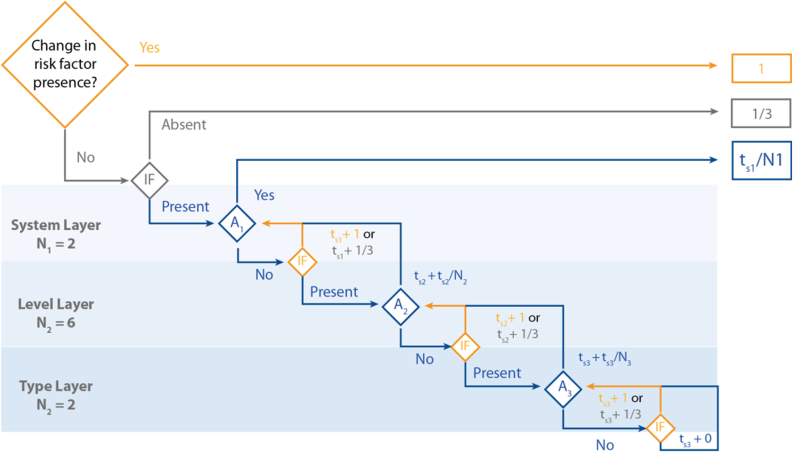
The process to calculate the score of a transition depends on the risk factor category. For posture and MMH, the process is showed in Figure 1, while for force, the process is showed in Figure 2.
Figure 2.
Flowchart to calculate force diversity. In each layer, on the left, it is indicated the number of categories (N). On the right side, the possible scores attributed to type 1 (top), type 2 (middle), and type 3 (down) transitions are presented.
Diversity in posture and manual material handling
The diversity in posture and MMH was calculated following the same rationale. The first step was to verify the presence of a risk factor in the next workstation. Therefore, if the risk factor was present in the first workstation (1) but not in the next one (0) (or vice versa - type 1 transitions), then the score for the transition was calculated for the risk factor between these two workstations was 1. However, if the risk factor was absent in both (type 2 transitions), then the transition score was 1/3. If the risk factor was present in the first two workstations, which means that no transition existed, then a second step was needed.
EAWS evaluates posture according to time spent in an awkward posture during the cycle time. A transition in the sequence would mean that the difference in the scores of the following workstations was significant. To establish significance levels, the distributions of the risk factor scores for each posture category, and each worker were divided into four percentiles (0–25%, 25–50%, 50–75%, and 75–100%). Transitions were considered significant when consecutive workstations had scores belonging to different percentiles. If there was a change in the percentile, the score was 1, and if not, the score was 0. Although the body region was recruited in two consecutive workstations, the intensity with which this recruitment took place was different, and, therefore, there was diversity. This diversity was sought with this algorithm.
The process to calculate the diversity score for MMH was the same as posture. In the case of posture, a diversity score for each body region (N = 3) (i.e. elbow, trunk, and shoulder/neck) was calculated. In the case of MMH, 4 categories (N = 4) were considered: repositioning, carrying, holding, and pushing and pulling.
Equation 4 shows the process to calculate the transition score () for posture and MMH:
| (4) |
Here, the is the score for the transition of the risk factor; represents the categories of the risk factor; is the score for the transition and the category for the risk factor (body region and MMH categories), and is the percentile where the workstation on the rotation period belongs to, with being the percentile belonging to where the workstation is on the next rotation period . To have an output between 0 and 1, a denominator factor was used, which is equal to the number of categories in each factor.
Diversity in force
The calculation of diversity in force follows the same logic as in the previously mentioned risk factors. However, when facing a transition of type 3, the process was made in more layers and differently. The first step, like posture and MMH, was checking if a risk factor was present in consecutive workstations and if so, the following layers were evaluated: (1) the presence of that risk in one or both systems “whole-body” and/or “hand-arm-finger”; (2) if present, at what intensity and, (3) in what type, dynamic or static. Figure 2 represents the calculation of diversity for force.
Looking at Figure 2, the rationale followed in a downward direction until the transition was verified or until the last layer was met (the type of force).
In the case of being present in two consecutive workstations, the score was calculated in the next layer to verify the change in the presence or absence of the risk factor in the whole body or hand-arm finger system. Next, the process was repeated, and if the risk factor was presented in both workstations in the system layer, the presence and absence of the risk factor was checked for each intensity level (light, medium, high, stressed, maximum, or > maximum). If the risk factor was observed in both workstations at a specific intensity level, the calculation of the score goes deeper and the change of presence and absence of the risk factor was evaluated for the force mode (dynamic or static). Finally, in that layer, if the presence of the risk factor was verified in both workstations, then the output was 0.
The details in Eq. (5) show how to calculate the diversity in force:
| (5) |
In this case, is the transition score given to layer , is the transitions score for the category in that layer . is the number of categories of layer and is the iterator over the categories.
2.4.3. Total diversity score
For each one of the risk factors described in the previous sections, the transition score had to be accounted for all rotation periods during the working day. Therefore, the diversity score of each risk factor was calculated with Eq. (6):
| (6) |
Note that, is the transition score for risk factor for worker in the transition period , resulting from the sum of the transition score for the transition period .
The total diversity score, considering all risk factors was calculated. As the effect of the risk factors on occupational exposure was not equal, the relevance of the transition score of each risk factor was weighted () differentially: 3 for posture, 2 for force, and 1 for MMH. The rationale for this choice was based on the ergonomics assessment and the weight of each risk factor to the total score (Bao, 2015). The score of each change in the workplace was then the sum of the transition score for each risk factor normalized between 0 and 1. The final score value was calculated according to Eq. (7):
| (7) |
In this formulation, is the risk factor considered: posture, force, or MMH.
2.4.4. Homogeneity
The homogeneity was the last variable included in the fitness function, and our formulation. In order to guarantee the balance between the team, homogeneity aimed to guide the algorithm to avoid favouring workers differently. The homogeneity score was calculated after the occupational exposure and diversity score were calculated for all of the team workers. The standard deviation of occupational exposure (Eq. 8) and diversity scores (Eq. 10) was calculated. Then, the homogeneity contribution of occupational exposure (Eq. 9) and diversity (Eq. 11) was determined.
| (8) |
| (9) |
where: the is the standard deviation of occupational exposure, is the number of workers on the team, is the iterator over the workers, is the occupational exposure score for the worker and is the mean occupational exposure score of the team. is the homogeneity contribution of the exposure.
| (10) |
| (11) |
Here is the standard deviation of occupational exposure, is the number of workers on the team, is the iterator over the workers, is the diversity score for the worker and is the mean diversity score of the team. is the homogeneity contribution of diversity.
Since the standard deviation is a measure of dispersion, the higher the value the worse the balance is of the job rotation plan between workers. As a mean to have a value with a positive trend (the higher the better), the homogeneity score () results from an inverse sum of both standard deviations. The final homogeneity score is given by Eq. (12):
| (12) |
2.5. Formulation of the fitness function
The fitness function is the combination of occupational exposure, diversity, and homogeneity. For each worker sequence, a score was calculated for occupational exposure and diversity, normalized between 0 and 1. The index that characterizes the quality of this worker sequence was the weighted sum of both scores, 2 for diversity, and 1 for occupational exposure (Eq. 13).
| (13) |
In this case, is the quality of the shift working sequence index for worker . Note that the occupational exposure score has a negative trend (the lower the better), therefore the subtraction in the equation was used to invert the trend of the parameter.
The shift working sequence quality (), which means the quality of the job rotation plan for the entire team (i.e. characterizes the job rotation plan in terms of occupational exposure and diversity), was calculated by averaging the set of indexes (Eq. 14).
| (14) |
Finally, the homogeneity score was added, resulting in the matrix quality index () (Eq. 15):
| (15) |
Since the search should favour job rotation schedules with reduced exposure and high diversity above homogeneous schedules, a weight of 0.25 was calculated for the homogeneity score to adjust its influence in the guidance of the algorithm.
The fitness function is then the MQ index, which has to be maximized to reach solutions that increase the diversity, reduce the exposure and increase homogeneity, as presented in Eq. (16):
| (16) |
3. Heuristic approach for job rotation scheduling
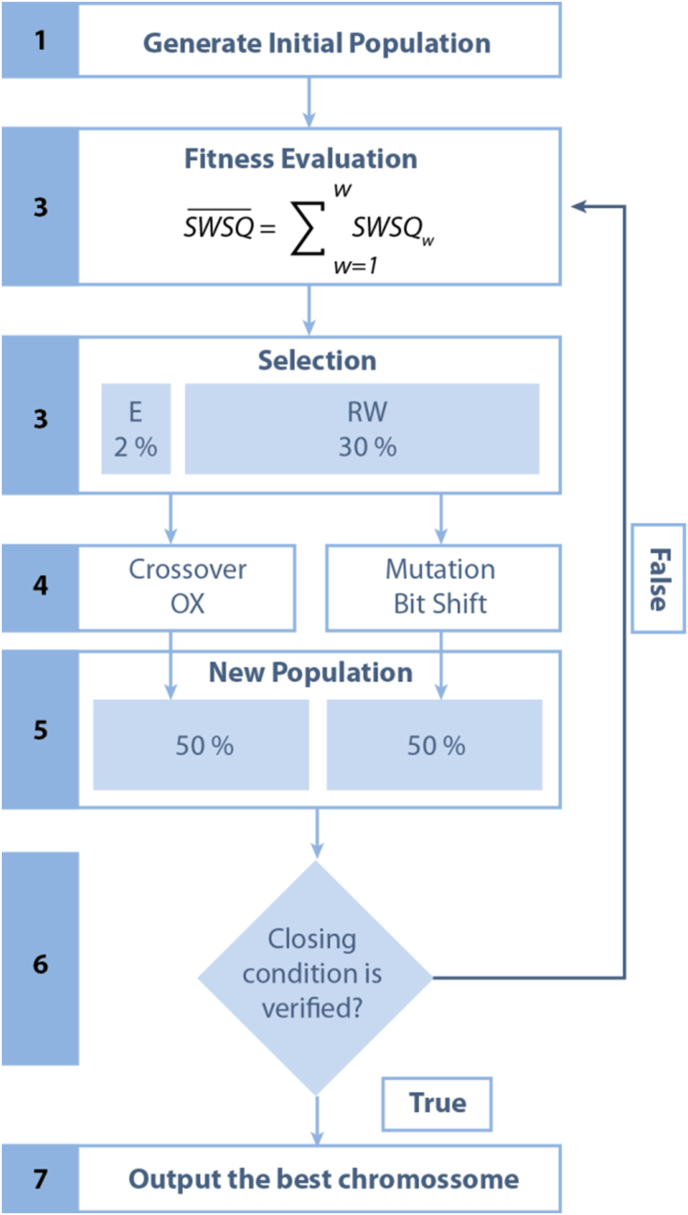
The fitness function (Eq. 15) represents the quality of the job rotation plan regarding occupational exposure, diversity, and homogeneity. This function guides the algorithm in generating a job rotation plan that maximizes the function (Eq. 16). From this formulation, any optimization algorithm can be applied to reach a desired solution. In this case, the proposed algorithm was based on a GA, which was already applied in similar contexts by Diego-Mas et al. (2009). In this section, we describe the several steps that comprehend the GA's architecture (Figure 3). The GA relies on the natural selection theory, in which evolution of the overall population into better offspring was expected over several iterations.
Figure 3.
Flowchart of the genetic algorithm architecture: Step (1): Creating initial population with valid chromosomes - randomly generated. Step (2): Evaluating the fitness of population members applying Eq. (13), which considers exposure, diversity, and homogeneity. Step (3): Selection of the individuals that will undergo crossover and mutation with 2% Elitism (E), 10% Tournament (T), and 30% Rank-Based Wheel (RW). Step (4): Apply Crossover and Mutation methods. Step (5): Generate an offspring population from the selected chromosomes. Step (6): If the closing condition is met, return the best offspring (Step 7), otherwise, return to step 2. Abbreviations: – Mean shift working sequence quality; - Shift working sequence quality for worker ; OX – ordered crossover.
The algorithm starts by generating the initial population. Thereafter, in each iteration, a selection of a set of chromosomes that belonged to the population pool were selected to perform a crossover with their genes and/or were mutated, expecting that better chromosomes would be created over the iteration process that ended when a closing condition was verified. The proposed genetic algorithm followed the same architecture.
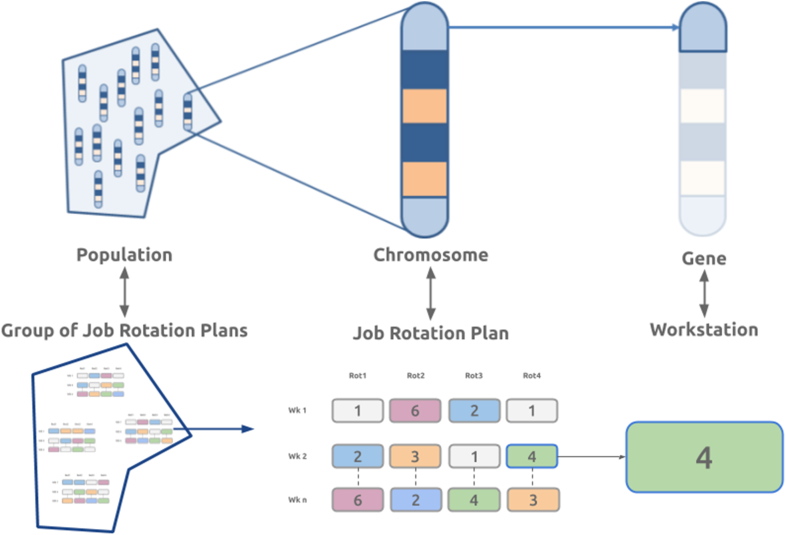
In this case, the nomenclature is defined in Figure 4, showing that the population is the overall set of possible job rotation plans; the chromosome belonging to the population is a valid job rotation plan; and the gene belonging to the chromosome is a workstation of the job rotation plan.
Figure 4.
Nomenclature of the genetic algorithm. The population is regarded as the group of possible job rotation plans; the chromosome is a valid job rotation plan and the gene is a workstation.
The way a GA is structured can vary extensively and several approaches were found in the literature for the selection, crossover, and mutation steps. The chosen methods depend on the type of problem itself and the restrictions that the problem implies. In this case, the main restrictions were related to the definition of a valid job rotation plan. The structure of the proposed algorithm will be explained further, namely which methods were used for the selection, crossover, and mutation, as well as what comprised was the closing condition.
3.1. Population generation
The GA started by randomly generating a primary population pool that contained a set of chromosomes. Each of these chromosomes is valid and cannot be generated against the constraints defined. Thus, a chromosome had a size of , with being the number of workers (equal to the number of workstations) and the number of rotation periods. One workstation was randomly assigned to each of the cells in the matrix, and no workstations was repeated on the same row. The initial number of chromosomes in the population can vary. The value of 100 individuals was considered, after obtaining satisfactory results for the case of 12 workstations and 4 rotation periods. Each of the chromosomes belonging to the population was evaluated by the fitness function to get a score that characterized their fitness.
3.2. Selection
Having the starting population, the next step was to select a set of chromosomes for the search space exploration with crossover and mutation. The selection had several criteria. The main idea was that the population should be able to evolve and chromosomes should have better scores over the iteration process. First, it was necessary to guarantee the presence of 2% of the best chromosomes of the population for the next iteration, a process called elite selection. Second, for this process, a rank-based roulette wheel selection (Goldberg, 1989) was used to select 30% of the population pool. It is important to note that a chromosome selected was excluded from the population set to avoid further repetitions in the selection.
3.3. Crossover
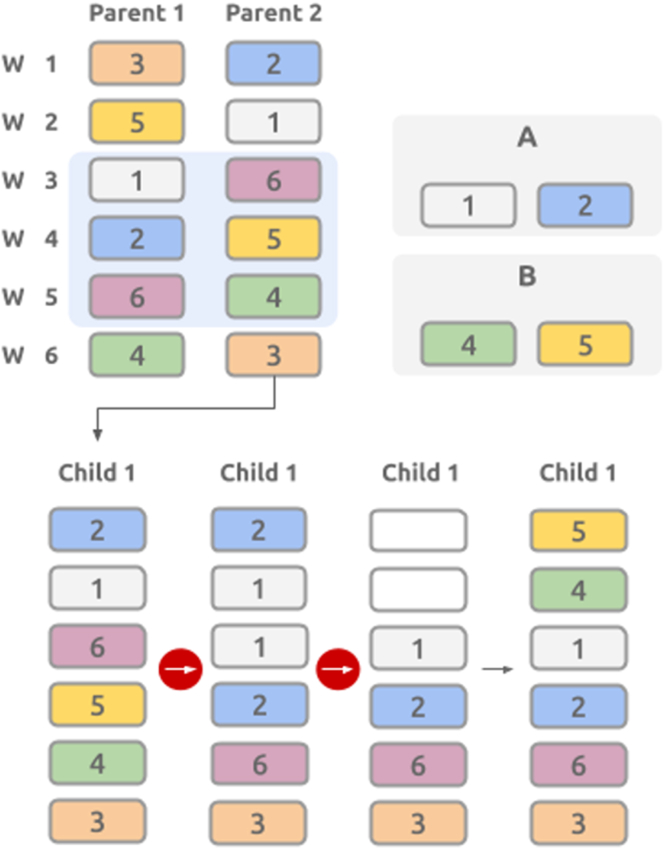
The selected chromosomes were the base individuals that origin the new population for the next iteration. The crossover was responsible for 50% of the new population. During crossover, the selected chromosomes were merged based on a specific method. When merging the information of two chromosomes, the sequences of workstations attributed to each worker based on the information of two job rotation plans was expected to be reorder. The problem in swapping information from one job rotation plan to the other was that the offspring would probably be invalid, because: (i) it would have repeated workstations on the same rotation period; and (ii) the workstations assigned to a worker might not be present in his/her qualification matrix. To tackle these constraints, the proposed solution was to use a permutation-based crossover method applied column-wise to the chromosomes. In this case, the method considered was the ordered crossover (OX) (Moscato, 1989). Consider the example presented in Figure 5. For this example, we assumed that there were six different workstations and six different workers. The colour and the corresponding number represent each workstation. The corresponding qualification matrix is presented in Figure 1 Supplementary Material.
Figure 5.
Example of the ordered crossover method applied to this problem. From two parents (one rotation of a job rotation plan for each parent) a child was created. The child was based on a variation of parent 2, which has received the selection from parent 1, in the same positions. The genes that were now repeated in the child (group A) are erased, and the ones that are not present in the child will be added by the order they appear in parent 2. For those who belong to the map, the shift of genes will go through a qualification check. The red points indicate the checkpoint because of the workstation shift. Abbreviations: w – worker.
From two job rotation plans ( and ), a random number of rotation periods (column) were selected to go through the OX method. From a column was selected as the first parent (, and the same column from was selected as the second parent (. The OX method starts by selecting randomly a subsection of workstations from . The child was mapped by inserting into , on the same subsection positions, the subsection of . In Figure 6, ; and were shifted from ; and . After that, the repeating workstations ( and - group A) were deleted from . The now missing workstations ( and - group B) were added by order of appearance in the original . This new rotation period was with ; ; ; ; and.
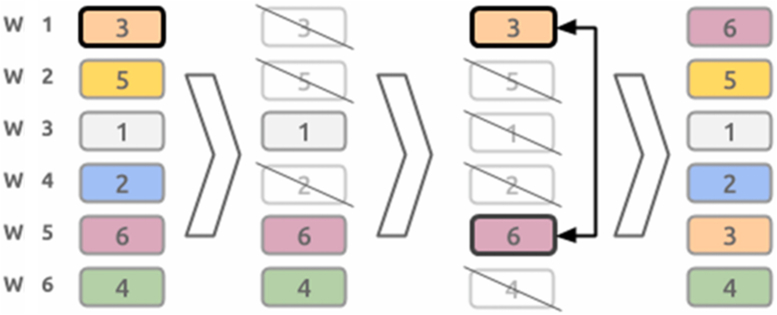
Figure 6.
Mutation example. A rotation period was selected and would be mutated to generate a variation of the rotation period. Abbreviations; w – worker.
Each row (worker) had a set of valid workstations. If during the OX method, a workstation was shifted into a row where it was not valid, the process searched for rows where this workstation could fit and made the exchange. This process was a checkpoint to ensure the child generated was a valid option.
3.4. Mutation
The mutation is the other operator used to generate the other 50% of the new population. The method used was a variation of the bit string mutation. The process comprised 3 steps and was done per column: (1) random selection of rotation periods; (2) random selection of a workstation for a given rotation period; (3) change of the workstation selected for another in the same period of rotation, as long as it ensures compliance with the qualification matrix.
Consider the example presented in Figure 6 and the qualification matrix (Figure 1 Supplementary Material). The example shows a column of one of the selected job rotation plans. The column had randomly been selected (step 1). Then one workstation was randomly selected (step 2). After that, this workstation was shifted with workstations that would follow the requirements. In this case, 3 from 1 was selected. The possible workers to shift this workstation with were 3, and 6, because these have 3 on their qualifications, and 1 is able to perform 3, 5 and 6. The shift workstation was then chosen randomly from the valid group.
3.5. Closing conditions
When the closing condition is reach, the iterative process of the genetic algorithm ends, and a result is returned. Two conditions must be met: (1) "is the score of the best chromosome higher than the reference value?" and (2) "is the number of iterations above 100?”. The first condition guarantees that a job rotation plan with a referenced adequacy was returned. The reference value was the mean score of the weekly job rotation plan designed by the team leaders for their URQ. The second condition was meant to give the algorithm enough iterations to stabilize. This value had to be experimentally calculated by running the algorithm 1000 times and extracting the value that ensures a good margin to let the algorithm stabilize. When these two conditions are met, the algorithm stops and outputs the best chromosome of the population. If the conditions are not met, the algorithm is kept running to improve the offspring.
4. Industrial case study
A full detailed example on how to the GA can be applied can be found in the Supplementary Material. The GA was also tested in a real life-environment, by being applied to a randomly selected team from the assembly area of an automotive industry with 12 workers, 12 workstations, and under the responsibility of (hereafter) a team leader. All workstations were close together and the standard rotation did not affect the normal operation of the production line (since rotation periods coincided with breaks). Although there was a standard job rotation at the company (provided by the Team Leader), the choice of the workstations was mostly based on empirical knowledge and experience.
In this study, the morning shift was considered. The working day was composed of 8h, with a lunch break of 30 min, and two breaks of 7 min each, before and after lunch. This translates into a mean network time of 466 min. Considering the network time, four working periods were already established with the following relative distributions: (1) 22.6%; (2) 30.7%; (3) 27.0%; and (4) 19.7%. Each worker performs 4 different workstations during the working day, according to their qualification. The versatility matrix was consulted to allocate workers to workstations that they were able to perform autonomously.
4.1. Workstations and workers
The evaluations of the 12 workstations belonging to the team are presented in Table 3. Most of the workstations were classified with medium risk, one workstation was classified as no risk () and two workstations were classified as high risk ( and ).
Table 3.
Ergonomic evaluation and risk factors characteristics. Risk factor scores for all categories of the EAWS. The colours on the Action Forces section represent the type of force exerted: black - dynamic and static forces; dark grey - dynamic forces; light blue – static force; light grey - the risk factor is not present. The unit %t indicates the percentage of time spent in that risk factor during 1 cycle time, and n represents the number of times these risk factors appear in 1 cycle time.
Abbreviations: Ws – Workstation; NS – Neck and shoulder; ASL – At/Above shoulder level; AHL – Above head level; T-Trunk; B-Bent; SB-Strongly bent; GA6 – Arm reach at 60%; GA8 – Arm reach at 80%; GA10 – Arm reach at 100%; MMH – Manual material handling; R – Repositioning; C – Carrying; H – Holding; P – Pushing and Pulling; WB – Whole body force; HAF – Hand Arm Finger force; S - Score. Note that posture was evaluated considering the percentage of time that an awkward posture was observed during the cycle time (approximately 79 s), as well as the static force for the whole body and hand arm finger systems. The dynamic type of force was accessed according to the frequency of its presence in the cycle time. The presence or absence of MMH in the workstation was used to classify this risk factor.
The team's qualification matrix is given in Table 4. From the 12 workers, eight had full versatility, i.e., they can perform autonomously all workstations, which was an advantage to the Team Leader.
Table 4.
Worker's versatility according to the workstations. The empty cells indicate that the worker does not have the competence to perform the respective workstation.
| WS1 | WS2 | WS3 | WS4 | WS5 | WS6 | WS7 | WS8 | WS9 | WS10 | WS11 | WS12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| W1 | • | • | • | • | • | • | • | • | • | • | • | • |
| W2 | • | • | • | • | • | • | • | • | • | • | • | • |
| W3 | • | • | • | • | • | • | • | • | • | • | • | • |
| W4 | • | • | • | • | • | • | • | • | • | |||
| W5 | • | • | • | • | • | • | • | • | • | • | • | • |
| W6 | • | • | • | • | • | • | • | • | • | • | • | |
| W7 | • | • | • | • | • | • | • | • | • | • | • | • |
| W8 | • | • | • | • | • | • | • | • | ||||
| W9 | • | • | • | • | • | • | • | • | • | • | • | • |
| W10 | • | • | • | • | • | • | • | • | • | • | ||
| W11 | • | • | • | • | • | • | • | • | • | • | • | • |
| W12 | • | • | • | • | • | • | • | • | • | • | • | • |
Abbreviations: W – Worker; WS - Workstation.
4.2. Convergence of the algorithm
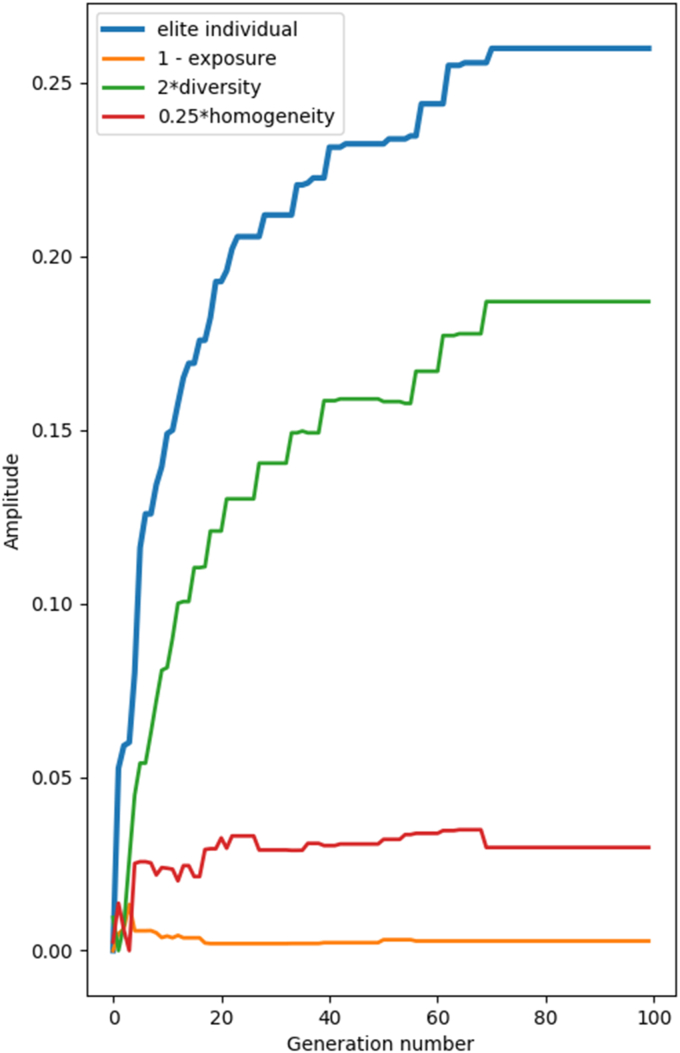
The fitness function guides the algorithm during the iterative process and it is expected to improve all variables contributing to the quality score. Therefore, the occupational exposure score should decrease, and diversity and homogeneity scores should increase. Figure 7 shows a higher improvement for diversity and homogeneity as expected, but on the other hand, exposure did not change significantly during the entire process. Regarding the quality score, the best job rotation plan in the population over the iteration process was verified as an improvement.
Figure 7.
Convergence of the algorithm considering exposure (orange), diversity (green), and homogeneity (red).
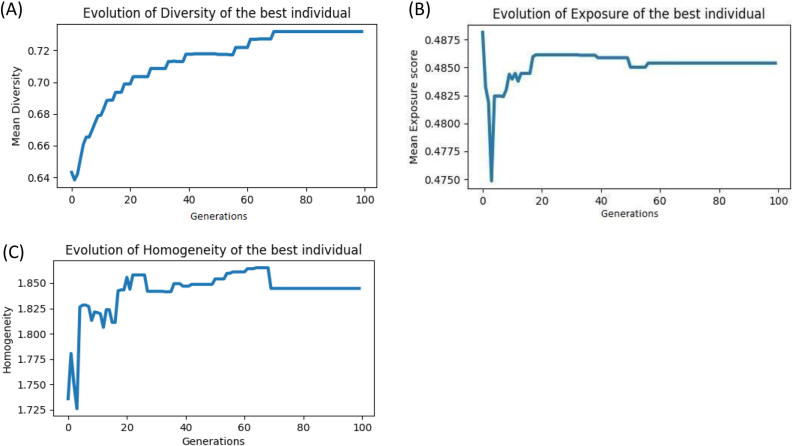
Figure 8 gives the evolution of the execution of the algorithm concerning exposure, diversity, and homogeneity and reflects the capacity of the algorithm to progressively generate better solutions by employing simulated evolution techniques.
Figure 8.
Evolution of the fitness of the best individual throughout the generations, concerning diversity (A), exposure (B), and homogeneity (C).
The algorithm reaches a stable solution around the 70th iteration.
4.3. Job rotation schedule obtained
The algorithm took 53 s to generate the proposition of a job rotation plan for the problem proposed: 12 workers, 12 workstations, and 4 working periods. The working computer used an Intel i5 quad core processor with 3.2 GHz, 8 GB of RAM and ran on a Linux Ubuntu 18.0.1 operative system.
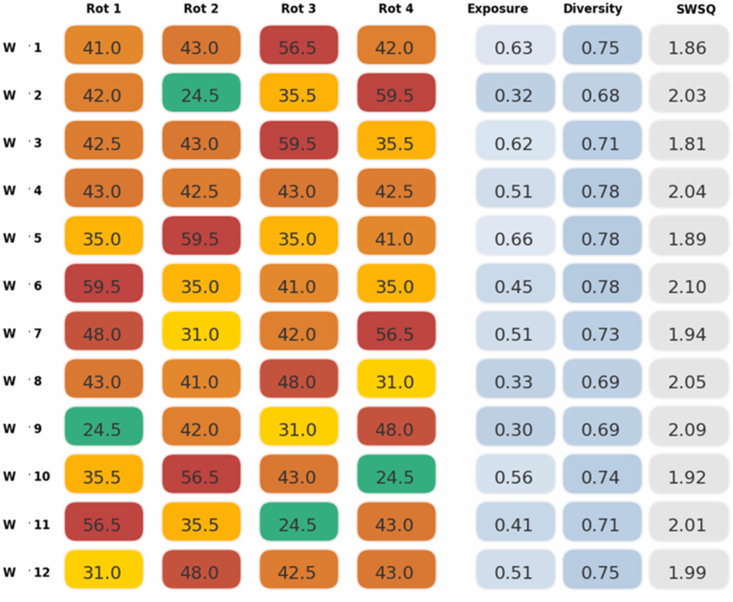
The best solution obtained is presented in Figure 9. In this solution, the allocation of workers to workstations satisfied the restrictions imposed on the problem and tried to decrease the prolonged time consumed by the same movement. During the working day, the workers were not assigned to the same workstations and did not occupy two red workstations. This happened mainly because diversity was highly promoted over the iteration process, resulting in working sequences with better diversity results. In the last 3 columns of Figure 9, the contribution of each worker to the fitness function is given with the values of exposure, diversity, and SWSQ.
Figure 9.
Best scored job rotation schedule for the last iteration of the algorithm. Each cell is coloured considering the colour traffic light scheme used to classify the risk of the workstation. Scores: 1.98,. Abbreviations: W – Worker; Rot – Rotation period; SWSQ - Shift working sequence quality.
The scores for the job rotation schedules obtained are presented in Table 5. As expected, the first matrix had the worst score compared to the last matrix (2.02 and 2.44, respectively). This was due to the fact that the first matrix had the worst set of occupational exposure and diversity scores, and these scores were not homogenous. The final score had a better homogeneity score when compared to the initial score (1.84 and 1.74, respectively).
Table 5.
Results for job rotation schedules obtained in the first and last iteration.
| Best scored job rotation for 1st iteration | 1.80 | 1.74 | 2.23 |
| Worst scored job rotation for 1st iteration | 1.63 | 1.59 | 2.02 |
| Best scored job rotation for the last iteration | 1.98 | 1.84 | 2.44 |
Abbreviations: - Mean shift working sequence quality; – Homogeneity; – Matrix quality.
An improvement in the results during the iteration process resulted in a better solution, i.e., in a better job rotation schedule for this specific team.
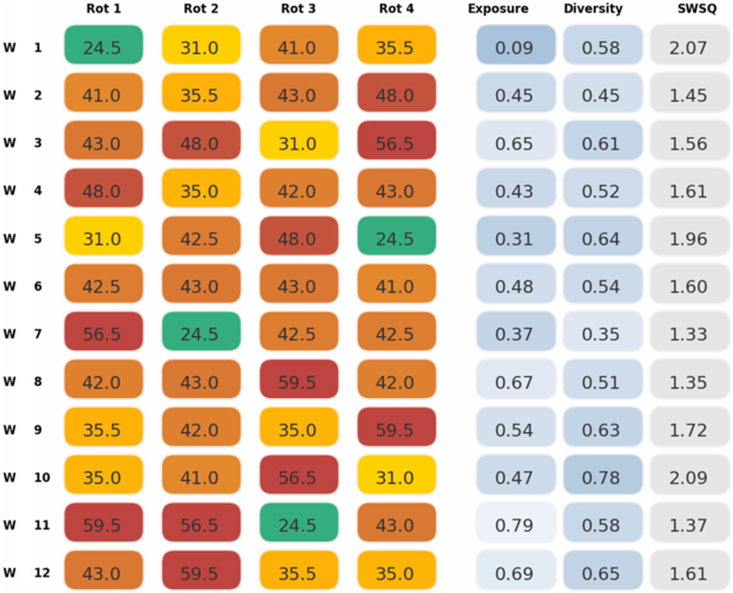
A job rotation plan designed by a team leader is presented in Figure 10.
Figure 10.
Example of a job rotation plan designed by a team leader. Abbreviations: W – worker; Rot – Rotation; – Shift working sequence quality.
For evaluation purposes, look at , , and . Besides the risk level of the workstations, scores for the sequence evaluation are presented, namely the exposure, the diversity, and the sequence quality score. The sequence of workstations attributed to was medium levelled, except for the first workstation, which had a low-risk level. This fact was verified by the exposure score, which was 0.09, close to 0, reflecting that this sequence was near to the best possible sequence could have. Nevertheless, the diversity score of was not as good (0.58). This shows how different the evaluation made for the diversity was between the three workers. Regarding , the scores were different. In this case, the sequence had two red-labelled workstations, which increased the exposure score. On the other hand, the diversity score was the same as for . This demonstrates how different the measures of exposure and diversity were. A sequence of workstations with low-levelled scores might be good in terms of exposure, but might be bad in diversity, because it measures different outcomes. For instance, had the worst diversity score of the team. This was a result of the two identical workstations at the end of the shift, therefore compromising the diversity score at the last transition.
When comparing the best results obtained by the GA for one day (Table 5), with a full week planned by the team leader (Table 6), we found that the algorithm provided better results in all the parameters, including homogeneity, diversity, and matrix quality, regardless of the day analysed.
Table 6.
Scores for shift working sequence quality, homogeneity, and matrix quality for job rotation schedules for a week designed by a team leader. These schedules were scored with the formulation designed.
| Team Leader Matrix | |||
|---|---|---|---|
| Day 1 | 1.72 | 1.77 | 2.16 |
| Day 2 | 1.64 | 1.71 | 2.07 |
| Day 3 | 1.72 | 1.73 | 2.15 |
| Day 4 | 1.76 | 1.74 | 2.20 |
| Day 5 | 1.69 | 1.70 | 2.12 |
Abbreviations: – Shift working sequence quality; – homogeneity; – Matrix quality.
5. Discussion
The main purposes of this study were: (1) to develop a formulation based on objective ergonomic indicators and workers qualifications to generate job rotation schedules based on three main criteria: diversity, exposure and homogeneity for an assembly line of the automotive industry solved by means of a GA; and (2) provide an industrial case study where the GA was tested and applied to a randomly selected team from the automotive assembly area in a real life-environment, in order to compare the performance of the job rotation plan formulated by the new GA versus that of the team leader. The algorithm proposed showed a high diversity sequence during working hours, a lower overall exposure, and reassured homogeneity to balance the rotation within each team. These results also demonstrate that the time spent by the team leader organizing the weekly schedule was considerably higher when compared with the time that the algorithm took to deliver a job rotation plan for a week.
A job rotation plan is an essential tool to the automotive industry and its aim is to facilitate not only the work of the team leader but also, in the long run, to reduce the risk associated with musculoskeletal injuries by increasing diversity, decreasing exposure, and ensuring homogeneity. This investigation, through its resources and departments, namely the industrial engineering, the ergonomics, and the occupational health teams, built a job rotation plan using a GA. The algorithm had a good computational performance and generated a solution that took less time building a rotation plan, when compared with that of the team leaders. More specifically, it took the algorithm 53 s to generate a job rotation plan, where usually team leaders spend approximately 2–3 h. Thus, the use of GA has the potential to spare the team leaders time for allocation to other important tasks. The reduction in the time to generate a job rotation plan is in accordance with other studies that also used this type of algorithms (Asensio-Cuesta et al., 2012a; Diego-Mas, 2020; Diego-Mas et al., 2009; Hochdörffer et al., 2018a).
Our results also suggest that the repetition of the same workstation, followed by rotation periods, although allowed, was not promoted by the method. This is a result of the algorithm giving higher relevance to the diversity score. This score has a wide progression and is the major factor of convergence. It also demonstrates that the algorithm can improve the conditions from the first iteration to the last and give a result that reflects the need for increased diversity and homogeneity, and decreased exposure. Diego et al. applied a GA in an automotive parts supplier assembly plant considering the previous rotations, trying to minimize the performance with the same body region, but not quantifying it, as we did with diversity (Diego-Mas et al., 2009). The option to favour diversity was supported by the physiologic pathways of musculoskeletal health stating that posture and load variation are beneficial (Mathiassen, 2006). One of the strengths and a novelty of this study is the fact that it included the calculation of diversity of force and MMH along with posture, which provides more risk factors being embedded by the GA, whereas, the majority of the algorithms presented in the literature relied on posture and movement, ergonomic score (from an evaluation method, e.g. OCRA, EAWS), learning skills, and others (Padula et al., 2017).
As far as exposure is concerned, it is one of the parameters contributing to the fitness function, but with less weight than diversity. In the literature, the cumulative exposure, with different criteria's used between studies, is one of the key factors to evaluate the effectiveness of the job rotation schedule (Asensio-Cuesta et al., 2012a; Diego-Mas et al., 2009; Hochdörffer et al., 2018b; Rajabalipour Cheshmehgaz et al., 2012; Xu et al., 2012). In this study, exposure did not change significantly because its weight was very low when compared to diversity. The choice to promote diversity over occupational exposure reflects the idea to promote an opportunity of relaxing overloaded motor units by having workstations that differ in all the risk factors considered (Mathiassen, 2006). Besides, the proposed formulation also considered homogeneity as a key feature, allowing workers to have a similar exposure during the shift. The team selected showed characteristics of versatility that were reflected on the matrix of the work team, where most of the workers were able to perform the majority of the workstations with autonomy. This is beneficial for workers since they have the possibility to improve their diversity and reduce exposure during the shift. A previous study has considered the balance between the workers as a contribution to the target function (Diego-Mas et al., 2009).
Even though there is no consensus in the literature about the effectiveness of this measure in the prevention of WRMSD's (Comper and Padula, 2014), several approaches have been implemented, considering different criteria (Padula et al., 2017). The use of GA to generate job rotation plans in the industry is a common option due to its combinatorial nature and satisfactory results (Asensio-Cuesta et al., 2012a; Diego-Mas et al., 2009). The decision to use a GA to solve the combinatorial problem in designing the job rotation plan in this study was due to it already being proven to be successfully used similar context (Asensio-Cuesta et al., 2012a; Diego-Mas et al., 2009). The methods that were applied for selection, crossover, and mutation are well known and were used because these were found to be adequate for this problem (Moscato, 1989). The mutation rate, in this case, was higher than what is usually found in the literature, but better convergence results were reached with a higher mutation rate. The job rotation schedules generated by the GA provided better scores than the ones developed by the team leaders in homogeneity, diversity, and matrix quality.
Any tool developed to assist in work organization must be flexible and appropriate to the specific requirements of each production process. Nevertheless, the GA can be implemented in the rest of the assembly area, due to the similarity of processes. In the future, transfers to production areas can be made with the optimization of their specificities and characteristics. It's also important to highlight that the work organization variables, such as the duration and number of working periods and the, duration, and frequency of breaks during the shift, have not been changed. However, it will be interesting to compare the results of the fitness function of the two remaining shifts, late evening, and night, since the working periods have different durations. This comparison could give different perspectives to make a more suitable duration and distribution of working periods throughout the shift at the organization level. Also, recent publications suggest that motivational and preferential aspects within the job rotation could also be integrated (Asensio-Cuesta et al., 2019).
Despite presenting a case study with 12 workers with promising results, this formulation lacks a broader application and validation in an ecological context in order, to further understand its effectiveness in a larger scale sample and musculoskeletal symptom prevention. In an era of technological development, the use of direct quantitative assessment of risk factors in the working field, such as those acquired through motion sensors, would enable the proposed formulation to have more reliable risk scores than the ones globally provided by the EAWS.
6. Conclusion
The formulation developed in this study generated job rotation schedules considering constraints present in the assembly line of the automotive industry. This formulation has been proven to be a reliable solution to design job rotation plans, increasing diversity, decreasing exposure, and balancing homogeneity for the team. The solution presented in this study combined the information from workers in terms of qualification and the requirements of the workstations to generate and evaluate solutions looking for the best sequences. Moreover, this approach helped the team leaders, in a time-efficient manner, to decide which job rotation plan would be better suited when considering all the constraints, his experience and his knowledge about the workstations and his team.
From the company point of view, this approach could additionally be a relevant tool for data generation, which could be crucial for designing new production systems and to manage investments aimed at improving productivity and promote musculoskeletal health at work. Nonetheless, future research is warranted to analyse the effectiveness of the job rotation plans generated by this type of formulations with those provided by the team leaders, while considering a larger sample, how the plans impact the results of diversity, exposure, and homogeneity, and how they translate into the reduction of the prevalence of WRMSD.
Declarations
Author contribution statement
Ana Assunção and João Rodrigues: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper.
Nafiseh Mollaei and Carlos Fujão: Conceived and designed the experiments; Analyzed and interpreted the data; the paper.
Daniel Osório: Contributed reagents, materials, analysis tools or data.
António P. Veloso: Analyzed and interpreted the data.
Hugo Gamboa: Performed the experiments; Analyzed and interpreted the data.
Filomena Carnide: Conceived and designed the experiments; Analyzed and interpreted the data; Wrote the paper.
Funding statement
Ana Assunção was supported by Fundação para a Ciência e Tecnologia [SFRH/BDE/102750/2014].
Nafiseh Mollaei was supported by Fundação para a Ciência e Tecnologia [PD/BDE/142973/2018].
João Rodrigues was supported by Fundação para a Ciência e Tecnologia [PD/BDE/142816/2018].
This work was partly supported by Fundação para a Ciência e Tecnologia (CIPER - Centro Interdisciplinar para o Estudo da Performance Humana (Unit 447) [UIDB/00447/2020].
Data availability statement
Data will be made available on request.
Declaration of interests statement
The authors declare no competing interests.
Additional information
No additional information is available for this paper.
Acknowledgements
The authors are grateful to all participants for their time and effort.
Appendix A. Supplementary data
The following is the supplementary data related to this article:
References
- Aryanezhad M.B., Kheirkhah A.S., Deljoo V., Mirzapour Al-E-Hashem S.M.J. Designing safe job rotation schedules based upon workers’ skills. Int. J. Adv. Manuf. Technol. 2009 [Google Scholar]
- Asensio-Cuesta S., Diego-Mas J.A., Canós-Darós L., Andrés-Romano C. A genetic algorithm for the design of job rotation schedules considering ergonomic and competence criteria. Int. J. Adv. Manuf. Technol. 2012 [Google Scholar]
- Asensio-Cuesta S., Diego-Mas J.A., Cremades-Oliver L.V., González-Cruz M.C. A method to design job rotation schedules to prevent work-related musculoskeletal disorders in repetitive work. Int. J. Prod. Res. 2012;50:7467–7478. [Google Scholar]
- Asensio-Cuesta S., García-Gómez J.M., Poza-Luján J.L., Conejero J.A. A game-theory method to design job rotation schedules to prevent musculoskeletal disorders based on workers’ preferences and competencies. Int. J. Environ. Res. Publ. Health. 2019;16:4666. doi: 10.3390/ijerph16234666. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bao S. Handbook of Clinical Neurology. Elsevier B.V.; 2015. Mechanical stress; pp. 367–396. [Google Scholar]
- Bhasin H., Behal G., Aggarwal N., Saini R.K., Choudhary S. On the applicability of diploid genetic algorithms in dynamic environments. Soft Comput. 2016;20:3403–3410. [Google Scholar]
- Boenzi F., Digiesi S., Mossa G., Mummolo G., Romano V.A. Optimal break and job rotation schedules of high repetitive – low load manual tasks in assembly lines: an OCRA – based approach. IFAC Proc. 2013;46:1896–1901. [Google Scholar]
- Carnahan B.J., Redfern M.S., Norman B. Designing safe job rotation schedules using optimization and heuristic search. Ergonomics. 2000;43:543–560. doi: 10.1080/001401300184404. [DOI] [PubMed] [Google Scholar]
- Comper M.L.C., Padula R.S. The effectiveness of job rotation to prevent work-related musculoskeletal disorders: protocol of a cluster randomized clinical trial. BMC Muscoskel. Disord. 2014 doi: 10.1186/1471-2474-15-170. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Kok J., Vroonhof P., Snijders J., Roullis G., Clarke M., Peereboom K., Dorst P. van., Isusi I. European Agency for Safety and Health at Work; 2019. Work-related Musculoskeletal Disorders : Prevalence, Costs and Demographics in the EU. [Google Scholar]
- Diego-Mas J.A. Designing cyclic job rotations to reduce the exposure to ergonomics risk factors. Int. J. Environ. Res. Publ. Health. 2020;17:1073. doi: 10.3390/ijerph17031073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Diego-Mas J.A., Asensio-Cuesta S., Sanchez-Romero M.A., Artacho-Ramirez M.A. A multi-criteria genetic algorithm for the generation of job rotation schedules. Int. J. Ind. Ergon. 2009;39:23–33. [Google Scholar]
- Digiesi S., Facchini F., Mossa G., Mummolo G. Minimizing and balancing ergonomic risk of workers of an assembly line by job rotation: a MINLP Model. Int. J. Ind. Eng. Manag. 2018;9:129–138. [Google Scholar]
- Durand M.J., Corbière M., Coutu M.F., Reinharz D., Albert V. Work; 2014. A Review of Best Work-Absence Management and Return-To-Work Practices for Workers with Musculoskeletal or Common Mental Disorders. [DOI] [PubMed] [Google Scholar]
- Goldberg D.E. first ed. Addison-Wesley Longman Publishing Co., Inc.; USA: 1989. Genetic Algorithms in Search, Optimization and Machine Learning. [Google Scholar]
- Hochdörffer J., Hedler M., Lanza G. Staff scheduling in job rotation environments considering ergonomic aspects and preservation of qualifications. J. Manuf. Syst. 2018 [Google Scholar]
- Hochdörffer J., Hedler M., Lanza G. Staff scheduling in job rotation environments considering ergonomic aspects and preservation of qualifications. J. Manuf. Syst. 2018;46:103–114. [Google Scholar]
- Jorgensen M., Davis K., Kotowski S., Aedla P., Dunning K. Characteristics of job rotation in the Midwest US manufacturing sector. Ergonomics. 2005;48:1721–1733. doi: 10.1080/00140130500247545. [DOI] [PubMed] [Google Scholar]
- Mathiassen S.E. Diversity and variation in biomechanical exposure: what is it, and why would we like to know? Appl. Ergon. 2006;37:419–427. doi: 10.1016/j.apergo.2006.04.006. [DOI] [PubMed] [Google Scholar]
- McDonald T., Ellis K.P., Van Aken E.M., Patrick Koelling C. Development and application of a worker assignment model to evaluate a lean manufacturing cell. Int. J. Prod. Res. 2009;47:2427–2447. [Google Scholar]
- Moscato P. On genetic crossover operators for relative order preservation. C3P Rep. 1989 [Google Scholar]
- Mossa G., Boenzi F., Digiesi S., Mummolo G., Romano V.A. Productivity and ergonomic risk in human based production systems: a job-rotation scheduling model. Int. J. Prod. Econ. 2016 [Google Scholar]
- Padula R.S., Comper M.L.C., Sparer E.H., Dennerlein J.T. Job rotation designed to prevent musculoskeletal disorders and control risk in manufacturing industries: a systematic review. Appl. Ergon. 2017 doi: 10.1016/j.apergo.2016.07.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rajabalipour Cheshmehgaz H., Haron H., Kazemipour F., Desa M.I. Accumulated risk of body postures in assembly line balancing problem and modeling through a multi-criteria fuzzy-genetic algorithm. Comput. Ind. Eng. 2012;63:503–512. [Google Scholar]
- Rodriguez A.C., Barrero L.H. Job rotation: effects on muscular activity variability. Appl. Ergon. 2017;60:83–92. doi: 10.1016/j.apergo.2016.11.005. [DOI] [PubMed] [Google Scholar]
- Schaub K., Caragnano G., Britzke B., Bruder R. The European assembly Worksheet. Theor. Issues Ergon. Sci. 2013;14:616–639. [Google Scholar]
- Sebbag E., Felten R., Sagez F., Sibilia J., Devilliers H., Arnaud L. The world-wide burden of musculoskeletal diseases: a systematic analysis of the World Health Organization Burden of Diseases Database. Ann. Rheum. Dis. 2019 doi: 10.1136/annrheumdis-2019-215142. annrheumdis-2019. [DOI] [PubMed] [Google Scholar]
- Xu Z., Ko J., Cochran D.J., Jung M.C. Design of assembly lines with the concurrent consideration of productivity and upper extremity musculoskeletal disorders using linear models. Comput. Ind. Eng. 2012 [Google Scholar]
- Yung M., Mathiassen S.E., Wells R.P. Variation of force amplitude and its effects on local fatigue. Eur. J. Appl. Physiol. 2012 doi: 10.1007/s00421-012-2375-z. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Data will be made available on request.