Summary.
Truncated survival data arise when the event time is observed only if it falls within a subject specific region. The conventional risk-set adjusted Kaplan–Meier estimator or Cox model can be used for estimation of the event time distribution or regression coefficient. However, the validity of these approaches relies on the assumption of quasi-independence between truncation and event times. One model that can be used for the estimation of the survival function under dependent truncation is a structural transformation model that relates a latent, quasi-independent truncation time to the observed dependent truncation time and the event time. The transformation model approach is appealing for its simple interpretation, computational simplicity and flexibility. In this paper, we extend the transformation model approach to the regression setting. We propose three methods based on this model, in addition to a piecewise transformation model that adds greater flexibility. We investigate the performance of the proposed models through simulation studies and apply them to a study on cognitive decline in Alzheimer’s disease from the National Alzheimer’s Coordinating Center. We have developed an R package, tranSurv, for implementation of our method.
Keywords: Alzheimer’s disease, Cox model, Inverse probability weighting, Kendall’s tau, Quasi-independence
1. Introduction
Truncated time to event data arise in various fields of study, including biomedical sciences, public health, epidemiology, and astronomy. It is a type of biased sampling, in which the event time is observed only if it falls within a certain interval. In a study of the National Alzheimer’s Coordinating Center (NACC), the primary goal was to assess the association between Apolipoprotein E (APOE) genotype, gender, and other features and the time from onset of cognitive decline to death. The time from onset of cognitive decline to death is left-truncated by the time from cognitive decline to NACC entry for the participants who experienced cognitive impairment prior to their NACC study entry. Since some subjects drop out during follow-up or are alive at the end of follow-up, the event time is also right-censored. Figure 1 illustrates these left-truncated and right-censored data. As another example, in an autopsy substudy of the NACC cohort, because a subject’s time of death has to be earlier than the time of data extraction, the time from NACC entry to death is right-truncated by the time from the NACC entry to data extraction. In the absence of censoring, right truncation turns into left truncation by reversing the time scale (Lagakos et al., 1988), such as our second NACC data example. In the presence of left truncation, most conventional methods used in survival analysis such as the Kaplan–Meier estimator, the Nelson–Aalen estimator and the proportional hazards model can be applied after adjustment of the risk sets. This approach requires quasi-independence (Tsai, 1990), i.e., independence between truncation and event times in the observable region. Recently, the validity of the risk-set based estimators was shown to depend on a weaker condition termed the factorization assumption (Vakulenko-Lagun et al., 2019). The risk-set based methods can lead to biased estimation and incorrect interpretation when these assumptions are not met.
Fig. 1.
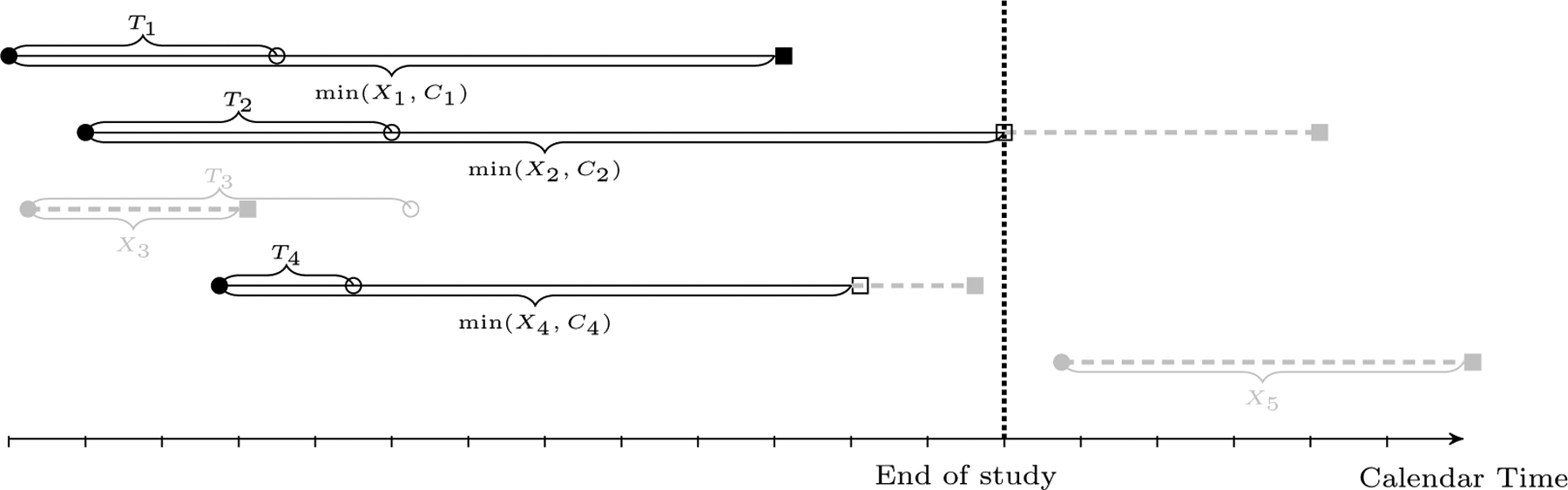
Illustration of left-truncated and right-censored data; X: event time of interest, T: left truncation time, C: right censoring time; black circle: initial time, white circle: calendar time of enrollment to the study, black square: calendar time of the occurring of event of interest. The gray segments are time intervals that are not observed. The event time of subject 3 is left truncated and unobservable since the event of interest happens before study enrollment. The event times of subjects 1, 2, and 4 are left truncated since the event of interest has not happened by the time of study enrollment. The event times of subjects 2 and 4 are right-censored. The event time of subject 5 is left truncated since the initial time of the event is later than the end of study.
Quasi-independence can be tested using the observed data (Vakulenko-Lagun et al., 2019). Standard tests that are powerful for detecting monotone dependence include the conditional Kendall’s tau test (Tsai, 1990) and the conditional Pearson’s product-moment correlation coefficient test (Chen et al., 1996). The conditional Kendall’s tau test has received more attention in the literature due to its simplicity and accessibility in the presence of right censoring. Modifications of conditional Kendall’s tau tests have been proposed to accommodate complicated truncation schemes (Martin and Betensky, 2005), improve power (Emura and Wang, 2010) and eliminate bias (Austin and Betensky, 2014). To accommodate non-monotone alternatives, Rodríguez-Girondo and de Uña-Álvarez (2012), de Uña-Álvarez (2012) and Rodríguez-Girondo and de Uña-Álvarez (2016) proposed bootstrap-based global and local conditional Kendall’s tau tests. Chiou et al. (2018) proposed flexible permutation tests that are powerful for general dependence structures. If the null of quasi-independence is rejected by these tests, or if the subject matter suggests dependent truncation, modifications must be made to incorporate the dependence.
When the event time distribution is of interest, a convenient approach is to apply a copula-based model in which the association structure between the truncation and event time is specified parametrically, while leaving the marginal distributions unspecified (Lakhal-Chaieb et al., 2006; Emura et al., 2011; Emura and Wang, 2012; Emura and Murotani, 2015). Some guidelines for selecting an appropriate copula are provided in Beaudoin and Lakhal-Chaieb (2008). Correct specification of the copula is critical, as the performance of the approach relies upon it. As an alternative to the copula-based approach that avoids its strong modeling assumptions, Efron and Petrosian (1994) proposed a transformation model for estimation of a latent quasi-independent truncation variable that can be used in simple risk-set adjusted estimation in the absence of censoring. The transformation model approach was extended to accommodate right censoring through restriction to the uncensored event times along with inverse probability weighting of the censoring distribution (Chiou et al., 2019). More recently, Vakulenko-Lagun et al. (in press) proposed inverse probability weighting methods to estimate the event time distribution when shared covariates induce the dependence between the truncation and event times.
When covariate effects are of interest, the Cox model is often used. All that is required is conditional independence between the truncation and event times conditional on covariates. In this paper we consider settings in which conditional independence does not hold. The literature on regression models under dependent truncation is sparse. Jones and Crowley (1992) accounted for dependent truncation by including the truncation time as an additional covariate in proportional hazards models. As a useful alternative, Emura and Wang (2016) proposed a semiparametric accelerated failure time model that is similar in flavor to that of Jones and Crowley (1992) in including the truncation time as an additional regressor. These approaches make strong assumptions on the nature of the dependence. Emura and Wang (2016) imposed an alternative requirement of quasi-independence between the residual lifetime and the residual truncation time, and derived rank-based estimating equations.
In this paper, we extend the transformation model of Efron and Petrosian (1994) and Chiou et al. (2019) to the regression setting in which conditional independence between truncation and event times given covariates does not hold. In the absence of censoring, we assume there exists a latent quasi-independent truncation time that is associated with the observed dependent truncation time and the observed event time through an unknown transformation parameter. The transformation model ensures that the truncation ordering is preserved. When the dependence between the truncation and event times is not induced by a covariate, the transformation parameter is chosen to minimize that dependence, as measured by conditional Kendall’s tau (Martin and Betensky, 2005). When the dependence between the truncation and event times is additionally induced by covariates, the transformation parameter is chosen to minimize the magnitude of the regression coefficients of functions of the truncation time. When censoring is present, we restrict the analysis to the uncensored observations and adjust for this biased selection via inverse probability weighting using the censoring distribution. We also propose goodness-of-fit diagnostic procedures similar to those in Chiou et al. (2019) to assess the adequacy of the transformation model. We have developed an R package, tranSurv (Chiou and Qian, 2021) for implementation of our methods.
In Section 2, we propose transformation approaches for uncensored data and develop goodness-of-fit assessments. Extensions to censored data and the requisite inverse weighting adjustment are described in Section 3. We investigate the finite sample performance of the proposed procedures through simulation studies in Section 4. The method is applied to datasets from Alzheimer’s disease studies in Section 5. We conclude with a discussion in Section 6.
2. Transformation approach for uncensored data
We first consider regression analysis for time-to-event data in the absence of censoring. Let X denote the event time and T denote the left truncation time; X and T may be dependent and X is observed only if T ≤ X. If the event time X* is right truncated by T* as it is in the NACC autopsy data example described in Section 1, i.e., X* is observable only if X* ≤ T*, we can turn right truncation into left truncation by reversing the time scale (Lagakos et al., 1988). Essentially, we let X = τt − X* and T = τt − T*, where τt is a pre-specified constant such as the maximum value of T* in the observable region. Then X* ≤ T* is equivalent to T ≤ X, and thus X is left-truncated by T. Let Z denote a p × 1 covariate vector. The observed data then consist of n independent and identically distributed copies of {T, X, Z|X ≥ T}, i.e., {(ti, xi, zi|xi ≥ ti), i = 1,…, n}. We assume the Cox proportional hazards model for X given Z:
| (1) |
where λ0(·) is the unspecified baseline hazard function and β is a p × 1 vector of regression coefficients. Under the quasi-independence assumption (Tsai, 1990) between the left truncation time T and event time X, a standard method to obtain the coefficient estimator, , is to maximize the partial likelihood (Cox, 1975), with risk sets adjusted for left truncation:
The quasi-independence assumption is testable using conditional Kendall’s tau (Tsai, 1990; Martin and Betensky, 2005). When quasi-independence does not hold, alternative estimation procedures are required for estimating the regression coefficients under (1).
For estimation of the marginal distribution of X in the absence of covariates, Efron and Petrosian (1994) suggested a transformation approach to deal with the dependence between T and X. The transformation approach assumes that there exists a latent, quasi-independent left truncation time T′(a) for X in the absence of the dependence:
| (2) |
where a is an unknown transformation parameter. This transformation model preserves the truncation ordering X > T as long as a > −1, though the between-subjects ordering of the truncation times may be different after the transformation. We assume the transformation model only over the observable region X > T, as required by the definition of quasi-independence, which defines the transformation parameter.
The linear transformation model (2) may not hold on the whole support of X, but rather may hold within the segments of the support of X. Defining a sequence 0 = b0 < b1 < … < bK = sup(X) that divides the support of X into K segments, we consider a robust, piecewise linear transformation model with K transformation parameters ak, k = 1, …, K, each of which is used to compute the latent independent truncation time corresponding to one of the K segments, i.e.,
| (3) |
where I(A) = 1 if the event A occurs and 0 otherwise. The number of segments K for the robust, piecewise linear transformation model (3) can be determined by the goodness of fit procedure proposed in Chiou et al. (2019), which we describe in detail in Section 2.3. In practice, we would like to keep the number of segments K as small as possible. We start with one breakpoint, and move up to two breakpoints if the goodness of fit hypothesis test rejects the one breakpoint, and so on. The breakpoints bk’s are chosen to divide the event times into K equally populated segments. We also recommend a scatter plot of X − T versus X to visualize the potential nonlinearity, as an aide for an alternative selection of breakpoints.
In the absence of covariates, a (or ak) can be estimated by inverting tests of quasi-independence of T′(a) (or T′(ak)) and X (Chiou et al., 2019). However, it is not obvious how to estimate a in the presence of covariates, since either the truncation time, event time or both may depend on the covariates. In the following, we propose two approaches for estimation of the transformation parameter a and the regression coefficient β. The first employs an unadjusted transformation via a conditional Kendall’s tau, which assumes that Z is unrelated to the transformation parameter a. The second employs an adjusted transformation via a Cox model, which allows Z to impact the transformation parameter a.
2.1. Unadjusted transformation via conditional Kendall’s tau
Motivated by Efron and Petrosian (1994), we consider an estimation procedure that requires quasi-independence between T′(a) and X, without conditioning on Z. The conditional Kendall’s tau, denoted as τc, is commonly used to test the quasi-independence assumption due to its simplicity and rank invariance property. Given random vectors and , the conditional Kendall’s tau is defined as , where sgn(u) = I(u > 0) − I(u < 0), I(·) is the indicator function, and is the event of comparable pairs. In the absence of censoring, Martin and Betensky (2005) proposed a consistent, U-statistic estimator of τc(a),
where . We propose to estimate the transformation parameter, a, as the solution to , and if this is not attainable, we take it to be the minimizer of . Once a is estimated, the standard Cox proportional hazard model that requires quasi-independence can be applied to , in place of {T, X}, to estimate β. Specifically, we obtain by maximizing the modified partial likelihood
We use the simple nonparametric bootstrap approach to estimate the variance of . We refer to this approach based on the conditional Kendall’s tau as the CK approach.
2.2. Adjusted transformation via Cox model
Our second approach exploits the fact that for use of the Cox model, we require the weaker assumption of quasi-independence between T′(a) and X conditional on Z. We propose an estimation procedure that inverts the test for conditional quasi-independence proposed by Jones and Crowley (1992). Specifically, we consider a Cox model for X that adjusts for left-truncation by T′(a), and includes Z and T′(a) as covariates. Following the arguments in Jones and Crowley (1992), for a fixed a, the estimated regression coefficient T′(a) can be used to test for conditional quasi-independence between T′(a) and X given Z, while adjusting for left truncation of X by T′(a). Thus, we propose to estimate a as the value that minimizes the absolute value of the regression coefficient for T′(a). We refer to this covariate-adjusted approach as the Cox1 approach.
This approach is well-suited to a monotone dependence relationship between X and T. To accommodate non-monotone dependence structures, we consider including non-linear functions of T′(a) as covariates. Defining W{T′(a)} as a q × 1 covariate vector constructed from T′(a), we estimate a as the value that yields the minimum , where
| (4) |
α is a q × 1 vector of regression coefficients and ‖ · ‖ is the l2 norm of a vector. Given a, the observed data are {ti(a), xi, wi(a), zi|xi ≥ ti}, i = 1, …, n, where . We estimate a by maximizing the partial likelihood
with respect to α and β for each a and selecting the value of a associated with the minimum . We take the associated as the estimate for β. We refer to this covariate-adjusted approach as the Cox2 approach.
The Cox2 approach offers flexibility as the covariate functions, W{T′(a)}, may be selected to accommodate any plausible hazard function association structure between X and T. For example, W{T′(a)} = [T′(a), {T′(a)}2]⊤ accommodates a quadratic association. Discretization of T′(a) can be implemented to accommodate skewness in T′(a) and offers a more robust modeling approach. For example, W{T′(a)} could be indicator variables that indicate whether T′(a) falls into different percentile based intervals. In the following, we consider , where and indicate the first and second tertiles of T′(a).
2.3. Goodness of fit assessments for the linear transformation model
We propose a two-step goodness-of-fit procedure. We first implement the procedure proposed in Chiou et al. (2019). Under the transformation model, it follows that , which still holds for truncated data X ≥ T. Thus, we assess the model by regressing (X − T) on a piecewise linear function of X. If the linear transformation model in (2) holds, the piecewise model will not be favored over the linear model. If the piecewise linear model is favored, we proceed to fit separate transformation models for the corresponding pieces as proposed in (3). Estimates of the coefficients can be obtained nonparametrically by adjusting for left truncation of X − T by zero and under the assumption of a symmetric error distribution (e.g., Tsui et al., 1988; Karlsson, 2006). We demonstrate the goodness-of-fit procedure in Section 5.
If the goodness-of-fit assessment in the first step does not reject the linear transformation model, we proceed with a second assessment. To test the adequacy of a particular method, we include the estimated T′(a) from that particular method as a covariate in the form, , in addition to other covariates, in (4), with adjustment for left truncation by T′(a). If the ℓ2 norm of the coefficient α in equation (4) is not small or the p-value for the regression coefficient W{T′(a)} is small, we conclude that residual dependence between the event time and transformed truncation time may persist even after the transformation. We can address this by including W{T′(a)} as a covariate in the model to accommodate the residual dependence, in the spirit of the Jones and Crowley approach that adjusts for T, and interpret the results accordingly.
3. Transformation approach for censored data
In the presence of right censoring, the event time X is not fully observed, and the transformation approach in Section 2 cannot be applied directly. Let C denote the censoring time measured from the same time origin as X. We assume that censoring may happen before the truncation, i.e., Pr(T ≤ C) < 1. Subjects are sampled only if Y ≥ T, where Y = min(X, C) is the observed event time. Conditional on Z, we assume that C is independent of (X, T). Other censoring models exist, and we refer to Qian and Betensky (2014) for a detailed discussion. Let Δ = I(X ≤ C) be the event indicator. Under left truncation and right censoring, the observed data consist of n independent and identically distributed copies of {Y, T, Δ, Z|Y ≥ T}, i.e., {(yi, ti, δi, zi|yi ≥ ti), i = 1, …, n}. Since the transformation model specifies the dependence structure between T and X, and not T and Y, it is not possible to apply the transformation model to (T, Y). Instead, we apply the model to the uncensored data and adjust for the accompanying selection bias using inverse probability of censoring weighting in the estimation.
3.1. Unadjusted transformation via conditional Kendall’s tau
We extend the estimating procedure in Section 2.1 to censored data by inverting a weighted version of conditional Kendall’s tau test, which adjusts for the selection of uncensored observations by inverse probability weighting of censoring. This version of Kendall’s tau was proposed by Austin and Betensky (2014) and has the form , where
, and is the Kaplan–Meier estimator for SC(u) = Pr(C > u). Under the assumption that C is independent of (X, T), can be obtained by adjusting for quasi-independent left truncation and independent right censoring. The estimator of the transformation parameter a is the minimizer of .
Upon successful estimation of a, we continue to use the properly weighted uncensored observations, along with the corresponding latent independent truncation times, to estimate β. Under the Cox proportional hazards model, the weighted partial likelihood is expressed as
| (5) |
and can be obtained by maximizing it.
3.2. Adjusted transformation via Cox model
We continue to restrict to the uncensored event times when covariate-induced dependence between the truncation and event times is suspected. As in Section 3.1, we use as the sampling weight to adjust for selection bias due to restriction to the uncensored events. The modified Cox proportional hazards model in (4) leads to the weighted partial likelihood
| (6) |
As in Section 2.2, we estimate a as the value associated with the minimum . The estimate of β is the value associated with the minimum of (i.e., at the estimated a).
Even if SC(·) is not identifiable on the whole support of C and only the conditional survival function SC(t)/SC(cmin) is identifiable for t > cmin = min(y1, ⋯, yn), the estimator and the weighted partial likelihoods in equations (5) and (6) remain valid since the estimator or the likelihood expressions remain the same no matter whether SC(t) or SC(t)/SC(cmin) is used.
4. Simulation studies
4.1. Dependence not induced by covariates
We generate the covariate, Z, from a standard normal distribution. Given Z, the event times were then generated from the Cox proportional hazards model
| (7) |
with β = 1 and λ0(x) equal to a Weibull hazard function with shape 2 and scale 0.5. The latent quasi-independent truncation time T′(a) was generated from an independent gamma distribution with shape ϕ and rate 2. The dependent truncation time, T, was then constructed by inverting the linear transformation model: T = (1 + a)T′(a) − aX. We repeated this process until we obtained n = 200 or 500 observations that satisfied T ≤ Y = min(X, C), where the censoring time C was an independent exponential distribution with mean 1/r. The parameters (ϕ, a, r) were chosen to achieve a truncation proportion of 30%, two levels of post-truncation association measured by the conditional Kendall’s tau (Martin and Betensky, 2005) between (T, X)|T ≤ Y of τ = 0.2, 0.35 and four levels of censoring after truncation of 0%, 15%, 30% and 50%. We repeated each setting 1000 times. Supplementary Table S1 presents the values for (ϕ, a, r) under each scenario.
For each repetition, we applied the proposed methods from Section 3. For comparison, we fit a conventional Cox proportional hazards regression adjusting for quasi-independent left truncation (labeled “Cox QI”), as well as the same model with the truncation time T included as an additional covariate (Jones and Crowley, 1992) (labeled “JC”). Supplementary Table S2 presents the average bias for the transformation parameter estimates. The small bias indicates that our method is able to recover the latent truncation times T′(a). Table 1 summarizes the simulation results for the regression coefficient. In all scenarios, the proposed estimators are virtually unbiased, whereas the conventional Cox model and Jones and Crowley’s method display moderate to substantial bias that is related to the magnitude of the association between T and X, as measured by τ. As the censoring rate increases, the bias for these two comparison methods decreases. This is expected since right censoring dilutes the strength of dependence between truncation time and event time in the observable region (see also Chiou et al., 2019). In Table S3, where we increased the number of replications to 10,000, our proposed methods are virtually unbiased in all scenarios when the sample size n = 200. In contrast, the two comparison methods exhibit moderate to heavy bias. The empirical bias for our proposed methods generally decreases as the censoring rate increases to the 30% level. As the censoring rate increases to 50%, the empirical bias for our proposed methods increases slightly. This is because the censoring impacts our proposed methods through both the estimation of SC(·) and the estimation of transformation parameter a. As the censoring rate increases, the estimates of SC(·) and thus the inverse probability weight are improved, while the estimate of transformation parameter a that involves uncensored observations only may be less accurate.
Table 1.
Simulation results under dependence not induced by covariates†
| n = 200 | n = 500 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| cens | τ | Method | bias | ESE | ASE | CP | bias | ESE | ASE | CP |
| 0% | 0.2 | Cox QI | −0.079 | 0.104 | 0.102 | 87.0 | −0.083 | 0.061 | 0.063 | 76.2 |
| JC | −0.114 | 0.109 | 0.107 | 81.3 | −0.119 | 0.064 | 0.066 | 58.3 | ||
| CK | 0.006 | 0.106 | 0.103 | 95.7 | 0.002 | 0.062 | 0.063 | 96.0 | ||
| Cox1 | 0.004 | 0.108 | 0.105 | 95.4 | 0.001 | 0.064 | 0.065 | 95.6 | ||
| Cox2 | 0.007 | 0.109 | 0.113 | 96.3 | 0.003 | 0.064 | 0.066 | 95.6 | ||
| 0.35 | Cox QI | −0.278 | 0.097 | 0.097 | 23.3 | −0.282 | 0.057 | 0.059 | 0.7 | |
| JC | −0.427 | 0.109 | 0.108 | 4.9 | −0.434 | 0.065 | 0.066 | 0.0 | ||
| CK | 0.006 | 0.106 | 0.103 | 95.7 | 0.002 | 0.062 | 0.063 | 96.1 | ||
| Cox1 | 0.004 | 0.108 | 0.105 | 95.4 | 0.001 | 0.064 | 0.065 | 95.5 | ||
| Cox2 | 0.006 | 0.114 | 0.121 | 96.9 | 0.003 | 0.064 | 0.067 | 95.5 | ||
| 15% | 0.2 | Cox QI | −0.068 | 0.107 | 0.105 | 89.3 | −0.077 | 0.063 | 0.064 | 79.4 |
| JC | −0.101 | 0.112 | 0.110 | 84.8 | −0.111 | 0.065 | 0.067 | 64.2 | ||
| CK | 0.010 | 0.110 | 0.108 | 95.6 | 0.001 | 0.065 | 0.066 | 96.4 | ||
| Cox1 | 0.007 | 0.113 | 0.110 | 95.3 | 0.000 | 0.065 | 0.067 | 96.3 | ||
| Cox2 | 0.011 | 0.112 | 0.118 | 96.2 | 0.002 | 0.065 | 0.068 | 96.5 | ||
| 0.35 | Cox QI | −0.221 | 0.101 | 0.101 | 42.9 | −0.229 | 0.060 | 0.061 | 6.3 | |
| JC | −0.364 | 0.112 | 0.112 | 14.2 | −0.375 | 0.067 | 0.067 | 0.1 | ||
| CK | 0.007 | 0.109 | 0.107 | 96.0 | 0.000 | 0.065 | 0.065 | 96.0 | ||
| Cox1 | 0.004 | 0.111 | 0.108 | 95.6 | −0.001 | 0.067 | 0.067 | 96.1 | ||
| Cox2 | 0.009 | 0.112 | 0.120 | 96.9 | 0.001 | 0.066 | 0.067 | 96.4 | ||
| 30% | 0.2 | Cox QI | −0.060 | 0.105 | 0.107 | 91.6 | −0.061 | 0.068 | 0.067 | 82.8 |
| JC | −0.084 | 0.109 | 0.113 | 85.4 | −0.093 | 0.068 | 0.068 | 71.4 | ||
| CK | −0.002 | 0.112 | 0.114 | 95.5 | −0.001 | 0.071 | 0.071 | 95.4 | ||
| Cox1 | −0.005 | 0.114 | 0.116 | 95.4 | −0.002 | 0.071 | 0.072 | 95.3 | ||
| Cox2 | −0.003 | 0.114 | 0.117 | 95.5 | −0.001 | 0.071 | 0.072 | 96.1 | ||
| 0.35 | Cox QI | −0.188 | 0.097 | 0.109 | 56.9 | −0.188 | 0.065 | 0.068 | 20.4 | |
| JC | −0.324 | 0.113 | 0.117 | 20.2 | −0.326 | 0.070 | 0.070 | 8.0 | ||
| CK | −0.004 | 0.110 | 0.115 | 95.6 | −0.002 | 0.071 | 0.071 | 95.6 | ||
| Cox1 | −0.007 | 0.111 | 0.117 | 96.1 | −0.003 | 0.071 | 0.072 | 96.1 | ||
| Cox2 | −0.003 | 0.111 | 0.117 | 96.2 | −0.002 | 0.071 | 0.072 | 95.7 | ||
| 50% | 0.2 | Cox QI | −0.046 | 0.107 | 0.110 | 92.5 | −0.048 | 0.070 | 0.067 | 87.3 |
| JC | −0.065 | 0.109 | 0.115 | 90.2 | −0.069 | 0.072 | 0.070 | 80.3 | ||
| CK | −0.007 | 0.120 | 0.119 | 93.6 | −0.005 | 0.075 | 0.073 | 93.2 | ||
| Cox1 | −0.011 | 0.121 | 0.121 | 94.1 | −0.007 | 0.076 | 0.074 | 93.8 | ||
| Cox2 | −0.004 | 0.121 | 0.125 | 94.0 | −0.004 | 0.076 | 0.074 | 93.8 | ||
| 0.35 | Cox QI | −0.133 | 0.107 | 0.108 | 73.2 | −0.137 | 0.066 | 0.066 | 45.2 | |
| JC | −0.243 | 0.117 | 0.119 | 45.4 | −0.248 | 0.072 | 0.072 | 7.8 | ||
| CK | −0.089 | 0.117 | 0.119 | 94.9 | −0.006 | 0.074 | 0.073 | 94.0 | ||
| Cox1 | −0.013 | 0.120 | 0.121 | 94.7 | −0.008 | 0.075 | 0.074 | 94.1 | ||
| Cox2 | −0.008 | 0.118 | 0.127 | 95.4 | −0.005 | 0.074 | 0.074 | 94.2 | ||
τ, the post-truncation conditional Kendall’s tau; bias, empirical bias; ESE, empirical standard error; ASE, average of bootstrap standard error with size 500; CP, coverage (%) of 95% Wald confidence interval; JC, Jones & Crowley’s method; CK, unadjusted transformation via conditional Kendall’s tau; Cox1, adjusted transformation via Cox model with continuous T′(a); Cox2, adjusted transformation via Cox model with the first and second tertiles of T′(a).
The right half of Supplementary Table S5 presents the results of tests of conditional independence between X and T given covariate Z. Conditional independence between T and X given Z is rejected for most of the simulated data sets, which explains why the conventional Cox proportional hazard model adjusting for independent truncation yields large bias for . Jones and Crowley’s method is worse in terms of finite sample performance than the Cox proportional hazards model ignoring the dependence of the truncation times in this particular simulation scenario. The substantial bias in Jones and Crowley’s estimates arises because the simulation model is not consistent with Jones and Crowley’s model. Furthermore, Jones and Crowley’s approach does not adjust for the dependent truncation in its risk-set construction.
The average standard errors in Table 1 are obtained from a nonparametric bootstrap with 500 bootstrap samples. They are close to the corresponding empirical standard errors, with better agreement for n = 500 than for n = 200. Furthermore, the proposed estimator yields empirical coverage probabilities that are generally close to the nominal level of 95%, suggesting that the normal approximation for β is appropriate. The coverage probabilities from the conventional Cox model and Jones and Crowley’s method are much lower than 95%; this is expected given their biased estimation of β.
We also investigated the empirical powers of the proposed methods. With the true value of β = 1, we considered the 1-sided hypothesis test of H0 : β = 0.8 v.s. H1 : β > 0.8. The power analysis for the simulation setup in Section 4.1 is summarized in Table S4 in the supplementary materials. As seen in Table S4, the power of the three proposed methods does decrease somewhat as the censoring rate increases. The power of the Cox model assuming independent truncation is much lower than that of the proposed methods, especially under heavier dependent truncation. The Jones & Crowley method has even lower power than the Cox model assuming independent truncation. This is not surprising since both of the two comparison methods display negative biases in their estimates for β as seen in Table 1, with that of Jones & Crowley’s method being larger in magnitude (i.e., it is closer to or less than the null of 0.8). Furthermore, the power of the two comparison methods increases in general as the censoring rate increases. This is due to the decrease in negative bias under higher censoring rates. As expected, the power increases as the sample size increases.
4.2. Dependence induced by covariates
The dependence between truncation and event times might be induced, in part, by covariates. To study the performance of the proposed methods in this setting, we considered a scenario in which X and T′(a) are dependent unconditional on Z, but quasi-independent conditional on Z. Note that if this model held for X and T, the dependence could be fully addressed using a regression model that adjusted for Z. We again generated X from Model (7), but now took λ0(x) to be a Weibull hazard function with shape 5 and scale 1. Given the same Z, T′(a) was also generated from a Cox model, but with a Weibull baseline hazard function with shape ϕ and scale 1. Since X and T′(a) were generated using the same Z, they are correlated through Z. We used the transformation model T = (1 + a)T′(a) − aX to generate T and repeated this process until we obtained n = 200 or 500 observations that satisfied T ≤ Y = min(X, C), where the censoring time C is an independent Weibull distribution with shape r and scale 1. The parameters (ϕ, a, r) were chosen to achieve 50% truncation proportion, two levels of post-truncation association measured by conditional Kendall’s tau between (T, X)|T ≤ Y of τ = 0.2, 0.35 and two levels of censoring after truncation at 0% and 15%. Each setting was repeated 1000 times. Supplementary Table S1 presents the values for (ϕ, a, r) under each scenario.
The average bias for the transformation parameter estimates and results for the regression coefficient are summarized in Supplementary Table S6 and Table 2, respectively. The CK estimator displays mild to moderate bias for both the transformation parameter and regression coefficient. This is expected because the CK estimator does not account for Z in estimating the parameter a, and thus will not be able to recover the true latent truncation time when the dependence between T′(a) and X is induced by covariate Z. However, the biases are not as severe as those from the conventional Cox model (Cox QI) that falsely assumes independent truncation or from Jones and Crowley’s method (JC) (Jones and Crowley, 1992).
Table 2.
Simulation results under dependence induced by covariates†
| n = 200 | n = 500 | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| τ | Method | bias | ESE | ASE | CP | bias | ESE | ASE | CP |
| censoring = 0% | |||||||||
| 0.2 | Cox QI | −0.081 | 0.092 | 0.097 | 88.2 | −0.083 | 0.059 | 0.059 | 71.5 |
| JC | −0.111 | 0.097 | 0.102 | 82.5 | −0.114 | 0.061 | 0.062 | 56.2 | |
| CK | 0.112 | 0.097 | 0.102 | 85.2 | 0.107 | 0.062 | 0.062 | 63.1 | |
| Cox1 | 0.005 | 0.111 | 0.114 | 96.1 | 0.002 | 0.069 | 0.069 | 95.2 | |
| Cox2 | 0.008 | 0.130 | 0.141 | 96.4 | 0.007 | 0.076 | 0.086 | 95.9 | |
| 0.35 | Cox QI | −0.294 | 0.091 | 0.095 | 16.3 | −0.298 | 0.057 | 0.058 | 0.2 |
| JC | −0.449 | 0.101 | 0.105 | 2.4 | −0.450 | 0.063 | 0.063 | 0.0 | |
| CK | 0.076 | 0.093 | 0.096 | 90.8 | 0.070 | 0.058 | 0.058 | 81.1 | |
| Cox1 | 0.008 | 0.098 | 0.102 | 96.1 | 0.003 | 0.062 | 0.062 | 96.4 | |
| Cox2 | 0.015 | 0.114 | 0.122 | 96.8 | 0.007 | 0.065 | 0.071 | 95.1 | |
| censoring = 15% | |||||||||
| 0.2 | Cox QI | −0.147 | 0.100 | 0.103 | 71.4 | −0.152 | 0.064 | 0.063 | 35.4 |
| JC | −0.189 | 0.105 | 0.109 | 61.1 | −0.195 | 0.067 | 0.066 | 19.6 | |
| CK | 0.126 | 0.133 | 0.140 | 87.0 | 0.124 | 0.080 | 0.082 | 70.2 | |
| Cox1 | −0.016 | 0.169 | 0.177 | 95.3 | −0.013 | 0.106 | 0.101 | 95.2 | |
| Cox2 | −0.017 | 0.166 | 0.176 | 96.2 | 0.001 | 0.111 | 0.129 | 95.8 | |
| 0.35 | Cox QI | −0.201 | 0.097 | 0.097 | 47.9 | −0.199 | 0.060 | 0.060 | 12.1 |
| JC | −0.340 | 0.108 | 0.107 | 14.4 | −0.334 | 0.065 | 0.065 | 0.2 | |
| CK | 0.053 | 0.106 | 0.107 | 93.8 | 0.056 | 0.069 | 0.066 | 88.7 | |
| Cox1 | −0.013 | 0.115 | 0.113 | 95.4 | −0.010 | 0.074 | 0.071 | 94.5 | |
| Cox2 | 0.000 | 0.117 | 0.128 | 96.6 | −0.005 | 0.076 | 0.077 | 95.1 | |
τ, the post-truncation conditional Kendall’s tau; bias, empirical bias; ESE, empirical standard error; ASE, average of bootstrap standard error with size 500; CP, coverage (%) of 95% Wald confidence interval; JC, Jones & Crowley’s method; CK, unadjusted transformation via conditional Kendall’s tau; Cox1, adjusted transformation via Cox model with continuous T′(a); Cox2, adjusted transformation via Cox model with the first and second tertiles of T′(a).
On the other hand, the Cox adjusted transformation approaches, Cox1 and Cox2, which estimate a through a Cox model that uses T′(a) as the truncation variable and adjusts for Z, yield virtually unbiased estimates for both the transformation parameter and the regression coefficient under all scenarios. Also, the truncation rate does not appear to have much impact on the performance of the proposed Cox adjusted transformation approaches in terms of empirical bias, as seen by comparing results in Tables 1 and 2, in which the truncation rates are 30% and 50%, respectively. More important than the truncation rate is the strength of dependence between X and T.
For all three proposed methods, the average standard errors obtained from the bootstrap approach with 500 bootstrap samples are reasonably close to the empirical standard errors. However, the empirical coverage probabilities of the regression coefficients are closer to the anticipated level of 95% for the two adjusted transformation approaches than for the conditional Kendall’s tau estimator. Since the Cox adjusted approaches perform well in scenarios with and without the covariate induced dependence in X and T′(a), our results suggest that they are more robust than the conditional Kendall’s tau estimator and should be preferred.
4.3. Sensitivity analysis to model misspecification
The performance of the proposed estimator when the linear transformation model does not hold is also of interest. In one such case, we generated X and T under a Clayton copula (Clayton, 1978) with parameter θ. The Kendall’s tau between X and T equals θ/(θ + 2). The marginal distributions of X and T are derived from equation (7). Specifically, we took λ0(x) to be the Weibull hazard function with shape 2 and scale 0.75 for generation of X, and λ0(t) to be the Weibull hazard function with shape ϕ and scale 1.0 for the generation of T. We used two levels of post-truncation dependence as measured by conditional Kendall’s tau values of 0.2 and 0.35. We generated censoring times from an independent Weibull distribution with shape r and scale 1. The process was repeated until we obtained n = 200 or 500 observations that satisfied T ≤ Y = min(X, C). The parameters, p and r, were chosen to maintain 40% and 60% truncation proportion at two levels of censoring 0% and 15%, respectively. The values of parameters (ϕ, θ, r) are listed in Supplementary Table S1. We generated 1000 such datasets. Figure 2 displays scatter plots of X − T versus X with no censoring, for randomly generated samples of 500 observations with X > T. The post-truncation conditional Kendall’s tau is 0.2 (left panel) or 0.35 (right panel). Our proposed goodness-of-fit test in Section 2.3 is not suitable in detection of model misspecification here as linearity between X − T and X holds approximately in the observable region.
Fig. 2.
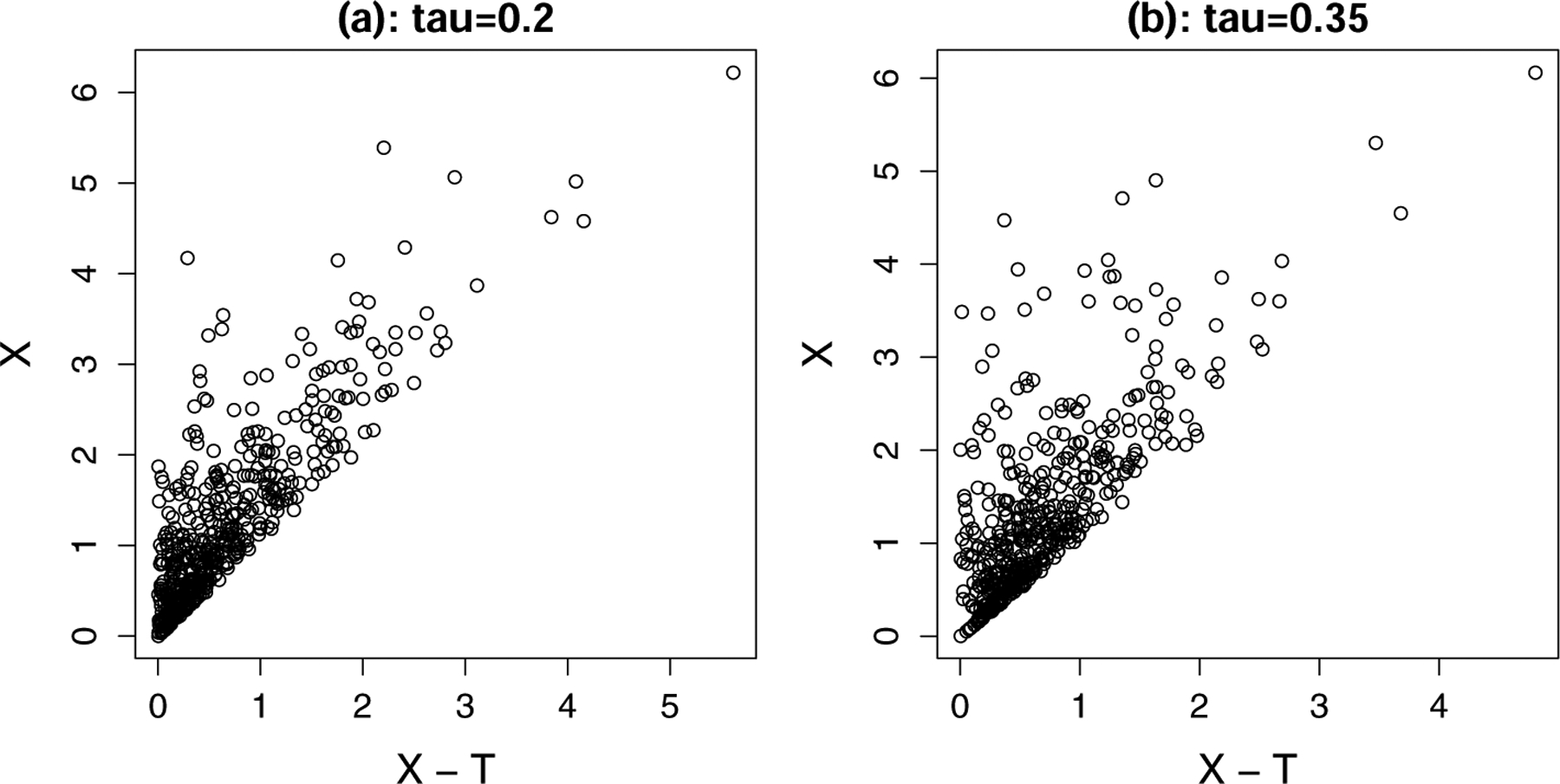
Scatter plots of X − T vs. X given X > T. The plot on the left has post-truncation conditional Kendall’s tau of 0.2, and that on the right has conditional Kendall’s tau of 0.35.
Table 3 lists the values of the minimized parameter averaged across simulations for each of the three proposed methods, i.e., conditional Kendall’s tau under CK estimator, the coefficient α in equation (4) under Cox1, and the ℓ2 norm of α in equation (4) under Cox2. We also tested the existence of the residual quasi-dependence for each of the three proposed methods. We considered a Cox proportional hazard model adjusting for independent left truncation T′(a), and included the first and second tertiles of T′(a), i.e., and , as covariates in addition to other covariates Z. If conditional independence between X and T′(a) given Z holds, then the regression coefficients of and will be zero. We use a global likelihood ratio test with two degrees of freedom to assess whether the regression coefficients of and are significantly different from zero. We reported the power of the test in Table 3. When τ = 0.35 and there is no censoring, the ℓ2 norm of α under Cox2 is 0.391 (or 0.482) for n = 200 (or 500), which suggests that residual dependence between the failure time and transformed truncation time may still exist after the transformation. When τ = 0.35, censoring is 0% and n = 500, the power of the test for residual quasi-dependence is 100%, 100% and 92.5% for the CK estimator, Cox1, and Cox2, respectively, which explains why these methods yield large bias in this simulation scenario (Table 4). In addition, we checked if the transformation parameter a is close to −1, in which case the transformation model would not be appropriate. It turns out that transformation model is not appropriate only for a small fraction of simulated datasets. The simulation results in Table 3 suggest the importance of goodness-of-fit assessment for the linear transformation model as proposed in Section 2.3, especially when the strength of correlation between X and T is strong.
Table 3.
Summary of statistics for goodness-of-fit assessment under the misspecified model†
| n = 200 | n = 500 | ||||||
|---|---|---|---|---|---|---|---|
| τ | cen | CK | Cox1 | Cox2 | CK | Cox1 | Cox2 |
| value of minimized parameter | |||||||
| 0.2 | 0% | −0.019 | <0.001 | 0.136 | −0.006 | <0.001 | 0.128 |
| 15% | 0.078 | <0.001 | 0.171 | −0.008 | <0.001 | 0.137 | |
| 0.35 | 0% | −0.044 | <0.001 | 0.391 | −0.009 | <0.001 | 0.482 |
| 15% | −0.018 | <0.001 | 0.234 | −0.011 | <0.001 | 0.269 | |
| proportion of test with p-val < 0.05 | |||||||
| 0.2 | 0% | 49.6 | 15.5 | 10.4 | 96.2 | 42.8 | 12.2 |
| 15% | 81.7 | 66.7 | 19.3 | 94.1 | 76.9 | 21.2 | |
| 0.35 | 0% | 99.0 | 84.3 | 43.7 | 100.0 | 100.0 | 92.5 |
| 15% | 93.4 | 79.5 | 32.2 | 99.6 | 94.6 | 73.0 | |
| proportion of transformation parameter a < −0.95 | |||||||
| 0.2 | 0% | 0 | 0 | 0 | 0 | 0 | 0 |
| 15% | 0 | 0.2 | 0.1 | 0 | 0.1 | 0 | |
| 0.35 | 0% | 0 | 0 | 2.7 | 0 | 0 | 1.0 |
| 15% | 0 | 0.3 | 0.3 | 0 | 0 | 0 | |
CK, unadjusted transformation via conditional Kendall’s tau; Cox1, adjusted transformation via Cox model with continuous T′(a); Cox2, adjusted transformation via Cox model with the first and second tertiles of T′(a).
Table 4.
Summary of simulation under the misspecified model†
| n = 200 | n = 500 | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| τ | Method | bias | ESE | ASE | CP | bias | ESE | ASE | CP |
| censoring = 0% | |||||||||
| 0.2 | Cox QI | −0.095 | 0.095 | 0.095 | 83.5 | −0.100 | 0.054 | 0.058 | 62.4 |
| JC | −0.046 | 0.106 | 0.105 | 93.6 | −0.056 | 0.059 | 0.064 | 88.9 | |
| CK | −0.020 | 0.097 | 0.097 | 94.6 | −0.027 | 0.056 | 0.060 | 94.9 | |
| Cox1 | 0.007 | 0.104 | 0.104 | 95.8 | 0.001 | 0.061 | 0.064 | 96.0 | |
| Cox2 | 0.024 | 0.117 | 0.124 | 95.5 | 0.022 | 0.062 | 0.071 | 97.1 | |
| 0.35 | Cox QI | 0.151 | 0.115 | 0.114 | 77.1 | 0.143 | 0.075 | 0.071 | 51.0 |
| JC | 0.500 | 0.185 | 0.171 | 22.2 | 0.441 | 0.118 | 0.107 | 6.0 | |
| CK | 0.237 | 0.130 | 0.127 | 56.4 | 0.226 | 0.083 | 0.080 | 22.3 | |
| Cox1 | 0.193 | 0.138 | 0.134 | 82.9 | 0.193 | 0.087 | 0.084 | 57.9 | |
| Cox2 | 0.187 | 0.195 | 0.195 | 85.4 | 0.164 | 0.155 | 0.146 | 78.8 | |
| censoring = 15% | |||||||||
| 0.2 | Cox QI | −0.109 | 0.108 | 0.109 | 82.2 | −0.125 | 0.068 | 0.066 | 54.4 |
| JC | −0.050 | 0.120 | 0.122 | 93.9 | −0.080 | 0.075 | 0.073 | 81.1 | |
| CK | −0.062 | 0.145 | 0.142 | 92.6 | −0.072 | 0.089 | 0.086 | 86.7 | |
| Cox1 | −0.036 | 0.155 | 0.152 | 94.6 | −0.044 | 0.095 | 0.093 | 91.9 | |
| Cox2 | −0.031 | 0.178 | 0.190 | 95.4 | −0.029 | 0.097 | 0.106 | 95.6 | |
| 0.35 | Cox QI | 0.027 | 0.129 | 0.131 | 95.1 | 0.015 | 0.079 | 0.079 | 95.0 |
| JC | 0.197 | 0.163 | 0.166 | 82.6 | 0.158 | 0.100 | 0.099 | 67.2 | |
| CK | 0.080 | 0.170 | 0.169 | 94.7 | 0.070 | 0.104 | 0.104 | 91.1 | |
| Cox1 | 0.090 | 0.180 | 0.178 | 93.8 | 0.084 | 0.110 | 0.109 | 92.5 | |
| Cox2 | 0.099 | 0.207 | 0.214 | 95.8 | 0.111 | 0.130 | 0.136 | 91.2 | |
τ, the post-truncation conditional Kendall’s tau; bias, empirical bias; ESE, empirical standard error; ASE, average of bootstrap standard error with size 500; CP, coverage (%) of 95% Wald confidence interval; JC, Jones & Crowley’s method; CK, unadjusted transformation via conditional Kendall’s tau; Cox1, adjusted transformation via Cox model with continuous T′(a); Cox2, adjusted transformation via Cox model with the first and second tertiles of T′(a).
Table 4 summarizes the average biases for the regression coefficient from the proposed estimators. The proposed estimators yield mild bias in some cases due to the misspecification of the dependent structure. In general, the stronger the association between X and T is, the larger the bias. Among the three proposed estimators, the adjusted transformation via Cox model estimators generally have relatively smaller biases than the CK estimator, suggesting that the adjusted transformation estimators are more robust to model misspecification than the CK estimator. The standard errors obtained from the nonparametric bootstrap approach with 500 bootstrap samples yield reasonable estimates when comparing to their empirical counterparts. When the conditional Kendall’s tau in Clayton copula is 0.35, the biases for all three proposed estimators decrease as censoring rate increases. This is because the misspecified dependence structure is diluted by the censoring, as there are fewer pairs of uncensored (X, T) available for the transformation model estimation procedure. When the association between X and T is moderate, i.e., τ = 0.2, the biases from the proposed estimators are smaller than that of the conventional Cox model that falsely assumes quasi-independence and than that of the Jones & Crowley method; with the bias for Jones & Crowley’s method being smaller than that of the conventional Cox model ignoring dependent truncation. As the strength of the dependence becomes stronger, the biases of the proposed estimators can be slightly larger than those from the conventional Cox model, but still smaller than those from Jones & Crowley’s method. This is not surprising, given the detectable lack of fit of the transformation model to this copula scenario under heavy dependence (Table 3). The larger bias from Jones and Crowley’s approach compared to that of the proposed methods when τ = 0.35 suggests that the Jones and Crowley model adjusts for less of the dependence deriving from the copula model than does the transformation model.
As a second example of model misspecification, we applied our proposed methods and the two comparison methods to 1000 randomly generated datasets from a Jones and Crowley’s model λ(x|z) = λ0(x) exp(αt + βz) with conditional Kendall’s tau 0.20 and n = 200. We found that Jones and Crowley’s approach yields unbiased estimate for β = 1, while the estimate for β from Cox proportional hazards regression adjusting for quasi-independent left truncation has significant bias. The proposed methods also do not perform well because this simulation scenario does not satisfy the transformation model. We are able to identify this through our goodness of fit tests. Specifically, the global likelihood ratio test as used in Table 3 rejected the conditional independence between X and T′(a) for the proposed CK, Cox1 and Cox2 approaches 100%, 99.9% and 97.3% times out of the 1000 replications, respectively.
Although these are just two examples of misspecified models, they illustrate the usefulness of the tools that are available for goodness of fit, and teach us that we should be more concerned about deviations from the model in the presence of light censoring versus heavy censoring.
5. Applications to Alzheimer’s disease studies
First, we applied the proposed methods to a National Alzheimer’s Coordinating Center (NACC) autopsy sample, in which the event time of interest is subject to right truncation (Section 5.1). Next, we illustrated the proposed methods through a NACC cohort, in which the event time of interest is left-truncated and right-censored (Section 5.2).
5.1. An NACC autopsy sample subject to right truncation
The NACC database contains numerous clinical, neuropsychological and demographic variables on thousands of participants from Alzheimer’s disease research centers across the United States (Beekly et al., 2007). Participants undergo a baseline visit and approximately annual follow-up visits in which a Uniform Data Set is completed, including demographic, standard motor, behavioral, functional and neuropsychological assessments. Participants also have the opportunity to donate their brain upon death for research purposes, which include a neuropathological evaluation. We focus on the 2005–2014 autopsy sample from the NACC database, which consists of 1402 subjects satisfying: no primary neuropathological diagnosis other than Alzheimer’s disease neuropathological changes at autopsy, no impairment due to alcohol use, depression, medical use, or medical illness, available Braak stage for neurofibrillary degeneration and density of neocortical neuritic plaques, age of death ≥ 50 years. The 215 patients with missing information in either APOE genotype or education were removed from the analysis.
It is of interest to analyze the time from NACC entry to death (in years), and in particular, its association with age at entry (in years), years of education, sex and APOE e4 genotype. This time is right-truncated by the time from NACC entry to data extraction. The untruncated population here are NACC participants who had or will have an autopsy. Among those who ultimately have an autopsy, we lose those with longer survival times. To accommodate right truncation, we reverse the time scale following the procedure outlined in the beginning of Section 2 to yield left truncation. We rejected the null hypothesis of quasi-independence (, p-value p < 0.001), though the magnitude of the association is notably small. Furthermore, based on the global likelihood ratio test described in the Supplementary Material, we rejected the conditional independence between time to death and time to data extraction given covariates (p < 0.001).
We implemented our proposed methods and the conventional Cox model that falsely assumes quasi-independence. We carried out the procedures described in Section 2.3 to assess the goodness-of-fit of the linear transformation model. Specifically, the piecewise truncated regression yields chi-squared p-values of 0.064 and < 0.001 for one and two breakpoints, respectively. This suggests that the linear transformation model may be inadequate for this data. Therefore, we divided the full data into three equally populated segments: X ∈ (0, 2.734), X ∈ [2.734, 5.468) and X ∈ [5.468, ∞) and applied the transformation model separately to each of the three subsets.
It is also possible that there remained residual dependence even after application of the transformation model. We assessed this by including T′(a) from each of three proposed methods in the form W{T′(a)} = (W1, W2)⊤ in equation (4), in addition to the other covariates (i.e., gender, age, education and APOE genotype). W1 and W2 are 0–1 variables with W1 = 1 if T′(a) falls under the first tertile and W2 = 1 if T′(a) falls between the first and the second tertiles. For the CK approach, the regression coefficients of W1 and W2 are and , and the ℓ2 norm of is . For the Cox1 approach, and , and . For the Cox2 approach, and , with . These results suggest that there is residual dependence based on the CK and Cox1 approaches. There is possible residual dependence for the Cox2 approach, with relative small values of and moderate to large p-values.
We implemented our proposed methods and the conventional Cox model that falsely assumes quasi-independence; results are presented in Table 5. We calculated standard errors using the simple bootstrap with 500 samples. Since the analysis was carried out in the reverse time scale, a positive regression coefficient is associated with a lower risk of death. Interestingly, the results are remarkably similar across the four different models: the Cox model assuming independent truncation and the three proposed transformation regression models. This is likely due to the low level of dependence between truncation and event times (τ = 0.09). It is also possible that the linear transformation model does not fully capture the dependence between truncation and event times, and thus does not appreciably impact the estimates.
Table 5.
Summary of analysis of an NACC autopsy sample subject to right truncationy†
| Cox QI | CK | Cox1 | Cox2 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SE | p | SE | p | SE | p | SE | p | |||||
| Failure time: time from NACC entry to death (in years) | ||||||||||||
| X ∈ [0,2.734) | ||||||||||||
| X ∈ [2.734,5.468) | ||||||||||||
| X ∈ [5.468, ∞) | ||||||||||||
| male | −0.169 | 0.062 | 0.00 | −0.170 | 0.064 | 0.01 | −0.170 | 0.072 | 0.02 | −0.172 | 0.060 | 0.01 |
| age | −0.009 | 0.003 | 0.00 | −0.009 | 0.003 | 0.00 | −0.008 | 0.003 | 0.01 | −0.009 | 0.003 | 0.01 |
| education | 0.022 | 0.009 | 0.02 | 0.022 | 0.010 | 0.04 | 0.022 | 0.010 | 0.03 | 0.022 | 0.010 | 0.03 |
| APOE | −0.036 | 0.060 | 0.54 | −0.036 | 0.056 | 0.52 | −0.034 | 0.059 | 0.57 | −0.036 | 0.060 | 0.54 |
CK, unadjusted transformation via conditional Kendall’s tau; Cox1, adjusted transformation via Cox model with continuous T′(a); Cox2, adjusted transformation via Cox model with the first and second tertiles of T′(a); p, the Wald test p-value; age, age at entry (in years). Models are fitted on the reversed time scale.
5.2. An NACC cohort subject to left truncation and right censoring
In another NACC study, the primary aim was to assess how APOE genotype, gender, and other baseline variables are associated with the time from onset of cognitive decline to death. The NACC cohort includes both incident and prevalent cases of cognitive decline. Enrollment in our sample began in September 2005, and follow-up ended in February 2017. The prevalent cases, who entered NACC with a diagnosis of cognitive decline, must be treated as left-truncated for analysis of time from onset of cognitive decline to death, as they had to live long enough to enter NACC. The untruncated population here are individuals who had onset of cognitive decline. We lose those who did not live long enough to enter NACC, i.e., those with shorter survival times. As some subjects dropped out during follow-up or were alive at the end of follow-up, the event time was also subject to right censoring. Of the 7436 participants, 3192 died by the end of the study. Quasi-independence between the truncation time and the failure time is rejected with the conditional Kendall’s tau test (τc = 0.229, p < 0.001). Covariates of interest include participant’s age of onset of cognitive decline (average 72 years), gender (51.1% male), education level (average 15.1 years), APOE e4 genotype (47.3% with e4 allele), the existence of maternal (34.3%) and paternal (17.8%) history of cognitive decline.
We applied our goodness-of-fit assessment using piecewise truncated regression and found that one and two breakpoints were preferred over the fully linear model (both p-values < 0.001). Because of this, we divided the full data into three segments formed by the two breakpoints: X ∈ (0, 6.778), X ∈ [6.778, 13.472) and X ∈ [13.472, ∞). The transformation model was then applied separately to each of the three subsets. After obtaining , we estimated the transformation parameters, the latent truncation times T′(a), and the regression coefficients β based on the pseudo likelihood in equations (5) and (6). The values of the minimized objective functions for the three proposed methods are for the CK approach, for the Cox1 approach, and for the Cox2 approach. These are all close to zero, indicating that we have obtained solutions.
We next assessed whether there is any residual dependence between the event time and transformed truncation time under the piecewise truncated regression models in Table 6. For the CK approach, the regression coefficients of W1 and W2 are and , and . For the Cox1 approach, and , with . These results suggest that residual dependence may still exist after the transformation based on the CK or Cox 1 approaches. For the Cox2 approach, and , which suggests that transformation model based on the Cox2 approach successfully removes the dependent truncation.
Table 6.
Summary of analysis of an NACC cohort subject to left truncation and right censoringy†
| Cox QI | CK | Cox1 | Cox2 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SE | p | SE | p | SE | p | SE | p | |||||
| Failure time: time from onset of cognitive decline to death (in years) | ||||||||||||
| X ∈ (0, 6.778) | ||||||||||||
| X ∈ [6.778,13.472) | ||||||||||||
| X ∈ [13.472,∞) | ||||||||||||
| age | 0.030 | 0.002 | 0.00 | 0.020 | 0.003 | 0.00 | 0.033 | 0.006 | 0.00 | 0.047 | 0.006 | 0.00 |
| MaternalHx | −0.115 | 0.039 | 0.00 | 0.038 | 0.047 | 0.42 | 0.111 | 0.087 | 0.20 | 0.252 | 0.094 | 0.00 |
| PaternalHx | −0.122 | 0.049 | 0.01 | 0.019 | 0.071 | 0.79 | 0.036 | 0.112 | 0.75 | 0.203 | 0.122 | 0.10 |
| male | 0.231 | 0.037 | 0.00 | 0.087 | 0.050 | 0.08 | 0.121 | 0.099 | 0.22 | −0.062 | 0.118 | 0.60 |
| education | −0.012 | 0.005 | 0.03 | −0.005 | 0.008 | 0.54 | −0.001 | 0.014 | 0.94 | 0.028 | 0.016 | 0.09 |
| APOE | −0.056 | 0.036 | 0.12 | −0.127 | 0.054 | 0.02 | −0.113 | 0.093 | 0.23 | −0.248 | 0.112 | 0.03 |
CK, unadjusted transformation via conditional Kendall’s tau; Cox1, adjusted transformation via Cox model with continuous T′(a); Cox2, adjusted transformation via Cox model with the first and second tertiles of T′(a); p, the Wald test p-value. Models are fitted on the reversed time scale.
The results from these analyses are presented in Table 6, where the standard errors were obtained from 500 bootstrap samples. Older age of onset of cognitive decline is associated with a higher risk of death, as suggested by the Cox2 approach . The Cox model assuming independent truncation produced a significant association between risk of death and paternal history of cognitive decline, gender and education, however, the Cox2 estimates of these associations are quite different in magnitude and sign, and are not significant. As shown in the simulations, when there is even moderate censoring, there may be a loss of power. The Cox2 approach suggests that maternal history of cognitive decline is associated with an increased risk of death , and APOE e4 genotype is associated with a decreased risk of death . It is possible that people with APOE e4 were aware of their family history of cognitive decline and thus received diagnoses of cognitive decline earlier in the course of their disease progression, making APOE e4 appear protective. These findings differ in magnitude and direction from those from the independent truncation Cox model, emphasizing the importance of properly accounting for dependent truncation.
6. Discussion
We have proposed a transformation model based regression approaches when the truncation and event times are dependent. Instead of making strong assumptions on the distribution of truncation time or event time, we assumed that there is a latent quasi-independent truncation time that satisfies the transformation model of Efron and Petrosian (1994). Two general approaches were proposed to estimate the transformation parameter depending on whether or not covariates induce the dependence between truncation and event times: one based on the conditional Kendall’s tau and one based on the Cox model. Through simulations, we found that the two proposed approaches have good finite sample performance, and the Cox model based approach (Cox2) that accounts for covariate induced dependence is more robust than the conditional Kendall’s tau approach (CK). In practice, when there is moderate to strong correlation between the event time and the truncation time, it is important to carry out the goodness-of-fit assessment for the linear transformation model as proposed in our paper and illustrated in our simulation studies and NACC data applications. Our approaches use the uncensored event times and adjust for the selection bias through inverse probability weighting by the censoring distribution. The proposed methods allow great flexibility in the sense that the mechanism can be easily adopted into other regression models. As the proposed method deals only with time-invariant covariates, it will be interesting to extend it to allow for exogenous time-dependent covariates. Another interesting extension is to consider alternative transformation models (Chiou et al., 2019).
Supplementary Material
Acknowledgements
This research was supported in part by the Harvard NeuroDiscovery Center, the Harvard Clinical and Translational Science Center NIH UL1 TR001102, NIH CA075971, NIH NS094610, NIH NS048005, NIH P50AG005134, NIH P01AG036694, and NIH P30AG066512. Jing Qian and Sy Han Chiou contributed equally to this work.
The NACC database is funded by NIA/NIH Grant U24 AG072122. NACC data are contributed by the NIA-funded ADCs: P50 AG005131 (PI James Brewer, MD, PhD), P50 AG005133 (PI Oscar Lopez, MD), P50 AG005134 (PI Bradley Hyman, MD, PhD), P50 AG005136 (PI Thomas Grabowski, MD), P50 AG005138 (PI Mary Sano, PhD), P50 AG005142 (PI Helena Chui, MD), P50 AG005146 (PI Marilyn Albert, PhD), P50 AG005681 (PI John Morris, MD), P30 AG008017 (PI Jeffrey Kaye, MD), P30 AG008051 (PI Thomas Wisniewski, MD), P50 AG008702 (PI Scott Small, MD), P30 AG010124 (PI John Trojanowski, MD, PhD), P30 AG010129 (PI Charles DeCarli, MD), P30 AG010133 (PI Andrew Saykin, PsyD), P30 AG010161 (PI David Bennett, MD), P30 AG012300 (PI Roger Rosenberg, MD), P30 AG013846 (PI Neil Kowall, MD), P30 AG013854 (PI Robert Vassar, PhD), P50 AG016573 (PI Frank LaFerla, PhD), P50 AG016574 (PI Ronald Petersen, MD, PhD), P30 AG019610 (PI Eric Reiman, MD), P50 AG023501 (PI Bruce Miller, MD), P50 AG025688 (PI Allan Levey, MD, PhD), P30 AG028383 (PI Linda Van Eldik, PhD), P50 AG033514 (PI Sanjay Asthana, MD, FRCP), P30 AG035982 (PI Russell Swerdlow, MD), P50 AG047266 (PI Todd Golde, MD, PhD), P50 AG047270 (PI Stephen Strittmatter, MD, PhD), P50 AG047366 (PI Victor Henderson, MD, MS), P30 AG049638 (PI Suzanne Craft, PhD), P30 AG053760 (PI Henry Paulson, MD, PhD), P30 AG066546 (PI Sudha Seshadri, MD), P20 AG068024 (PI Erik Roberson, MD, PhD), P20 AG068053 (PI Marwan Sabbagh, MD), P20 AG068077 (PI Gary Rosenberg, MD), P20 AG068082 (PI Angela Jefferson, PhD), P30 AG072958 (PI Heather Whitson, MD), P30 AG072959 (PI James Leverenz, MD).
Footnotes
Supplementary material
Supplemental materials of parameters in simulation setups and additional simulation results are available online. An R package, tranSurv, for implementation of the method, is available at https://CRAN.R-project.org/package=tranSurv.
Contributor Information
Jing Qian, University of Massachusetts, Amherst,USA..
Sy Han Chiou, University of Texas at Dallas, Richardson, USA..
Rebecca A. Betensky, New York University, New York, USA.
References
- Austin MD and Betensky RA (2014) Eliminating bias due to censoring in Kendall’s tau estimators for quasi-independence of truncation and failure. Computational Statistics & Data Analysis, 73, 16–26. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beaudoin D and Lakhal-Chaieb L (2008) Archimedean copula model selection under dependent truncation. Statistics in Medicine, 27, 4440–4454. [DOI] [PubMed] [Google Scholar]
- Beekly DL, Ramos EM, Lee WW, Deitrich WD, Jacka ME, Wu J, Hubbard JL, Koepsell TD, Morris JC and Kukull WA (2007) The National Alzheimer’s Coordinating Center (NACC) database: The Uniform Data Set. Alzheimer Disease & Associated Disorders, 21, 249–258. [DOI] [PubMed] [Google Scholar]
- Chen C-H, Tsai W-Y and Chao W-H (1996) The product-moment correlation coefficient and linear regression for truncated data. Journal of the American Statistical Association, 91, 1181–1186. [Google Scholar]
- Chiou S and Qian J (2021) tranSurv: Transformation model based estimation of survival and regression under dependent truncation and independent censoring. URL: http://github.com/stc04003/tranSurv. R package version 1.2.2. [DOI] [PMC free article] [PubMed]
- Chiou SH, Austin M, Qian J and Betensky RA (2019) Transformation model estimation of survival under dependent truncation and independent censoring. Statistical Methods in Medical Research, 28, 3785–3798. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chiou SH, Qian J and Betensky RA (2018) Permutation tests for general dependent truncation. Computational Statistics & Data Analysis, 128, 308–324. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clayton DG (1978) A model for association in bivariate life tables and its application in epidemiological studies of familial tendency in chronic disease incidence. Biometrika, 65, 141–151. [Google Scholar]
- Cox DR (1975) Partial likelihood. Biometrika, 269–276. [Google Scholar]
- Efron B and Petrosian V (1994) Survival analysis of the gamma-ray burst data. Journal of the American Statistical Association, 89, 452–462. [Google Scholar]
- Emura T and Murotani K (2015) An algorithm for estimating survival under a copula-based dependent truncation model. Test, 24, 734–751. [Google Scholar]
- Emura T and Wang W (2010) Testing quasi-independence for truncation data. Journal of Multivariate Analysis, 101, 223–239. [Google Scholar]
- — (2012) Nonparametric maximum likelihood estimation for dependent truncation data based on copulas. Journal of Multivariate Analysis, 110, 171–188. [Google Scholar]
- — (2016) Semiparametric inference for an accelerated failure time model with dependent truncation. Annals of the Institute of Statistical Mathematics, 68, 1073–1094. [Google Scholar]
- Emura T, Wang W and Hung H-N (2011) Semi-parametric inference for copula models for truncated data. Statistica Sinica, 21, 349–67. [Google Scholar]
- Jones MP and Crowley J (1992) Nonparametric tests of the Markov model for survival data. Biometrika, 79, 513–522. [Google Scholar]
- Karlsson M (2006) Estimators of regression parameters for truncated and censored data. Metrika, 63, 329–341. [Google Scholar]
- Lagakos S, Barraj L and De Gruttola V (1988) Nonparametric analysis of truncated survival data, with application to AIDS. Biometrika, 75, 515–523. [Google Scholar]
- Lakhal-Chaieb L, Rivest L-P and Abdous B (2006) Estimating survival under a dependent truncation. Biometrika, 93, 655–669. [Google Scholar]
- Martin EC and Betensky RA (2005) Testing quasi-independence of failure and truncation times via conditional Kendall’s tau. Journal of the American Statistical Association, 100, 484–492. [Google Scholar]
- Qian J and Betensky RA (2014) Assumptions regarding right censoring in the presence of left truncation. Statistics and probability letters, 87, 12–17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rodríguez-Girondo M and de Uña-Álvarez J (2012) A nonparametric test for Markovianity in the illness-death model. Statistics in Medicine, 31, 4416–4427. [DOI] [PubMed] [Google Scholar]
- — (2016) Methods for testing the Markov condition in the illness-death model: A comparative study. Statistics in Medicine, 35, 3549–3562. [DOI] [PubMed] [Google Scholar]
- Tsai W-Y (1990) Testing the assumption of independence of truncation time and failure time. Biometrika, 77, 169–177. [Google Scholar]
- Tsui K-L, Jewell NP and Wu C (1988) A nonparametric approach to the truncated regression problem. Journal of the American Statistical Association, 83, 785–792. [Google Scholar]
- de Uña-Álvarez J (2012) On the Markov three-state progressive model. In Recent Advances in System Reliability, 269–281. Springer. [Google Scholar]
- Vakulenko-Lagun B, Qian J, Chiou SH and Betensky RA (2019) Nonidentifiability in the presence of factorization for truncated data. Biometrika, 106, 724–731. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vakulenko-Lagun B, Qian J, Chiou SH, Wang N and Betensky RA (in press) Nonparametric estimation of the survival distribution under covariate-induced dependent truncation. Biometrics, doi: 10.1111/biom.13545. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


