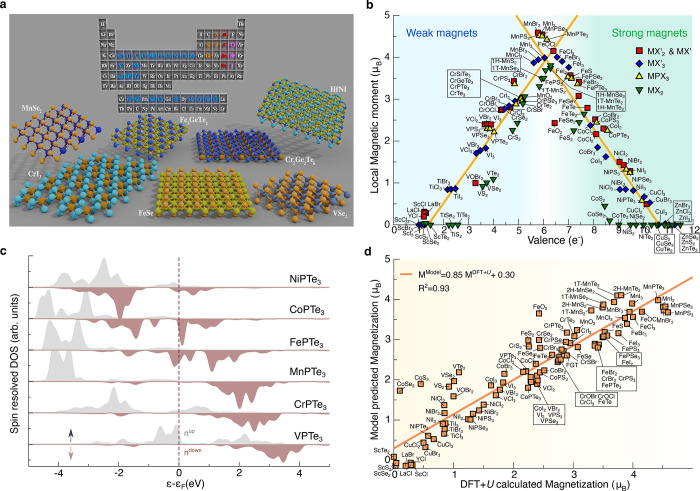
Figure 76.
Slater-Pauling or volcano plot for 2D magnets. (a) High-throughput screening undertook over several crystal structures and elements of the periodic table including formulas MX′2, MX, MX′3, MPX3, MX2, and CrFTe3 with M = Sc–Zn, La, Y; X′=Cl, Br, I; X=O, S, Se, Te; F=Si, Ge. The simulations included mainly transition metals with 3d electrons, but some with 4d and 5d were included for comparison. (b) Variation of the local magnetic moment M(μB) at the metal atom as function of its valence Z(e–). Bader charge analysis was used to extract Z for each metal atom at the compound. The solid lines show a fit to the data set on two different regimes according to the filling of the valence. The positive slope (weak magnets) can be fairly well fitted using M+ = 0.84Z – 1.15 (with a linear regression coefficient R2 = 0.96) and the negative (strong magnets) with M– = −0.87Z + 9.27 (R2 = 0.90). An electron counting argument can be used to explain both regimes as discussed in the text. (c) Spin resolved density of states (DOS) for monolayer MPTe3 (M = V, Cr, Mn, Fe, Co, Ni) as function of the energy ε displaying the spin up density nup (faint gray) and spin down ndown (faint brown) at opposite sides. The energy is shifted to the Fermi energy εF at zero. (d) Variation of the model predicted magnetization versus DFT + U calculated magnetization for the compounds showed in (a). Calculations were performed using the VASP code884 using a 21 × 21 × 1 k-sampling grid, the Dudarev (GGA+U) scheme885 with Hubbard U values following those in ref (341). The energy cutoff is set to 600 eV, the convergence criteria for energy to 10–7 eV and for the forces to 0.01 eV/Å. In order to avoid interactions between the layers, we applied periodic boundary conditions with a vacuum space of 25 Å. We used the projector augmented wave (PAW)886 methods with a plane wave basis. The Vosko–Wilk–Nusair modification scheme887 is applied for the spin-polarized calculations. All images in this figure are original, and no permissions are required.