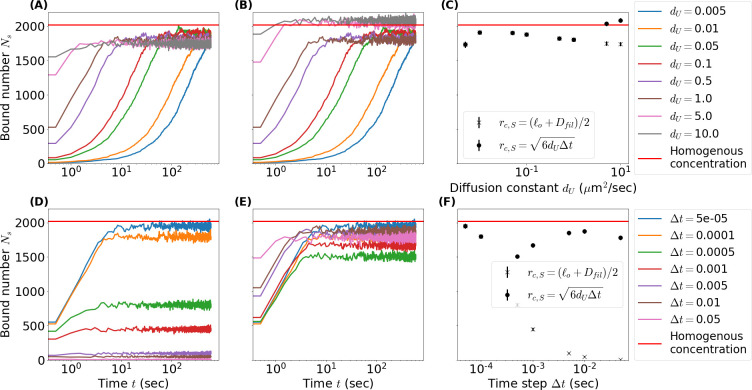
Appendix 2—figure 2. Comparison of initially unbound passive crosslinkers binding to a $1\mathrm{\mu }\mathrm{m}$ filament with binding radii set to a crosslinker’s radius of gyration versus a binding radius $\sim \sqrt{d_U\mathrm{\Delta }t}$.

(A, D) Number of singly bound crosslinkers over time as the unbound diffusion constant $d_U$ (A) and time step $\mathrm{\Delta }t$ (D) vary while binding radius remains unchanged $r_{c,S}=({\mathrm{\ell }}_o+D_{\mathrm{fil}})/2$. Red lines mark the steady-state number of singly bound crosslinkers for a homogeneous reservoir calculated from equations (26)-(30). (B, E) Same as A and D but binding radius scales as the root mean square of diffused distance in a time step $r_{c,S}=\sqrt{6d_U\mathrm{\Delta }t}$. (C, F) Comparison of the steady-state number of singly bound crosslinkers as a function of $d_U$ (C) and $\mathrm{\Delta }t$ (F) for both definitions of $r_{c,S}$. Simulation parameters: periodic box length $=2\mathrm{\mu }\mathrm{m}$, filament length $L=1\mathrm{\mu }\mathrm{m}$, linear binding site density $ϵ=27\mathrm{\mu }{\mathrm{m}}^{-1}$, crosslinker number $N=4000$, crosslinker length ${\mathrm{\ell }}_o=50\mathrm{nm}$, association constant $K_{\mathrm{a}}=90.9{(\mu \mathrm{mol}/\mathrm{L})}^{-1}$, unbinding rate ${\displaystyle k_{\mathrm{o},S}=5{\mathrm{s}}^{-1}}$. Unless otherwise stated unbound diffusion constant $d_U=1\mathrm{\mu }{\mathrm{m}}^2/\mathrm{s}$ and timestep $\mathrm{\Delta }t=0.0001\mathrm{s}$