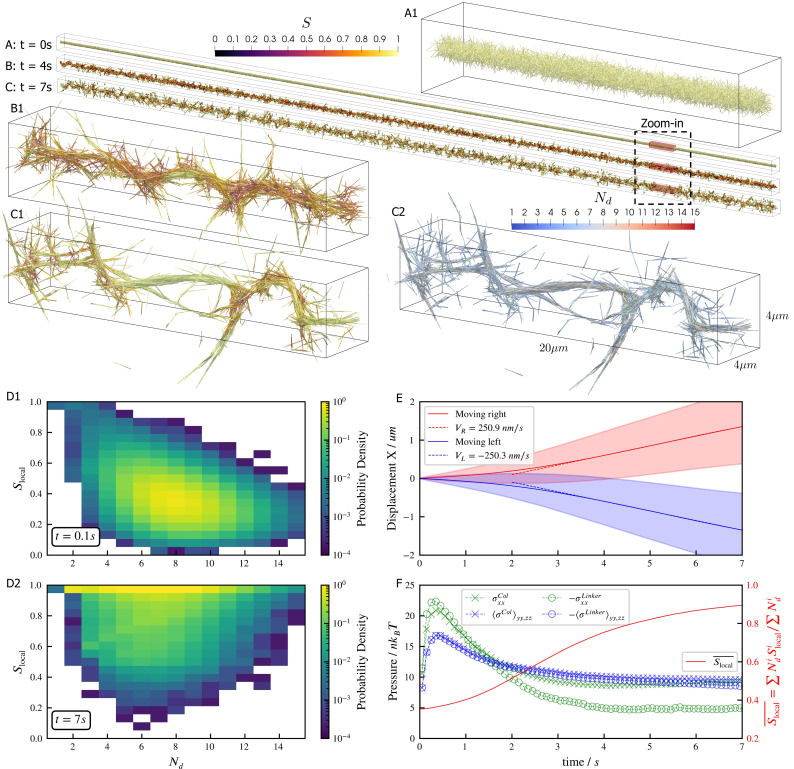
Figure 5. Results for the bundling-buckling simulation of 100,000 microtubules and 500,000 dynein motors in the periodic simulation box of $600\times 10\times 10\mathrm{\mu }\mathrm{m}$.

Brownian motion of microtubules is turned off. Each dynein has one non-motile head permanently attached to a microtubule and the other motile head walks processively with maximum velocity $1\mathrm{\mu }\mathrm{m}{\mathrm{s}}^{-1}$. If bound, the motile head moves toward the microtubule minus-end, and detaches upon reaching it. Detailed parameters for this motor are tabulated in the Appendix 1. Every microtubule has 5 dynein motors permanently attached to randomly chosen, fixed locations along the length. The initial configuration of microtubules is randomly generated, with their orientations sampled from an isotropic distribution and centers uniformly distributed within a cylinder of length $600\mathrm{\mu }\mathrm{m}$ and diameter $0.3\mathrm{\mu }\mathrm{m}$. The motile heads of all dynein motors are unbound initially. (A, B, C) The bundle at $t=0\mathrm{s}$, $4\mathrm{s}$, and $7\mathrm{s}$. Microtubules are colored by their local nematic order parameter $S_{\mathrm{local}}=\sqrt{\frac{3}{2}{Q}_{ij}{Q}_{ij}}$, with $Q_{ij}=⟨p_i{p}_j⟩-\frac{1}{3}{\delta }_{ij}$, ${\displaystyle \mathit{p}}$ being the unit orientation vector of each microtubule pointing from the minus to the plus end, and ${\displaystyle \mathit{\delta }}$ the Kronecker delta tensor. The average $⟨.⟩$ is taken over each microtubule plus all microtubules that are directly crosslinked to it by dynein motors. (A1, B1, and C1) Zoom-in views of the small region marked by red box in A, B, and C. (C2) The same region in C1 but colored by $N_d$, the number of microtubules averaged over when computing $S_{\mathrm{local}}$. (D1 and D2) The joint probability distributions $S_{\mathrm{local}}$ and $N_d$ for each microtubule for the entire systems at $t=0.1\mathrm{s}$, when the dyneins crosslink microtubules but microtubules barely move from initial configuration, and at $t=7\mathrm{s}$, when the bundle is nematic. (E) The average trajectories (solid lines) and their standard deviation (shaded area) of left-moving and right-moving microtubules. Dashed lines show linear fits to the average trajectory after $t=4\mathrm{s}$, with results $V_R\approx V_L\approx 250\mathrm{nm}{\mathrm{s}}^{-1}$. (F) The normal stresses and the weighted average $\overline{S_{\mathrm{local}}}$ over time. Due to the symmetry in the $y,z$ directions, only their average is shown ${⟨\sigma ⟩}_{yy,zz}=\frac{1}{2}\left({\sigma }_{yy}+{\sigma }_{zz}\right)$. Collision stress is positive (extensile) and crosslinker stress is negative (contractile). The weighted average $\overline{S_{\mathrm{local}}}=\sum N_d^i{S}_{\mathrm{local}}^i/\sum N_d^i$.

Figure 5—video 1. Contraction and buckling of a long microtubule-motor bundle.

Download video file ^{(8MB, mp4)}

The bottom panel is a zoom-in view to the area in a gray box in the top panel. The simulation details are described in Section Bundle formation and buckling in a filament band.

Figure 5—video 2. Motor motion and stretching during the contraction and buckling of a long microtubule-motor bundle.

Download video file ^{(12.6MB, mp4)}

This is a zoom-in view to the area in a gray box in the bottom panel in Figure 5—video 1. The simulation details are described in Section Bundle formation and buckling in a filament band.