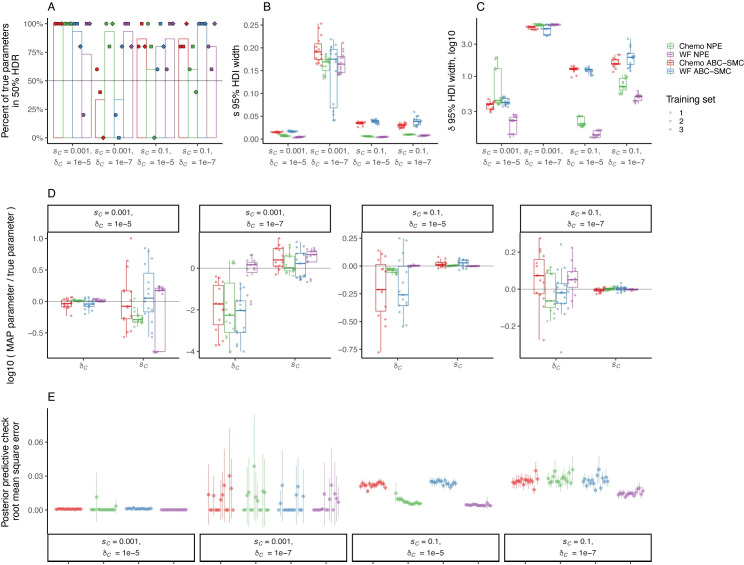
Fig 3. Performance assessment of inference methods using simulated synthetic observations.
The figure shows the results of inference on 5 simulated synthetic observations using either the WF or chemostat (Chemo) model per combination of fitness effect sC and formation rate δC. Simulations and inference were performed using the same model. For NPE, each training set corresponds to an independently amortized posterior distribution trained on a different set of 100,000 simulations, with which each synthetic observation was evaluated to produce a separate posterior distribution. For ABC-SMC, each training set corresponds to independent inference procedures on each observation with a maximum of 10,000 total simulations accepted for each inference procedure and a stopping criteria of 10 iterations or ε < = 0.002, whichever occurs first. (A) The percent of true parameters covered by the 50% HDR of the inferred posterior distribution. The bar height shows the average of 3 training sets. Horizontal line marks 50%. (B, C) Distribution of widths of 95% HDI of the posterior distribution of the fitness effect sC (B) and CNV formation rate δC (C), calculated as the difference between the 97.5 percentile and 2.5 percentile, for each separately inferred posterior distribution. (D) Log ratio of MAP estimate to true parameter for sC and δC. Note the different y-axis ranges. Gray horizontal line represents a log ratio of zero, indicating an accurate MAP estimate. (E) Mean and 95% confidence interval of RMSE of 50 posterior predictions compared to the synthetic observation from which the posterior was inferred. Data and code required to generate this figure can be found at https://doi.org/10.17605/OSF.IO/E9D5X. ABC-SMC, Approximate Bayesian Computation with Sequential Monte Carlo; CNV, copy number variant; HDI, highest density interval; HDR, highest density region; MAP, maximum a posteriori; NPE, Neural Posterior Estimation; RMSE, root mean square error; WF, Wright–Fisher.