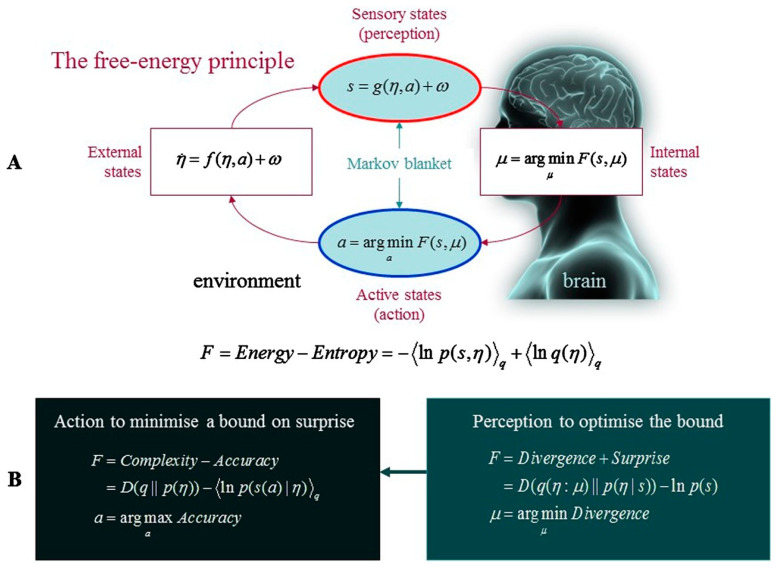
Figure 1.

The free energy principle. (A) Schematic of the quantities that characterise free energy, including a system’s internal states, μ (e.g., a brain), and quantities that describe the system’s exchanges with the environment; specifically, its sensory input, s = g(η,a) + ω, and actions, a, which alter the ways in which the system samples its environment. Environmental states are further defined by equations of motion, $\dot{\eta }$ = f(η,a) + ω, which describe the dynamics of (hidden) states extraneous to the system, η, whereas ω refers to random fluctuations. Under this scheme, internal states and action operate synergistically to reduce free energy, which reflects a function of sensory input and the probabilistic representation (variational density), q(η:μ), that internal states encode. Note that external and internal states are statistically separated by a Markov blanket, which possesses both ‘sensory’ and ‘active’ states. Internal states are influenced by, but cannot affect, sensory states, whereas external states are influenced by, but cannot affect, active states, creating a conditional independence between the system and its environment. (B) Alternative equations that describe the minimisation of free energy. With respect to action, free energy can only be suppressed by the system’s selective sampling of (predicted) sensory input, which increases the accuracy of its predictions. On the other hand, optimising internal states minimises divergence by making the representation an approximate conditional density on the hidden causes of sensory input. This optimisation reduces the free energy bound on surprise, which means that action allows the system to avoid surprising sensations. Reproduced from [8].