Effective case/infection ratio of poliomyelitis in vaccinated populations

SUMMARY

Recent polio outbreaks in Syria and Ukraine, and isolation of poliovirus from asymptomatic carriers in Israel have raised concerns that polio might endanger Europe. We devised a model to calculate the time needed to detect the first case should the disease be imported into Europe, taking the effect of vaccine coverage – both from inactivated and oral polio vaccines, also considering their differences – on the length of silent transmission into account by deriving an ‘effective’ case/infection ratio that is applicable for vaccinated populations. Using vaccine coverage data and the newly developed model, the relationship between this ratio and vaccine coverage is derived theoretically and is also numerically determined for European countries. This shows that unnoticed transmission is longer for countries with higher vaccine coverage and a higher proportion of IPV-vaccinated individuals among those vaccinated. Assuming borderline transmission (R = 1·1), the expected time to detect the first case is between 326 days and 512 days in different countries, with the number of infected individuals between 235 and 1439. Imperfect surveillance further increases these numbers, especially the number of infected until detection. While longer silent transmission does not increase the number of clinical diseases, it can make the application of traditional outbreak response methods more complicated, among others.

INTRODUCTION

Poliomyelitis is an acute viral infectious disease caused by poliovirus, an enterovirus belonging to the family Picornaviridae. Most human poliovirus infections remain asymptomatic, with the infection localized to oropharynx and the gut or symptomatic but only presenting as mild disease with no sign of central nervous system invasion [1]. However, in the remaining 1–2% of cases, poliovirus enters and replicates in the motor neurons of the anterior horn cells of the spinal cord, the brainstem or the motor cortex of the brain, causing destruction of the affected neurons, which results, among other things, in acute flaccid paralysis (AFP) [2].

There are two types of vaccines available against polio: inactivated polio vaccine (IPV) and live attenuated oral polio vaccine (OPV) [3]. OPV provides strong enteric mucosal immunity thereby providing good protection against carriage and shedding of the virus, while IPV results only in systemic immunity protecting against clinical disease, but much less against the enteral shedding of the virus [4].

With the introduction of safe and effective vaccines, polio became a technically eradicable disease [5] and the global efforts led to a marked decrease in disease incidence and the number of endemic countries [6, 7]. However, the very final step towards complete eradication turned out to be especially difficult [8].

In particular, an outbreak at the end of 2013 in the Middle East with 36 cases of polio in Syria and isolation of wild-type poliovirus 1 from sewage and faecal samples from asymptomatic carriers in Israel have raised concerns that the polio might endanger Europe [9]. These fears were widely raised again when circulating vaccine-derived poliovirus 1 caused two cases of polio (as of September 2015) in Ukraine [10].

Recently, Eichner & Brockmann [11] warned that infected individuals can spread the virus unrecognized in an IPV-vaccinated environment (due to the lack of mucosal immunity) and calculated how long the virus can spread across the population, assuming a borderline effective reproduction number R = 1·1, before one AFP case is identified and an outbreak is detected.

They stated, inter alia, that ‘only one in 200 unvaccinated individuals infected with WPV1 will develop acute flaccid paralysis (case/infection ratio C = 0·005)’ and that within n transmission generations, (Rⁿ⁺¹ − 1)/(R − 1) is the cumulative number of infections that are expected to be seen. However, they went on to calculate the number of AFP cases by multiplying those two factors. This – as made explicit by the original authors: ‘[the application of IPV] further reduces the ratio of acute flaccid paralysis to infection’ – is only an approximation, as part of the infected people, in some countries the majority, will be (IPV-) vaccinated. Thus, the ‘effective’ case/infection ratio in an – at least partly – IPV-vaccinated population will be lower, making the results (i.e. the length of unnoticed transmission) even more marked.

Similar problems have already been investigated in the literature, for instance Eichner & Dietz [12] presented a comparable analysis; however, they relied on a stochastic model described with differential equations, which is more realistic, but much less interpretable. In contrast, the simple model of Eichner & Brockmann is more directly interpretable. A novel model will be now devised to take the aforementioned aspect into account, thereby enhancing the validity of the simple model, but still retaining its perspicuity. The consequences of the application of the new model will be illustrated in various European countries using empirical data.

Although borderline transmission (R = 1·1) is assumed throughout the paper, it should be noted that the actual R values are heterogeneous for different populations (depending, for example, on the vaccination coverages), thus this paper describes a conditional calculation, a ‘what-if’ analysis, describing what happens if the importation and silent transmission (R = 1·1) has already occurred.

METHODS

First, a simple model will be discussed where the population is divided into ‘vaccinated’ and ‘unvaccinated’ compartments. After that, the model will be extended to take into account the differences between IPV and OPV.

Two-compartment model

To illustrate our logic, consider first a two-compartment case, i.e. ‘unvaccinated’ and ‘vaccinated’ compartments of the population. A single index case exposes R₀ people to polio, where R₀ denotes the basic reproduction number of the disease. Assuming homogeneous mixing within the population, this will mean R₀·(1 − V) unvaccinated and R₀·V vaccinated people exposed, where V is the proportion of the population vaccinated. Denoting the vaccine's effectiveness against infection (thus, the shedding of the virus) VE_inf, we will have R₀·(1 − V) and R₀·V·(1 − VE_inf) infected people after the first generation in the unvaccinated and vaccinated compartments, respectively. Note that VE_inf is not the ‘traditional’ vaccine effectiveness which is defined as the effectiveness against clinical disease [13]. In the current context, this is related to the mucosal immunity conferred by the vaccine.

Therefore we have

infected in the population after the first generation which will be the effective reproduction number (R) of polio infection; thus we also see that R₀ = R/(1 − V·VE_inf).

At this point, instead of multiplying the number of infected in both compartments by C, the correct calculation goes on to presume that we will have R₀·(1 − V)·C clinical cases only in the unvaccinated compartment; however, in the vaccinated compartment we will have only

manifest cases, where VE_clin represents the effectiveness of the vaccine to protect an already infected subject from developing clinical disease (i.e. it is a conditional probability). In this context, this will be related to the systemic immunity conferred by the vaccine. Thus, the number of clinical cases will be

after the first generation resulting from a single index case.

It should be noted that the usual vaccine effectiveness (i.e. effectiveness against clinical disease) is

Substituting this to the previous formula, we obtain that the number of clinical cases will be

or, equivalently, using the effective instead of basic reproduction number

after the first generation.

After n generations, the number infected will be (Rⁿ⁺¹ − 1)/(R − 1) and not R, therefore the number of clinical cases will be

The factor in parentheses at the right hand side is the correct multiplier that should be used (instead of C). We designate this the effective case/infection ratio, or C_eff, and designate the multiplier of C, i.e. the correction factor that should be used to take the vaccination of the population into account, ϕ_eff. That is, here

and to determine the expected number of transmission generations that are necessary to reach one case of AFP we must solve the equation

with respect to n. Here, R specifies the predetermined level of ‘borderline transmission’, e.g. R = 1·1 as in [11], or any other desired level.

By solving this, we obtain that log_R[1 + (R − 1)/(C·ϕ_eff)] − 1 transmission generations are expected to be needed for the first clinical case to appear, hence the expected time to detect the virus circulation (hereafter designated ‘time-to-detect’), assuming that only AFP surveillance is used, is

where t_gen is the generation time of polio, assumed to be t_gen = 10 days [14]. The number of infected until this time (hereafter designated ‘infected-to-detect’) will be 1/(C·ϕ_eff)

Three-compartment model

The two-compartment approximation is inadequate as it cannot accommodate the IPV and OPV vaccinations, which is a crucial component in real-world settings. Thus, we have to extend this approach to include three compartments: ‘Unvaccinated’, ‘Vaccinated with OPV’ and ‘Vaccinated with IPV’. [The question might be raised whether a ‘Vaccinated sequentially (i.e. IPV followed by OPV)’ compartment is needed. However, the immunity profile conferred by this schedule is similar to the one from the OPV-only schedule [15], so for simplicity we will consider those vaccinated sequentially as if they were vaccinated with OPV.]

It is straightforward to extend the logic seen above for this case (the role of the IPV and OPV compartments is symmetric, but with different coverage and vaccine-effectiveness parameters, which appear as multipliers in the formula), the result will be:

and the equation for the detection of the first AFP case is the same with R≈1·1 and C_eff = C·ϕ_eff again. The formulae to calculate the time-to-detect the first clinical case, and the number of infected until this time is unchanged (with the new ϕ_eff applied).

While this result is theoretically sound, quantitative estimation is bound to run into serious difficulties due to the limited information available to numerically estimate the parameters that appear in the above formulae. Owing to the high variability in the estimates of these parameters, there is no point in aiming to obtain more than an approximate C_eff. We also perform a sensitivity analysis in order to ensure robustness with respect to this uncertainty.

Calculating vaccine coverage

The proportion of the population vaccinated with OPV and IPV (i.e. V^OPV and V^IPV) was calculated using population age distribution as of 1 January 2013. For countries that always used IPV-only schedule, the number of (IPV) vaccinees were calculated exactly for birth years where vaccine coverage was available, for the remaining birth cohorts, the average of all vaccine coverages was assumed as the vaccine coverage. For countries that switched from OPV to IPV, the number of IPV vaccinees were calculated exactly, the number of OPV vaccinees were calculated using the average vaccine coverage for the OPV-only years. We considered that only those who are vaccinated are protected, i.e. we neglected the possible spread of the vaccine virus (which is possible for OPV, but unlikely to play a significant role).

Information on vaccine coverage was extracted from the World Health Organization's Centralized Information System for Infectious Diseases (CISID) [16]. This relies on national coverage reports and WHO/UNICEF coverage estimates, the methodology is described elsewhere [17]. Indicator number 3004 (‘Polio3 – % of infants vaccinated against’) was employed in the present study.

To assess the size of birth cohorts, we used the dataset demo_pjan from Eurostat [18].

The historical changes in vaccination schedules, in particular the switch from OPV to IPV was determined using data from the European Centre for Disease Prevention and Control [9].

Spreadsheet data compiled from the above data sources is presented in Supplementary Table S1.

Calculating vaccine effectiveness

As far as the VE_inf values are concerned, the best information we can use are studies that measured vaccine virus shedding after OPV challenge. From a recent review [19] we can deduce VE^OPV_inf = 0·87 and VE^IPV_inf = 0·19 (by subtracting the odds ratios against shedding presented there from 1). Note that this approach means that for calculation of VE_inf, only the fact of shedding (i.e. whether infection occurred at all or not) is taken into account, but not the duration of shedding or the quantity of shed virus. This can be justified by the currently used definition of VE_inf, in which only the fact of infection matters (duration of shedding and quantity of shed virus is relevant only for the exposure of the environment).

For VE, we can use VE^OPV = VE^IPV = 0·9, which is reasonable for developed countries [20].

Sensitivity analysis

As the parameters used in the devised model (especially VE_inf) are only known with substantial uncertainty, sensitivity analysis was also undertaken, using Monte Carlo simulation [21]. In this approach, the parameters are assumed to have a distribution (as opposed to being fixed values), therefore their functions, such as time-to-detect the first case, will also be random variables. However, the exact distribution of these functions is often unfeasible or impossible to analytically derive from the distribution of the inputs and the functional form, so instead it can be empirically approximated by generating many random variates from the input's distribution, transforming them according to the function, and then estimating the distribution from those transformed variables [21]. This method can be viewed as a way to improve robustness against the uncertainty of the parameters.

In the current case, sensitivity analysis was performed with respect to both VE_inf values. Their distribution was presumed to be independent truncated normal with the mean given by the point estimate already introduced, and the standard deviation being 0·04 for VE^OPV_inf and 0·13 for VE^IPV_inf. These values were chosen so that the resulting distributions' dispersion roughly corresponds to the confidence intervals already known [19]. Truncation was done at [0, 0·9] to ensure that both VE_inf and VE_clin values are between 0 and 1. One million random variates were simulated and the resulting distribution was reconstructed with kernel density estimation [22].

Programs used

Sensitivity analysis, visualization and additional calculations were performed under Wolfram Mathematica v. 10.0 [23]. Full source codes are available from the corresponding author upon request.

RESULTS

Parameter ϕ_eff as a function of vaccine coverages is shown in Figure 1.

Fig. 1.

Parameter ϕ_eff (i.e. the factor with which the case/infection ratio should be multiplied to obtain the effective case/infection ratio in a given population) as a function of vaccine coverage. Panel (a) shows it as a three-dimensional plot; panel (b) depicts the same function as a contour plot, with the colour scale indicating the function value. Red lines in (b) indicate locations of equal (overall) vaccine coverage, with dots depicting selected representative countries (BG, Bulgaria; AT, Austria; FR, France; NO, Norway; NL, The Netherlands).

Table 1 shows the estimated parameters, together with the length of time-to-detect of the first clinical case (i.e. silent transmission) and infected-to-detect that is derived from them.

Table 1.

Estimated vaccine coverage together with ϕ_eff and C_eff parameters calculated from them and the resulting time-to-detect and infected-to-detect for each investigated country

Country	IPV-only introduction	VIPV (%)	VOPV (%)	V (%)	VIPV/V (%)	ϕeff	Ceff	Time-to- detect (days)	Infected-to- detect (days)
Austria	1999	10·32	78·26	88·58	11·65	0·6769	0·003385	349	295
Belgium	2001	13·36	81·82	95·19	14·04	0·5455	0·002727	371	367
Bulgaria	2010	2·66	93·86	96·52	2·76	0·7361	0·003681	340	272
Cyprus	2002	11·75	70·24	81·99	14·33	0·7150	0·003575	343	280
Czech Republic	2007	6·61	91·18	97·79	6·76	0·6174	0·003087	358	324
Denmark	Always	95·05	0·00	95·05	100·00	0·1764	0·000882	487	1134
Estonia	2008	5·45	87·30	92·75	5·88	0·7179	0·003590	343	279
Finland	Always	94·43	0·00	94·43	100·00	0·1830	0·000915	483	1093
France	1990	27·45	63·36	90·81	30·23	0·4606	0·002303	388	434
Germany	1998	12·43	76·48	88·91	13·98	0·6424	0·003212	354	311
Greece	2005	7·79	86·09	93·88	8·30	0·6565	0·003282	352	305
Hungary	2006	6·65	92·39	99·04	6·71	0·5918	0·002959	362	338
Iceland	Always	97·05	0·00	97·05	100·00	0·1552	0·000776	501	1289
Ireland	2001	16·25	65·13	81·38	19·96	0·6649	0·003324	351	301
Italy	2002	9·84	84·20	94·04	10·47	0·6175	0·003088	358	324
Latvia	2009	3·63	91·76	95·39	3·81	0·7263	0·003631	342	275
Lithuania	2005	7·36	82·60	89·96	8·18	0·7118	0·003559	344	281
Luxembourg	2006	7·80	86·70	94·50	8·26	0·6474	0·003237	353	309
Malta	2010	2·66	81·15	83·82	3·17	0·8503	0·004252	326	235
The Netherlands	Always	96·88	0·00	96·88	100·00	0·1570	0·000785	499	1274
Norway	Always	87·15	0·00	87·15	100·00	0·2584	0·001292	448	774
Poland	2008	5·13	91·30	96·43	5·32	0·6743	0·003372	349	297
Portugal	2006	6·28	70·51	76·78	8·17	0·8246	0·004123	329	243
Romania	2008	4·66	90·16	94·82	4·91	0·7092	0·003546	344	282
Slovakia	2005	8·32	90·21	98·53	8·45	0·5678	0·002839	367	352
Slovenia	2003	9·56	84·82	94·37	10·13	0·6175	0·003087	358	324
Spain	2006	7·08	83·90	90·98	7·78	0·7060	0·003530	344	283
Sweden	Always	98·56	0·00	98·56	100·00	0·1390	0·000695	512	1439
UK	2004	10·22	80·78	91·00	11·23	0·6516	0·003258	353	307

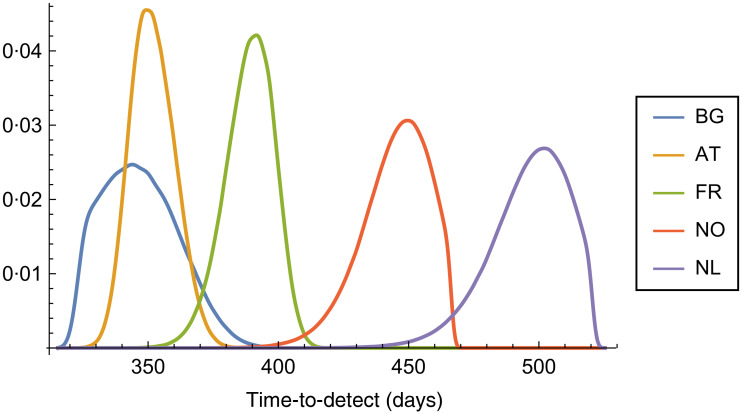
Figure 2 shows the results of sensitivity analysis for time-to-detect in case of a few representative countries (that were chosen to exemplify the practically occurring combinations of vaccine coverages in European countries).

Fig. 2.

Distribution of time-to-detect under parameter uncertainty for selected representative countries (BG, Bulgaria; AT, Austria; FR, France; NO, Norway; NL, The Netherlands).

The Netherlands and Norway represents the IPV-only countries (with relatively high and low IPV coverage, respectively) which have the highest time-to-detect values and also their peaks in Figure 2 are broader than the mostly OPV-vaccinated Western European countries (Austria and France), since they are more sensitive towards the VE^IPV_inf to which a higher standard deviation value was chosen during the sensitivity analysis. Bulgaria represents the Central and Eastern European countries with very high OPV vaccination coverage and hence with the lowest time-to-detect values. The broadness of its peak can be explained by the very low proportion of unvaccinated individuals.

DISCUSSION

The length of silent transmission, i.e. the time needed to detect the first infected by traditional means (i.e. AFP surveillance and not environmental surveillance) depends on vaccine coverage both from OPV and IPV, in a nonlinear way. With all other things being equal, increasing coverage from either of them decreases the effective case/infection ratio (thus increasing the length of unnoticed transmission), but this is almost negligible for OPV, although rather substantial for IPV. If the overall coverage is considered fixed, the effective case/infection ratio radically decreases with increasing proportion of IPV coverage. In other words, the effective case/infection ratio will be lowest for countries where (1) overall vaccine coverage is high and (2) the proportion of IPV within this coverage is also high. Decreasing effective case/infection ratio means increased length of silent transmission (thus increased number of infected until the outbreak is detected), therefore the effect of increasing vaccine coverage might be – in this sense – counterintuitive for time-to-detect and infected-to-detect.

In European countries, assuming borderline transmission (R = 1·1) the length of unnoticed transmission is between 326 days and 512 days using the developed model. In line with the previous remark, those countries are at the lower end, where the overall vaccine coverage is low or the proportion of IPV coverage is low within the overall coverage (e.g. Portugal, Cyprus or Malta on the one hand, and Bulgaria, UK or Germany on the other), and those are at the higher end where the overall vaccine coverage is high and the proportion of IPV coverage within the overall coverage is also high (e.g. The Netherlands, Norway or Denmark).

The range of 326–512 days is in contrast with the results of Eichner & Brockmann [11]; in their article, which neglects the effects of IPV coverage, the length of unnoticed transmission is given as ‘nearly 1 year’ (309 days, precisely). Thus, more elaborate analysis shows that the actual length of silent transmission might be more than 50% longer than what can be derived from the simpler model, depending on the circumstances (i.e. vaccine coverage).

It also instructive to contrast these results with their theoretical limits. For zero vaccine coverage (from both types of vaccines), the effective case/infection ratio will be the same as the traditional case/infection ratio (0·5%), resulting in the already mentioned 309 days, with 200 infections until detection. At the other extreme, with perfect coverage from IPV, the duration of unnoticed transmission is 524 days, with 1620 infections. It can be seen that European countries span the entire spectrum quite well.

It is worth noting that the time-to-detect depends on what R we presume as ‘borderline’ (e.g. R = 1·1), but the ϕ_eff does not, therefore the infected-to-detect also does not, as it only depends on effective C.

Sensitivity analysis reveals some uncertainty in these results due to parameter uncertainty, but qualitatively, the conclusions are left unaffected. For instance, the variation in the time-to-detect the first infected is about ±25–50 days, depending on the exact circumstances.

It should be noted that ‘worst-case’ now means a large number of infected, not a large number of (clinically) ill, so one might wonder whether this phenomenon is worrisome at all. While directly there is no risk of disease involved for the majority of those who are IPV vaccinated even if they are carriers, first, there is always a minority (as the IPV's effectiveness is not 100%, even against clinical disease), and second, not everyone can be vaccinated, for instance due to their age. Moreover, lengthy time until detection can make the traditional outbreak response methods, such as contact tracing, very complicated or downright impossible, thus this is still relevant for public health purposes.

Note that the above calculation assumes that the very first AFP case is detected, and the outbreak is instantly identified (in line with Eichner & Brockmann [11]). This is clearly not a realistic assumption, since the sensitivity of AFP surveillance can never be 100%, even in developed countries [24, 25]. The effect of sensitivity on the investigated outcomes is not linear. To see this, we denote sensitivity with s, then the equation to be solved is not

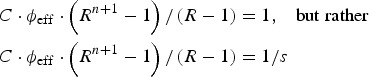(as s sensitivity means that only every (1/s)th case is identified as such). Thus, the actual time-to-detect the outbreak, taking the sensitivity of the surveillance into account is

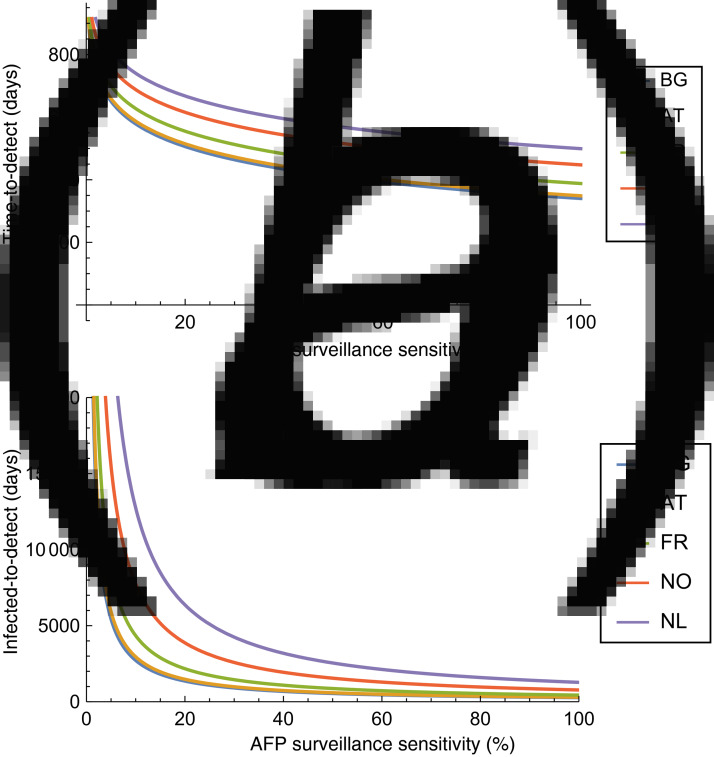
and the number of infected until this point is 1/(Cϕ_effs) using the same logic. This is illustrated on Figure 3 for a few selected European countries. It can be seen that the effect of non-perfect surveillance sensitivity is not substantial up to about 30–40%, and it has much more profound impact on infected-to-detect than on time-to-detect. (Understandably, as the number of cases rises increasingly faster due to geometric growth if more transmission generation is allowed. Imperfect surveillance acts as if ϕ_eff were further decreased.)

Fig. 3.

Impact of the sensitivity of acute flaccid paralysis (AFP) surveillance on the (a) time-to-detect and (b) infected-to-detect for selected representative countries (BG, Bulgaria; AT, Austria; FR, France; NO, Norway; NL, The Netherlands).

Finally, it is important to emphasize that this model in no way predicts the probability of such importation of polio to Europe, i.e. that transmission begins. The calculation of the actual R values (which can be highly heterogeneous for European populations) or the determination of the probability of a continuous transmission (R > 1) are beyond the scope of this paper: R depends on vaccine coverage, contact patterns, demography, hygiene, etc. The presented calculation is conditional, a ‘what-if’ analysis, describing what happens if the importation and silent transmission (R = 1·1) has already occurred. Note that presuming different countries have the same R is unrealistic, thus comparing countries with each other is only valid for infected-to-detect (which does not depend on R) at first glance. Nevertheless, the comparison of time-to-detect still makes sense, as it allows investigation of how IPV and OPV vaccine coverage alters the length of silent transmission in an outbreak.

Naturally, our model has several limitations. One is that countrywide vaccine coverage data were used, which neglects within-country spatial inhomogeneity of vaccine coverage (clustering of unvaccinated individuals), which is otherwise known to be an important factor in disease outbreaks. (This is a violation of the compartmental models' ‘perfect mixing’ assumption.) Due to the fact that the transmission is more likely to start and amplify in such – undervaccinated – clusters, the detection might also be earlier, at least if we assume equal quality of AFP surveillance, even in such clusters. In a similar manner, ‘perfect mixing’ assumption also neglects every stratification of the populations, such as their age and sex distribution; despite the fact that age definitely has a profound impact on the spread of polio. This is, however, unlikely to introduce a systematic error as there are no marked differences in European countries' age and sex composition, apart from the fact that IPV coverage might vary substantially for different age groups. Nevertheless, it would be straightforward to extend the model to incorporate such strata by the introduction of additional compartments (at the price of the introduction of further parameters that are to be estimated), should it be deemed necessary. Finally, the model presumes a deterministic reproduction from generation to generation (i.e. it is governed by the single parameter R). While this is acceptable if R is considered to be an expected value, a finer analysis would be possible by recasting the problem as a, possible multi-type, branching process, which is often applied to describe epidemics [26]. In the branching process approach, the number of secondary infections is considered to be a true random variable (not a single number), allowing more precise modelling, which is valid if the number of infected is small compared to the whole population (as is the case in the present situation). This, however, comes at the price of more complicated mathematical structure.

DECLARATION OF INTEREST

None.