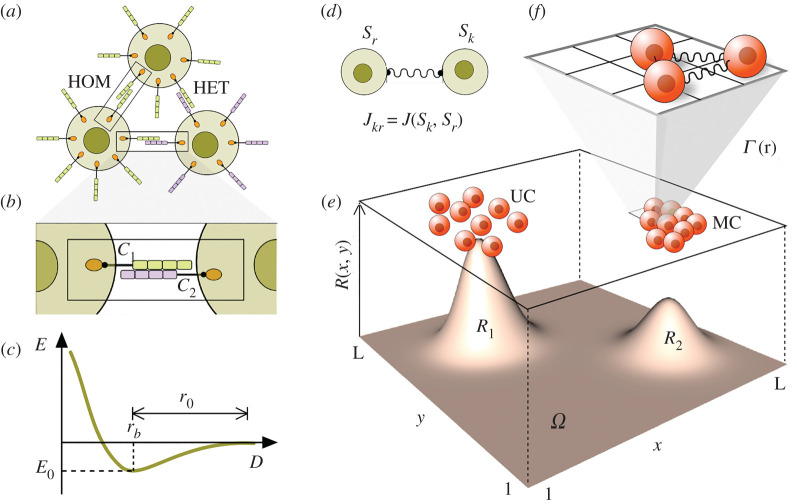
Figure 1.

Cell adhesion and its lattice modelling counterpart. (a) Interactions among cells carrying adhesion molecules (such as cadherins) can involve homologous (HOM) or heterologous (HET), depending on when the molecules are the same or different, respectively [14,15]. The microscopic details (b) of the physical exchanges between cell adhesion molecules (CAM) can be captured by simple physical models where the energy E associated with cell–cell interactions is displayed in (c) against cell–cell distance D. A minimum energy E₀ is associated with a given characteristic scale r_b that would define the equilibrium distance between cells [16,17]. Such energy function (and the underlying forces associated with it) are replaced in this paper by a simple toy model where pairwise interactions are defined by means of a simple coupling coefficient J_kr (d) that weights the strength of the interaction between cells k and f. In this simple way we take into account the heterogeneous nature of evolved CAM and the impact of heterogeneous adhesion [18]. The spatial dynamics of the in silico cells on the $\Omega$ lattice occurs in parallel with the production, decay and continuous diffusion of resources. Different resource abundances (R₁ and R₂) favour the evolution of two main types of behaviour (e), namely unicellular (UC) and multicellular (MC). Interactions occur among nearest neighbours (c) on the 3 × 3 (Moore) neighbourhood (f).