Unveiling the abstract format of mnemonic representations

SUMMARY

Working memory (WM) enables information storage for future use, bridging the gap between perception and behavior. We hypothesize that WM representations are abstractions of low-level perceptual features. However, the neural nature of these putative abstract representations has thus far remained impenetrable. Here, we demonstrate that distinct visual stimuli (oriented gratings and moving dots) are flexibly recoded into the same WM format in visual and parietal cortices when that representation is useful for memory-guided behavior. Specifically, the behaviorally relevant features of the stimuli (orientation and direction) were extracted and recoded into a shared mnemonic format that takes the form of an abstract line-like pattern. We conclude that mnemonic representations are abstractions of percepts that are more efficient than and proximal to the behaviors they guide.

In brief

Kwak and Curtis demonstrate that the memory formats measured with fMRI for two different visual features, orientation and motion direction, are shared in an abstract line-like format. These results demonstrate that the goal-relevant details of past percepts are recoded into abstract working memory representations in the brain.

INTRODUCTION

The precise contents of working memory (WM) can be decoded from the patterns of neural activity in the human visual cortex (Harrison and Tong, 2009; Serences et al., 2009), suggesting that the same encoding mechanisms used for perception also store WM representations (D’Esposito and Postle, 2015). Presumably, representations decoded during memory and perception both reflect activities of neurons selective for encoded stimulus features, and therefore, the representational format of WM is sensory-like in nature (Bettencourt and Xu, 2016; Lorenc et al., 2018; Rademaker et al., 2019). However, patterns during perception of a stimulus are often poor predictors of patterns during WM maintenance. This is especially true in parietal cortex where stimulus-evoked activity fails to predict the contents of WM (Albers et al., 2013; Rademaker et al., 2019). In visual cortex, stimulus-evoked patterns of activity are worse than memory activity at predicting memory content (Harrison and Tong, 2009; Rademaker et al., 2019). Furthermore, under a range of conditions, WM representations in parietal and sometimes even in visual cortices are only slightly impacted by visual distractors (Bettencourt and Xu, 2016; Hallenbeck et al., 2021; Lorenc et al., 2018; Rademaker et al., 2019). Therefore, a reasonable hypothesis is that mnemonic codes are somehow different from perceptual codes, perhaps abstractions of low-level stimulus features. However, the format of these putative abstract representations has thus far remained impenetrable. Here, we demonstrate that different types of visual stimuli can be flexibly recoded into the same WM format when that representation is useful for memory-guided behavior. Specifically, we found that the patterns of activity in visual cortex during WM for gratings and dot motion, two very different retinal inputs, are interchangeable when participants were later tested on the orientation of the grating or the global direction of the motion. Critically, the behaviorally relevant feature of the stimuli was extracted and recoded into a shared mnemonic representation that takes the form of an abstract line-like pattern within spatial topographic maps.

RESULTS

Working memory representations for orientation and motion direction share a common format

We measured fMRI brain activity while participants used their memory to estimate the orientation of a stored grating or the stored direction of a cloud of moving dots after a 12 s retention interval (Figure 1A). Focusing on patterns of delay period activity, we first demonstrate that we could classify both grating orientation and motion direction in several maps (Figure 1B) along the visual hierarchy (Figures 2A and S1A: delay epoch, within-stimulus), consistent with previous investigations (Emrich et al., 2013; Ester et al., 2015; Harrison and Tong, 2009; Riggall and Postle, 2012; Sarma et al., 2016; Serences et al., 2009; Yu and Shim, 2017). Perhaps, neurons with orientation (Hubel and Wiesel, 1962) or directional motion selectivity (Maunsell and Van Essen, 1983) encode and maintain representations of these aspects of the physical stimuli. Alternatively, the format of these mnemonic representations might reflect efficient abstractions of the image-level properties of the stimuli. For instance, memory may take the form of a compressed, low-resolution summary of the global direction of thousands of dots moving over time akin to a line-like pointer.

Figure 1. Neuroimaging experiments.

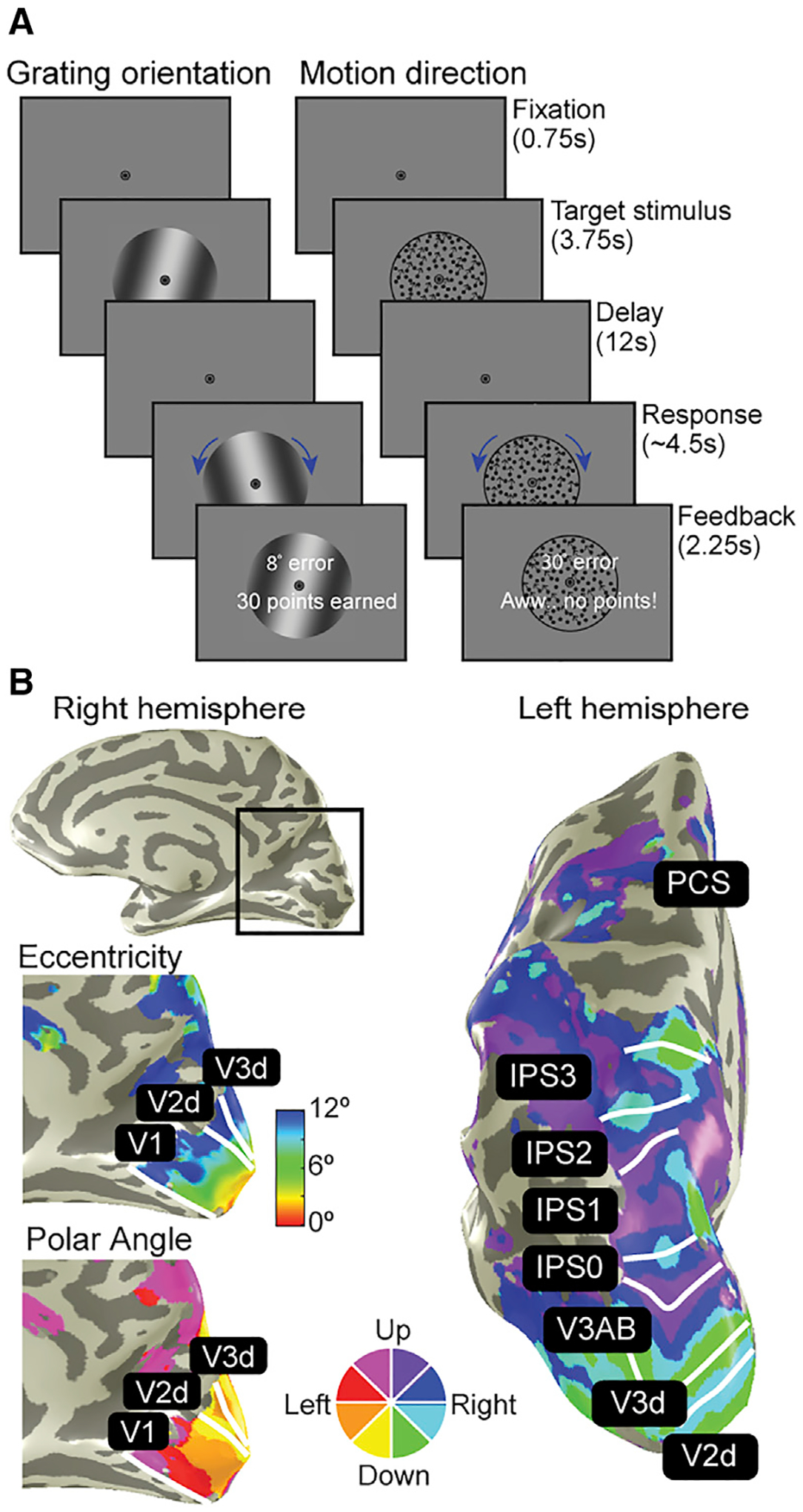
(A) Working memory experiments. Participants maintained the orientation of gratings or the direction of dot motion over a 12 s retention interval. After the delay, participants rotated a recall probe to match their memory, and more points were awarded for more accurate memories.

(B) Population receptive field (pRF) mapping. A separate retinotopic mapping session was used to estimate voxel receptive field parameters for defining visual field maps in occipital, parietal, and frontal cortices. Example participant’s right and left hemispheres are shown.

Figure 2. Working memory representations for orientation and motion direction share a common format.

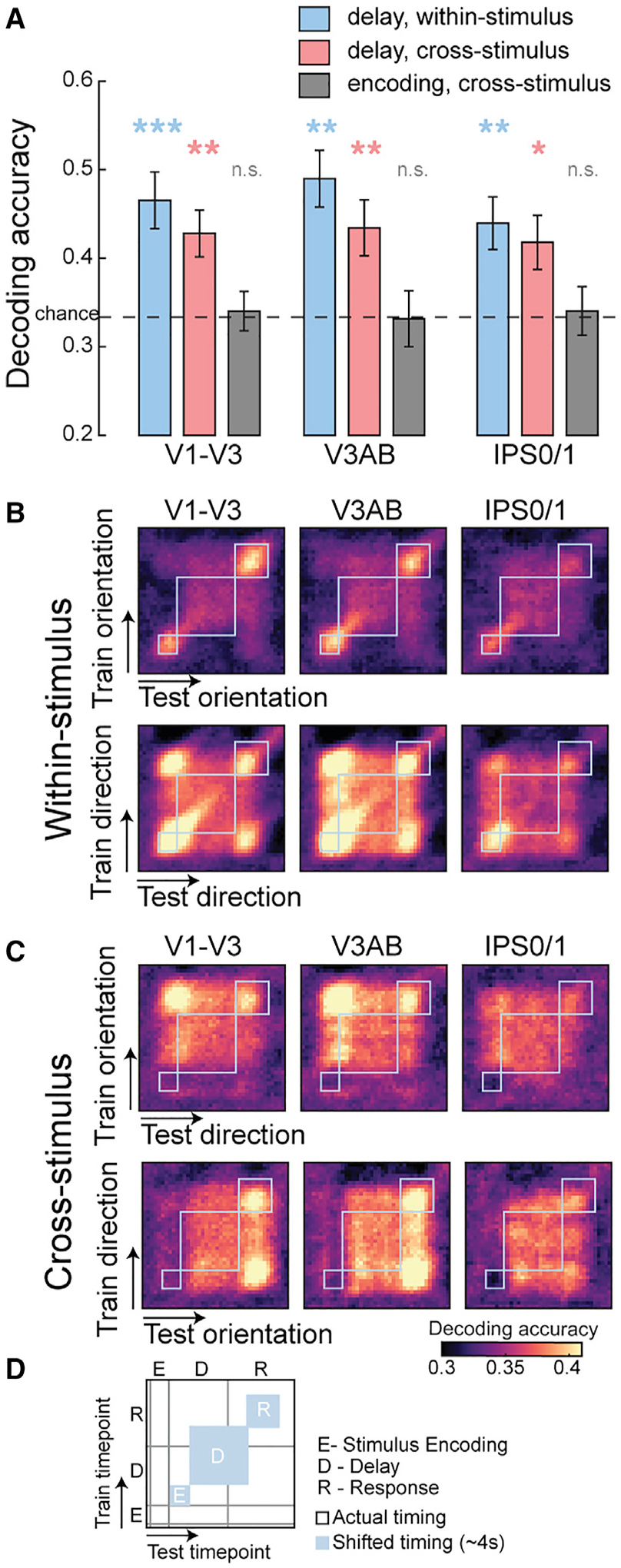
(A) Both remembered grating orientation and dot motion direction could be decoded from the pattern of neural activity during the memory delay (blue bars). We successfully decoded not only within but across stimulus types (e.g., training on orientation can decode motion direction; red bars), indicating that the shared patterns do not represent low-level perceptual details of each stimulus type. Moreover, no such cross-stimulus decoding existed during the stimulus encoding epoch (gray bars). *p < 0.05, **p < 0.01, ***p < 0.001, n.s. not significant, corrected (p values in Table S1). Error bars represent ±1 SEM.

(B and C) Temporal generalization matrix. To evaluate how representations evolve over the time course of a trial, we trained and tested on all possible combinations of time points. Abstract WM codes are stable throughout the delay period. See Figure S1 for other ROIs.

(D) Schematics of the matrix plots. Gray lines denote the actual timing of events, and blue boxes show each of these events shifted by ~4 s assuming hemodynamic lag.

From this hypothesis, we predict a similar pattern of delay period activity when abstract WM formats match despite entirely distinct perceptual inputs. In several cortical regions, a classifier trained on one type of stimulus (e.g., orientation) successfully decoded the other type of stimulus (e.g., direction) when angles matched (Figures 2A and S1A: delay epoch, cross-stimulus). Critically, evidence for an abstract WM representation that was shared across stimulus types was limited to the memory delay period. The lack of cross-stimulus decoding during the time epoch corresponding to direct viewing of the stimulus (Figures 2A and S1A: stimulus encoding epoch, cross-stimulus) indicates that the abstract format is specifically mnemonic in nature and not an artifact inherited from some shared perceptual feature during encoding. Neither can it be attributed to gaze instability as we ruled out eye movements as the potential source of significant decoding (see STAR Methods for details). In the temporal generalization matrix using continuous decoding (King and Dehaene, 2014), one can clearly see the emergence and stability of the abstract WM code during the delay period (Figures 2B, 2C, S1B, and S1C).

Format of recoded working memory representations unveiled

Although our evidence supported a WM representation that is abstract in format, we aimed to reveal the latent nature of the WM representation. We hypothesized that participants recoded the sinusoidal gratings and dot motion kinematograms into line-like images at angles matching the orientation and direction, respectively, of the stimuli. We reasoned that the abstract representation might be encoded spatially in the population activity of topographically organized visual field maps. Specifically, we predicted that the spatial distribution of higher response amplitudes across a topographic map forms a line at a given angle, as if the retinal positions constituting a line were actually visually stimulated.

To test this, we reconstructed the spatial profile of neural activity (Kok and de Lange, 2014; Yoo et al., 2022) during WM by projecting the amplitudes of voxel activity during the delay period for each orientation and direction condition into visual field space (Figure 3A) using parameters obtained from models of each map’s population receptive field (pRF). Using the following equation, we computed the sum (S) of all voxels’ receptive fields (the exponent, which is a Gaussian) weighted by their delay period beta coefficients (β) for each feature condition (θ_i), where i and n are indices of voxels and feature conditions, respectively; x_n, y_n, and σ are the center and width of the pRF; x₀ and y₀ are the positions in the reconstruction map at which the pRFs were evaluated:

$$S_{{\theta }_i}=\sum _{n=1}^N{\beta }_{i,n}\times e^{-\frac{{\left(x_n-x_0\right)}^2+{\left(y_n-y_0\right)}^2}{{\sigma }^2}}$$ (Equation 1)

Figure 3. Unveiling the recoded formats of working memory representations for orientation and motion direction.

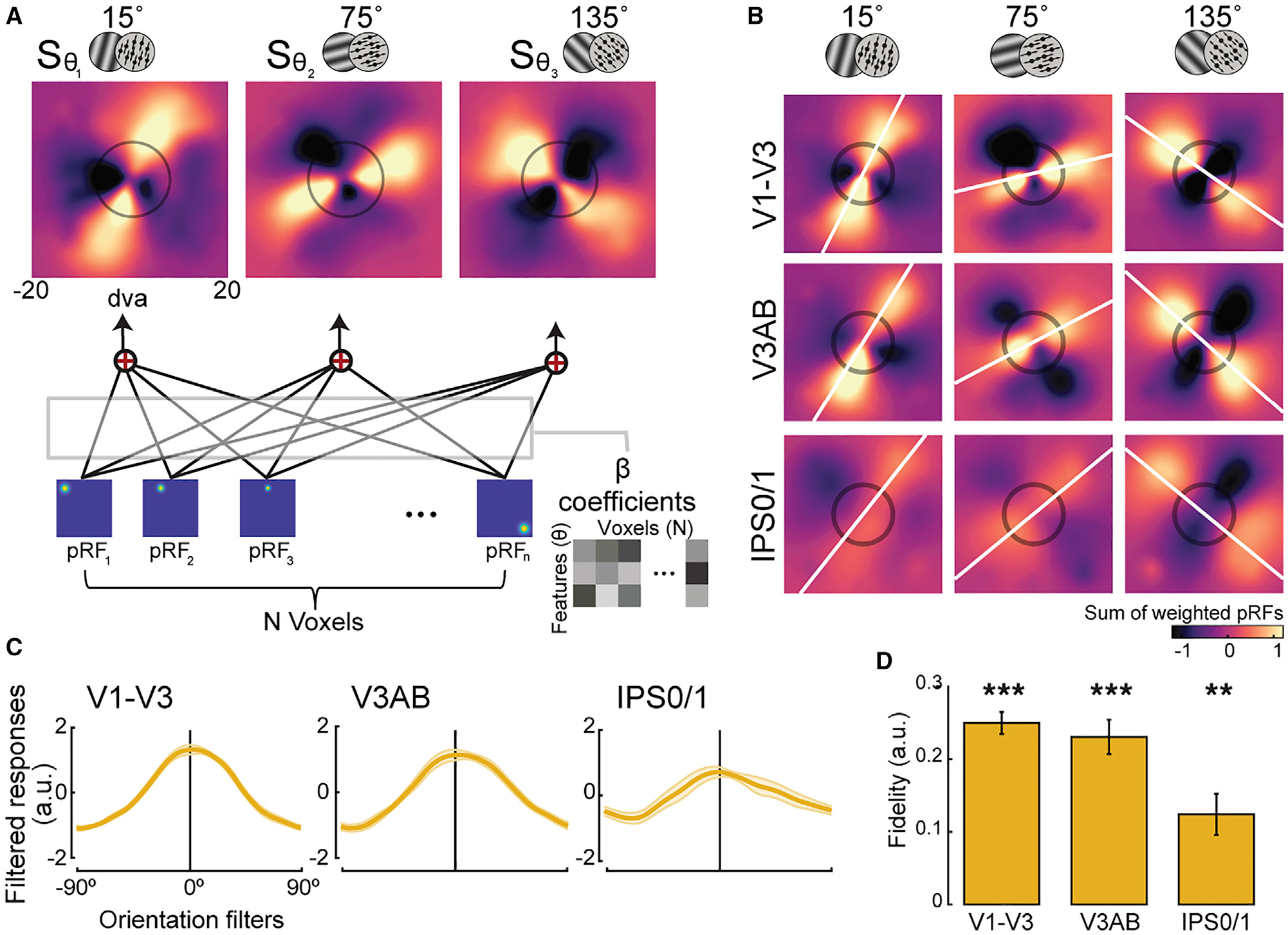
(A) Spatial reconstruction analysis schematics. Voxel activity for each feature condition (orientation/direction; θ) was projected onto visual field space (dva, degrees of visual angle) by computing the sum (S) of voxels’ pRFs weighted by their response amplitudes during the memory delay (β) (see Equation 1; STAR Methods for details).

(B) Population reconstruction maps. Lines across visual space matching the remembered angles of the stimuli emerged from the amplitudes of topographic voxel activity. Best fitting lines (white lines) and the size of the stimulus presented during the encoding epoch (black circles) are shown. See Figure S2 for other ROIs. (C and D) To quantify the amount of remembered information consistent with the true feature, we computed filtered responses and associated fidelity values from the maps in (B). Filtered responses represent the sum of pixel values within the area of a line-shaped mask oriented −90° to 90° (0° represents the true feature), and fidelity values are the result of projecting the filtered responses to 0° (STAR Methods). Higher fidelity values indicate stronger representation. **p < 0.01, ***p < 0.001, corrected (p values in Table S1). Error bars represent ±1 SEM.

Remarkably, the visualization technique confirmed our hypothesis and unveiled a stripe encoded in the amplitudes of voxel activity at an angle matching the remembered feature in many of the visual maps (Figures 3B and S2A). This evidence strongly suggests that the neural representation of orientation/direction in memory is similar to that which would be evoked by retinal stimulation of a simple-line stimulus. Interestingly, these line-like representations had greater activation at the end of the line corresponding to the direction of motion, akin to an arrowhead, perhaps allowing for both the storage of the angle and direction of motion (Figure S4B).

To quantify the extent to which the angled stripes in the reconstructed maps aligned with the actual orientation/direction of the stimuli, we computed filtered responses and associated fidelity values (Figures 3C, 3D, S2B, and S2C). The significant fidelity values (Figure 3D) indicate that the mechanism by which orientation and motion direction is stored in WM depends on a spatial recoding into the population’s topography. We found the same pattern of results when reconstructing the maps for orientation and motion direction trials separately (Figures S2D–S2G), when controlling for potential biases in pRF structure across the visual field, and when reconstructing the neural representation with the weight matrices used to classify orientation and motion direction instead of the magnitude of delay period activity. Therefore, the recoded abstract representations we discovered are robust. In summary, neural representations of gratings and dot motion, despite distinct retinal stimulation with distinct neural encoding mechanisms for perception (Cynader and Chernenko, 1976; He et al., 1998), were recoded in memory into a spatial topographic format that was line-like in nature with angles matching the remembered orientation/direction.

Distinct formats of perceptual and mnemonic representations

Next, we used an image-computable model based on properties of V1 (Roth et al., 2018; Simoncelli et al., 1992) to simulate a potential neural mechanism of the line-like patterns (Figures 4 and S3). The topographic pattern of simulated voxel activity when model inputs were simple-line images (Figure 4, bottom row) closely resembled the line-like patterns that we observed in our experimental data in Figure 3B, further strengthening a putative mechanism involving the maintenance of an imagined line in WM. Critically, using the gratings from our experiment as inputs to the model, the reconstructed maps produced line patterns orthogonal to those observed experimentally (Figure 4, top row). Such orthogonality for grating images is likely due to aperture bias during perception reported previously, where orientation preference of voxels in the early visual cortex is affected by spatial biases induced by stimulus aperture (Freeman et al., 2011; Roth et al., 2018). The dissociation between the simulated reconstructions of gratings and lines demonstrates that the format of the WM representations resembles that of a low-dimensional line rather than a high-resolution pixel-by-pixel image of a grating (Figure S3B). Therefore, based on the V1 model, we demonstrated the feasibility of a line-like WM representation. The model also helped rule out potential confounds specific to visual cortex, confounds that are unlikely to apply to parietal cortex. Furthermore, although the model does not simulate the effects of motion, we found striking evidence from our experimental data that the line-like representations during WM for motion are distinct from those during perception (Figure S4).

Figure 4. Model simulation for orientation: distinct formats for perceptual and mnemonic representations.

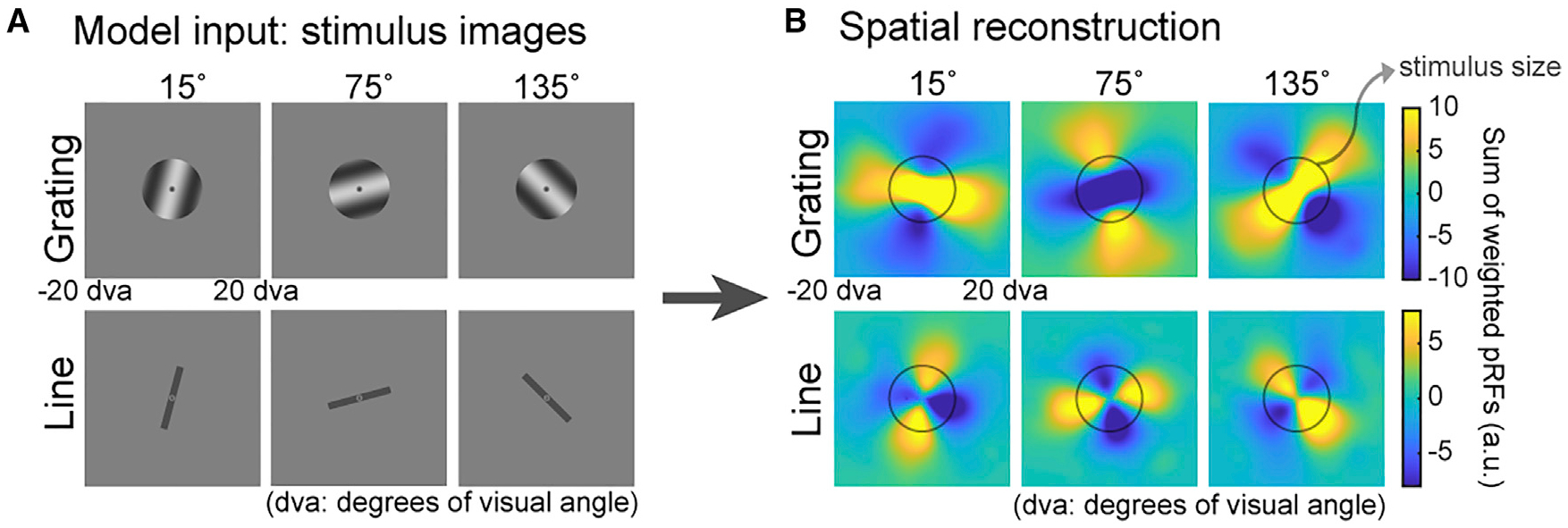
(A) Gratings identical to the ones used in the experiment and lines oriented at 15°, 75°, and 135° clockwise from vertical were fed into an image-computable model of V1 to simulate the population response.

(B) We repeated the spatial reconstruction analysis in Figure 3A with simulated V1 voxel amplitudes acquired through sampling the model output neuronal responses (Figure S3A) with pRF parameters (STAR Methods). The simulated topographic patterns when model inputs are lines, but not gratings, closely match our experiment data (Figure 3B), suggesting that mnemonic representations of oriented gratings are similar to perceptual representations of simple line.

DISCUSSION

Together, these results directly impact key tenets of the sensory recruitment theory of WM, which proposes that the same neural mechanisms that encode stimulus features in sensory cortex during perception are recruited by higher-level control areas such as prefrontal and parietal cortices to support memory (Curtis and D’Esposito, 2003; Postle, 2006; Serences, 2016). First, our findings indicate that the mechanisms by which WM and perception are encoded in visual cortex can differ in certain circumstances. The recoding of gratings and dot motion into line-like WM representations explains why previous studies have reported null or weaker effects—brain activation patterns during perception of a stimulus are poor predictors of patterns during WM, especially when compared with training on patterns during WM (Albers et al., 2013; Hallenbeck et al., 2021; Rademaker et al., 2019; Serences et al., 2009; Spaak et al., 2017). Although WM representations may contain some sensory-like information, our results provide robust evidence that perceptual information can be reformatted for memory storage. Second, the spatial nature of the recoded WM representation offers intriguing insights into how the parietal cortex, which lacks neurons with clear orientation or motion directional tuning (Kusunoki et al., 2000), supports WM. Recoding into a spatial format may exploit the prevalent spatial representations in parietal cortex (Heilman et al., 1985; Mackey et al., 2016, 2017) and explain why previous studies have been able to decode features such as orientation from patterns in parietal cortex (Bettencourt and Xu, 2016; Ester et al., 2015; Rademaker et al., 2019; Yu and Shim, 2017). In addition to serving as a mechanism for WM storage, this spatial code in parietal cortex might conceivably reflect the origins of top-down feedback. Indeed, WM representations in visual cortex are thought to depend on feedback signals (van Kerkoerle et al., 2017; Rahmati et al., 2018). This may be why we found the line-like spatial code in the early visual cortex despite the abundance of neurons tuned for orientation and motion (Hubel and Wiesel, 1962; Maunsell and Van Essen, 1983). Perhaps, the retinotopic organization shared between visual and parietal cortices forms an interface where the currency of the feedback is simple retinotopic space. Alternatively, a more complicated feedback mechanism may exist that specifically targets neurons that are both tuned to the memorized feature and contain overlapping spatial receptive fields. Third, distinct representational formats for perception and memory solves the mystery of how visual cortex can simultaneously represent WM content and process incoming visual information without catastrophic loss (Bettencourt and Xu, 2016; Buschman, 2021; Hallenbeck et al., 2021; Rademaker et al., 2019).

These results also impact how we think about the nature of WM representations, especially when we consider the larger constraints and goals of the memory system. A line is an efficient summary representation of orientation and motion direction compared with the complexity of the sensory stimuli from which it is abstracted and may provide a means to overcome the hallmark capacity limits of WM (Miller, 1956). Compare in bits of information the hundreds of dots displaced each frame over several seconds to a single line pointing in the direction of motion. But why a line? The immediate behavioral goal—the “working” part of WM—may largely determine the nature of the code. Consistent with the idea of WM as a goal-directed mechanism, previous studies have found that only the task-relevant feature, but not those irrelevant to the task, is retained in WM (Serences et al., 2009; Yu and Shim, 2017). Therefore, we note that the current experimental task, in which participants were asked to remember orientation and direction among many other visual properties of the stimuli, could have encouraged the recoding into the spatial line representation, a format most proximal to the specific mnemonic demands of the task. In fact, the flexible nature of WM might lead to different representational formats depending on the stimulus being remembered and the task at hand. Written letters or words are converted from a visual into a phonological or sound-based code when stored in WM (Baddeley, 1992). Prospective motor codes are possible when memory-guided responses can be planned or anticipated (Boettcher et al., 2021; Curtis and D’Esposito, 2006; Curtis et al., 2004). When appropriate, WM representations can take the form of the categories abstracted from perceptual exemplars (Lee et al., 2013). On the other hand, it is likely that memory for a stimulus feature in its simplest form, such as visual location that cannot be simplified any more than its spatial coordinates, does not undergo recoding (Hallenbeck et al., 2021; Li et al., 2021).

The idea that memory representations can take a form other than the perceptual features of the stimulus is not new. Our results are striking, however, because they both clearly establish the existence of abstract WM codes in the visual system and more importantly unveil the nature of these WM representations. Visualizing the abstractions of stimuli in the topographic patterns of brain activity is powerful evidence that visual cortex acts as a blackboard for cognitive representations rather than simply a register for incoming visual information (Roelfsema and de Lange, 2016).

STAR★METHODS

RESOURCE AVAILABILITY

Lead contact

Further information and requests for resources and reagents should be directed to and will be fulfilled by the lead contact, Clayton Curtis (clayton.curtis@nyu.edu).

Materials availability

This study did not produce new materials.

Data and code availability

The processed fMRI data generated in this study have been deposited in the Open Science Framework https://osf.io/t6b95. Processed fMRI data contains extracted beta coefficients from each voxel of each ROI. The raw fMRI data are available under restricted access to ensure participant privacy; access can be obtained by contacting the corresponding authors. All original code for data analysis is publicly available on GitHub https://github.com/clayspacelab and https://github.com/yunakwak as of the date of publication.

EXPERIMENTAL MODEL AND SUBJECT DETAILS

Eleven neurologically healthy volunteers (including the 2 authors; 6 females; 25–50 years old) with normal or corrected-to-normal vision participated in this study. They gave informed consent approved by New York University IRB (protocol IRB-FY2016–852). Each participant completed 2 experimental sessions (~2hrs each) and 1–2 sessions of retinotopic mapping and anatomical scans (~2hrs).

METHOD DETAILS

Experimental stimuli and task

Participants performed a delayed-estimation WM task where they reported the remembered orientation or motion direction. Each trial began with 0.75s of central fixation (subtended 0.7° diameter) followed by the presentation of a target stimulus for 3.75s (presented in donut-shaped circular aperture with 1.5° inner and 15° outer diameter). The stimulus was a drifting grating (contrast = 0.6, spatial frequency = 0.1 cycle/°, phase change = 0.12°/frame) or a random dot kinematogram (RDK; number of dots = 900, size of each dot = 0.12°, speed of each dot = 0.08°/frame, initial coherence = 0.91), presented in blocked designs and in interleaved order. After a 12s delay period, they rotated a recall probe with a dial to match the remembered orientation/direction within a 4.5s response window. The recall probe matched the target stimulus type presented during encoding (e.g., target and recall probe were both gratings for orientation), instead of line bars for example, to prevent from enforcing participants to represent the two stimulus types in an abstract manner. However, there were two exceptions: the recall probe for orientation was a static grating without drifting motion, and the coherence of RDK dots was fixed at 1 throughout the whole response period (see below for adjusting dot coherence level in the stimulus encoding epoch). Participants were provided with feedback on the magnitude of error (°) and the points earned based on the error they made on each trial (40 points for error less than 3°, 30 points for error between 3°−12°, 20 points for error between 12°−21°, 10 points for error between 21°−30°, and no points for error exceeding 30°). The feedback display lasted for 2.25s and was followed by an inter-trial-interval of 7.5s or 9s. All stimuli were presented in a circular aperture spanning the whole visual field.

Data were collected across two sessions for each participant resulting in 22 runs (10 orientation, 12 motion direction) for 8 participants and 21 runs (10 orientation, 11 motion direction) for 3 participants. Each run consisted of 12 trials. For the orientation runs, the target orientations were 15°, 75°, and 135° clockwise from vertical with random jitters (<5°), each repeated 4 times within a run. For motion direction runs, the target directions were 15°, 75°, 135°, 195° (180° apart from 15° and thus opposite in direction from 15°), 255° (180° apart from 75°), and 315° (180° apart from 135°) clockwise from vertical with random jitters (<5°), each repeated 2 times within a run. We collected 1–2 more runs for the motion direction for each participant because we collapsed across the opposite direction trials and labeled them as the same condition for decoding. The orientation/direction of the recall probe was randomized, with the constraint that the direction difference between the target and probe RDKs was less than 90° to match with the orientation trials.

To address the difference in task difficulty across the two stimulus types, dot coherence for the RDK target was staircased. The first trial of each motion direction run began with the coherence of 0.91, and the coherence of the following trials followed a 1-up 2-down staircase method with reference to the performance of the previous orientation run (median of error in trials of the previous orientation run). Although we tried to match the task difficulty across the two stimulus types, performance was significantly lower (t(10)= 2.525, p = 0.023) for the motion direction trials (mean = 9.26°, s.d. = 3.307°) compare to the orientation trials (mean = 7.72°, s.d. = 2.681°).

fMRI data acquisition

BOLD contrast images were acquired using Multiband (MB) 2D GE-EPI (MB factor of 4, 44 slices, 2.5 × 2.5 × 2.5mm voxel size, TE/TR of 30/750ms). We also acquired distortion mapping scans to measure field inhomogeneities with normal and reversed phase encoding using a 2D SE-EPI readout and number of slices matching that of the GE-EPI (TE/TR of 45.6/3537ms). T1- and T2-weighted images were acquired using the Siemens product MPRAGE (192 slices for T1 and 224 slices for T2, 0.8 × 0.8 × 0.8mm voxel size, TE/TR of 2.24/2400ms for T1 and 564/3200ms for T2, 256 × 240 mm FOV). We collected 2–3 T1 images and 1–2 T2 images per participant.

fMRI data preprocessing

We used intensity-normalized high-resolution anatomical scans as input to Freesurfer’s recon-all script (version 6.0) to identify pial and white matter surfaces, which were converted to the SUMA format. This anatomical image processed for each subject was the alignment target for all functional images. For functional preprocessing, we divided each functional session into 2 to 6 sub-sessions consisting of 2 to 5 task runs split by distortion runs (a pair of spin-echo images acquired in opposite phase encoding directions) and applied all preprocessing steps described below to each sub-session independently.

First, we corrected functional images for intensity inhomogeneity induced by the high-density receive coil by dividing all images by a smoothed bias field which was computed by a ratio of signal acquired with the head coil to that of the body coil. Then, to improve co-registration of functional data to the target T1 anatomical image, transformation matrices between functional and anatomical images were computed using distortion-corrected and averaged spin-echo images (distortion scans used to compute distortion fields restricted to the phase-encoding direction). Then we used the distortion-correction procedure in afni_proc.py to undistort and motion-correct functional images. The next step was rendering functional data from native acquisition space into un-warped, motion corrected, and co-registered anatomical space for each participant at the same voxel size as data acquisition (2.5mm iso-tropic voxel). This volume-space data was projected onto the reconstructed cortical surface, which was projected back into the volume space for all analyses.

We linearly detrended activation values from each voxel from each run. These values were then converted to percent signal change by dividing by the mean of the voxel’s activation values over each run.

Regions-of-interest definition

For identifying regions of interest (ROIs) and acquiring voxels’ population receptive field (pRF) parameters (Figure 1B), we collected data from a separate retinotopic mapping session for each participant (8–12 runs). Participants ran in either one of the two types of attention-demanding tasks: RDK motion direction discrimination task (6 participants) (Mackey et al., 2017) or a rapid serial visual presentation (RSVP) task of object images (5 participants).

In each trial of the RDK motion discrimination task, a bar with pseudo-randomly chosen width (2.5°, 5.0°, and 7.5°) and sweep direction (left-to-right, right-to-left, bottom-to-top, top-to-bottom) swept across 26.4° of the visual field in 12 2.6s steps. Each bar was divided into 3 equal-sized patches (left, center, right). In each sweep, the RDK direction in one of the peripheral patches matched that of the central patch, and participants reported which peripheral patch had the same motion direction with the central patch. The coherence of the RDK in the two peripheral patches was fixed at 50%, and the coherence of the RDK in the central patch was adjusted using a 3-down 1-up staircase procedure to maintain 80% accuracy.

In each trial of the object image RSVP task, a bar consisting of 6 different object images (each image subtended 4.6° × 4.6°) swept across 26.4° of the visual field in one of the 4 sweep directions (left-to-right, right-to-left, bottom-to-top, top-to-bottom) in 12 steps. In each sweep, participants reported whether the target object image existed among the 6 images. The target image was pseudo-randomly chosen in each run and was shown at the beginning of each run at 5 locations in the visual field (center, left, right, up, down). Presentation duration of the object images was set to 400ms on the first trial of each run but was adjusted according to the accuracy on the previous trial. Duration increased with accuracy below 70%, decreased with accuracy above 85%, and stayed the same for accuracy values in between.

BOLD contrast images were acquired using MB 2D GE-EPI (MB factor of 4, 56 slices, 2 × 2 × 2mm voxel size, TE/TR: 42/1300ms). Similar to the main experimental scans (see fMRI data preprocessing), we collected distortion mapping scans to measure field inhomogeneities with normal and reversed phase encoding using a 2D SE-EPI readout and number of slices matching that of the GE-EPI (TE/TR: 71.8/6690ms). The same preprocessing steps used for the main experimental data were applied to the retinotopic mapping data with one exception. Because the experimental and retinotopy scans were acquired with different voxel grid resolution, we projected the retinotopy time series data onto the surface from its native space resolution (2mm), then from the surface to volume space at the task voxel resolution (2.5mm) to compute pRF properties in the same voxel grid as the experimental data.

Using the averaged time series across all retinotopy runs for each participant, we fit a pRF model using vistasoft (github.com/clayspacelab/vistasoft; Dumoulin and Wandell, 2008; Mackey et al., 2017). After estimating the pRF parameters for all the voxels, we projected the best-fit polar angle and eccentricity parameters onto each participant’s inflated brain surface map via AFNI and SUMA. ROIs were drawn on the surface based on established criteria for polar angle reversals and foveal representations (Mackey et al., 2017; Wandell et al., 2007), with the variance explained threshold set to ~10%. We defined ROIs V1-V3, V3AB, TO1/2, IPS0/1, IPS2/3, and PCS. We merged ROIs for V1-V3, TO1/2, IPS0/1, IPS2/3, and PCS (sPCS/iPCS) which was justified as the regions being grouped belong to the same cluster defined by overlapping foveal representations (Wandell et al., 2007). For merged ROIs, the voxels were concatenated before multivariate analysis.

fMRI data analysis: Decoding accuracy

All decoding analyses were performed using the multinomial logistic regression with custom code based on the Princeton MVPA toolbox (github.com/princetonuniversity/princeton-mvpa-toolbox) which uses the MATLAB Neural Network Toolbox. ‘Softmax’ and ‘cross entropy’ were used as activation and performance functions. These two functions are reasonable choices for multi-class linear classification problems because they normalize the activation outputs to sum to 1. The scaled conjugate gradient method was used to fit the weights and bias parameters.

Our main analysis was performing decoding on the delay epoch representation. Within-stimulus decoding on the delay epoch was performed by training and testing on the same stimulus type (e.g., training and testing on orientation). Cross-stimulus decoding on the delay epoch was conducted by training and testing on the delay representation of different stimulus types (e.g., training on orientation and testing on motion direction). We were mostly interested in the cross-stimulus decoding results on the delay epoch data as we aimed to examine whether a common representational format existed in WM across different stimulus types with similar nature.

Classification was performed on the beta coefficients acquired from running a voxel-wise general linear model (GLM) using AFNI 3dDeconvolve, on all the runs acquired for each participant. We used GLM to estimate the responses of each voxel to the stimulus encoding, delay, response, feedback, and the inter-trial-interval epochs. Each epoch was modeled by the convolution of a canonical model of the hemodynamic impulse response function with a square wave (boxcar regressor) whose duration was equal to the duration of the corresponding epoch. Importantly, we estimated beta coefficients for every trial independently for the epoch that was of main interest (e.g., delay epoch) in performing a particular decoding analysis. Other epochs were estimated using a common regressor for all trials (Rissman et al., 2004). This method was used to capitalize on the trial-by-trial variability of the main epoch of interest (e.g., delay epoch) and prevent the trial-by-trial variability of other epochs soaking up a large portion of variance which could potentially be explained by the epoch of interest. Six motion regressors were also included in the GLM. Each voxel’s beta coefficients were z-scored across each run independently for decoding.

We performed a 3-way classification to decode 3 target orientations and 3 motion directions. The orientation conditions were 15°, 75°, and 135° clockwise from vertical, and in the motion direction trials, the two opposite direction conditions sharing the same orientation axis were combined (e.g., 15° and 195° combined into 15°). Therefore, there were 3 target conditions for both stimulus types. For within-stimulus decoding, we implemented the leave-one-run-out cross-validation procedure in which one run was left out on each iteration for testing the performance of the classifier and the rest of the runs were used for training. The decoding accuracies were averaged across all the iterations. For cross-stimulus decoding, the classifier was trained on beta coefficients of all trials in one stimulus type and tested on all other trials in the other stimulus type.

For the temporal generalization decoding analysis, we used z-scored percent signal change values for each TR. A 3TR sliding window was used, meaning that the training and the test data were each voxel’s activity values averaged across 3TRs including the TR being trained or tested.

fMRI data analysis: Spatial reconstruction

To visualize neural activity during the delay period, voxel amplitudes for each orientation/direction condition were projected onto the 2D visual field space (Kok and de Lange, 2014). The same GLM beta coefficients (β) extracted for the decoding analysis were averaged across trials for each feature condition and voxel, and were used for weighting the voxels’ pRFs in Equation 1. The reconstructed maps reflect aspects of the pRF structure such as increase in size with eccentricity (Dumoulin and Wandell, 2008; Mackey et al., 2017), resulting in a dumbbell shape of the reconstructed line patterns.

Furthermore, to take into account the potential bias from the individual difference in pRF structure, we generated a pRF normalized version of the reconstruction maps. More specifically, the pRF bias map for each participant was computed by summing up all voxels’ pRFs without any weighting. Then, the original reconstruction maps (Equation 1) were divided by the pRF bias map separately for each participant. With this procedure, we aimed to examine whether the underlying pRF structure influences the reconstruction patterns for the different orientation/direction conditions.

We also repeated the same reconstruction analysis with classifier weights, instead of beta coefficients, to weight the voxel’s pRFs. With the same classification algorithm used for the decoding analysis, we estimated the classifier weights of all voxels for each ROI separately for each participant, using GLM beta coefficients. No trials needed to be held out for cross-validation because the main purpose of this analysis was to train the classifier for weight estimation and not to test its performance. Note that no voxels were left out in the weight estimation step but only for computing the weighted sum of pRFs (eccentricity ≤ 20° of visual angle). As a result, for each participant and ROI, we had a i (number of target orientation/direction conditions) × n (number of voxels in an ROI) weight matrix w. Therefore, Equation 1 was modified as below.

$$S_{{\theta }_i}=\sum _{n=1}^N{w}_{i,n}\times e^{-\frac{{\left(x_n-x_0\right)}^2+{\left(y_n-y_0\right)}^2}{{\sigma }^2}}$$ (Equation 2)

We confirmed that the classifier weights of the voxels had the same spatial structure as the beta coefficients.

For generating all the spatial reconstruction maps, we down-sampled the resolution of the visual field space such that each pixel corresponded to 0.1° of visual angle (10 pixels/°). Only voxels whose pRF eccentricities were within 20° of visual angle were included in the reconstruction.

To better visualize the line format (white lines in Figure 3B), we fit a first-degree polynomial to the X and Y coordinates of the selected pixels with top 10% image intensity, with the constraint that the fitted polynomial passed through the center. To take into account the difference in magnitude of the image intensity of the selected pixels, we conducted a weighted fit with the weight entry for each pixel corresponding to its rank in terms of image intensity.

Model simulation: Image-computable model of V1

We used the image-computable model to both simulate a putative neural mechanism of maintaining a line in WM, and to rule out the alternative account that the reconstructed lines were caused not by line-like WM representations but by topographic biases in orientation tuning. Previous studies have reported that during perception of oriented gratings, orientation decoding in V1 may depend on a coarse-scale topographic relationship between a voxel’s preference for a spatial angle relative to fixation (e.g., 45°, up and to the right) and the matching orientation of the grating (e.g., tilted 45° clockwise from vertical), as well as biases induced by the apertures bounding the stimulus grating (Freeman et al., 2011; Roth et al., 2018). For example, a neuron may exhibit ostensible orientation tuning because of its receptive field overlapping with stimulus edge or change in contrast due to aperture. A neuron may even be orientation-selective, but its orientation selectivity could change depending on stimulus aperture. Therefore, we aimed to compare the model simulation results to gratings used in the present experiment and simple line images (Figure 4).

The image-computable model is based on the steerable pyramid, a subband image transform that decomposes an image into spatial frequency and orientation channels (Roth et al., 2018; Simoncelli et al., 1992). Responses of many linear receptive fields (RFs) are simulated, each of which computes a weighted sum of the stimulus image. The weights determine the spatial frequency and orientation tuning of the linear RFs, which are hypothetical basis sets of spatial frequency and orientation tuning curves of V1. For the model simulation, we used 16 subbands comprised of 4 spatial frequency bands (spatial frequency bandwidth = 0.5 octave) and 4 orientation bands (orientation bandwidth = 90°), which were parameters that could be chosen flexibly. The number of the spatial frequency bands is determined by the size of the stimulus image and the spatial frequency bandwidth parameter. Also, using more than 4 orientation bands (e.g., 6 orientation bands; bandwidth = 60°) corresponding to narrower tuning curves did not change the results.

The inputs to the model were our 1280 × 1024 stimulus images: grating or line images oriented 15°, 75°, 135° clockwise from vertical (Figure 4A; images are shown square for the purpose of illustration to match with the spatial reconstruction maps). Only for the grating images there were 15 phases evenly distributed between 0 and 2 π. The input images had the same configuration as the stimuli in the actual experiment (size of fixation, inner aperture, outer aperture, etc), and the outputs of the model were images of the same resolution as the input images. Each pixel of the output image corresponded to the simulated neuron in the retinotopic map of V1. We first measured the model’s responses to each stimulus image separately. Then, for the grating images, we averaged across the model responses to 15 different phases for each orientation condition. As a result, we had 3 (number of orientation conditions) neuronal response output images for 16 different subbands. For model outputs to grating images, we present the sum of two subbands whose center spatial frequencies are closest to the spatial frequency of the grating stimulus, one of which is the subband with the maximal response (Figures 4 and S3A). This is a reasonable choice because the grating is a narrow-band stimulus. For model outputs to line images, we present the sum of all subbands instead (Figures 4 and S3A). For completeness, the sum of all subbands for the grating images and the subband with the maximal response for line images are shown in Figures S3C and S3D.

To simulate voxel-level responses based on the model outputs, we conducted a pRF sampling analysis (Roth et al., 2018). For each subband and orientation condition, each participant’s pRF gaussian parameters of V1 voxels were used to weigh the model outputs, computing a weighted sum of neuronal responses corresponding to the voxels’ pRFs. This sampling procedure resulted in one simulated beta coefficient for each voxel. Therefore, we generated 3 (number of orientation conditions) × N (number of voxel) beta coefficients for each subband and participant, separately for the grating and line images. We pushed these simulated beta coefficients into the same spatial reconstruction analysis in Figure 3A after z-scoring.

Eye tracking analysis and results

Eye positions were monitored throughout the entire experiment to ensure that participants maintained fixation particularly during the delay epoch. 95.74% of the total number of eye position sample points in the delay epoch across all participants were within 2° eccentricity from the center (the fixation and the stimulus subtended 0.7° and 15° diameter, respectively). Circular correlation between the polar angle of the target orientation/direction and the polar angle of the eye coordinates suggest that the polar angle of the stimulus was not predictive of eye movements (mean = 0.03, s.d. = 0.080, t (10) = 1.24, p = 0.118).

Apparatus

All stimuli were generated via PsychToolBox (Brainard, 1997) in Matlab 2018a and presented via ViewPixx PRoPixx projector (screen resolution: 1280 ×1024 for experimental task and RDK retinotopic mapping task, 1080 × 1080 for object image retinotopic mapping task; refresh rate: 60Hz for all tasks). The viewing distance was 63cm, and the projected image spanned 36.1cm height and 45.1cm width. All functional MRI images were acquired at the NYU Center for Brain Imaging 3T Siemens Prisma Scanner with the Siemens 64 channel head/neck coil. Eye tracking data were acquired using an MR-compatible Eye link 1000 infrared eye tracker (SR Research). X, Y coordinates of the eye positions were recorded at 500 or 1000 Hz.

Glitches

For S02, S03, and S07, fMRI data from one of the 22 experimental task runs was not saved due to the computer freezing at the end of the runs. Eye tracking data for one of the experimental task runs was lost for S02 and S08 due to file corruption. Eye positions were not monitored for S07 during one of the two experimental task sessions due to technical issues, and in the session in which eye positions were recorded, eye data for one of the runs was lost due to file corruption.

QUANTIFICATION AND STATISTICAL PROCEDURES

The statistical results reported here are all based on permutation testing over 1000 iterations with shuffled data (see Table S1). P values reflect the proportion of a metric (F scores, t scores, reconstruction fidelity) in the permuted null distribution greater than or equal to the metric computed using intact data. Note that the minimum p value achievable with this procedure is 0.001. P values were FDR corrected when applicable (Benjamini and Hochberg, 1995).

For statistical testing of fMRI decoding accuracy, we generated permuted null distributions of decoding accuracy values for each epoch (delay/stimulus encoding), decoding type (cross/within), stimulus type (orientation/direction), ROI, and participant. On each iteration, we shuffled the training data matrix (voxels × trials) across both dimensions so that both voxel information and orientation/direction labels could be shuffled. This procedure was conducted for each of the 11 participants resulting in 11 null decoding accuracy estimates per one iteration of permutation. Depending on the statistical tests being performed, we calculated null t scores or F values for each iteration of permutation.

For the spatial reconstruction analysis, we computed reconstruction fidelity to quantify the amount of remembered orientation/direction feature information present in the reconstruction maps (Hallenbeck et al., 2021; Rademaker et al., 2019). Line filters with orientations evenly spaced between −90° and 90° in steps of 1° were used to sum up pixels of the z-scored reconstruction maps within the masked area of the maps. More specifically, a line filter oriented θ° includes pixels with coordinates that form an acute angle to θ° (dot product > 0) and that have a projected distance squared less than 1000. Using different width parameters (projected distance squared) of the orientation filters did not change the results. For each participant, feature condition, and ROI, we generated a tuning curve-like function where x-axis and y-axis represent the orientation of each line filter and the z-scored sum of pixel values masked by the filters, respectively. The filtered responses for each condition were aligned to the true orientation/direction (0°) and then averaged. To compute fidelity, we projected the filtered responses at each orientation filter onto a vector centered on the true orientation (0°) and took the mean of all the projected vectors. Conceptually, this metric measures whether and how strongly the reconstruction on average points in the correct direction. The real fidelity value was compared against the distribution of null fidelity values from shuffled data. To generate the null distribution, the matrix of beta coefficients was shuffled across both the voxel and orientation/direction condition label dimensions, and the shuffled beta coefficients were used to weight the voxels’ pRF parameters. The same logic applied to calculating reconstruction fidelity from direction filters, with the exception that the filters were evenly spaced between −90° and 270° in steps of 1° and the filtered responses were aligned so that the true direction peaked at 90° and 180°.

KEY RESOURCES TABLE

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Deposited data
fMRI data	This paper	https://osf.io/t6b95/(https://doi.org/10.17605/OSF.IO/T6B95)
Software and algorithms
MATLAB	MathWorks	https://www.mathworks.com/products/matlab.html
Custom code and algorithm	This paper	https://github.com/yuna.kwak and https://github.com/clayspacelab (https://doi.org/10.5281/zenodo.6342189)
Image-computable model of V1	Roth et al. (2018)	https://github.com/elifesciences-publications/stimulusVignetting
Decoding	Princeton MVPA toolbox	https://github.com/princetonuniversity/princeton-mvpa-toolbox

Highlights.

• We revealed the neural nature of abstract WM representations

• Distinct visual stimuli were recoded into a shared abstract memory format

• Memory formats for orientation and motion direction were recoded into a line-like pattern

• Such formats are more efficient and proximal to the behaviors they guide