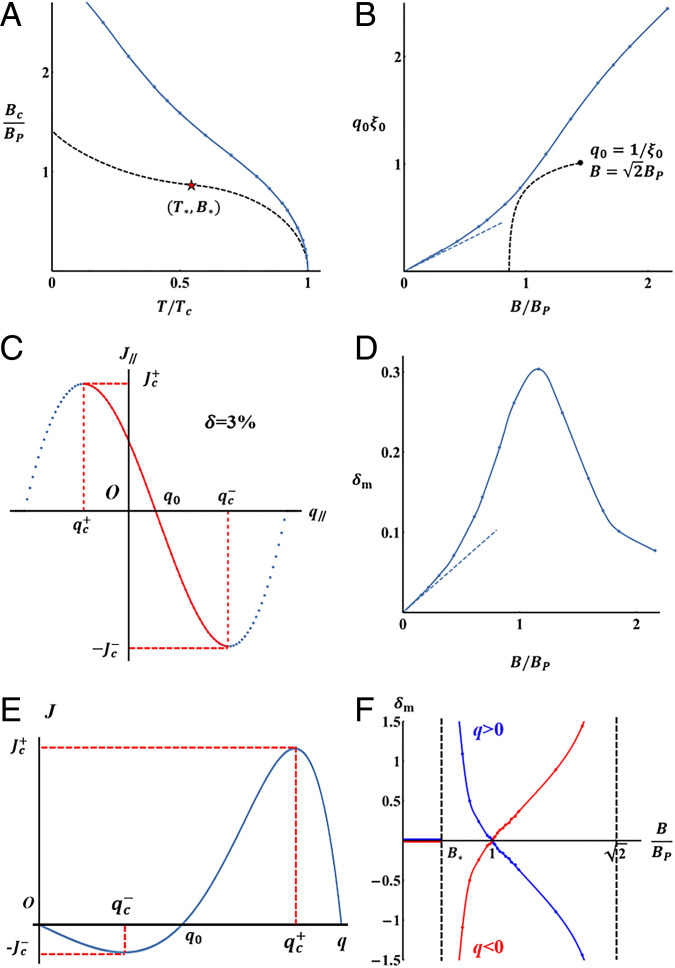
Fig. 3.

(A) In-plane critical field $B_c(T)$ as a function of temperature, for superconductors without SOC (dashed black line) and with Rashba SOC (blue line), where T_c is the zero-field critical temperature, and $B_P=1.25T_c$ is the Pauli limit. In the BCS case, the red star denotes the tricritical point of FFLO transition. In the Rashba superconductor, ${\alpha }_{\text{R}}=0.2v_{\text{F}},{\mathrm{\Delta }}_{so}=2{\mathrm{\Delta }}_0$, and ${\mathrm{\Delta }}_0=1.76T_c$ is the zero-temperature order parameter at zero field. (B) Along the curve $B_c(T)$ in A, field dependence of Cooper pair momentum magnitude q₀, where ${\xi }_0=v_{\text{F}}/{\mathrm{\Delta }}_0$ is the zero-temperature coherence length. Dashed blue line denotes Eq. 18 at weak fields. Dashed black line denotes the BCS case, whose maximum Cooper pair momentum is $q_0={\xi }_0^{-1}$ when $B=\sqrt{2}{B}_P$. (C) Supercurrent $\mathit{J}=J_{\parallel }{\widehat{\mathit{q}}}_0$ as a function of $\mathit{q}=q_{\parallel }{\widehat{\mathit{q}}}_0$ at $T=0.90T_c,B=0.31B_P$. Under external current, red solid line denotes stable states, and blue dots denote unstable states. (D) Along the curve $B_c(T)$ in A, field dependence of ${\delta }_{\text{m}}$ defined in Eq. 23. Dashed blue line denotes Eq. 19 at weak fields. (E) J versus q in a superconductor without SOC in the FF state (q > 0). (F) Along the dashed black curve $B_c(T)$ in A, ${\delta }_{\text{m}}$ as a function of B in a superconductor without SOC. When $B<B_{*}$, δ = 0, and, near B = B_P, there is a sign change of δ. Blue and red colors denote two types of FF states (q > 0 and q < 0).