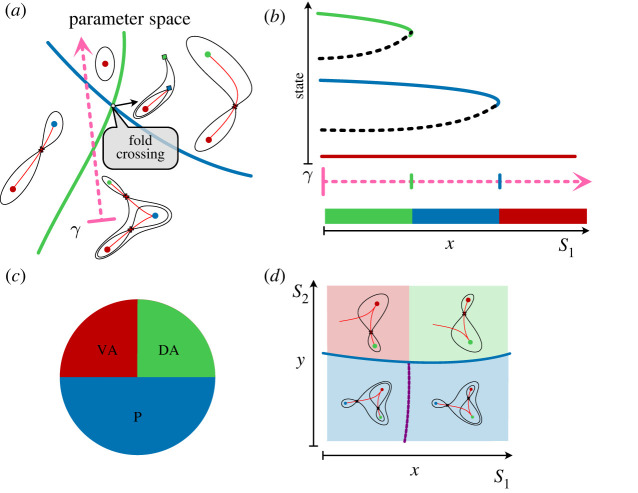
Figure 9.
Fold crossing points of bifurcation curves. (a) Bifurcation set. Landscapes around a fold crossing, corresponding to two adjacent attractors, one central (blue), the others peripheral (green, red). The solid lines represent the bifurcation set with the colour of the line corresponding to the bifurcating attractor. (b) French flag model. The path γ in the 2D parameter space in (a) produces the bifurcation diagram shown in (b). Suppose that the cells are spatially organized in 1D with coordinate x and all cells start in the green attractor. Cells are exposed to a signal S(x) which increases monotonically with x. If x is small so that the signal is small, cells will stay in the green attractor. For larger values of x which will have higher values of the signal, the cells will transition to the blue or red attractor. Moreover, cells will stay in the attractor when the signal decreases. Since the signal is a monotonic function of x this results in a French flag pattern. (c,d) Meinhardt boundary model. When there are two signals, a landscape with a flip curve endpoint as in (d) can produce patterning in a similar fashion. In such an arrangement, a system transitions between three states in response to a combination of two signals. In this model the physical space of the tissue is 2D: one dimension, x, has a gradient of signal S1 and the other, y, has a graded signal S2. All cells are assumed to start in the blue attractor. If signal S2 is small enough that the point (x, y) is below the blue fold curve of the bifurcation set, then the cell stays in this attractor. If (x, y) is above the fold curve this attractor is destroyed in a fold bifurcation and the cells transition to one of the other attractors. Because of the flip, when (x, y) is in the red region (respectively, green region) the state transition to the red (respectively, green) attractor. Moreover, all cells stay in the respective attractor when the signal S2 decreases. Consequently, after a pulse of the signals the spatial patterning is as shown in (c) with three distinct regions of tissue.