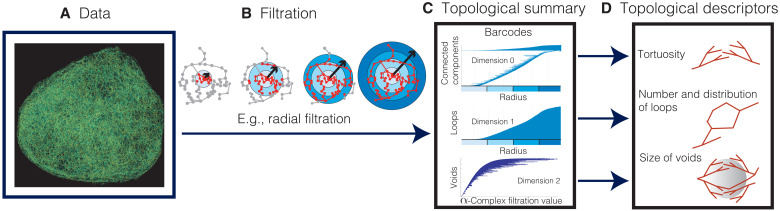
Fig. 3. Schematic illustration of TDA for vascular network data.

(A) We reconstruct the 3D vascular network from image stacks. (B) We apply the radial filtration and the α-complex filtration. (C) We compute the topological summary of the data, which consists of a collection of barcodes (49). The horizontal axis of a barcode represents a spatial parameter such as radial distance to the tumor center (radial filtration) or the scale at which we view the data (α-complex filtration). Every line in a barcode corresponds to a topological feature—i.e., a connected component, loop, or void—in the data. In the radial filtration, we analyze the network within the sphere (highlighted in red) and compute connected components and loops as the sphere grows from the tumor center outward. In the barcodes, the bars start at the radius (measured from the tumor center) where the corresponding connected component or loop first enters the sphere. For a connected component, its corresponding bar ends at the radius at which it merges with another component, i.e., it connects to another part of the vascular network within the growing sphere. A bar representing a loop finishes at the final radius of the filtration. For voids, we study the data at different scales using the α-complex filtration (see the “Topological data analysis” section in Materials and Methods), and the range of a bar represents the scale values where the void is detectable. Its length is a proxy for the volume of the void. (D) We extract interpretable topological descriptors of the data from barcodes.