Figure - PMC

Skip to main content

An official website of the United States government

Here's how you know

Here's how you know

Official websites use .gov
A .gov website belongs to an official government organization in the United States.

Secure .gov websites use HTTPS
A lock ( ) or https:// means you've safely connected to the .gov website. Share sensitive information only on official, secure websites.

View full-text article in PMC

. 2022 Jun 11;85(3):318–321. doi: 10.1016/j.jinf.2022.06.006

Search in PMC
Search in PubMed
View in NLM Catalog
Add to search

© 2022 The Author(s). Published by Elsevier Ltd on behalf of The British Infection Association.

Since January 2020 Elsevier has created a COVID-19 resource centre with free information in English and Mandarin on the novel coronavirus COVID-19. The COVID-19 resource centre is hosted on Elsevier Connect, the company's public news and information website. Elsevier hereby grants permission to make all its COVID-19-related research that is available on the COVID-19 resource centre - including this research content - immediately available in PubMed Central and other publicly funded repositories, such as the WHO COVID database with rights for unrestricted research re-use and analyses in any form or by any means with acknowledgement of the original source. These permissions are granted for free by Elsevier for as long as the COVID-19 resource centre remains active.

PMC Copyright notice

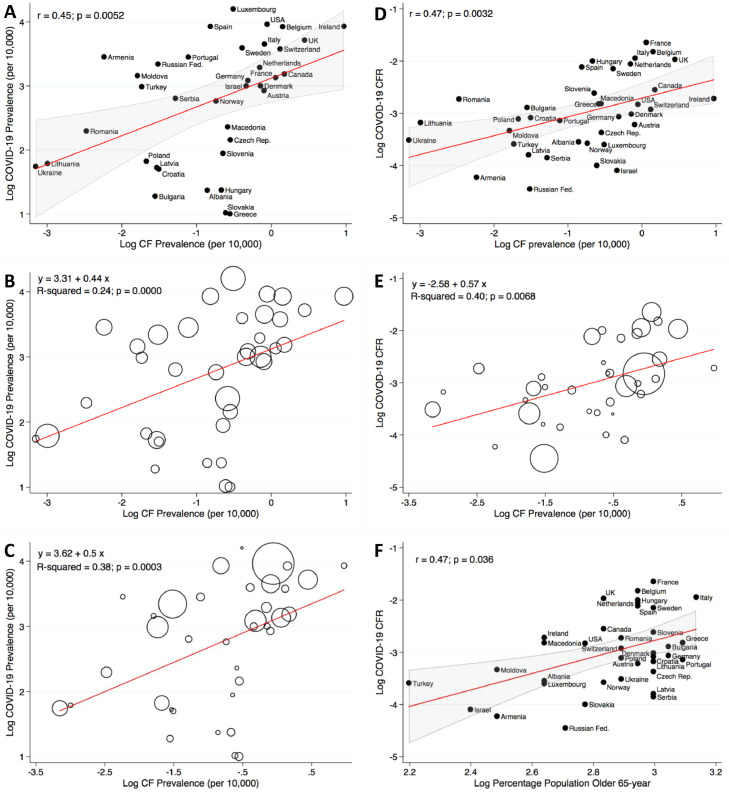
Fig 1 — CF Prevalence Correlation with COVID-19 Prevalence and CFR. Panel A shows a scatterplot with line of best fit (red) and the 95% confidence interval (gray), illustrating a significant direct Pearson's correlation between the prevalence of CF and COVID-19 prevalence in 37 countries. r = 0.45, p = 0.0052. In panel B the liner regression model is weighted for the number of tests performed per 1000 inhabitants in each country. A positive linear correlation between CF and COVID-19 prevalences is confirmed (R²=0.24; p = 0.0000). The size of the marker represents the number of tests performed per 1000 inhabitants. Panel C illustrates a linear regression model weighted for the countries’ inhabitants. A positive correlation between CF and COVID-19 prevalences is seen (R² = 0.38; p = 0.0003). The size of the marker represents the number of inhabitants in each country. Panel D shows a scatterplot with line of best fit (red) and the 95% confidence interval (gray), illustrating a significant direct Pearson's correlation between the prevalence of CF and the COVID-19 CFR. r = 0.47, p = 0.0032. Panel E illustrates a liner regression model weighted for the countries’ inhabitants. A positive correlation between CF prevalence and COVID-19 CFR is seen (R² = 0.40; p = 0.0068). The size of the marker represents the number of inhabitants in each country. In panel F is a scatterplot with line of best fit (red) and the 95% confidence interval (gray), illustrating a significant direct Pearson's correlation between COVID-19 CFR and the percentage of inhabitants older than 65-year. r = 0.47, p = 0.036. Prevalence is expressed per 10,000 inhabitants and all data are in logarithmic scale.