FIGURE 2.

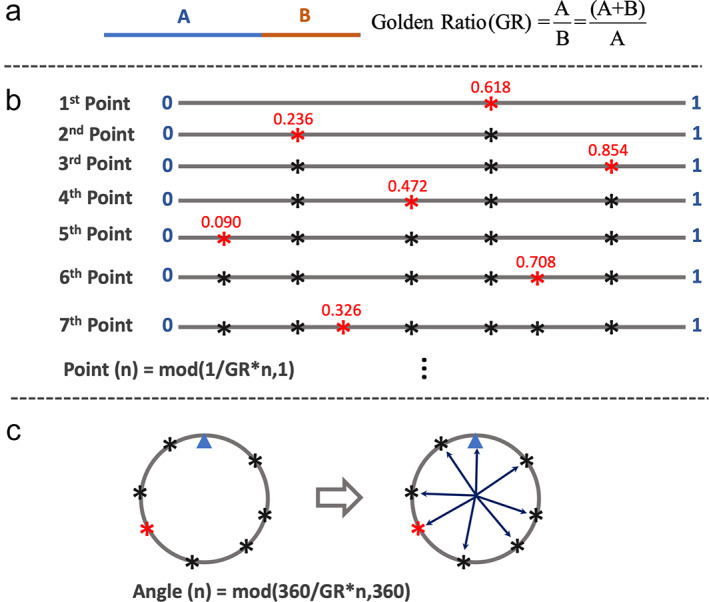
(a) In a line with two segments, the ratio of A and B ($A/B$) is defined as the golden ratio when $A/B=(A+B)/A=1+B/A$. This ratio ≈1.618. (b) A line with the length of 1 is successively divided into smaller segments by the golden ratio. The position of the nth point can be expressed as $\mathrm{mod}\left(\left(1/\mathrm{GR}\right)\times n,1\right)$. It can be seen that each new point always cut the largest segment of the line by the golden ratio, and the points have a roughly uniform distribution on the line. (c) When the seventh line in (b) is bended to connect as a circle, these points also have a roughly uniform distribution on the circle. The small blue triangle in (c) indicates the location where the start and the end positions of the line are connected. The angle of each point can then be calculated as $\mathrm{mod}\left(\left(360/\mathrm{GR}\right)\times n,360\right)$, and the golden angle is ~137.51°.