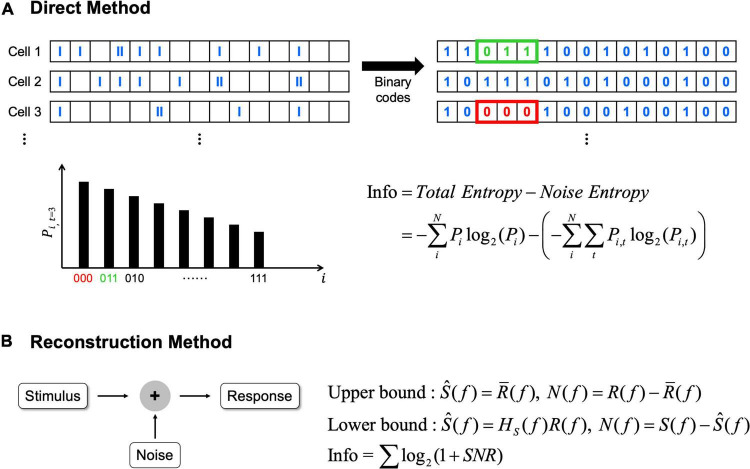
FIGURE 2.

The direct method and the reconstruction method can be applied to calculate information rates. (A) In the direct method, average information rates are the difference between total entropy and noise entropy. N represents the total number of possible binary code combinations, i represents binary code combination. P_i indicates probability of particular binary code combinations and similarly P_i,t indicates the probability of particular binary code combinations at a specific time, t. (B) In the reconstruction method, average information rates are obtained from the signal to noise ratio (SNR). Signal and noise are calculated differently in each bound (see Passaglia and Troy, 2004 for how signal and noise are calculated). In here, S(f) means signals which are the Fourier transforms of the stimulus, R(f) means responses which are also the Fourier transforms of the response, respectively. Ŝ(f) means the best estimate of stimulus. In upper bound, Ŝ(f) is obtained by averaging R(f) [i.e,. R̄(f)]. In lower bound, Ŝ(f) is obtained by the linear decoder filter, H_s(f). N(f) represents noise, and noise is also different in each bound. In upper bound, noise is the difference between response and average response, while noise is the difference between signals and estimated stimulus in lower bound.