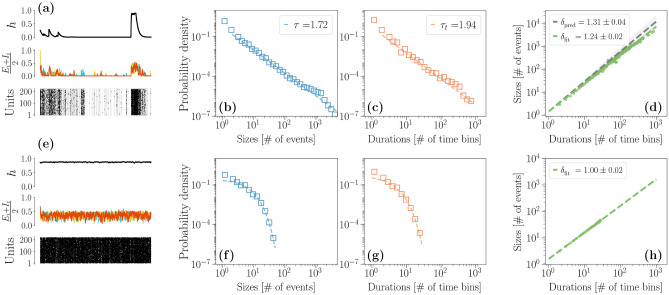
Figure 4.

Avalanche statistics generated by the Wilson Cowan units. The Wilson Cowan units are always in an inhibition dominated phase, i. e. ${\omega }_I=7$ and ${\omega }_E=6.8$, and $\alpha =1$. Their external input h is instead always in a balanced state, in particular ${\omega }_E^{(h)}=50.5$, ${\omega }_I^{(h)}=49.5$. Its other parameters are $h^{(h)}={10}^{-3}$ and ${\alpha }^{(h)}=0.1$. In Figures (a–d) however, ${\sigma }^{(h)}$, the amplitude of the noise, is increased to $2.5\times {10}^{-2}$ so that the up state can be destabilized by the noise. In Figures (e–h) instead the noise is reduced to $5\times {10}^{-3}$ so that the up state is stable. (a, e) Comparison between the trajectories of h, $\frac{E_i+I_i}{2}$ and the corresponding trains of events in the high (a) and low (e) ${\sigma }^{(h)}$ regime. (b–d) If ${\sigma }^{(h)}$ is high avalanches are power-law distributed and the crackling-noise relation is verified. (f–g) Same plots, now in the low ${\sigma }^{(h)}$ regime. Avalanches are now fitted with an exponential distribution. (h) The average avalanche size as a function of the duration scales with an exponent that, as ${\sigma }^{(h)}$ decreases, becomes closer to the trivial one ${\delta }_{\mathrm{fit}}\approx 1$.