Accounting for the Rarity of the Disease when Designing Clinical Trials with a Focus on Pediatric Cancers

Abstract

Background:

Clinical trials are challenging in rare diseases like pediatric cancers, where the accrual is limited. In these trials, inference assumptions are the same as in common diseases, that is the sample comes from a quasi-infinite population. This leads to overestimating the variance of the mean treatment effect. The finite-population correction factor correcting this bias is often used in surveys, but not in clinical trials. With few assumptions, the use of this correction factor can improve trials efficiency, showing that the power of those trials is sometimes higher than it appears.

Methods:

First, a simulation study assesses the standard error of the mean treatment effect and coverage of the 95% confidence interval with and without the correction. Second, the analytical power of a z-test with and without the correction is given. Finally, the impact on the sample size calculation is investigated. The impact of assuming a finite population is assessed for varying treatment effect, sample size and population size.

Results:

The simulation results confirm the overestimation of the standard error without the correction factor. When using the correction factor, the gain in power reaches up to 10.1%, 15.3% and 12.3% to detect a difference in treatment effect of 10%, 15% and 20%, respectively. The gain is negligible for n=30, in scenarios with high power (>95%), and for large populations. This gain in power translates into a decrease in sample size: if the conventional calculation leads to a sample size of 10% the population size, then the sample size can be divided by 1.1; if the conventional calculation leads to a sample size of 20% the population size, then the sample size can be divided by 1.2, in order to reach the planned type-I error and power.

Conclusion:

When dealing with rare diseases like pediatric cancers, the power of clinical trials might be higher than it appears if using conventional sample sizes. When correcting the variance of the mean using the population size, a gain in efficiency is observed with reasonable sample sizes and treatment differences for very small population sizes, showing that this approach can be useful for some pediatric cancer clinical trials.

Introduction

In conducting efficient clinical research in rare diseases, in pediatric cancer in particular, it is a challenge to recruit the number of patients needed to reach a satisfying conclusion in a timely manner. Therefore, efficient designs are key for testing new treatments for patients with rare diseases. In this work, it is suggested that the efficiency depends on the size of the population of interest, a parameter that is currently ignored in trial designs. If so, randomized trials for rare diseases might be more feasible than is typically thought.

Indeed, currently a trial assessing the efficacy of a new prostate cancer therapy that may affect a population of up to 190 000 newly diagnosed patients per year in the United States uses the same design as a trial planning to assess the efficacy of a therapy in desmoplastic small round cell tumor, a disease affecting a population of less than 100 patients per year. Both trials will require the same sample size if the anticipated efficacy of both treatments is similar. Surveys and epidemiology studies have accounted for the population size using a correction factor, the finite-population correction factor, which ensures a proper inference by correcting the variance of the mean parameter by adjusting for the fraction of the population included in the study.^1,2 However, this correction is mostly ignored in the clinical trial setting.

In this work, a simulation study assesses the impact of ignoring the population size on the precision of the estimation of the mean, through its standard error and confidence interval coverage. Secondly, analytical power and sample size calculations are derived and compared to the approach assuming a finite population. Finally, the feasibility and challenges of knowing the population size are considered in the discussion.

Methods

The use of asymptotic theory in finite populations requires some adjustments, mainly either using the finite-population correction factor (when sampling without replacement); or sampling with replacement,^1,3 an option which might not be straightforward in clinical trials.

The finite-population correction factor aims at correcting the inference of a parameter by accounting for the size of the population targeted by the inference. When making inference, the unobserved information is reflected by the variance of the mean. If an infinite population is always assumed, the inference is the same regardless of the size of the sampling population. The finite-population factor corrects this issue, by restricting the variance of the mean to the non-sampled subjects of the population.

Let’s consider a sample of n cases from a population of size N, and an outcome y_i measured for case i (i = 1, …, n in the sample and i = 1, …, N in the population). y_i are realizations of the random variable Y, with population mean μ and sample estimate $\overline{y}$. In addition, the variance of Y is noted by σ² and is estimated on the sampled data by s². When the population is assumed to be of finite size, the estimation of the variance of the mean accounts for both the sample size and the population size, as shown in Equation (1).

$$\widehat{var}(\overline{y})=\frac{N-n}{N-1}\frac{s^2}{n}$$ (1)

$c=\frac{N-n}{N-1}$ is the finite-population correction factor. c is approximately the proportion of the population that is not sampled. When n is fixed, N→∞ leads to c→1. This property explains why most often, when assuming the population is large enough, this correction factor c can be ignored, and the estimator of the variance of the mean is reduced to the commonly used $\frac{s^2}{n}$. While no strict rules exist to determine when a population is large enough to be considered infinite, it has been suggested that when the sample covers 5% or less of the sampling population, the impact of ignoring the correction factor c is minimal, and can c be ignored. Ignoring c allows inferences without knowing the population size. This correction factor can be applied in many inference contexts, including binomial and normal distributions, for confidence intervals and statistical testing, meaning it is applicable to most phase II and phase III clinical trials with binary or continuous endpoints.

Results

Estimation of the variance and coverage

A simulation study was conducted to assess the impact of not accounting for the population size on the standard-error of the mean and the coverage of the 95% confidence interval for the mean, ie the precision of the estimation of the parameter (see Supplemental Material). The standard error estimated without c on samples from the rare population always overestimates the empirical standard error, except in scenarios where the sample size is small. The standard error estimated with c is generally smaller and closer to the empirical estimate. The confidence interval coverage with c is either similar or closer to the targeted 95%. These results show that a more precise estimation is obtained using the correction, confirming its utility for small population inference, and confirming the existence of a bias in the standard error when it is ignored.

Power of the comparison between two treatment arms

The power of randomized trials, calculated analytically with and without using c, is presented in Table 1 for different response rates and sample sizes, but limited to a fixed, small population size (N = 500). The true response rate in arm A is 0.20, and the true response rate in arm B ranges from 0.30 to 0.60, showing a difference (or treatment effect) from 0.10 to 0.40. The total sample size ranges from 30 patients to 150. The type-I error is fixed at 0.025 one-sided. In these scenarios, assuming a very small population, the gain of using c is observed consistently, although it becomes negligible for small sample sizes or very large differences in response rate. It can be observed that in the case of a 15% difference, 176 patients would be enough to reach 80% power using c, while 271 patients would be necessary if ignoring c.

Table 1.

Power of comparison assuming an infinite population (without c) or assuming a population of finite size (with c).

pA	pB	Difference	Sample size	Power – infinite population	Power – finite population	Power Gain	Sample size needed for 80% power (infinite / finite)
0.2	0.30	0.10	30	0.093	0.096	0.003	581 / 269
0.2	0.30	0.10	50	0.128	0.137	0.009
0.2	0.30	0.10	75	0.170	0.192	0.022
0.2	0.30	0.10	100	0.213	0.254	0.041
0.2	0.30	0.10	125	0.255	0.323	0.068
0.2	0.30	0.10	150	0.296	0.397	0.101
0.2	0.35	0.15	30	0.152	0.159	0.007	271 / 176
0.2	0.35	0.15	50	0.225	0.245	0.020
0.2	0.35	0.15	75	0.314	0.359	0.045
0.2	0.35	0.15	100	0.399	0.477	0.078
0.2	0.35	0.15	125	0.478	0.594	0.116
0.2	0.35	0.15	150	0.550	0.703	0.153
0.2	0.40	0.20	30	0.231	0.243	0.012	157 / 120
0.2	0.40	0.20	50	0.352	0.384	0.032
0.2	0.40	0.20	75	0.491	0.555	0.064
0.2	0.40	0.20	100	0.609	0.705	0.096
0.2	0.40	0.20	125	0.705	0.822	0.117
0.2	0.40	0.20	150	0.782	0.905	0.123
0.2	0.50	0.30	30	0.442	0.464	0.022	72 / 63
0.2	0.50	0.30	50	0.649	0.694	0.045
0.2	0.50	0.30	75	0.818	0.875	0.057
0.2	0.50	0.30	100	0.912	0.959	0.047
0.2	0.50	0.30	125	0.959	0.990	0.031
0.2	0.50	0.30	150	0.982	0.998	0.016
0.2	0.60	0.40	30	0.688	0.714	0.026	40 / 37
0.2	0.60	0.40	50	0.885	0.915	0.030
0.2	0.60	0.40	75	0.972	0.987	0.015
0.2	0.60	0.40	100	0.994	0.999	0.005
0.2	0.60	0.40	125	0.999	1.000	0.001
0.2	0.60	0.40	150	1.000	1.000	0.000

Figure 1 further illustrates the impact of the population size on the power, when the difference to be detected is fixed at 0.20 or 0.10. As expected, the power assuming an infinite population (without c, dashed blue line) is stable over the population sizes, while the power assuming a finite population (with c, solid red line) decreases with population size for a fixed sample size. Overall, larger gains are observed for smaller population sizes, emphasizing the advantage of accounting for c when studying very rare diseases. In addition, for very small populations, the impact of a small difference in population size is smaller than the impact of ignoring the population size, arguing for an advantage even when the sample size is only known approximately.

Figure 1.

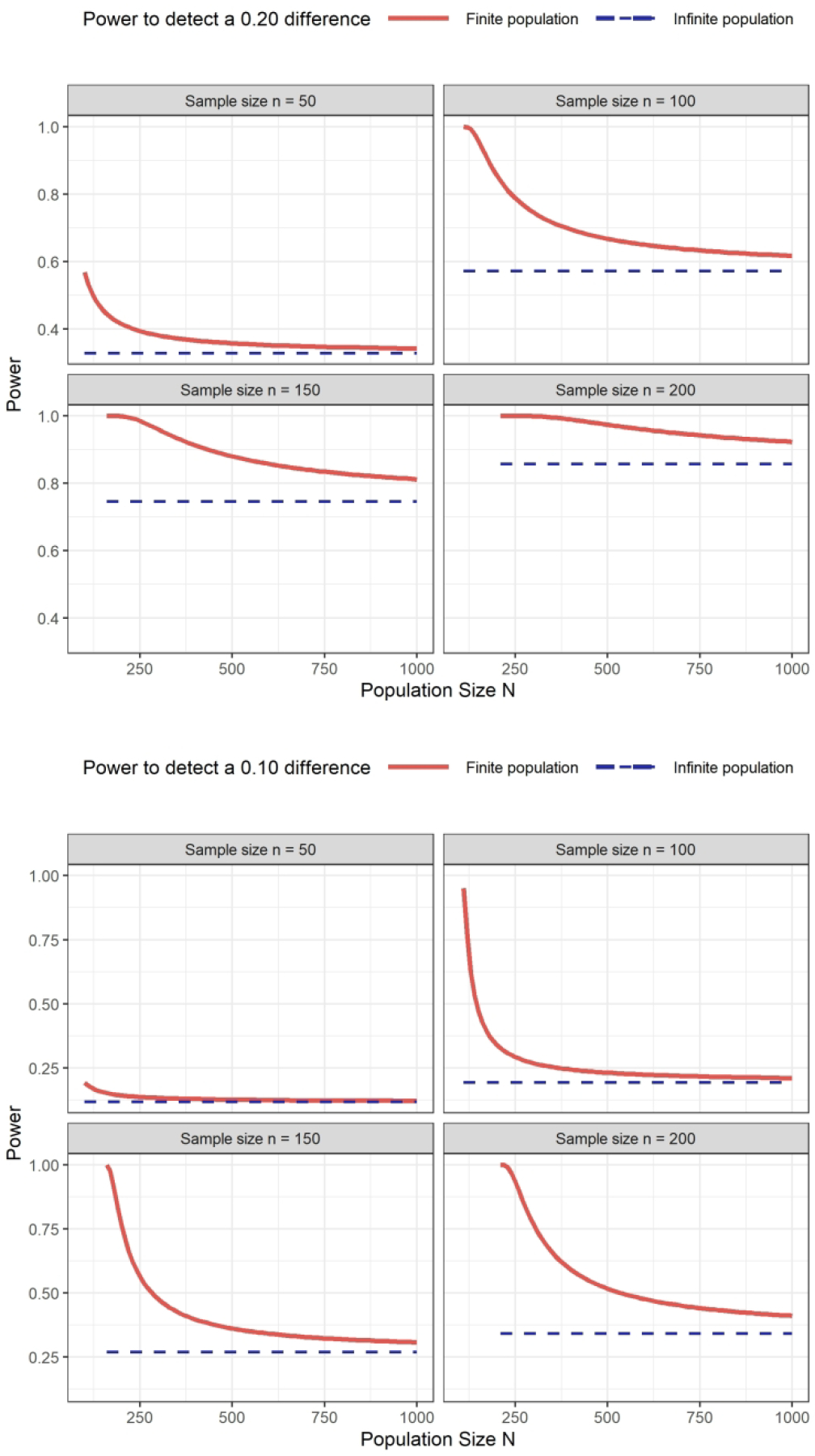
Power to compare two treatment arms for different population and sample sizes. Top panel: difference of 20%, from 25% to 45%; bottom panel: difference of 10%, from 25% to 35%.

Sample size consideration

Let n denote sample size for comparing a response rate between two arms using a z-test. Then, when replacing the variance of the mean by the variance using the finite-population correction, we obtained the following sample size:

$$n_c=\frac{n}{1+\frac{n-1}{N}}$$ (2)

The decrease in the sample size resulting from using the correction is directly proportional to the initial proportion of the population that the required conventional sample size represents. For example, if the conventional sample size n is such that $\frac{n-1}{N}=0.1$, i.e. approximately 10% of the sampling population, then only 91% of this sample size is needed (n/1.1 = 0.91n). If the conventional sample size is 20% of the population, then the corresponding required sample size is 0.83n. The relation between the sample size n without c and the sample size n_c with c is shown in Figure 2. It is also maintained in the context of comparing one estimate to a control value in a one-arm trial.

Figure 2.

Needed sample size n_c according to the sample size n − 1 calculated without c, both expressed as a proportion of the population size (the gray line represents a sample size n_c equal to the sample size without c).

Discussion

This study confirms that, when the population from which a trial is accruing is small, failing to account for the population size leads to a biased variance of the mean and a higher required sample size. Advantages of using a population size correction are mainly observed for very small populations, arguing in favor of using the finite-population correction factor for very rare diseases. However, barriers exist to its use, mainly the necessity to know the sampling population size. In addition, since patients are accrued over time the definition of the population itself is a challenge.

The sampling population is the set of individuals for which the inference is made. Statistical inference in clinical trials assumes that individuals in the sampling population have an equal chance to be part of the sample/trial. Although the population is rarely explicitly defined in trial protocols, it is implicitly assumed. In that regard, the proposed approach is not different to other trial designs, except that the population definition must be explicit. To limit the challenges due to long accrual duration and shift in the population, the proposed approach might be better suited for short-term outcomes such as response rate or change in biomarkers, and for early phase trials.

The use of the finite-population correction factor is most advantageous for very rare diseases. In these settings it is especially important to make the available participants’ contribution as efficient as possible. Examples of cancers with very low incidence are provided by the European Cooperative Study Group for Pediatric Rare Tumors (EXPeRT), which consider very rare pediatric cancers as having an annual incidence of less than 2 in a million up to the age of 18.⁴ According to this consensus, these cancers represent 11% of all cancers in patients 0–19 years in Europe. Examples include cancers typical in children (eg, hepatoblastoma, 0.9 case per million), and tumors that are more common in adults such as neuroendocrine tumors (2.0 per million), while osteosarcoma, for example, had an incidence of 4 per million. Desmoplastic small round cell tumors (0.3 cases per million in the United States⁵) is another example of a very rare tumor. Trial investigators can assess whether their trial population is sufficiently well defined to apply the proposed approach, as this is not a solution that can be universally applied. An extension of the proposed approach would be to incorporate the uncertainty in the population size into the finite-population correction.

In conclusion, the proposed approach of using a population size correction can help improve the feasibility and success of challenging trials in very rare diseases. While it can seem rational to take the conservative approach of assuming an infinite population in order not to underestimate the standard-error of the mean and the level of evidence, this is not always the most efficient option. When patient resources are limited, the reduction in target sample size can contribute to study feasibility.