Limits of Decoding Mental States with fMRI

Abstract

A growing number of studies claim to decode mental states using multi-voxel decoders of brain activity. It has been proposed that the fixed, fine-grained, multi-voxel patterns in these decoders are necessary for discriminating between and identifying mental states. Here, we present evidence that the efficacy of these decoders might be overstated. Across various tasks, decoder patterns were spatially imprecise, as decoder performance was unaffected by spatial smoothing; 90% redundant, as selecting a random 10% of a decoder’s constituent voxels recovered full decoder performance; and performed similarly to brain activity maps used as decoders. We distinguish decoder performance in discriminating between mental states from performance in identifying a given mental state, and show that even when discrimination performance is adequate, identification can be poor. Finally, we demonstrate that simple and intuitive similarity metrics explain 91% and 62% of discrimination performance within- and across-subjects, respectively. These findings indicate that currently used across-subject decoders of mental states are superfluous and inappropriate for decision-making.

1. Introduction

Recent neuroimaging studies either explicitly claim or strongly imply that mental states can be decoded from patterns of brain activity. By fitting complex statistical models to functional magnetic resonance imaging (fMRI) brain scan results, these studies attempt to decode feelings, thoughts, decisions, intentions, and behaviors (Gabrieli, Ghosh, & Whitfield-Gabrieli, 2015; Gianaros et al., 2020; Haynes et al., 2007; Kragel, Koban, Barrett, & Wager, 2018). If truly successful, such approaches would break the code of mental states and suggest the ability to “read the brain” of every human being, at least for the mental states for which such models have been constructed. Here, we systematically examine the validity of such claims.

Decoding predicts unknown experimental variables from brain responses. In contrast, encoding models the statistical dependence of brain responses on experimental variables. In either case, decoders and encoders are typically created from task fMRI studies, in which investigators deliver a stimulus (independent variable) and observe brain activity (dependent variable) (Hu & Iannetti, 2016; Naselaris, Kay, Nishimoto, & Gallant, 2011). Encoding models are consistent with this data-generating process while decoding flips the independent and dependent variables. This switching of variables is also referred to as reverse inference. Conceptually, decoding and reverse inference are one and the same: The use of brain activity—a response to a stimulus—to predict the applied stimulus. However, it has been argued that decoding is “principled” because the encoding map is not used as the model; instead, a decoding model is created (Poldrack, 2011; Varoquaux & Thirion, 2014). Yet, decoding itself is still incompatible with the data-generating process and introduces difficult statistical and epistemological problems. Statistically, can we build a model that is both sensitive and specific? Epistemologically, what can we learn about the brain from decoding? This paper will unpack the former question, providing an in-depth analysis of decoders, their properties, and different decoding tasks. From our analyses, we draw broader conclusions and provide general recommendations for decoding studies.

Statistically, encoding models brain activation patterns caused by external stimuli or internal cognitive processes. This is accomplished through mass-univariate general linear models of brain responses. Since a voxel’s activation time series is analyzed as a function of one or more explanatory variables, the problem is well-posed—encoding models have unique solutions that continuously map the stimulus to the response (if maximum number of explanatory variables is less than or equal to the number time points). On the other hand, when predicting a stimulus (or mental process) from voxel responses, the number of voxels—in this case the explanatory variables—is usually much larger than the number of observations, which leads to an ill-posed problem with infinite solutions. Thus, for most decoding problems, there are an infinite number of possible decoders, yielding the superiority of any decoder or set of decoders, along with the properties that make a decoder unique, uncertain.

Decodability—how discernable a mental state is, given a brain activity pattern—is predicated both on the brain activity properties of the task being discerned as well as the goal of the decoding. Intuitively, decodability is analogous to discerning a breed of dog; breeds that look more similar will be harder to distinguish. The literature claims decoders can (1) discriminate between mental states, (2) identify mental states, and (3) capture additional state-related measures (stimulus or perception intensities). A dog breed metaphor can more tangibly elucidate these goals: Consider a pug (a decodee) and a French Bulldog (a comparator)—two breeds that may look alike. If one is familiar with a pug’s unique physical features—small stature, short snout, wrinkled face, folded ears, curled tail, etc.—then such features can serve as the decoder for a pug. This decoder can then be used to perform the three decoding tasks. Specifically, discrimination (goal 1) is akin to deciding which dog is a pug when the pug and French Bulldog are next to one another. Identification (goal 2), instead, is akin to saying whether a single dog is a pug when there are no other dogs around, and it is intuitive that one must be more confident of the properties of pugs not to mistakenly label a French Bulldog as a pug. Finally, capturing a continuous measure (goal 3), such as perceived intensity of a state, is much like trying to judge a dog’s age. Although discrimination and capturing continuous measures have been discussed and illustrated for various mental states, less attention has been given to identifying a certain mental state from a given pattern of brain activity.

The pattern of mental state decoders arises from weights assigned to its constituent voxels. In this paper, we deal with a specific class of decoders that we call fixed-weight decoders—each voxel is assigned its own weight. Voxel weights are derived in three stages. First, general linear models (GLM) generate a brain activity map (correlation between the activity in each voxel and the task). This is a basic encoding model since the task is the independent variable and voxels are dependent variables. Second, GLM is used to contrast the activity maps from a task or state of interest (a decodee; e.g., pain) to one of no interest (a comparator; e.g., touch), and its results are thresholded (a contrast map). The thresholded contrast map is used to constrain the spatial extent of the decoder. Finally, “machine learning” models are used to tune the weights in the thresholded contrast map to optimize its predictive performance (Liang, Su, Mouraux, & Iannetti, 2019; Wager et al., 2013); the result is a relatively sparse, fixed-weight decoder with a fine-grained pattern (a decoder). These models are a conceptual demarcation from the activity map since they are a form of decoding (reverse inference) rather than encoding. It is tacitly assumed that each stage improves performance of the decoder by uncovering better distributed patterns of neural ensembles related to the mental state of interest, and as a result, detailed spatial patterns confer predictive value, as explicitly posited to be one possible explanation for decoding performance, “the pattern of activation, rather than the overall level of activation of a region, is the critical agent of discrimination.” (Wager et al., 2013, p. p. 1395) This concept is now expounded for diverse topics across many labs (Eisenbarth, Chang, & Wager, 2016; Gianaros et al., 2020; Kragel et al., 2018; Lindquist et al., 2017; Marquand et al., 2010; Poldrack, Halchenko, & Hanson, 2009; Wager et al., 2013; Wager et al., 2015; Woo, Roy, Buhle, & Wager, 2015).

The notion that across-subject decoders can capture mental states across different individuals violates basic neuroscientific principles, since it is premised on the immutability and uniformity of human brains. Within-subject decoding requires a one-to-one mapping between brain activity patterns and brain states that needs to be preserved across time. Preservation of mapping across time is vulnerable to time effects such as learning, repetition suppression, etc. For across-subject decoding, this mapping additionally needs to be conserved across individuals. This ignores inter-subject variability in structural and functional anatomy due to differences in genetics, lifestyles, experiences, and associated memory traces (Gazzaniga, 2000; Kandel, 2013), each of which would carve the individualized brain activity of subjective brain states (for a discussion on the topic from the viewpoint of fMRI analysis, see (Feilong, Nastase, Guntupalli, & Haxby, 2018)). If a trivial, fixed relationship exists between subjective brain states and brain activity, such decoders also raise strong ethical and legal concerns regarding their ability to invade mental privacy (Mecacci & Haselager, 2019) and would be incongruent with commonly accepted philosophical constructs of subjective brain states (Chalmers, 1997).

Our principal aim was to evaluate the performance and necessity of fixed-weight decoders relative to more parsimonious approaches (e.g., using encoders or brain activity maps as decoders). After rigorously evaluating the performance of decoders, we sought to understand fixed-weight decoders from a more general perspective: What determines and constrains decodability?

2. Materials and methods

2.1. Datasets

6 datasets were used in this paper; all are part of published studies and were either provided by their authors (Datasets 1, 2, 3, 4, and 5) or downloaded from public repositories (Dataset 6). Datasets 1, 2, 3, 4, and 5 consist of voxel-wise, whole brain, task dependent GLM analysis activation maps (beta maps). Dataset 6 consists of BOLD timeseries which were processed using standard fMRI pre- and post-processing methods described below.

2.1.1. Dataset 1

15, right-handed, adult subjects (mean age: 35.21 ± 11.48 years, 7 females). Subjects had no history of pain, psychiatric, or neurological disorders. FMRI data were collected while subjects received thermal stimuli across 3 temperatures: 47, 49, and 51 degrees Celsius. Subjects continuously rated, using a finger span device (Apkarian, Krauss, Fredrickson, & Szeverenyi, 2001; Baliki et al., 2006), their pain from 0, not painful, up to 100, worst imaginable pain (“pain rating” task.) A control scan was performed while subjects used the finger span device to track a moving bar projected on the screen (“visual rating” task; moving bar replicated for each subject the specific pain rating task temporal pattern). The dataset includes one GLM beta map per subject per stimulus type. The dataset was previously described in (Baliki, Geha, & Apkarian, 2009).

2.1.2. Dataset 2

51 healthy, right-handed, adult subjects (mean age: 24 ± 2.29 years, 34 females). Subjects had no history of brain injuries, pain disorders, or psychiatric or neurological diseases. FMRI data was collected while subjects received painful heat stimuli on the right foot dorsum using a CO2 laser, as well as tactile stimuli to the same area using electrical stimulation. Stimuli were not delivered at the same time. Perceived intensities were recorded for every stimulus and only the stimuli with matched perceived intensity for painful heat and touch were selected for GLM analysis. The dataset includes one activation map per subject per stimulus modality – painful heat and touch. The dataset was previously described in (Liang et al., 2019; Su et al., 2019).

2.1.3. Dataset 3

14 healthy, right-handed, adult subjects (age: 20 – 36 years old, 6 females). FMRI data were collected while subjects received painful heat stimuli on the right foot dorsum using a CO2 laser, tactile stimuli to the same area using electrical stimulation, visual stimuli using a white disk presented above the right foot, and auditory stimuli delivered via pneumatic earphones. Stimuli were not delivered at the same time. Perceived intensities were recorded for every stimulus and only the stimuli with matched perceived intensity across the four modalities were selected for GLM analysis. The dataset includes one activation map per subject per stimulus modality – painful heat, tactile, auditory, and visual. The dataset was previously described and published in (Liang et al., 2019).

2.1.4. Dataset 4

33 healthy, right-handed, adult subjects (mean age: 27.9 ± 9.0 years, 22 females). Subjects had no history of pain, psychiatric, or neurological disorders. FMRI data was collected while subjects received thermal stimuli that varied in one-degree Celsius increments across six temperatures from 44.3 degrees Celsius up to 49.3. Subjects then evaluated each stimulus as warm, and scored it from 0, not perceived up to 99, about to become painful, or as painfully hot, and scored it from 100, no pain, up to 200, worst imaginable pain. The dataset includes an average GLM activation map per subject per stimulus temperature, as well as the corresponding average stimulus ratings. When this dataset was applied dichotomously (pain vs. no pain), we averaged the brain activity maps from the painful and nonpainful conditions; we omitted subjects who had fewer than two brain activity maps for each condition, resulting in 29 subjects for dichotomous ratings. The dataset was previously described in (Wager et al., 2013; Woo et al., 2015).

2.1.5. Dataset 5

14 healthy, right-handed, adult subjects (mean age 22.4 years, range 19–35, 10 females). Subjects had no history of neuropsychiatric disorders, and were not on psychoactive medications. FMRI data was collected while at each trial subjects were presented with a word and had to decide if it refers to a living or nonliving entity. Each word was presented either mirrored or plain. The direction of presented words were interspersed such that we end up with four trial scenarios: Plain-Repeat (PL-RP) where during the trial and the one immediately preceding it, the words were plain; Mirror-Repeat (MR-RP) where during the trial and the one immediately preceding it, the words were mirrored; Plain-Switch (PL-SW) where during the trial the word is plain, and the trial immediately preceding it, the word is mirrored; Plain-Switch (MR-SW) where during the trial the word is mirrored, and the trial immediately preceding it, the word is plain. Data was collected across twelve runs, two training weeks separated two sets of six runs. Dataset includes, up to 12 GLM activation maps (minimum 10) per subject per scenario. The dataset was previously described in (Jimura, Cazalis, Stover, & Poldrack, 2014a). This dataset was provided in subject space. We performed a nonlinear registration of the brains into standard MNI space, 2×2×2 mm³, using FSL FNIRT (Andersson, Jenkinson, & Smith, 2007).

2.1.6. Dataset 6

213 healthy, adult subjects (mean age 24.1 year (SD = 7.4 year), 101 females). Subjects had no history of physical or mental health condition. fMRI data was collected while subjects performed a voice localizer task. Forty blocks of vocal sounds (20) and non-vocal sounds (20) interspersed with periods of silence were presented while the subjects laid silent and passively listening with their eyes closed in the scanner. This dataset was previously described in (C. R. Pernet et al., 2015). Raw fMRI data was downloaded from openneuro.org (https://openneuro.org/datasets/ds000158/versions/1.0.0). We used minimal pre-processing for this study which was performed using the FMRIB 5.0.8 software library (FSL) (Jenkinson, Beckmann, Behrens, Woolrich, & Smith, 2012), MATLAB2018a and in-house scripts. The following steps were performed: motion correction, intensity normalization, nuisance regression of 6 motion vectors, signal-averaged overall voxels of the eroded white matter and ventricle region, and global signal of the whole brain, and band-pass filtering (0.008–0.1 Hz) by applying a 4^th-order Butterworth filter. All pre-processed rs-fMRI data were registered to the MNI152 2mm template using a two-step procedure, in which the mean of preprocessed fMRI data was registered with a 7-degrees-of-freedom affine transformation to its corresponding T1 brain (FLIRT); transformation parameters were computed by nonlinearly registering individual T1 brains to the MNI152 template (FNIRT). Combining the two transformations by multiplying the matrices yielded transformation parameters normalizing the pre-processed fMRI data to the standard space. Task related activation maps (vocal vs silence, and non-vocal vs silence) were derived from a whole brain GLM regression analysis using the FMRIB Software Library (FSL) (Jenkinson et al., 2012; Smith et al., 2004; Woolrich et al., 2009).

2.2. Decoders

2.2.1. Neurologic Pain Signature (NPS)

Neurologic Pain Signature, NPS, was shared with us by Tor Wager, whose team developed this across-subject fwMVP (Wager et al., 2013), and has studied its decoding abilities in multiple publications.

2.2.2. Pain-preferring voxels (pPV)

Pain-preferring voxels, pPV, is an as-fwMVP decoder developed by Iannetti and colleagues (Liang et al., 2019).

2.2.3. “Pain” Neurosynth map (pNsy)

We used the term-based meta-analysis platform Neurosynth (Yarkoni, Poldrack, Nichols, Van Essen, & Wager, 2011) to identify a reverse inference brain activity pattern for the term “pain”, using association test. We term the obtained pattern as pain-Neurosynth, or pNsy, decoder. Neurosynth uses a probabilistic framework based on Generalized Correspondence Latent Dirichlet Allocation and extracts latent topics from a database of 14,371 published fMRI studies (neurosynth.org, (Yarkoni et al., 2011)). The term “pain” identified 516 studies based on which a brain pattern was generated. The reverse inference association map (FDR corrected <0.01) was used as pNsy, which identifies voxels and their probabilities for being included in the 516 “pain” term associated studies but not in the rest of the >11,000 studies.

2.2.4. Gaussian process decoder

We used a probabilistic Gaussian Process-based (GP) modeling algorithm (Rasmussen, 2003; Jessica Schrouff et al., 2013) to derive an across-subject fwMVP decoder from the contrast between thermal pain ratings and ratings of visual bars in Dataset 1. We used the publicly available Matlab toolbox PRoNTo (ver2.1.1) (Jessica Schrouff et al., 2013; J. Schrouff et al., 2013). We label derived fwMVP decoder pain-GP, or pGP.

2.3. Use of decoders

2.3.1. Normalized dot product

Throughout this study, we use the normalized dot product (NDP) (eq. 1) as a measure of similarity between templates and brain activation patterns. The NDP is calculated between the vectorized forms of a given decoder template and a stimulus specific brain activation map. The NDP is a scalar between −1 for colinear vectors of opposite direction, and 1 for colinear vectors of same direction. An NDP value of zero means the 2 vectors are orthogonal to each other – no similarity.

$$NDP=T\cdot \beta =\frac{{\sum }_{i=1}^n{T}_i\cdot {\beta }_i}{\sqrt{{\sum }_{i=1}^n{T}_i^2\cdot {\sum }_{i=1}^n{\beta }_i^2}}$$ eq. 1

Where T and β are the vectorized forms of the decoding template and a stimulus specific activation map, T_i and β_i are the components of T and β, and n is the number of voxels comprising the brain.

2.3.2. Binary classification

Two types of binary classifications were performed. The first is a between groups binary classification of brains in painful vs non-painful conditions (or some other decode-comparator pair). We start by calculating the NDP for each brain under each condition; We then use the NDPs as scores to build the Receiver Operator Curve and calculate the area under the curve (AUC). The second classification is a Forced Choice classification, this is a threshold free classification, where the NDP of two brains are compared to each other, and the one with the highest value is classified as “in pain”, or as experiencing a higher level of pain than the second brain.

2.3.3. Meta-analysis

Meta-analysis was performed to obtain average performance estimates for each of the three primary decoders. We modeled each decoder separately since they are ‘competing’; as such, the effect of covariance on model parameter estimates is undesirable. Because Dataset 3 contained three comparator tasks, we averaged their performance and estimated the variance of this estimate using the bootstrap technique (1000 replicates); thus, the variance estimate of the average accounts for covariance between the three comparator conditions. No variance stabilizing transformation was performed since the bootstrap distribution of each AUC was approximately normal and transformations provided little gain on average. Both NPS and pNsy were modeled using Datasets 1–4, and pPV was modeled using Datasets 1, 2, and 4, as pPV was derived from Dataset 3. In other words, to use Dataset 3 in the pPV meta-analysis would bias the results in favor of pPV, and we wanted each estimate to be unbiased. We performed a random-effects meta-analysis, fit using restricted maximum likelihood in the metafor package using the raw AUCs (Viechtbauer, 2010).

2.3.4. Bayesian classification for identification

We created a nonparametric Bayesian classification model to probabilistically classify subjects as being in a certain state given their brain activity map. This model was trained and run on all subjects across all pain Datasets (Fix & Hodges, 1951; Silverman, 1986), in addition to the voice dataset (Cyril R Pernet et al., 2015).

Starting with the pain datasets, we started with a matrix containing all subjects, tasks, and their respective normalized dot products (NDP). Each subject was sampled one at a time. Using the remaining subjects, a probability density functions (pdf) of normalized dot products was created for each task. To create these pdfs, we used kernel density estimation with a Gaussian kernel and a bandwidth chosen using the Sheather-Jones method (Sheather & Jones, 1991). Specifically, a pdf was created for each of the comparator conditions (visuomotor, touch, audition, vision, and nonpainful heat) and pain. All of the pain conditions were modeled as one distribution, as a tacit assumption of these decoders is that “physical pain” is a single construct. From these distributions, we could calculate a posterior probability, P(pain | NDP), for each individual i: (eq 2)

$$P\left(\mathit{\text{pain}}\mid ND{P}_i\right)=\frac{{\widehat{f}}_{\mathit{\text{pain}}}\left(ND{P}_i\mid \mathit{\text{pain}}\right)P(\mathit{\text{pain}})}{{\sum }_{j=1}^k{\widehat{f}}_j\left(ND{P}_i\mid {\mathit{\text{task}}}_j\right)P\left({\mathit{\text{task}}}_j\right)}$$ eq. 2

where ${\widehat{f}}_{\mathit{\text{pain}}}\left(ND{P}_i\right)$ and ${\widehat{f}}_j\left(ND{P}_i\right)$ are the kernel density estimates used for NDP_i (i.e., derived from all other brains) in pain or task j (where tasks j = 1, …, k include all comparator tasks and pain). Priors, P(·), were derived from the number of studies in Neurosynth that contains:

• “pain” = 516

• “tactile” OR “touch” = 110 + 225

• “visually” OR “vision” = 333 + 137

• “auditory” = 1253

• “visuomotor” = 153

• “heat” (from old Neurosynth) = 61

All study counts were obtained on December 10, 2019. Because they were obtained from Neurosynth and each study is given equal weight, the priors assume an equal number of subjects across studies, and thus estimates the probability of a brain undergoing each of these tasks in the “neuroimaging world,” if we consider these tasks to be the neuroimaging world. Of note, these priors provided more optimistic estimates as compared to uniform priors.

For both NPS and pNsy, all subjects were used to obtain the posterior distribution. However, to obtain an unbiased posterior distribution for pPV, we did not include subjects from Dataset 3 (i.e., from which pPV was derived).

This process was repeated for the voice test dataset (106 subjects). However, because the tasks in the voice dataset were unique, we used a flat prior (i.e., prior probability = ½ for each of the two tasks).

2.3.5. Calculation of distributional overlap for identification

We calculated the overlap between the distributions of decodee and comparator NDPs as a marker of identifiability. The overlapping region of probability density functions contains information that cannot be used to identify; thus, lower overlap corresponds to higher identifiability. To calculate overlap, we first fit each NDP distribution (e.g., NPS pain and NPS nonpain, separately) using kernel density estimation with an Gaussian kernel and a bandwidth chosen using the Sheather-Jones method (Sheather & Jones, 1991). We then had ${\widehat{f}}_{\mathit{\text{decodee}}}(\cdot )$ and ${\widehat{f}}_{\mathit{\text{comparator}}}(\cdot )$, kernel density estimates for the decodee and comparator, respectively. We integrated over their minimum to calculate their overlap:

$$\underset{-1}{\overset{1}{\int }}\text{min}\left({\widehat{f}}_{\text{decodee }}(x),{\widehat{f}}_{\text{comparator }}(x)\right)dx$$ eq.3

2.3.6. Normalized dot product – stimulus relationship

In this analysis we wanted to investigate the relationship between the NDP and stimulus rating as well as stimulus intensity. Dataset 4 includes information about stimulus intensity and stimulus rating. We fit the data using locally estimated scatterplot smoothing (LOESS) (Cleveland & Devlin, 1988).

2.3.7. Within study vs. across study decoders

Given that pNsy is based on a meta-analysis of study-level GLM brain activity maps, we created decoders from four datasets by averaging subject-level GLM brain activity maps obtained from a pain task. These study-level decoders were then used to classify brains as pain vs. no pain, in accordance with the task.

for each study i
        average beta maps for the pain task in study i
end
for each study i
        for each study j
                for each subject k in study j
                        for each task l in subject k
                                calculate cosine similarity of between TASK_lk and DECODER_i
                        end
                end
                calculate AUC for DECODER_i applied to STUDY_j
        end
end

2.3.8. Within subject vs across subject decoders

Given the variability of fMRI data, both within-subject and across-subject, we wanted to answer the following question: will decoding mental states of a particular subject using a template derived from data of the same subject be more accurate than decoding of mental states of a group of subjects using a template derived from the group’s data? Are within-subject decoders superior to between-subject decoders? The following analysis addresses this question using Dataset 6.

2.3.9. Within subject decoding

Below is a pseudo-code for the within subject analysis.

for each subject i
        for each task j
                randomly select half the task j beta maps replicates,
                average voxel-wise to get inter subject i, task j specific decoding template Tj,
                label the remaining task j replicates as TASK_j,
                calculate Signature Responses (SR) of each beta map in TASK_j using Tj,
                for each task k ≠ j
                        randomly select half the task k beta maps replicates and label as TASK_k,
                        calculate SRs of each beta map in TASK_k using Tj,
                        calculate AUC for correctly classifying TASK_j and TASK_k beta maps,
                end
        end
end
Average the AUCs along all subjects,
repeat from the start 1,000 times.

This will result in average AUC estimates for the classification of each possible task pairs (i,j) using both T_i and T_j. All performed within-subject.

2.3.10. Between subject decoding

Below is a pseudo-code for the between subject analysis.

for each subject i
        for each task j
                average beta map replicates to get one beta map per subject per task to form the between-subjects dataset,
        end
end
for each task j
        randomly select half the task j beta maps (from the between-subjects dataset),
        average voxel-wise to get between-subjects task j specific decoding template Tj,
        label the remaining task j replicates as TASK_j,
        calculate SRs of each beta map in TASK_j using Tj,
        for each task k ≠ j
                randomly select half the task k beta maps replicates and label as TASK_k,
                calculate SRs of each beta map in TASK_k using Tj,
                calculate AUC for correctly classifying TASK_j and TASK_k beta maps,
        end
end
repeat from the start 1,000 times.

This will result in AUC estimates for the classification of each possible task pairs (i,j) using both T_i and T_j. All performed between-subject.

2.4. Decoder perturbations

2.4.1. Pattern smoothing

To evaluate the importance of the spatial pattern of fwMVPs on the performance of task classification, NDPs were calculated using spatially smoothed versions of a given decoder. Our hypothesis is that, if a pattern holds task specific information, then spatial smoothing will diminish the performance of the classifier. Smoothing was done using a 3D isotropic Gaussian kernel filter applied to each template in standard space (eq. 4).

$$T_f(x,y,z\mid \sigma )=\frac{(T*G(\sigma ))(x,y,z)}{(M*G(\sigma ))(x,y,z)}\cdot M(x,y,z)$$ eq. 4

Where T and T_f are the original and filtered decoder respectively, G is the Gaussian kernel, M is a binary mask that is True where the decoder is non-zero and False everywhere else, x, y, z are voxel coordinates, and σ is the kernel standard deviation. The additional M in the numerator resets all non-decoder voxels to zero after filtering – preventing the decoder from bleeding out of its boundary. The convolution in the denominator is the sum of the kernel coefficients where it overlaps with the decoder; this normalization leads to a weighted average using only voxels within the decoder. Together, the additional M in the numerator and the convolution in the denominator correct for boundary effects during filtering. In addition to the original decoder, patterns were progressively smoothed by varying the kernel standard deviation from 1 mm up to 20 mm. Gaussian smoothing is in effect a spatial low pass filter with a spatial frequency cutoff at −3dB given by:

$$f_c(\sigma )=\frac{\sqrt{2\mathit{\text{ln}}(2)}}{2\pi \sigma }$$ eq. 5

Increasing the Gaussian kernel standard deviation will lead to a lower cutoff frequency, effectively reducing the spatial resolution of the data.

A binarized version of each decoder was also used to simulate a filter with infinite standard deviation, as well as the sign of each filtered decoder at each filter level (sgn(T_f)), where voxels that are positive become 1, and voxels that are negative become −1, and zero everywhere else. The signed version of the templates was motivated by the fact that in contrast with pPV and pNsy, almost half of the NPS voxels are negative (22,725/47,490), and we needed to investigate the role of sign of the coefficients excluding the effect of the absolute value on decoding. The NDPs generated from these spatial filters were used to calculate the AUC at each smoothing level.

2.4.2. Information redundancy

We investigated the extent of information redundancy for the three pain the decoders. We wanted to examine whether the spatial extent of a given decoder was needed, and what percent, on average, of the total number of voxels in each decoder was necessary before the classifier performance becomes comparable to the full decoder. Our hypothesis is that if there is no information redundancy, the performance will reach its maximum only when we include the entire decoder; and with increasing redundancy this maximum will be reached with a lower percentage of voxels on average.

Based on the raw, the unfiltered sign, and the infinitely filtered version of each as-fwMVP, we constructed a series of new decoders that included an increasing number of voxels randomly selected from the parent fwMVP without replacement, all remaining voxels were set to zero. We started with ten voxels and increased to the maximum number of voxels in a template. This random sampling was repeated 1,000 time, which produces as many NDPs for each density level. The NDPs were then used to calculate the ROC and its area, which were then averaged to give the average AUC at each percentage level and also calculate associated uncertainty.

2.4.3. Voxel weights

We investigated whether or not voxels with higher coefficients (in absolute value) encode more state specific information compared to voxels with lower coefficients. To address this question, we binned each fwMVP voxels by their absolute weights, such that the top 10% of absolute voxel weights were in the first bin, the second 10% were in the second bin, etc., and built a decoder from each tier. We then used those templates to calculate the NDPs and the AUCs as a function of voxel coefficient tier. In addition to the 10% bin width and unfiltered decoders, we also generated decoders using bin widths of 1%, 5%, and 20%, as well as decoders from the sign of the unfiltered, and infinitely filtered versions.

2.4.4. Role of brain areas

We investigated whether decoder voxels from certain brain regions perform better than others. We selected pNsy as the decoder for this analysis given the probabilistic meaning of its voxel weights. We thresholded the decoder (voxel weights z > 6) and generated a new decoder from each distinct cluster; we ended up with seven new decoders. We then evaluated the pain decoding performance of each new decoder on datasets 1 to 4. We applied a Gaussian spatial filter (sd = 10 mm) before thresholding, otherwise we end up with too many fragmented clusters. We also built 7 decoders from NPS and pPV using the overlap between each of them and each of the 7 cluster from pNsy. We used pNsy clusters because it is the decoder with the most voxels in common with NPS and pPV.

2.5. Decoders derived from Dataset 5 and Dataset 6

We created fwMVP decoders from Dataset 5 (Jimura et al., 2014a) and Dataset 6 (C. R. Pernet et al., 2015) to assess the generalizability of our results to other cognitive domains. In Dataset 5 we are interested in decoding “reading a mirrored text (mr) after reading a mirrored text (mr-mr)” vs “reading a mirrored text after reading a plain text (mr-pl)” or pl-mr or pl-pl. In Dataset 6, we are interested in decoding “hearing vocal sounds” vs “hearing non-vocal sounds”. Four approaches were used to create these decoders: Support Vector Machine, LASSO-PCR, Gaussian Process Classification, as well a GLM contrast of activation maps. Training and testing of the decoders were similar across all four approaches, with some minor differences in the treatment of each dataset in how we select the training and testing groups. Assuming we have our training and testing groups, the procedure is as follows:

1. Perform a second-level group analysis with cluster-based thresholding corrected for multiple comparisons by using the null distribution of the maximum cluster mass (FSL randomize (Woolrich, Behrens, Beckmann, Jenkinson, & Smith, 2004), option -C) on the training group for the contrast GLM activation maps mr_rpt > (mr_sw, pl_rp, pl_sw) for Dataset 6, and vocal_sound > non-vocal for Dataset 7.

2. Binarize the group contrast map; this will be the mask of voxels of interest for building our decoders.

3. Use SVM, LASSO-PCR, Gaussian Process to generate the decoder with the activation maps (GLM) of the training group. For GLM decoders, the mean difference in activation maps within this same masked region was used.

4. Perform the normalized dot product of the decoder with the activation maps in the testing group to calculate the signature response and calculate the AUC of the classification exercise.

Dataset 5 include several replicate activation maps per task for each of the 14 subjects, we preprocessed the data as follows:

1. Average all task replicates for each subject.

2. Randomly split the subjects into two seven subject groups: training and testing.

3. Create a template and test it as described above.

4. Repeat 100 times from step 2 and build the AUC distribution.

After preprocessing, Dataset 6 included 213 subjects and had one activation map per stimulus per subject. The large number of subjects allows us to split it into a training group (107 Subjects), and a validation group (106 Subjects) without the need for permutation. Because the sample was large, we calculated the AUC confidence interval using its relationship with the Wilcoxon statistic and normal assumptions (eq. 6)

$$95\%CI=AUC\pm 1.96\sqrt{\frac{AUC}{n^2}\left((1-AUC)+(n-1)\left(\frac{1}{2-AUC}+\frac{2AUC}{1+AUC}-2\right)\right)}$$ eq. 6

where n is the number of individuals in the validation sample, each of whom have one activation map for each state.

2.5.1. SVM and Gaussian process

We used the Matlab toolbox PRoNTo (ver2.1.1) (Jessica Schrouff et al., 2013; J. Schrouff et al., 2013) to derive the decoders using SVM (Cristianini & Shawe-Taylor, 2000; Mourao-Miranda, Friston, & Brammer, 2007), and Gaussian Process (Rasmussen, 2003; J. Schrouff et al., 2013). Data was split into two groups; Group 1 included activation maps of the mr_rp task for Dataset 5, and of the vocal_sound stimulus for Dataset 6; Group 2 included the activation maps of the mr_sw, pl_rp, and pl_sw for Dataset 5, and non-vocal_sound for Dataset 6. All maps were input as independent datapoints. We performed a binary classification analysis and used “Binary Support Vector Machine” for SVM, and “Binary Gaussian Process Classifier” for Gaussian process, and constrained the analysis to voxels within the mask created from the second-level group analysis

2.5.2. LASSO-PCR

LASSO-PCR was used to generate decoders following the methods described by Wager et al. (Wager, Atlas, Leotti, & Rilling, 2011; Wager et al., 2013) and was implemented in R. An n×p sparse matrix of subjects (n) and voxels (p) was column-wise centered and scaled. Of note, sparse columns were left sparse since their scaled estimates are undetermined. Principal components analysis (PCA) was performed using singular value decomposition on the column-scaled matrix to obtain a new n×n predictor matrix, X_PCA, and a p×n rotation matrix, R. The reduced predictor matrix, X_PCA, was used in a logistic regression with L₁ regularization (LASSO) (Friedman, Hastie, & Tibshirani, 2010; Simon, Friedman, Hastie, & Tibshirani, 2011; Tibshirani, Johnstone, Hastie, & Efron, 2004). Hyperparameter λ was chosen to minimize binomial deviance using leave-one-out cross-validation across 100 λ’s; default glmnet parameters were used to determine the exact grid range. PCA was performed (and tested) separately within each fold. An n×1 vector of penalized coefficients was pre-multiplied by rotation matrix R to obtain a p×1 vector of voxel weights. This vector of voxel weights served as the decoder.

2.5.3. GLM

GLM was used to generate contrast-based decoders. These simply used the average difference between unsmoothed GLM activity maps (e.g., mean(vocal) – mean(non-vocal)), masked to the same thresholded region as the other decoders.

3. Results

3.1. Overview

Our investigation began with two published pain decoders and one pain encoder that we used as a decoder. Both qualitatively and quantitatively, these decoders were markedly different from one another (Fig 1). Despite these differences, on average, their ability to discriminate pain from non-pain states, using datasets from four published studies (N=113) (Baliki et al., 2009; Liang et al., 2019; Wager et al., 2013; Woo et al., 2015), was nearly identical (Fig 2a). To understand decoding performance’s dependence on decoder spatial properties, we performed several operations to perturb the decoders and reassessed their performance after each modification using the area under the receiver operating characteristic curve (AUC):

Figure 1. Spatial properties for three decoders, which are supposed to distinguish pain from other mental states, are distinct from each other.

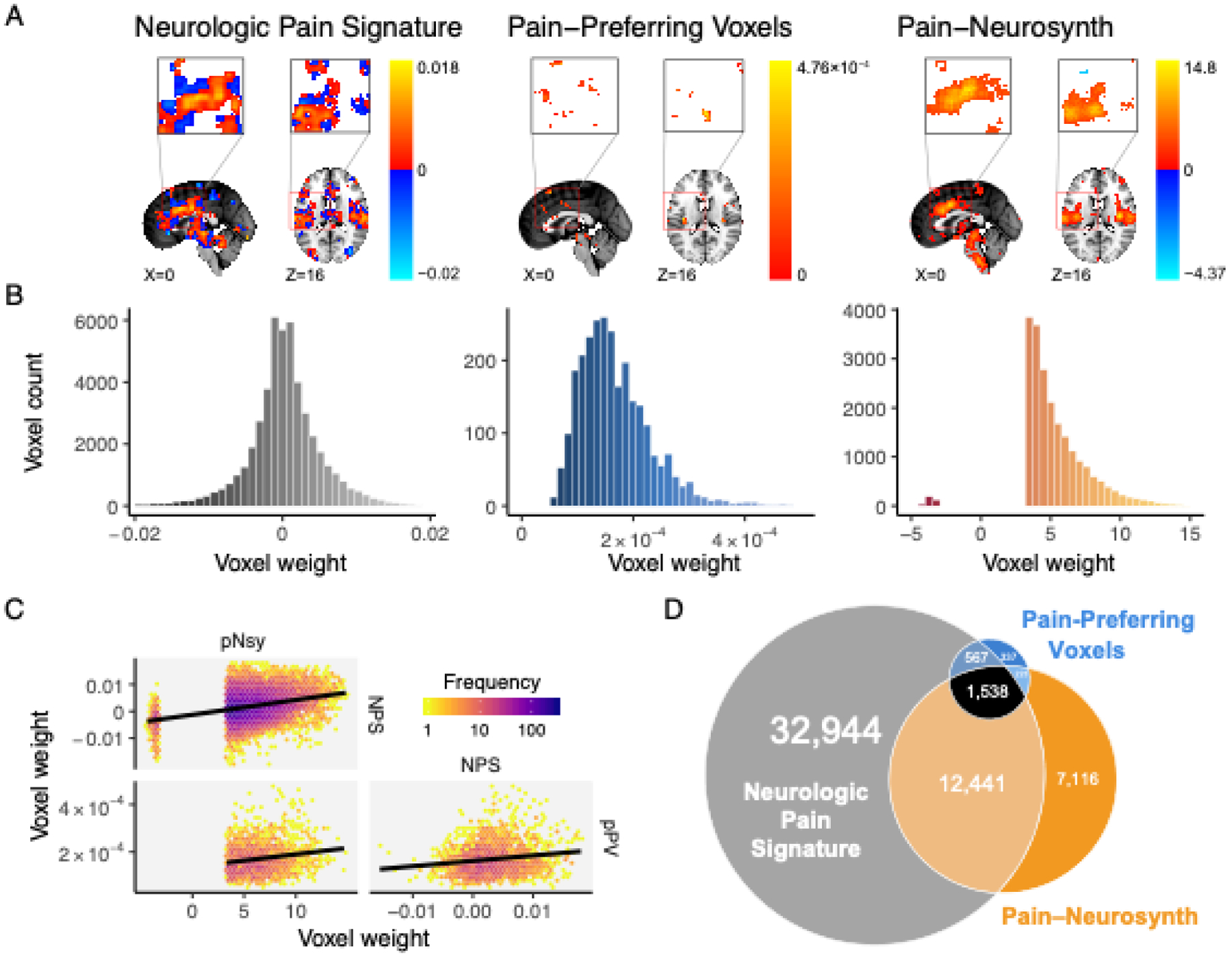
(A) Location and voxel-wise weight patterns of the three pain decoders (respectively abbreviated NPS, pPV, and pNsy). (B) Weight distributions of all three decoders are distinct. NPS weight values are distributed around zero; pPV has no negative weights; pNsy has only a few negative weights. (C) Pairwise correlations between weights of the three decoders. Lines depict total least squares regression fits. All three correlations are weak (r_NPS-pPV = 0.16; r_pNsy-NPS = 0.30; r_pNsy-pPV = 0.18). (D) Euler diagram depicts relative size of each of, and spatial overlap between, the three decoders.

Figure 2. Decoder discrimination performance and regional specificity.

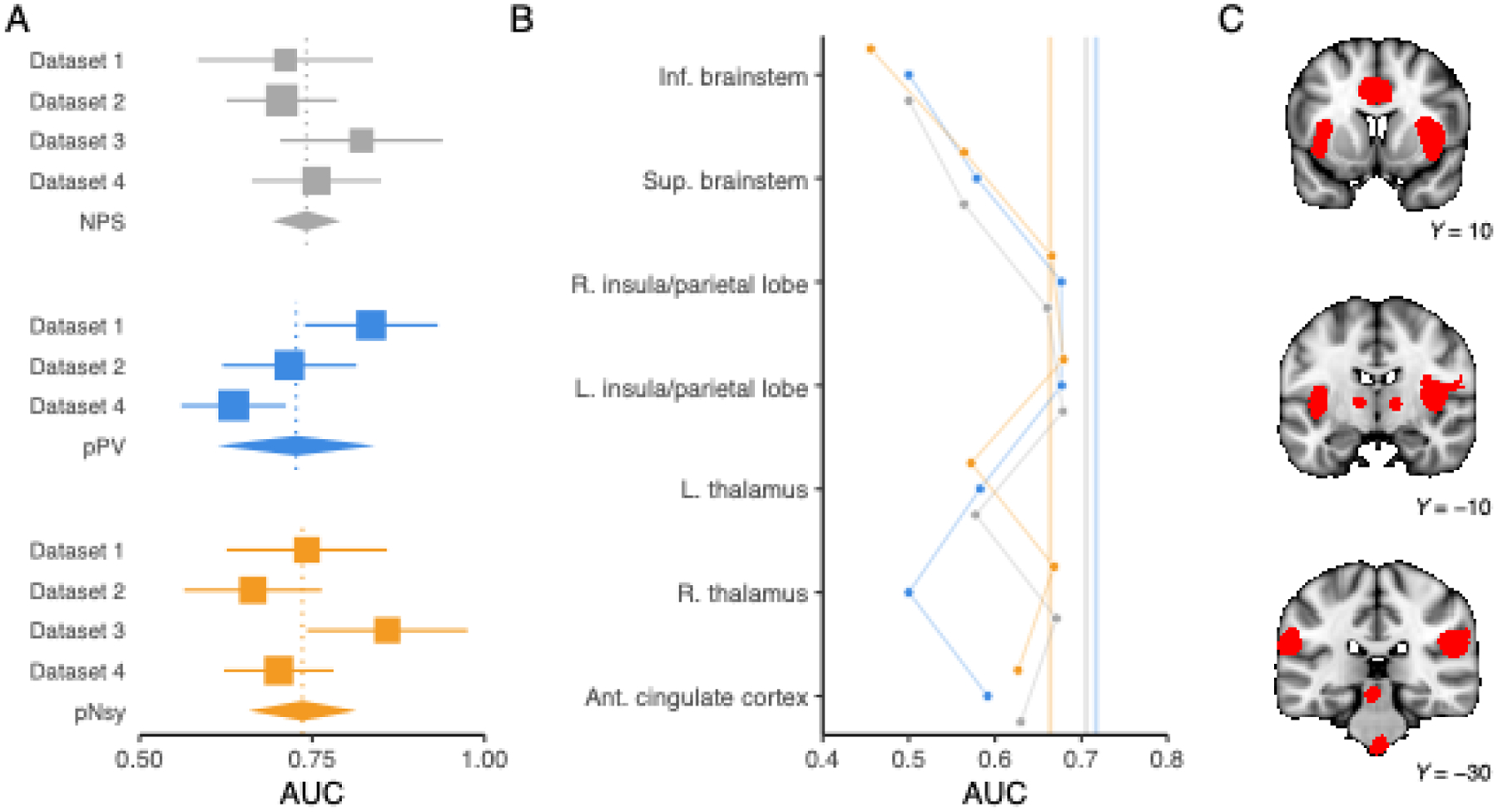
(A) Meta-analysis of across-subject discrimination performance (AUC, chance = 0.5) for decoding pain from non-pain mental states for each of the three decoders. We only included datasets that were independent of decoder derivation; since pPV was trained on Dataset 3, we did not include Dataset 3 in pPV’s meta-analysis. On average, all decoders perform similarly, but there is appreciable variance in each of the estimates. Square sizes indicate meta-analytic weight and lines indicate their 95% CIs. Diamonds are the meta-analytic estimates, and each diamond’s width spans the 95% CI of the meta-analytic estimate. Vertical, dotted lines pass through each meta-analytic point estimate. (B) Regions within each decoder have variable performance. We thresholded pNsy at z=6 to obtain seven contiguous clusters—each of the seven clusters are depicted in red in C. We used these seven clusters as masks for each decoder (see y-axis in B) and evaluated the decoding performance of each decoder within the respective clusters using Dataset 2.(Liang et al., 2019) Full decoder performance is depicted by the translucent vertical lines in B. Grey = NPS; blue = pPV; orange = pNsy. NPS, pPV, and pNsy are published models and were trained on datasets not included in this analysis; all tests are out of sample and cross validation is not applicable.

1. To assess if anatomical regions have differential decoding information, we limited the extent of the decoders to one region at a time. For any given study, multiple clusters from multiple decoders performed similarly well and even matched the performance of the full-brain decoder (Fig 2b–c, Fig S2).

2. To test the influence of the spatial resolutions on performance, we blurred each pattern using a spatial Gaussian filter (Fig 3a, Fig S1). We filtered each decoder within its nonzero voxels using standard deviations ranging from 1–20 mm. In addition, we created a binary map, wherein nonzero voxels within each decoder were set to 1 and all other voxels 0, and a sign decoder, where positive voxels were set to +1, negative voxels −1, and everything else 0. Remarkably, the performances of all three decoders were unaffected by pattern blurring; even the extreme blurring present in the sign templates, and, with some exceptions, the total blurring of the weights in the binary templates did not affect decoding performance (Fig 3b, Fig S3).

3. To test the redundancy of information captured by the nonzero weights within each decoder, we constructed decoders that included only a subset of voxels from the original templates. We randomly sampled nonzero weights, starting with 10 voxels and increasing to the full decoder. Maximum performance of the decoder was realized even using a random selection of just 10% of the decoder’s voxels (Fig 3c, Fig S4–6).

4. To assess the impact that voxel weights have on performance, we built decoders using 10% of the original decoders’ voxels, selected according to their absolute weight percentile (Fig S7). The top 10 percentile, followed by weights between the 80 and 90 percentiles, then between 70 and 80, etc. Performance degradation was present in some but not all decoders and datasets (Fig 3d, Fig S8–9).

Figure 3. Discrimination performance is similar for all three pain decoders and is a function of voxel locations, not weighted patterns.

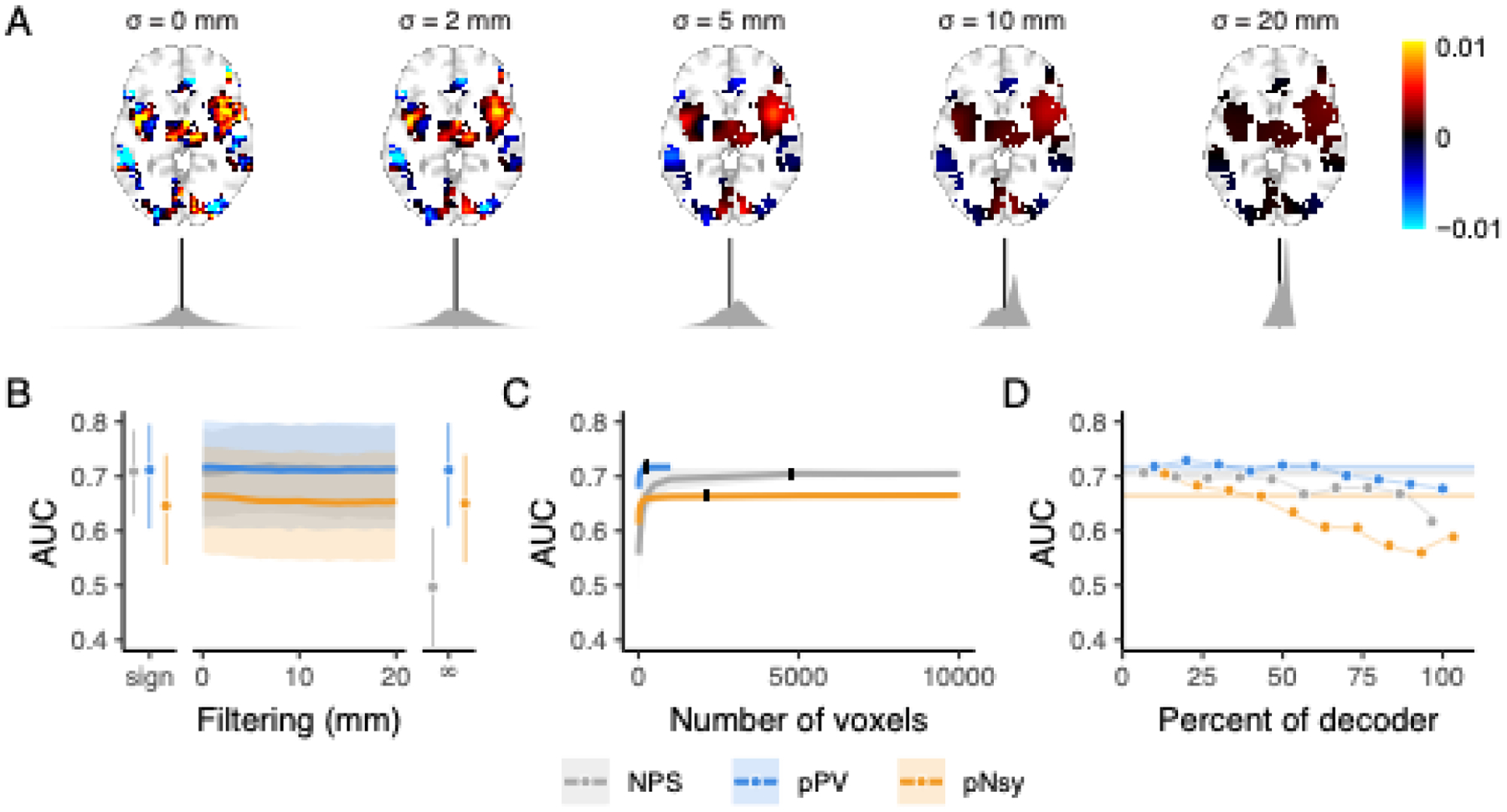
(A) Example of spatial smoothing and its effects on decoder weight distributions. Here, we applied spatial smoothing to NPS with standard deviations of 0 (no smoothing), 2, 5, 10, and 20 mm. Note that smoothing was only applied within the extent of the original decoder (non-zero voxels). The fine-grain pattern observed with no smoothing is quickly destroyed (i.e., already visually by 5 mm smoothing), and at 20 mm of spatial smoothing, the pattern that is left hardly resembles the original decoder. Kernel densities below each brain (grey) are the distributions of voxel weights (black line = 0). With more spatial smoothing, the distributions become more homogeneous and converge toward their mean positive weight. (B-C) Across-subject decoding of pain from touch using Dataset 2 (Liang et al., 2019). (B) Performance does not change when decoder pattern weights were distorted with increasing-size spatial smoothing. Sign = sign of original voxel weights, rendering decoder weights of 0, −1, and +1; filtering σ = 0–20 mm; ∞ = infinite smoothing rendering a binary map. (C) Decoder performance depends only on a very small number of voxels, indicating information redundancy. The number of voxels constituting each decoder was systematically increased (from 10 voxels to the full decoder) and performance assessed for random samples of each size. 10% of each full decoder’s voxel count (black ticks) discriminates pain from touch equivalently to the full decoders. Shades are standard deviations for spatial uncertainty, ignoring across-subject uncertainty. (D) Decoders were constructed using 10% of the voxels from the full decoders, with voxels selected in order of their absolute magnitude, where 0 is the highest magnitude voxels and 100 is the lowest (see Fig S7). The voxels with the highest absolute weights do not necessarily discriminate better than voxels with lower magnitudes, except for pNsy in this dataset. Bars and shades are the 95% confidence intervals [CI] of AUCs, except in C, where shades indicate standard deviations associated with permutation variability. In D, colored bars indicate the AUC of the full decoders. NPS, pPV, and pNsy are published models and were trained on datasets not included in this analysis; all tests are out of sample and cross validation is not applicable.

We generalized our findings by examining the decoders for cognitive domains other than pain, where functional segregation is better established; namely, a reading task and a listening task (two publicly available datasets, n=14 and n=213 subjects, respectively) (Jimura, Cazalis, Stover, & Poldrack, 2014b; C. R. Pernet et al., 2015). We compared decoding performance between encoders used for decoding (GLM) and decoders, before and after constraining the decoders to binary or signed maps. Our results closely resembled those for decoding pain (Fig 5).

Figure 5. Different implementations of cognitive and auditory decoders perform similarly regarding discrimination performance and are robust to perturbations.

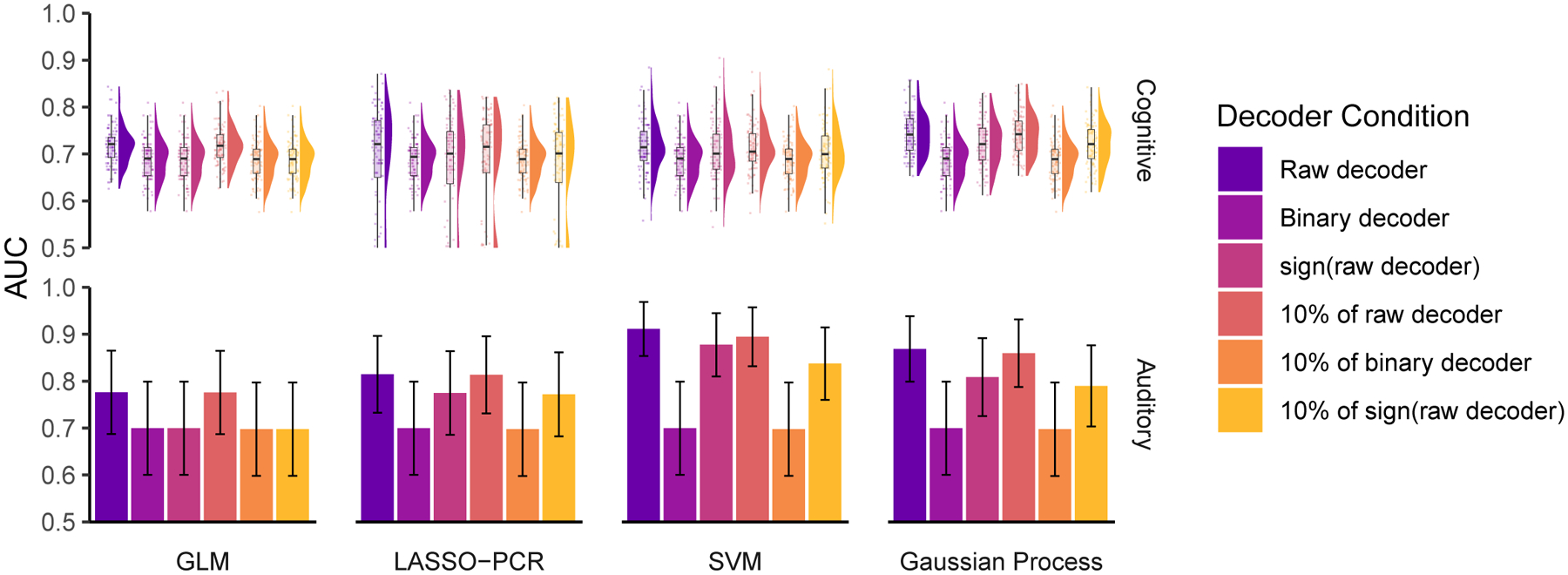
We constructed decoders using general linear modeling (GLM), least absolute shrinkage and selection operating with principal components regression (LASSO-PCR), support vector machines (SVM), and Gaussian processes to decode (top) cognitive (reading mirror txt after mirror text vs mirror-plain, plain-plain, and plain-mirror) (Jimura et al., 2014b) and (bottom) auditory tasks (listening to vocal vs non-vocal sounds) (C. R. Pernet et al., 2015). Much like the pain decoders, these decoders performed similarly and better than chance (chance = 0.5 in both) and were relatively insensitive to perturbations. Just 10% of each decoder was enough to capture its full performance, and even extreme perturbations, such as 10% of the binary decoder or 10% of sign(decoder), had little effect on performance. Error bars are the 95% confidence intervals of the AUCs. For the cognitive task analysis, we estimated the distribution of AUC using 100 permutations of randomly splitting the subjects in half, used one half for training and the second for validation. In the auditory task analysis, the large number of subjects (213) allowed us to split the sample into a training group (107 subjects) and a testing group (106 subjects) without a need for permutations.

The brain imaging literature commonly accepts that if a decoder can adequately discriminate between a decodee and a comparator, then it may also be useful for identifying the mental state associated with the decodee. We tested this concept for both pain and listening tasks. Despite discrimination being possible and robust to perturbations, all decoders performed poorly and relatively similarly when trying to identify the decodee mental state (Fig 6).

Figure 6. Identification of mental states shows poor predictability.

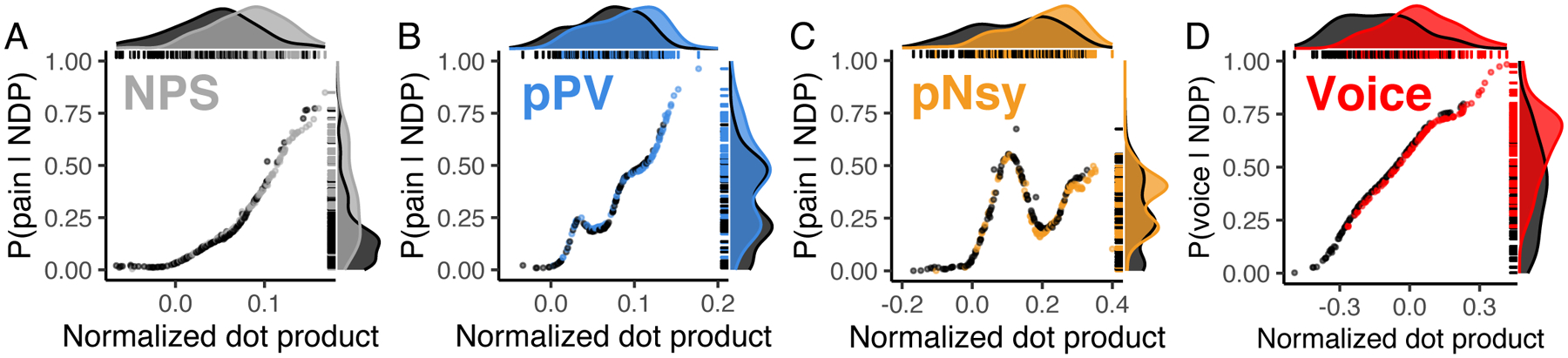
Three pain decoders (NPS, pPV, and pNsy in A–C) and a voice decoder (D) were used to test identification for mental states. x-axes are the normalized dot products between decoder and decodee, while y-axes are the posterior probability of being in pain (A–C) or listening to voices (D). Distributions of normalized dot products and posterior probabilities include both the decodee (light grey & colors) and comparator (dark grey) tasks. (A–C) Normalized dot products of the pain condition span the entire distribution of comparator normalized dot products, and as a result, pain is not adequately isolated from the comparator conditions. Quantitatively, this is evidenced by the strong decodee-comparator overlap for (A) NPS (overlap (95%CI) = 68% (59–82)), (B) pPV (79% (73–90)), and (C) pNsy (73% (66–84)). This is reflected in the Bayesian model, which shows similar probabilities of being in pain for both pain and pain-free conditions (each dot/line). To this end, all three decoders perform similarly, and cannot unequivocally identify pain, as indicated by their sensitivity/specificity (threshold from Youden’s J statistic, chosen in-sample) of (NPS, A) 0.64/0.74, (pPV, B) 0.6/0.64, and (pNsy, C) 0.54/0.76. (D) In contrast to pain, a contrast map decoder for identifying when a participant is listening to human voices separates more clearly the normalized dot products of the decodee (red) from comparator (dark grey), but still performs poorly (overlap = 54% (46–66)). This separation is reflected in the Bayesian model, which shows high probabilities when individuals are listening to human voices and lower probabilities when they are not. Using a threshold determined by Youden’s J statistic (chosen in-sample), the voice decoder has a sensitivity/specificity of 0.77/0.64. In (A), (B), (C) the dataset used were not used in the training of the decoders (NPS, pPV, pNsy); tests are all out of sample. In (D), we split the dataset into a training set (107 subjects) and a testing set (106 subjects).

The results of our perturbation analyses led us to explore the limits of decoding. If perturbed and simplified decoders can perform similarly to the original decoders, can we further simplify decoders and explain decodability? To address the former question, we built pain decoders using noxious stimuli encoders (brain activity maps). These encoding models performed similarly to decoders. Unsurprisingly, within-study performance was slightly superior to across-study performance (Fig 7a–b). We extended these findings to quantify within- and across-subject decoding using four different tasks (mr-mr, mr-pl, pl-pl, pl-mr), repeated up to 12 times per subject in 14 subjects.(Jimura et al., 2014b) This study design provides the opportunity to calculate discriminability as a function of similarity measures from the decoder, decodee, and comparator, for both within- and across-subject decoding. Although performance was not consistently better for within-subject discrimination, variation in performance could be largely explained by within-task homogeneity and between-task heterogeneity, allowing us to propose decoding rules (Fig 7c–d), which worked better for explaining within- compared to between-subject discriminability. These results present convergent evidence that 1) specifically for across-subject discrimination, decoding is limited by the information contained within encoding models (brain activity maps). In particular, sparse, binarized brain activity maps contain sufficient information to discriminate between mental states; 2) identifying a mental state (i.e., no direct comparison) is harder than discriminating between mental states (i.e., a direct comparison); 3) similarity measures almost fully account for the variance of within-subject discrimination performance, which degrades in across-subject discrimination.

Figure 7. Decoders constructed from activity maps (encoders) perform similarly to pattern-based decoders and are dependent on both decodee and comparator properties.

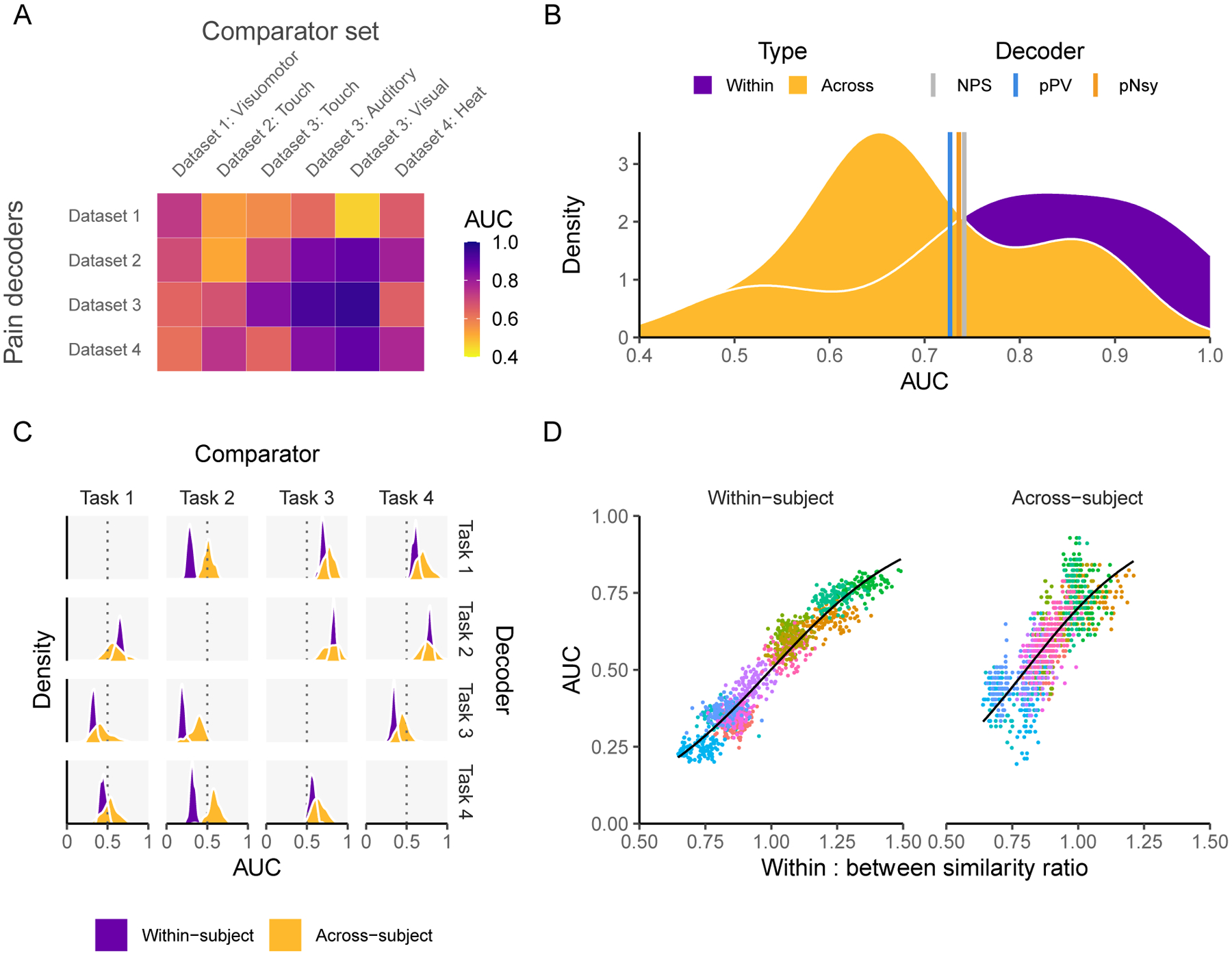
(A) Performance of four activity map decoders, based on the across-subject averaging for pain tasks, to differentiate pain from six other mental states. (B) Among the activity map decoders, within study performance is slightly higher but extensively overlaps with across study performance. Meta-analytic estimates of performance for NPS, pPV, and pNsy (color lines) are within 0.4 standard deviations from the average performance of both within and across study activity map decoders. (C-D) Properties of activity map decoders are examined within and across subjects as a function of a cognitive task (mr-mr, mr-pl, pl-pl, pl-mr) (Jimura et al., 2014b). (C) Decoders (rows) are built from four cognitive tasks, tested on remaining three (columns), in a within subject and across subject design. Within subject performance is always more consistent (i.e. it has smaller variance) but not necessarily greater than across subject. For example, the within subject performance is always superior to across subject when using task 2 as the decoder. The inverse is true when task 2 is the comparator, implying strong task dependence. (D) Decoder performance scales with the ratio of decodee similarity to decodee-comparator similarity (based on normalized dot product), for within- and across-subject comparisons. Because discriminability depends on this ratio of similarities, they can be viewed as rules for decoding. Each color in (D) represents a decodee-comparator pair of tasks 1–4 in (C); each point is a permuted sample that has been shrunken towards 0.5; the black line is the fit of a beta regression (Cribari-Neto & Zeileis, 2010) across decodee-comparator pairs. In (A) the testing is a combination of within sample (also within study) for the case of: Dataset 1 – Dataset 1: Visuomotor, Dataset 2 – Dataset 2: Touch, Dataset 3 – Dataset 3: Auditory, Dataset 3 – Dataset 3: Visual, Dataset 4 – Dataset 4: Heat, and out-of-sample for all other combinations. In (C) the results are calculated using 100 permutations of randomly splitting the subjects in half, used one half for training and the second for validation.

3.2. Exploring established decoders

We started by assessing the similarities and differences of three pain decoders. Two of them are optimized multivariable decoders: The Neurologic Pan Signature(Wager et al., 2013) (NPS), constructed using LASSO-PCR, and the Pain-Preferring Voxels(Liang et al., 2019) (pPV), constructed using SVM. The third decoder is an encoder: the meta-analytic association map from Neurosynth (Yarkoni et al., 2011) for the term “Pain” (pNsy). pNsy is a mass-univariate map based on reported statistically significant coordinates from 516 pain-related studies contrasted with the remaining 13,855 studies in the Neurosynth database. Spatially, the three decoders include voxels from approximately the same brain regions (Fig 1A), with some but not full overlap (Fig 1D). They have substantially different numbers of voxels and distinct voxel weight distributions (Fig 1B): pPV and pNsy have 2,665 and 21,318 voxels, respectively, all with positive weights, except for a few negatives in pNsy, whereas NPS has 47,590 voxels with weights distributed around zero. In addition, the correlations between the weights of voxels common in any two decoders are weak (r = 0.17–0.30; Fig 1C).

3.3. Discrimination performance for pain is similar between diverse decoders

We used the three decoders to discriminate between painful and non-painful control stimuli in data from four published studies, collected from three labs, totaling 113 subjects. Discrimination was based on a similarity measure—normalized dot product (NDP), also known as cosine similarity—between an encoding of the stimulus (brain activity map) and the decoder. Others have used NDP for decoding; e.g., the application of NPS to neonatal and adult brain responses to noxious stimuli (Geuter et al., 2020). Much like a correlation coefficient, NDP produces +1 for identical patterns, 0 for orthogonal patterns, and −1 for opposite patterns; however, NDP does not demean the patterns, in turn preserving negative voxel weights and “deactivations”. The assumption was that a pain decoder should be more similar to an encoding of pain (decodee brain activity map) than an encoding of a control task (comparator brain activity map). We used AUC as an indicator of discriminability since it can be interpreted as the probability of a randomly sampled decodee NDP being greater than a randomly sampled comparator NDP, implying a direct comparison. We meta-analyzed the performance of each decoder across datasets (except for pPV and Dataset 3, which was used for its development; Fig 2a). Decoding performance showed dataset-dependent AUCs. However, the meta-analytic estimate for each decoder was similar (AUC ≈ 0.73).

This average performance similarity is remarkable and informative about the nature of what drives decodabiltiy; it implies that different models may nonetheless yield similar average performance, indicating that their detailed properties do not constrain decodability. Notwithstanding similar average performance, the decoders performed differently across datasets, indicating that decoding performance also has a specificity component which can likely be explained by brain region-specific dependencies.

3.4. No single brain region is necessary for decoding

We investigated brain region-dependence within the pain decoders. To do so, we first divided each decoder into seven parts based on seven different brain regions (Fig 2c; see Methods for details). Next, we evaluated the decoding performance within each region for discriminating painful from non-painful stimuli for datasets 1–4. Multiple clusters from multiple decoders performed similarly well and matched the performance of the full decoder (Fig 2B and Fig S2). Moreover, some clusters in isolation showed superior point estimates to the entire decoder, but this was not generalizable across studies and decoders. For instance, the voxels from NPS in the right insula had an AUC greater than that of the full decoder when discriminating pain from touch in Dataset 3, but lower when discriminating the same stimuli in Dataset 2. In some instances, such as the inferior brainstem in NPS and pPV and right thalamus in pPV, the clusters had no spatial overlap with the decoders. For these cases, the performance yielded an AUC of 0.5. The inferior brainstem consistently performed worst across studies and decoders. This is partially explained by the exclusion of the inferior brainstem from NPS and pPV. However, in pNsy, we suspect this effect is due to the influence of physiological noise that contaminates brainstem activity. These results suggest that no anatomical region has greater pain decoding power than other regions.

3.5. All Three pain decoders are insensitive to spatial perturbations

3.5.1. Spatial smoothing of voxel weights

To investigate whether discrimination performance relies on the high resolution fixed-weight nature of the decoder’s voxel patterns, we measured performance when these patterns were degraded by spatial smoothing of the decoder weights using a Gaussian filter with increasing width, up to 20 mm and ‘infinite’ smoothing (Fig 3A, Fig S1). Gaussian filtering removes the high-frequency content from the decoder pattern, effectively reducing the resolution; the wider the filter kernel is, the lower the resulting resolution. Of note, this spatial smoothing yields decoders with cutoff frequencies below that of the activation maps. We also built a binarized version of each decoder wherein all voxels within a decoder were assigned a value of 1 and all voxels outside the decoder are zero, effectively destroying all high-resolution information within the decoder. The binarized decoder emulates an infinitely filtered decoder. We also built a “sign” version of each decoder, where positive voxels become +1, negative voxels −1, and everything else 0. Remarkably, decoding performance was minimally affected by these procedures, with performance dropping to chance level only for the binary version of NPS in Dataset 2 and a slight downward trend also for NPS in Dataset 4 (Fig 3B, Fig. S3). This result clearly demonstrates that the fine-grained pattern of weights in these decoders added no value to performance (with a few exceptions, Fig S3).

3.5.2. Number of voxels

To characterize the minimum number of voxels necessary to discriminate the pain from non-pain states, we created sets of new decoders by randomly selecting subsets of voxels from each decoder. Our analysis spanned from 10 voxels up to the full decoder. Surprisingly, we attained the original decoding performance when only using a random 10% of the total number of each decoder’s constituent voxels (Fig 3C). We replicated this finding on all datasets and for all three decoders, using their original form (Fig S4), when using their binarized versions (Fig. S5), and when using their sign versions (Fig S6).

3.5.3. Significance of voxel weights

We further explored the relationship between voxel weights and performance. Particularly, we wanted to investigate if voxels with higher weights (e.g., the top 10%) are more specific to pain and will yield greater AUCs than those voxels with lower weights (e.g., the bottom 10%). For each decoder, we binned voxels by their absolute weights and then constructed a set of decoders using the voxels in each bin (see Fig S7). We generated decoders using 1%, 5%, 10%, and 20% bins. For example, the 10% binned decoders are a series of decoders where the first decoder includes the top 10% of the voxels according to the absolute value of their weight, the second decoder is made up of the second 10%, etc., and the last of the series is a decoder that is made up of the bottom 10% of the voxels. Two versions of each series were generated: one version where we left the voxel weights intact and a second where we binarized the decoders after binning. Again, we observed only minimal degradations in performance with decreasing voxel weights for all decoder-dataset combinations (Fig 3D). Degradations were primarily seen for pNsy in Dataset 2 (painful heat vs. touch), and NPS in Dataset 3 (pain vs. auditory and pain vs. visual) (Figs. S8–S9).

3.5.4. Pattern value in stimulus/perception intensity decoding

Fixed-weight, multi-voxel pattern decoders derived with machine learning have been used to model stimulus and perceptual intensities. For example, in addition to binary classification of heat stimuli of different intensities, Wager et al. (2013) (see also (Tu, Tan, Bai, Hung, & Zhang, 2016)) used NPS to capture stimulus intensity and perceptual ratings from brain activity. To this end, we tested the ability of the three pain decoders to capture stimulus and perception properties. We used data from a study where nonpainful and painful stimuli of different intensities, perceptual responses, and their associated brain activity were available.(Wager et al., 2013) All three decoders (NPS, pPV, and pNsy), whether raw or binarized, performed similarly for capturing perceived pain ratings (Fig 4A,B), for reflecting the intensity of the thermal stimulus (Fig 4C,D), and for discriminating between pairs of painful stimuli (Fig 4E,F). We performed this analysis using both NDP and dot product (DP) as outcome measures. The latter was used in the original study and provides opportunity to compare the present results to the original study. The results of the DP better match the original study. The discordant performance between NDP (nonmonotonic, Fig 4A, C, and E) and DP (almost monotonic, Fig 4B, D, and F) suggests that previously reported results (Wager et al., 2013) are attributable to an increase in the magnitude of brain activity in specific regions, but in a way that becomes less similar to the decoder as indicated by the nonmonotonic trend of NDPs. Yet, both NDP and DP were insensitive to the removal of voxel weights.

Figure 4. All three pain decoders perform stimulus-perception mapping similarly, both in their original formulations and after replacing voxel weights by binary representation (0,1 values).

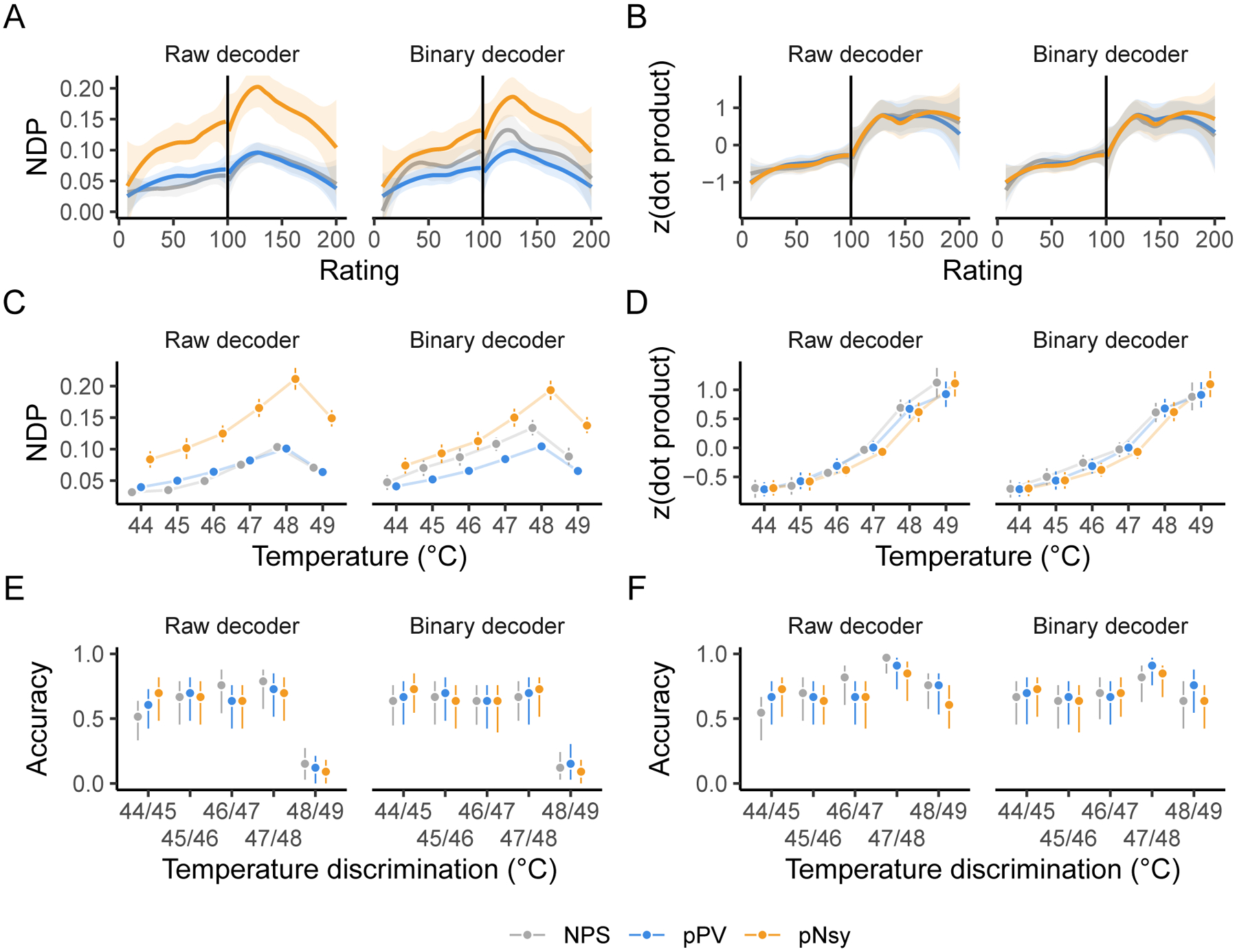
When binary decoders are compared to the unfiltered (or raw) decoders, all three pain decoders perform similarly in mapping pain and heat perception ratings (A–B), mapping painful stimuli (C–D), and discriminating between pairs of painful stimuli (E–F). Analysis was done using both normalized dot product (NDP) and dot product since NDP produced results discordant with an original publication(Wager et al., 2013) that relied on dot products. Dot products that do not reliably increase with increasing pain or temperature imply that the decoders cannot reliably predict subjective ratings or stimulus intensity. Vertical lines in A and B indicate the transition from nonpainful heat (< 100) to painful heat (> 100). The dot products in B, D, and F were z-scored within each decoder for presentation purposes. NPS, pPV, and pNsy are published models and were trained on datasets not included in this analysis; all tests are out of sample and cross validation is not applicable.

Our results show, at least for the stimuli and decoders we have analyzed, that optimized decoders (NPS, pPV) offer no advantage over the simpler, mass-univariate encoder that is used as a decoder (pNsy) for binary classification and stimulus-perception mapping. Additionally, the voxel weights in these decoders seem to provide little decoding advantage. This reinforces the notion that binarized decoders perform sufficiently and that useful information is provided only by the decodee activity in a small subset of the locations where a decoder has non-zero weights.

3.6. Cognitive and auditory decoders are similarly highly redundant

So far, we have shown that popular pain decoders, as well as a meta-contrast map (encoder) used as a decoder, are able to maintain their full performance after being perturbed and degraded, indicating that much of the information contained within them is redundant. One worries that the findings may be specific to the modality studied, as pain and nociception are sensory systems for which no dedicated tissue has been uncovered in the neocortex (Chen, 2018). As a result, there is long-standing debate as to specific or distributed encoding of pain perception (e.g., (Segerdahl, Mezue, Okell, Farrar, & Tracey, 2015); cf. (Iannetti & Mouraux, 2010; Petre et al., 2020)). To broaden our findings, we examined whether the uncovered principles apply to decoding for audition and reading. Primary and secondary auditory cortex (Brewer & Barton, 2016; Fruhholz & Grandjean, 2013) are in close proximity to the somatosensory regions examined above for pain and cortical columns in the region reflect specific auditory properties, while language representation with dedicated and functionally specific tissue is unique to humans (Broca, 1861). We used data from reading (Jimura et al., 2014b) and auditory (C. R. Pernet et al., 2015) studies to construct encoders using contrast maps, as well as decoders using multivariable SVM, LASSO-PCR, and Gaussian processes (our contrast maps closely resemble those reported in the original studies, Fig S10–S11; see Methods). In the case of the reading cognitive task, our findings are entirely concordant with those for the pain decoders: all the constructed decoders show similar performance, which was maintained after extreme perturbations (e.g., sign or binary decoder) (Fig 5). These findings generalize and provide compelling support for our main result: decoders are highly redundant, and decoding primarily exploits information contained within voxel locations, independent of voxel weights. Moreover, task-specific encoders (contrast maps) are sufficient for decoding, implying that the meta-contrast maps (e.g., from Neurosynth) are also not necessary.

In the auditory task, discrimination performance is better with LASSO-PCR, SVM, and Gaussian Process than with GLM. We suspect these differences are a consequence of specific instantiations of overfitting or due to the larger sample size enabling the models to capture more encoding detail. We observed similar decoder-dependent performance variations for the pain decoders as well (see Fig 2A); yet, in further analyses, none showed superiority over the others. In the auditory task, and for both SVM and Gaussian Process decoders, we also observed appreciable performance decrement for binary maps and for 10% binary map decoders. This too was observed in the pain decoders. Like with the pain decoders, here, we also observed that binary map decoders and 10% of sign(decoders) performed similarly to the raw decoders, again suggesting that negative weights at large scales can influence decoder performance.

3.7. Identification remains a challenge

The ability of machine learning-derived decoders to identify mental states is repeatedly asserted in the literature (Eisenbarth et al., 2016; Kragel et al., 2018; Lindquist et al., 2017; Marquand et al., 2010; Poldrack et al., 2009; Wager et al., 2013; Wager et al., 2015; Woo et al., 2015). If decoders are used with the objective of identification, then they should be able to pinpoint the specific mental state solely from the similarity between the decoder and decodee, and, crucially, in the absence of a comparator. This is akin to being able to state whether a dog is a pug without other dogs being present. In other words, identification should be based on a single observation and what we (or the decoder) “know(s)” about the world. This may involve a set of brain responses to any possible stimulus—a very large set. Alternatively, discrimination only requires information about two brain states: the decodee and the comparator. Therefore, instead of AUC, which implies a comparison, we tested identifiability by calculating distributional overlap between the states of interest and no interest. Distributional overlap estimates the proportion of points that have an equal probability of belonging to the state of interest and state or states of no interest; here, equiprobability implies unidentifiability. In other words, the proportion of points that are unidentifiable. In addition, we were interested in assessing performance at the individual level. To do so, we calculated the probability of a subject being in a specific mental state given that subject’s brain activity map. Distributional overlaps and state probabilities assessed the ability of decoders to identify mental states.

Identification of pain states was similarly poor across the three pain decoders explored: overlaps between states of interest and states of no interest were high (≥ 68%) and the probabilities of being in pain (when actually in pain) were low (median posterior probability ≤ 0.5) (Fig 6a–c). These results paint a markedly different picture than the discrimination results, which simply show that NDPs tend to be greater when individuals are in pain. Evidently, good discrimination does not imply good identification.

We built upon the pain findings by using the task-specific contrast map to decode perception of vocal versus non-vocal sounds (C. R. Pernet et al., 2015). Although the performance of the voice decoder was better than that of the pain decoders (overlap = 54%), it was still inadequate, as over half of the data was unidentifiable (Fig 6d). The slight superiority of the voice decoder relative to the pain decoders may have several explanations, including the homogeneity of the training and test sets used for the voice data or simply that some tasks are easier to identify than others. In any case, regardless of the mental state tested, identification remained unreliable and thus does not seem currently feasible with fixed-weight decoders.

3.8. Brain activity maps are sufficient for discrimination

The similarity in performance achieved by meta-contrast maps or task-specific contrast maps (encoders) and optimized multivariable decoders prompted us to take another step back in the decoding derivation process. Would an even simpler construct—pain activity maps—be sufficient to decode the state of being in pain? In other words, if no performance is lost by using contrast maps, would task-derived activity maps suffice as simpler but adequate decoders? We created brain activity map decoders by averaging half of the brain activity maps for each study’s pain task, leaving the remaining maps for testing. Each activity map decoder was then used to discriminate pain using the left-out brain activity maps of subjects both within and between studies (Fig 7A). Remarkably, these decoders performed comparably to the ones presented hitherto (NPS, pPV, and pNsy), with an average within-study AUC of 0.79 and between-study AUC of 0.69 (cf. ~0.73 for the fixed-weight decoders; Fig 7B). Combined with our earlier findings, these results raise a salient question: If decoding can be approached in so many different ways, what actually determines decodability?

3.9. Modeling decodability

Although decoding is difficult, decoding performance itself is likely predictable; yet, to our knowledge, remains unexplored. To build upon our breed metaphor, some dogs exhibit features that largely overlap with other dogs, such as the stature, color, and flat-faced features of pugs and French Bulldogs. Similarly, the mental state of “being in pain” shares many features with other states; for example, unpleasantness, behavioral relevance, and saliency (Mouraux & Iannetti, 2018). Therefore, the primary challenge of decoding is to tease apart these overlapping features. For this reason, it seems logical that the similarity of activity maps within and between the decoder, decodee, and comparator would determine decoding performance. If the decoder is built from activity maps that are dissimilar, the resulting average map would have a low signal-to-noise ratio; if the decodees or comparators are dissimilar, then we can expect a greater variance in NDPs; and if the decodees and comparators are similar to one another, then they will have high overlap and be difficult to tease apart. This logic implicates the neuroanatomical and physiological assumptions previously mentioned, as heterogeneity across individuals should decrease similarity, making the NDPs more variable and thus more difficult to discern. Using similarity metrics that reflect these relationships, we attempted to explain decodability.

Until now, we have primarily focused on decoding across- rather than within-subjects. Intuitively, it is apparent that, for many of the reasons elaborated above, decoding mental states should be more successful within-subjects compared to across-subjects, as has been formulated by others (Cox & Savoy, 2003; Haxby et al., 2011). However, no systematic analysis of this notion has been performed using fixed-weight decoders. Therefore, we investigated this question using data well-suited for the question: fMRI data collected from 14 subjects who completed four cognitive tasks, each with 12 replicates (Jimura et al., 2014b). These repetitions enabled the comparison of decoder performance within- and across-subjects. As expected, decoding performance is more precise (smaller variance) within-subject (Fig 7C), but interestingly, not necessarily better (greater average AUC). We investigated whether the ratio of decodee to decodee-comparator similarity (or within:between) can be a possible natural metric of why some decoders are more efficacious than others. This ratio was calculated as the average NDP of all 15 decodee pairs divided by the average NDP of all 36 decodee-comparator pairs. Higher performing decoders showed greater within:between ratios than lower performing decoders (Fig 7D). Similarly, decoder similarity—the average NDP of all pairwise combinations of a decoder’s constituent activity maps, a measure of reliability—could also explain much of the decoder performance, and in support of our previous conclusions, this relationship is largely unaffected by binarizing the decoder (Fig S12). Further exploration showed that decodability, especially within-subject, is strongly predicated on these similarity metrics (Fig S13–S14; Table S1). Decodee similarity, together with decodee-comparator similarity, is strongly predictive of discriminability, accounting for 91% the variance in AUCs. Our similarity metrics almost entirely explain within-subject decodability, but only about 62% of AUC variance in across-subject decoding. This result may speak to the assumptions violated by across-subject decoders, in that a similarity score across-subjects is less interpretable than one calculated within a single subject since variance (e.g., brain anatomy) may be converted to bias (making all brains fit the same template) during image preprocessing and registration.

4. Discussion

In this study, we asked what the determinants and limits of decoding mental states are. For pain, reading, and language tasks, only the locations of a small subset of GLM-derived voxels from an encoder were sufficient for achieving a discrimination of AUC ≈ 75%, and a long list of machine learning tools could not consistently improve upon this performance. We also showed that, in contrast to discriminating between states, identification of a given perceptual state is much harder. For the first time, we advanced the concept of quantifying discriminability using a simple similarity metric, the NDP, with which we provide models for within- and across-subject discrimination. The latter analyses indicated that discriminability depends not only on the decoder, but also on similarity between the decodee and comparator. Finally, we showed that, even in an example where within-subject discrimination was almost fully modeled with similarity properties, there was a considerable decrease in the variance of across-subject discrimination that could be explained. In doing so, we establish limits of decodability based on fixed-weight models currently used in fMRI literature.

Our similarity metrics explained a large proportion of the variance in AUCs both within- (95%) and across- (68%) subjects. The within:between similarity metric in particular—which is calculated as the average decodee similarity divided by the average decodee-comparator similarity—is conceptually similar to reliability. If the decodee is not reliable, it will have a low average decodee similarity; if the decodee and comparator share a lot of variance, the decodee-comparator similarity will be high. To successfully decode, the decodees must be similar relative to the comparator. Reliability assesses a similar construct: variance must be low within a subject (or task) relative to between subjects (or tasks). Thus, the reliability of fMRI itself must be considered when trying to understand decoders. fMRI’s reliability has been scrutinized for some time,(Vul, Harris, Winkielman, & Pashler, 2009) and recently, Elliott et al. (2020) carried out a meta-analysis demonstrating fMRI’s poor reliability (e.g., task-fMRI intraclass correlation coefficient [ICC] < 0.4). However, as astutely noted by Kragel, Han, Kraynak, Gianaros, and Wager (2021), how the ICC is calculated matters. For multivoxel-based decoding (e.g., with multivariable models), multivariate ICCs are of greater interest and exceed 0.75. From a data quality viewpoint, our similarity metrics imply that designing experiments that maximize task reliability should enhance decodability—it is prudent that such measurement properties be considered before collecting data.

Limitations of across-subject decoding and reverse inference have been acknowledged by others. For example, recent evidence shows that brain-behavioral phenotype associations seem to become reproducible only with sample sizes of N ⪆ 2,000.(Marek et al., 2020) Yet, the extent of these limitations and specifically the spatially widespread redundancy of fixed-weight decoders has not been previously quantified, nor has decodability been modeled. Multiple approaches have been adopted to overcome such limitations. The simplest is to avoid these complications by constraining fMRI studies to within-subject investigations, thus bypassing the idiosyncrasies of anatomically aligned group-averaged results. The approach obviates across-subject decoding, yet it is used by various groups, including subject-specific localizers in vision (Nasr, Polimeni, & Tootell, 2016) and language studies (Fedorenko & Blank, 2020). An alternative solution is to build task-based brain atlases using a large number of tasks, preferably in large numbers of subjects (e.g. (Nakai & Nishimoto, 2020; Pinho et al., 2020)), which may be used as priors in future specific studies.

On the other hand, multiple approaches have been implemented for decoding mental states from fMRI data (see Supplemental Discussion). Overall, it seems our findings generalize: decoding success is not predicated on voxel-wise specificity. Instead, the information necessary for decoding appears to be spatially coarse and distributed, rendering many voxels contained within the decoders to be redundant. This is not to say that specific voxels are not sufficient for decoding; rather, widespread information sharing across the brain simply enables statistical prediction to occur on a coarse spatial scale. The importance of a fine-grained pattern in a decoder must therefore be explicitly demonstrated (see Recommendations).

Our demonstration that decoders fit using machine learning algorithms do not yield better decoding performance compared to linear encoders is novel but perhaps unsurprising. The decoders themselves were constrained to “statistically significant” encoding voxels; univariately, these voxels were redundant. Although decoders should take advantage of multidimensional information that may not be present in the encoders, tuning voxel weights using multivariable decoding models only slightly improved performance for the voice data (Fig 5, bottom) and had no appreciable effect at all for all other datasets. This overlaps with but differs slightly from what has been observed in both neuroscience(Schulz et al., 2020) and other domains, such as medicine(Christodoulou et al., 2019; Desai, Wang, Vaduganathan, Evers, & Schneeweiss, 2020): simple statistical models, such as logistic regression, on average perform similarly to models fit using machine learning algorithms and we have yet to maximize the performance of parsimonious models. The reasons for this are manifold, and from a modeling viewpoint, it has been argued that the added value of linear “machine learning” techniques is often small, exaggerated, and does not translate into practical advantages,(Hand, 2006) in part due to small training samples.(Schulz et al., 2020) Our data take this idea a step further by demonstrating that encoders—which are essentially t-test parameters—contain sufficient information for decoding. It may be the case that full-brain decoders that are not constrained by contrast maps perform superiorly, but preliminary evidence suggests performance gains may be marginal.(Zhou et al., 2020) Further, the large number of predictors relative to the small sample sizes yield statistically indeterminate models, meaning infinite models exist for a given stimulus. Although unsurprising given the aforementioned work in this area, the apparent stark discrepancy between our findings and those in the literature warrants explicit explanation.

How do we explain the discrepancy between our results and the literature, even when the same decoder is used on the same data (Wager et al., 2013)? We cannot escape the conclusion that decoders are superfluous models. Indeed, Wager and colleagues have also observed similar performance across several pain decoders, including NPS, pNsy, and a candidate NPS model that used SVM.(Geuter et al., 2020; Wager et al., 2013) Yet, across-subject decodability remains complex; only brain location seems to add value, and decodability depends on within and between similarity of decoder, decodee, and comparator. These findings advance the general principles of decoding mental states.

5. Recommendations

Importantly, the results of our study provide valuable insight for the field of decoding and several practical takeaways that can improve the future efforts in creating fixed-pattern decoders. Specifically, we suggest that authors include and consider the following:

1. Perturbations of the decoders to demonstrate that their properties do, in fact, contribute to decoding performance. The perturbations that should be applied may depend on what authors would like to claim regarding their decoder. If it is claimed that the fine-grained pattern is important, spatial smoothing could specifically test the spatial frequency or scale at which decoding can be completed. Alternatively, if the decoder is said to be sparse and that its constituent elements are necessary for decoding, then random sampling of the weights would specifically test the necessity of its weights.

2. Comparisons of the decoders to a negative control rather than just “chance”. To claim that the algorithmic process used to tune the weights of a given decoder improves performance, one should test the performance of the decoder at each stage of its creation. For example, pPV started with brain activity maps, then used contrasts and conjunction analysis, and then applied SVM; however, brain activity maps alone have similar decoding performance as the final pPV model (Fig 6). The gain of more sophisticated modeling approaches over more parsimonious ones should be evidenced rather than assumed.

3. Discrimination and identification performance should not be conflated. Many decoding and prediction studies rely on AUC—a measure of discrimination. However, in practical situations, identification is arguably of greater interest. Here, we used distributional overlap as an agnostic approach to quantifying identification, but this is inadequate for practical purposes. Rather, investigators should rely on decision theory to pick cutoffs that have appropriate error rates—or expected costs and benefits—for their application or utility function. Ideally, such cutoffs should not change from task-to-task or sample-to-sample, as decoding performance in new samples and environments is of the utmost importance. If probabilistically identifying, authors should demonstrate that their model is properly calibrated.

4. Use realistic or ecologically valid tests to demonstrate decoding performance. The metrics used to assess decoding performance should reflect the problem one is trying to solve with the decoder. For example, mixing within- and across-subject performance can mislead readers if the ultimate goal is one of the two. Furthermore, if one wishes to apply decoders to real-world or clinical settings in which no known stimuli is being applied, many stimulus-derived decoders may not generalize well. That is, although a decoder may perform well with stimuli, it will not necessarily generalize to clinical settings if that is the ultimate goal. Researchers should test the decoder in the setting or on the level about which they would like to make inferences.

5. Share their data and decoder. Open science practices enable others to scrutinize, apply, and build upon the original work. Indeed, the analyses we presented in this paper would not have been possible without authors’ willingness to make their work available.

6. Establish boundary conditions. It is not only important to know when decoders perform well, but also when they perform poorly. This may involve introducing more control stimuli, more difficult decoding tasks (e.g., identification instead of discrimination), or applying to more general samples or populations (e.g., chronic instead of acute pain, see for example (Lee et al., 2021)).

By implementing the above recommendations, we believe researchers and readers can better understand the properties and limitations of decoders, in turn making gaps in the literature more transparent and eluding optimistic biases. Thus, these recommendations will enable authors to easily demonstrate the novelty of their decoders. Similarly, it may be prudent for neuroimaging researchers to develop and implement reporting guidelines for decoding studies, much like Transparent reporting of a multivariable prediction model for individual prognosis or diagnosis (TRIPOD) in the clinical prediction literature.(Collins, Reitsma, Altman, & Moons, 2015)

6. Conclusion

Mental state decoding is a large, impactful subfield of cognitive neuroscience. Many approaches to decoding have been proposed and implemented. Here, we systematically assessed just one such implementation of multivariable decoders, which uses fixed voxel weights. Our findings reveal misconceptions that are widespread in the brain imaging community and amplified by some oversold decoding studies. On the other hand, our findings also agree with much of the literature regarding the spatial resolution of decoding. In turn, this work extends our understanding of mental state decoders, provides insight into decodability constraints, and forms the basis for several practical takeaways that researchers can readily implement in their own work. Importantly, the limited and inadequate performance of fixed-weight across-subject decoders, especially regarding identification, pose strict bounds on their utility in the domains of medical and legal decision-making.

Data and code availability

Data used in this paper is available on: ftp://openpain.org/LimitsDecoding

Code used in this paper is available at: https://github.com/avigotsky/hardlimitshttps://github.com/avigotsky/hardlimits

Raw data for Dataset 6 is available at: https://openneuro.org/datasets/ds000158/versions/1.0.0https://openneuro.org/datasets/ds000158/versions/1.0.0