Figure 3.

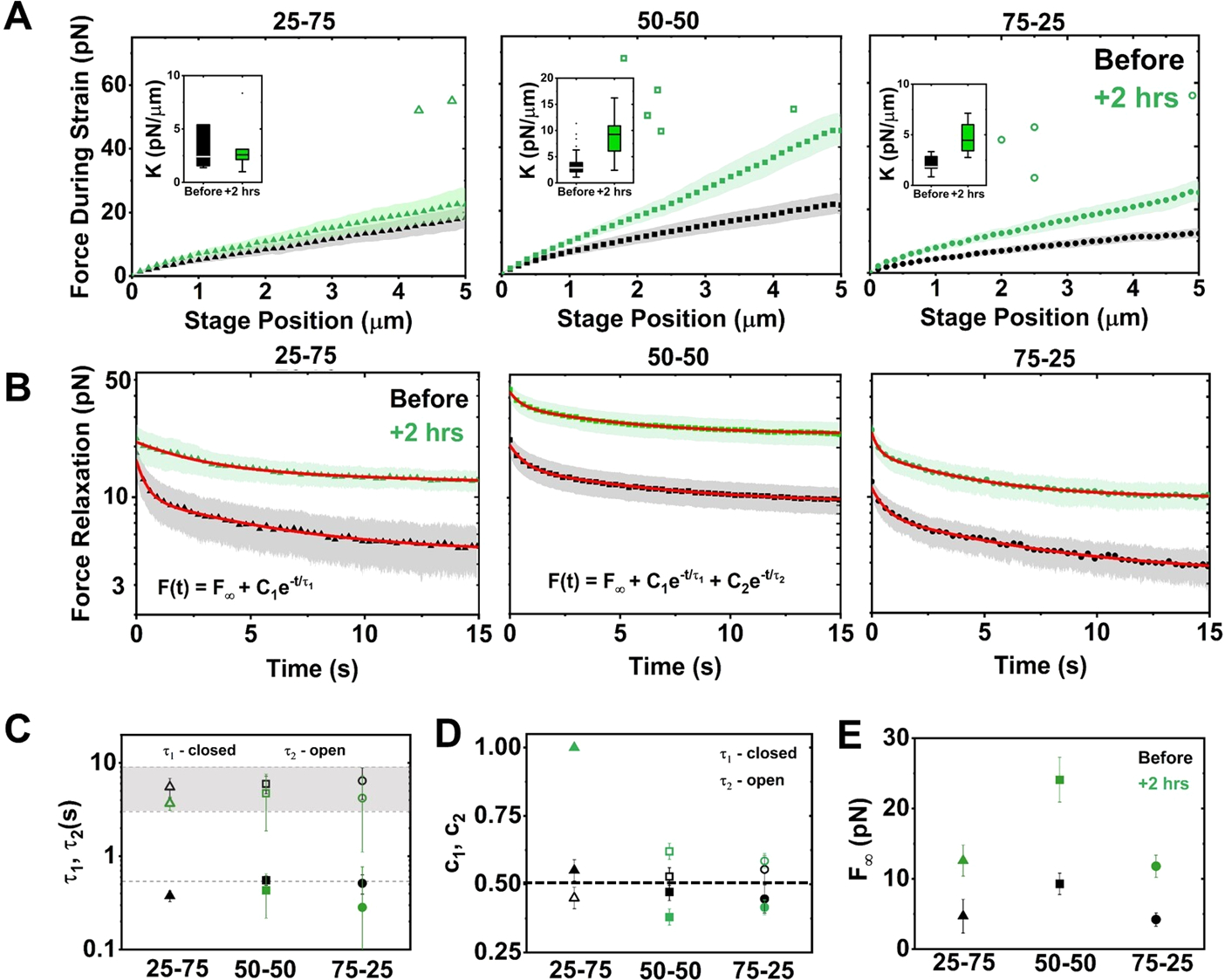
Myosin-driven restructuring increases the nonlinear force response and suppresses relaxation of actin–microtubule composites. (A) Average force F(x) exerted on the bead during nonlinear strain, measured before (black) and 2 h after (green) myosin activation, for composites with actin–tubulin percentages of 25–75 (left), 50–50 (middle), and 75–25 (right). Shaded regions along each curve indicate standard error. Insets: boxplots of differential modulus, K = dF/dx, found as the slope of F(x) for each trial. (B) Relaxation of force versus time following strain, measured before and 2 h after motor activation. Nearly all curves are well fit to a sum of two exponentials and a nonzero offset: F(t) = F_∞ + C₁e^−t/τ₁ + C₂e^−t/τ₂. The 25–75 relaxation after activation fits to a single exponential. Fits are shown as red lines. (C) Time constants corresponding to fast (τ₁, closed symbols) and slow (τ₂, open symbols) modes determined from fits in (B) for relaxations measured before (black) and 2 h after (green) activation. The dashed line corresponds to predicted actin bending time scale τ_B, and the gray region corresponds to previously measured reptation times for steady-state composites. (D) Relative contributions of the fast (c₁) and slow (c₂) modes determined from the fits in (B). Dashed horizontal line indicates equal contribution from both modes. (E) F_∞ determined from the fits shown in (B), corresponding to the force that is sustained at the end of the relaxation period.