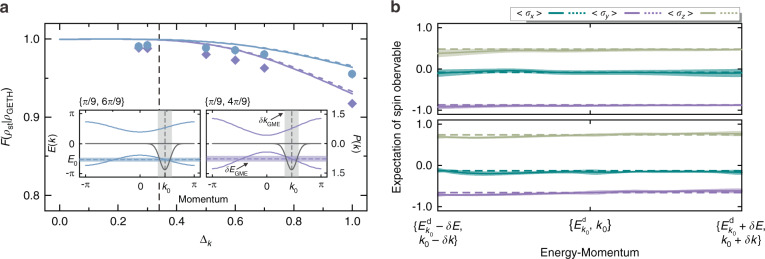
Fig. 4 . Verifying the generalized eigenstate thermalization hypothesis.

a Fidelity $\mathcal{F}\left({\rho }_{\mathrm{st}}\mid {\rho }_{\mathrm{GETH}}\right)$ between the measured steady state ${\rho }_{\mathrm{st}}$ and GME prediction ${\rho }_{\mathrm{GETH}}$ against the standard deviation Δ_k for a walk with (blue circles) ${\mathcal{H}}_{\mathrm{eff}}\left(\pi /9,6\pi /9\right)$ and (purple diamonds) ${\mathcal{H}}_{\mathrm{eff}}\left(\pi /9,4\pi /9\right)$. The colored dashed and solid lines represent the theoretical simulations for the steady state estimated by ${\overline{\rho }}_{t=10}$ and ${\overline{\rho }}_{t\to \infty }$, respectively. The dashed black line represents the upper bound of the initial Δ_k; below this line, the fidelity always approaches 1. The insets illustrate the effective band structures (colored solid lines with left-hand scale) and occupations of the initial state (with ${\mathrm{\Delta }}_k=0.3$ as an example) on the two bands (gray curves with right-hand scale). The expectation of the energy and momentum of the initial state is E₀ and k₀, respectively. In the insets, the vertical gray regions and horizontal colored regions show the chosen momentum window with $\delta k=0.4$ and associated energy window. b Measured expectations of the three spin observables of the reconstructed spinor eigenvectors ${\mathbf{n}}_{\mathcal{H}}\left(k\right)$ within the chosen energy-momentum window. The upper and lower panels show the results for ${\mathcal{H}}_{\mathrm{eff}}\left(\pi /9,6\pi /9\right)$ and ${\mathcal{H}}_{\mathrm{eff}}\left(\pi /9,4\pi /9\right)$, respectively. The colored dashed lines give the theoretical results for ${\rho }_{\mathrm{GETH}}\left(E_{k_0}^{\mathrm{d}},k_0\right)$, and the translucent shadings illustrate the statistical errors