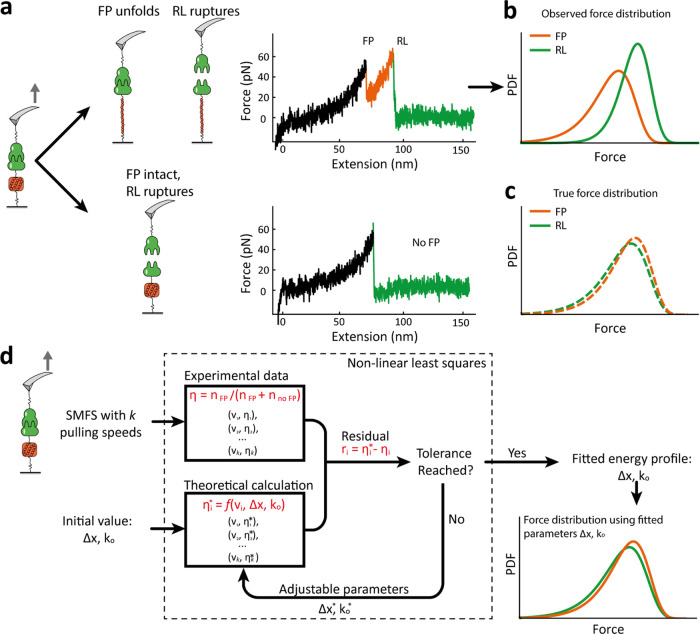
Figure 2.

Biasing effect and correction algorithm based on η residuals. (a) Two pathways are possible in an atomic force microscope (AFM)-SMFS assay using an RL complex to unfold an FP domain. Typical experimental data (middle) showing FP unfolding followed by complex rupture (upper trace) or complex rupture prior to FP unfolding (lower trace). (b) Biased force distributions of RL rupture (green) and FP unfolding (orange) obtained from analysis of force extension exhibiting FP unfolding. (c) True force distribution (unbiased) of the RL rupture events can be obtained by analyzing traces from both pathways. To obtain the true distribution of FP unfolding forces, a correction algorithm is required. (d) Overview of the correction algorithm to extract the true distribution of FP unfolding forces from biased experimental AFM-SMFS observations using a nonlinear least-squares fitting of η. Initial guesses for energy landscape parameters (in this case, Bell–Evans k₀ and Δx) for the FP are obtained by direct fitting of the biased experimental FP unfolding force distribution. Based on the guess, the theoretical eta value (η*) is numerically computed using eqs 4 and 5 and compared with the experimentally observed η. This process is repeated with updated energy landscape parameters for the FP domain until the tolerance on η residuals is reached.