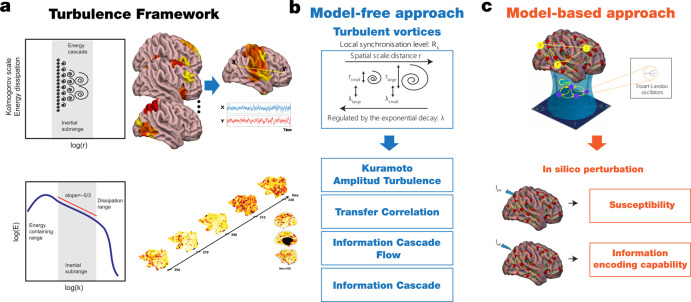
Fig. 1. Overview of framework.

a Turbulence in fluids is one the most common dynamical regime where the mixing motion governs (left panel). The energy cascade, i.e., how the energy travels across scale while dissipated and the statistical properties defined as power laws on the energy levels and structure functions (bottom panel) determine the turbulent behaviour of the fluid. The analogy between brain activity and Turbulence has been recently demonstrated using resting state data from a large dataset of 1,003 healthy human participants. b Model-free approach. The turbulent behaviour of brain activity is reflected in the similarity between the local level of synchronisation, determined by the local Kuramoto order parameter (R) at different scales (λ), and vortex with different spatial scales in fluid dynamics. The spatial scale (r) of the vortex is inversely related with the exponential decay of the local Kuramoto order parameter (λ). The turbulence regime also endows the brain with an efficient information cascade measured as the correlation of the local level of synchronisation across scales (Information Cascade Flow). The average across scales of the information cascade flow is defined as the Information cascade. The Transfer Correlation quantified as the correlation of local synchronisation across space at different scales also characterises the brain’s information processing. c In the Hopf whole-brain model, the dynamics of each brain area are described through a Stuart Landau non-linear oscillator. The system of local oscillators is connected through the anatomical connectivity to simulate the global dynamics, capable of reproducing statistical observables from fMRI data. We used as structural connectivity the long-range connections (LR) from human diffusion MRI measurements on top of an exponential distance rule (EDR) to fit the empirical functional connectivity as a function of the Euclidean distance (following the relation between the Kolmogorov’s second-order structure-function and the traditional FC). Using whole-brain modelling allows obtaining measures that rise from the in silico perturbative approach. We simulated external stimuli and evaluated the model’s reaction for each brain state by quantifying the susceptibility and information capability measures.