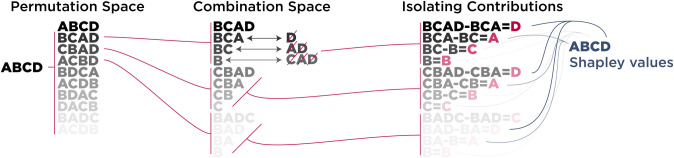
Fig 3. Visual depiction of the MSA algorithm.
Since there are 2N possible combinations of coalitions, an analytical solution for the Shapley value of elements in large systems is computationally prohibitive. Therefore, we sampled 1,000 permutations from all N! possible orderings (permutation space) and used them to dictate which coalitions to perturb (combination space). The contribution of elements to each coalition was then quantified by calculating the difference between the score of the coalition with the element (e.g., {B, C, A}) and the score of the same coalition without the targeted element (i.e., {B, C} to isolate A). Shapley value of each element was then calculated by averaging individual contributions of each element to the formed coalitions.