Graphical abstract
Keywords: Coalescence, Ultrasound, Emulsion, Numerical Modeling, Transducer
Highlights
-
•
Numerical assessment of the coalescence of two water droplets in oil was conducted.
-
•
The transducer materials assessed are PZT, LiNbO3, ZnO, AlN, PVDF, and BaTiO3.
-
•
Interfacial tension, droplet diameter and US voltage showed the most notable effect.
-
•
Variation in the pressure distribution with US frequency and material was observed.
-
•
Possible attenuation of the US waves and various inhibitive effects were discussed.
Abstract
In this study, a numerical assessment of the coalescence of binary water droplets in water-in-oil emulsion was conducted. The investigation addressed the effect of various parameters on the acoustic pressure and coalescence time of water droplets in oil phase. These include transducer material, initial droplet diameter (0.05–0.2 in), interfacial tension (0.012–0.082 N/m), dynamic viscosity (10.6–530 mPas), temperature (20–100 °C), US (ultra sound) frequency (26.04–43.53 kHz) and transducer power (2.5–40 W). The materials assessed are lead zirconate titanate (PZT), lithium niobate (LiNbO3), zinc oxide (ZnO), aluminum nitride (AlN), polyvinylidene fluoride (PVDF), and barium titanate (BaTiO3). The numerical simulation of the binary droplet coalescence showed good agreement with experimental data in the literature. The US implementation at a fixed frequency produced enhanced coalescence (t = 5.9–8.5 ms) as compared to gravitational settling (t = 9.8 ms). At different ultrasound (US) frequencies and transducer materials, variation in the acoustic pressure distribution was observed. Possible attenuation of the US waves, and the subsequent inhibitive coalescence effect under various US frequencies and viscosities, were discussed. Moreover, the results showed that the coalescence time reduced across the range of interfacial tensions which was considered. This reduction can be attributed to the fact that lower interfacial tension produces emulsions which are relatively more stable. Hence, at lower interface tension between the water and crude oil, there was more resistance to the coalescence of the water droplets due to their improved emulsion stability. The increment of the Weber number at higher droplet sizes leads to a delay in the recovery of the droplet to spherical forms after their starting deformation. These findings provide significant insights that could aid further developments in demulsification of crude oil emulsions under varying US and emulsion properties.
1. Introduction
The de-emulsification and separation of stable water-in-crude oil emulsions continue to gain significant attention. This is due to the unavoidability of the formation of emulsions during crude oil production, refining and transportation, and the subsequent detrimental economic and environmental impacts of their continued presence. Emulsions, which majorly occur in the form of water-in-oil [1], [2], [3], is usually found during oil production processes due to the presence of underground formation water which could attain 90–95% [4], [5]. The challenge becomes intensified when extended duration of reservoir usage, and continued utilization of water for flooding and drilling are present. Without proper treatment of the produced emulsions, tremendous negative impact could be caused. For instance, increased viscosity of emulsions leads to prohibitive costs of pumping [6]. In addition, emulsions could result in catalyst poisoning during refining and pipeline corrosion in the course of transportation [6], [7], [8], [9], [10], [11], [12]. Consequently, different methods of dehydration of water-in-oil emulsions have been studied. These include physical [13], [14], [15], [16], chemical [3], [17] and biological [18], [19], [20] approaches. Physical dewatering processes like electrostatic [13], thermal [14], membranes [15] and ultrasound [16] constitute an important portfolio in the coalescence operation. This is because the physical route could overcome the challenges of extended time requirement for separation with biological methods which could hamper oil production processes. But equally important is the, attenuation of the negative environmental drawbacks that exist with chemical approaches.
The utilization of ultrasound in the demulsification of water-in-oil and oil-in-water emulsions, in contrast to other physical approaches, offers a viable alternative because of their low cost, simplicity, and significant efficiencies. Hence, the assessment and optimization of US assisted coalescence and demulsification have been conducted in numerous studies [11], [21], [22], [23], [24]. Significant efficiency upgrade with US inclusion have been reported of varying degrees such as 65% by Antes et al. [11], ∼70% by Luo et al. [22], ∼85% by Sadatshojaie et al. [23] and more than 93% by Wang et al. [21] and Khajehesamedini et al. [24]. However, the vast majority of these studies were experimental with relatively few reports on numerical simulation. Although empirical studies are certainly important to the coalescence process, further developments require numerical and fundamental investigations. Numerical studies provide the advantage of relatively fast and low cost comprehensive studies of the parameters variation which might be expensive and difficult to achieve using experiments.
In one of such studies, Xu [25] examined the numerical model of the coalescence of two air bubbles in water. Different parameters such as inclusion of ultrasound, bubble radius without ultrasound, US frequency and pressure were evaluated. They showed that the usage of US improved the coalescence time for bubbles of radius 0.1 mm. Whilst the coalescence time without US was 0.14 ms, the coalescence of the bubbles in the presence of US was completed in 0.09 ms. Furthermore, they reported that at elevated acoustic pressure with amplitudes nearing 1 MPa, the bubbles were compressed and aggregated at the antinode. Although the findings are significant, the study was limited to the evaluation of air bubbles in water, and lacks further evaluation of important parameters such as interfacial tension, viscosity etc. In addition, the effect of different transducer materials was not assessed. This is crucial to the implementation of more environmental friendly alternative to the lead based PZT transducers which are widespread. In another study, Nasiri et al. [9] investigated the ultrasound supported removal of oil from oil-in-water emulsion using artificial neural network. Although they reported good agreement with experimental data, the model did not consider the impact of confinement as represented by the compartment radial and axial dimensions. The study focused on experimental validation, but a rigorous assessment of the influence of different parameters is missing. The US frequency was set at 20 kHz and 5% sunflower oil in water was assessed. Mohsin and Meribout [26] studied the numerical simulation of the coalescence of water droplets in water-in-oil emulsion with the application of US. The study showed that there was similarity in the pressure field at 5, 10 and 15% water content. However, the study was limited to a single frequency and limited assessment of the coalescence dynamics and influencing parameters were considered. Khajehesamedini et al. [24] developed a simplified model based on the population balance approach for the observation of the US assisted coalescence of water droplets in oil continuous phase. The assessment included three different crude oils (Cheshmeh Khosh, Gachsaran 1 and Gachsaran 2). Major drawbacks of the simplified model are that the radial and axial gradients of fluid volume fraction across the dimensions of the compartment were neglected and only a single US frequency of 20 kHz was used.
Several studies related to the coalescence of oil droplets in water continuous phase have been reported by Pangu and Feke [62], [63], [64]. In one of such experiment, Pangu and Feke [64] designed and examined the effectiveness of ultrasound in the separation of emulsion consisting of oil droplets from water continuous phase in a rectangular compartment. The chamber consists of a PZT transducer and stainless steel reflector at opposite sides, with a distance of 1.22 cm between them. Effect of various parameters including porous media type, pore size, electrical power and residence time were assessed. The residence time showed significant influence on the demulsification. The oil collection performance increased from 27 % at 34.7 s to 75 % at 69.4 s. The demulsification behavior with different transducer electrical power indicated that at 25.8 W and 6.3 W, the oil collection efficiencies were 75% and 62%, respectively. Further increment in the electrical power to 47.2 W resulted in a slower gain in the separation performance (80%). Although the porous media type exhibited a considerable effect on the oil collection performance, the pore size provided little differences in the demulsification. Polymer mesh provided the highest separation performance with values around 75% and 80% as compared to glass beads with oil collection of about 31 % and 52 % at 25.8 W and 47.2 W, respectively. Lowering the pore mesh size from 10 to 30 pore per inch resulted in an improvement of 5% in the oil collection. In a different study, Pangu and Feke [63] assessed the influence of ultrasonic waves on the relative movement of binary droplets of oil in water continuous phase. The study consists of a mathematical model which was validated with experimental data. The mathematical model consists of 1D acoustic field and spherical oil droplets in non-miscible water phase in the absence of surfactants and bulk flow. The assumptions made includes the Newtonian behavior for oil and water, irreversible coalescence, negligible inertial force and insignificant Brownian diffusion due to high Peclet number. The driving forces includes body forces (primary acoustic force, gravity and buoyancy force) and inter-droplet forces (hydrodynamic interaction, secondary acoustic forces and van der Waals forces). Based on these forces, the Batchelor equation was utilized to determine the relative trajectory of the oil droplets [65].
| (1) |
where is the relative hydrodynamic mobility, is the relative velocity contribution from body forces, and are the unit vectors along the tangential and radial directions, is the van der Waals potential, M is the asymmetric relative mobility function, L and G are the axisymmetry relative mobility function, is the relative angle to the vertical axis, is the relative droplet velocity, is the secondary acoustic force, r is the distance between the droplets’ centers.
The experimental investigation consists of chamber with similar description in Pangu and Feke [62]. Vegetable oil droplets of sizes between 24 and 193 µm forms 0.01 vol% in aqueous medium. The transducer has frequencies of ∼0.5 and 2 MHz and an estimated energy density of 90 J/m3. The relative motion of the binary droplets was used to obtain the volume cleared due to coalescence. Sensitivity analysis based on emulsion properties and acoustic parameters were conducted. The predicted droplets relative trajectory and coalescence time showed good agreement with experimental findings. However, the prediction of the coalescence kinetics deteriorates as the binary droplets get closer to each other. In another study, Pangu and Feke [62] developed a model to observe the coalescence of vegetable oil droplets in water under the influence of ultrasonic waves. The model is developed based on the population balance and it was utilized to estimate the transformation of the variations of the sizes of the droplets as well as the determination of the overall rate of coalescence. The emulsion consists of 8 µm oil droplets of 0.5 vol% in water. The ultrasound was operated at frequencies of 0.525 and 1.69 MHz and the estimated energy densities used was between 0.25 and 20 J/m3. The experimental set-up described in their earlier study [64] was utilized for the validation of the model. The validation results indicated that there was good agreement between the developed model and the experiments. However, there was a general under-prediction of the experimental data. This difference was linked to the gradients in the energy density in the demulsification compartment. Although the findings by Pangu and Feke [62], [63], [64] have provided important findings, the studies were focused on the demulsification of vegetable oil in water emulsion. In addition, the effect of different piezoelectric materials, and emulsion properties such as interfacial tension, viscosity and temperature were not investigated.
Based on the assessment of the reported studies on the modeling of the US coalescence of droplets in oil continuous phase, it becomes evident that more work is required to improve our knowledge and operation of such a process. Hence, the development of an enhanced numerical model that considers the axial and radial dimension effects, as well as the detailed optimization of the coalescence process is needed. In this study, the numerical assessment of the effect of various parameters on the acoustic pressure and coalescence time of water droplets in oil phase was conducted. These include the ultrasound parameters such as the transducer material, US resonance frequency and the US power. Moreover, emulsion properties such as initial droplet diameter, interfacial tension, dynamic viscosity and temperature were considered. The evaluation of these variables is important in assessing relevant lead free transducer materials, and a wide range of crude oil and process conditions which are found either in oil fields or laboratory setups. Furthermore, the study would aid in the development and optimization of ultrasound assisted dewatering process. Demulsification of emulsions in pipelines allows for the assessment of the performance of US for inline dewatering during transportation, thus avoiding bulky and costly storage tanks.
2. Methodology
2.1. Model description and boundary conditions
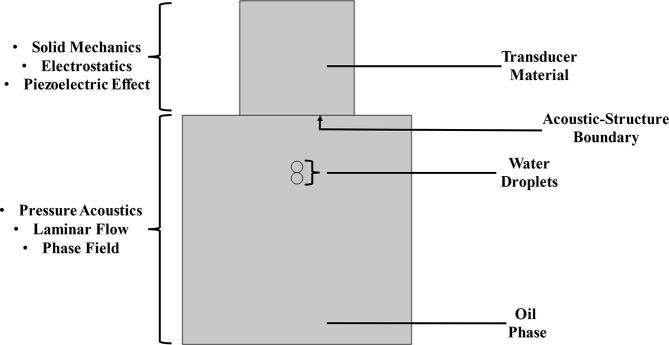
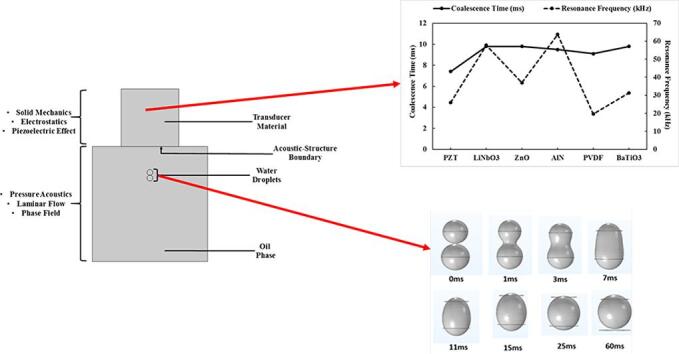
The evaluation of the coalescence of binary water droplets in crude oil phase under various acoustic parameters and fluid properties was conducted with COMSOL Multiphysics 5.6. The numerical model consists of ultrasound transducer and fluid flow equations (Fig. 1). The US transducer section actuates the acoustic pressure which would drive the droplet coalescence in the fluid flow section. The US transducer consists of a piezoelectric material of 25.4 mm diameter and 25.4 mm height which operate based on the principles of piezoelectricity to convert electric potential to mechanical strain. Piezoelectricity was activated through the solid mechanics and electrostatics modules as well as the piezoelectric effect multiphysics. The fluid flow section occurs in a 50.8 mm diameter pipe which contains two water droplets in oil phase. Water droplets of diameters between 1.27 and 6.35 × 10−3 m were assessed. Moreover, crude oils of different properties were studied for their effect on the acoustic pressure and coalescence time (Table 1). The coalescence was simulated using the pressure acoustics, laminar flow and phase field modules as well as two phase flow multiphysics. The transducer and fluid flow sections were linked through the acoustic-structure boundary.
Fig. 1.
Description of the components of the piezoelectric transducer and pipe coalescence model.
Table 1.
Properties of the crude oil utilized for the model predictions.
| Crude Oil Properties | |
|---|---|
| Density (g/cm3) | 0.85 |
| Viscosity (mPas) | 10.6–530 |
| Interfacial tension (mN/m) | 0.062–0.82 |
| Speed of sound (m/s) | 1480 |
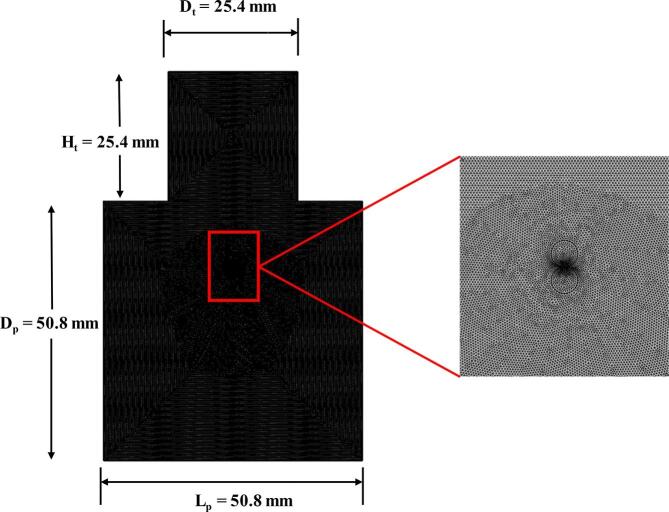
The mesh utilized for the model development has 102,152 triangular elements with mesh quality of 0.96 (Fig. 2).
Fig. 2.
Mesh utilized for the droplet coalescence model.
Where Dp is the pipe diameter, Dt is the transducer diameter, Ht is the height of transducer, and Lp is the pipe section length.
2.2. Governing equations
They consist of the constitutive stress-charge form, Gauss and electric potential equations for the description of the transducer [27]:
| (2) |
| (3) |
| (4) |
| (5) |
where is the electric displacement field, e is coupling properties, is the strain, is the permittivity of free space, is the relative permittivity, is the electric potential, is the stress, is the material stiffness, is the transpose of the coupling properties, is the volume charge density and V is the applied voltage.
The pressure acoustic in the pipe verifies the Helmholtz equation [27]:
| (6) |
where
| (7) |
| (8) |
where ρ is the piezoelectric domain density; pt is the total pressure; pb is the background pressure; qd is the monopole domain source; keq is the wave number consisting of the ordinary wave number k, the azimuthal wave number and the out of plane wave number kz; Qm is the monopole domain source; and c is the speed of sound.
Furthermore, the coalescence model includes the continuity equation and the incompressible form of the Navier-Stokes equations [27]:
| (9) |
| (10) |
where u is the fluid velocity vector, t is the time, ρ is the density, µ is the viscosity, is the interfacial tension, p is the pressure, is the US acoustic force, g is gravity.
Based on the phase field, the interfacial force is represented as [27], [28]:
| (11) |
where G is chemical potential and is a phase field dimensionless function.
The chemical potential was determined by [27], [28]:
| (12) |
where is the mixing energy density and is the level thickness.
The volume fraction, viscosity and density is described as [27]:
| (13) |
| (14) |
| (15) |
Where is the volume fraction, is the water density, is the crude oil density, is the water viscosity and is the crude oil viscosity.
The phase field is defined based on the following [27]:
| (16) |
| (17) |
where is the surface tension, is the external force which is mainly the US acoustic force, is the phase field support variable.
The mixing energy density is obtained based on the following equation which relates it to the surface tension () and the parameter controlling the interface thickness () [27]:
| (18) |
The numerical procedure commenced with the solution of the electrostatics and solid mechanics physics in the transducer to simulate the reverse piezoelectric effect. The charge conservation Eq. (3) provides the electric displacement field which is required to obtain the material strain through the constitutive Eqs. (1), (2). Subsequently, the ultrasound force was determined with the pressure acoustic model and was included in the fluid flow field as a volume force. The Navier Stokes equation (9) was solved for both the oil and water phases, and the phase field model was used to determine the coalescence and movement of the water droplets. The two phase-phase field multi-physics was utilized to couple the interaction between laminar flow field and the phase field droplet movement. The boundary conditions imposed on the model includes roller conditions and ground potential at the top and bottom of the transducer. In addition, ultrasound power of 0–40 W was applied to the transducer. The no slip boundary condition was used at the pipe walls. The initial conditions of the displacement and velocity fields are zero, and the pressure in the fluid region was set as that of the atmospheric condition.
3. Results and discussion
3.1. Model validation
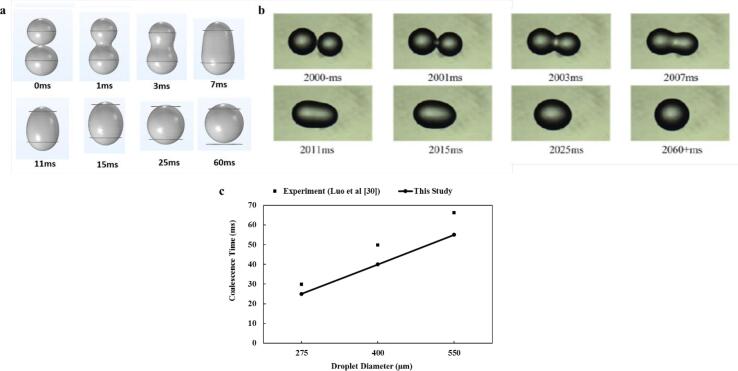
The coalescence model was validated with the work of Luo et al. [29] using three different water droplet diameters of 275, 400 and 550 µm. White oil of density of 878 kg/m3 and dynamic viscosity of 1410 mPas was used. While the density, dynamic viscosity and speed of sound of water were 998.2 kg/m3, 1 mPas and 1482 m/s, respectively. The USW has a frequency of 20 kHz and a high speed camera was utilized to capture the coalescence. The results of the present simulation are in reasonable agreement with the experimental values reported by Luo et al. [29]. Generally, the trend and magnitude of the coalescence time was well captured at the three droplet diameters (Fig. 3). The coalescence time increases at higher initial droplet size because larger droplets require more time for the stabilization of their deformation curves. Therefore, the numerical model was utilized for further investigation of the parametric analysis of the coalescence process.
Fig. 3.
Model validation based on the transformation of the water droplets in the oil phase a This study b Experimental data of Luo et al [29] c Quantitative validation of the developed coalescence model at different droplet diameters.
The discrepancy between the model prediction and the experimental data could be associated with the experimental error and the spatial non-uniformity of the ultrasound energy density in the experiments. The energy density gradients in the compartment produces lateral ultrasound forces. Consequently, the lateral forces populate the droplets in areas of local energy density maxima which gives rise to differences in the experimental data as compared to the model results. This description has been mentioned as well in the work of Pangu and Feke [62]. In their study on ultrasound demulsification, the presence of spatial non uniformity of the ultrasound energy density and their impact of coalescence has been reported. They observed mismatch in the experimental values of the evolution of the average radius of the emulsion droplets as compared to the model predictions. The experiments were consistently underpredicted by the model estimation and this was attributed to the energy density gradients in the experiments. Likewise, discrepancy between the experiments and model estimations of the coalescence time of binary oil droplets in water continuous phase was observed in another study by Pangu and Feke [63]. The discrepancy is significant and approaches more than 20% in some cases. Besides the energy density gradients, there are experimental errors that have been reported by numerous groups on the ultrasound assisted coalescence and demulsification of oil-in-water and water-in-oil emulsions. Errors in experimental investigation of ultrasound coalescence have been reported in the studies of Ronchi et al. [66], Antes et al. [11], Antes et al. [67], Atehortua et al. [38], Luo et al. [22]. These errors could make it challenging to obtain enhanced model prediction compared to experimental reports.
3.2. Mesh sensitivity study
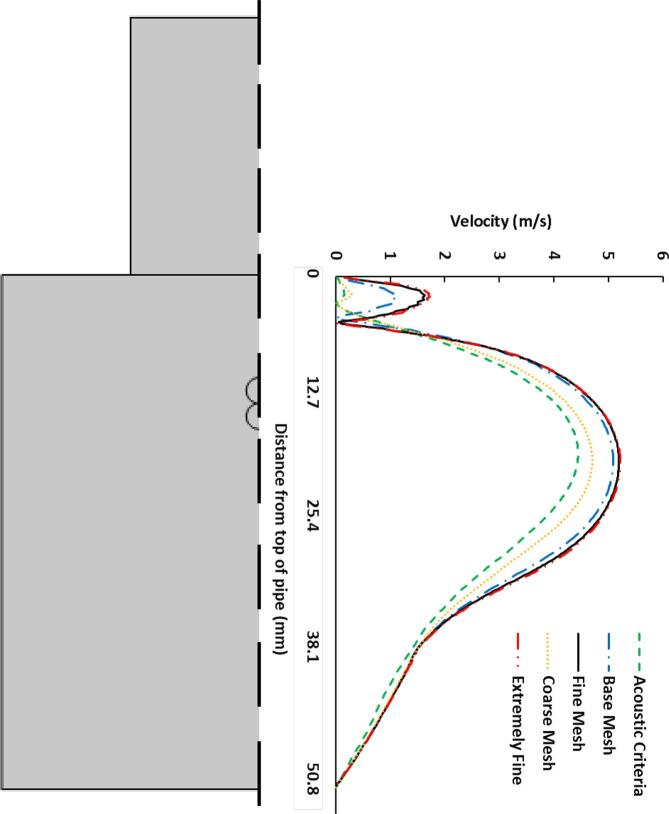
The mesh sensitivity study was conducted in order to ensure that the solution is independent of the grid. Five different meshes were used (Table 2). The acoustic criteria was selected as with second order element. This criterion is essential for accurate prediction of the ultrasound propagation [54], [55], [56], [57], [58]. Although the acoustic criteria provide reasonable estimation for the ultrasound, the predictions for the laminar flow was inadequate. Hence, the coarse, base, fine and extremely fine meshes were selected as more refined grids relative to the acoustic criteria mesh. Although the acoustic criteria mesh predicted the US pressure reasonably, it was deficient in the estimation of the flow performance. Similarly, the coarse mesh was inadequate in the determination of the flow velocity along the radial centerline of the pipe. The flow prediction improved significantly for the base, fine and extremely fine meshes. Since the base mesh showed a slight difference relative to the extremely fine mesh, the mid-sized fine mesh was utilized for further studies as it provides an improved accuracy and requires less computational time (Fig. 4).
Table 2.
Types of meshes.
| Mesh Type | Number of mesh elements |
|---|---|
| Acoustic criteria | 4493 |
| Coarse | 8314 |
| Base | 37,409 |
| Fine | 101,434 |
| Extremely Fine | 230,205 |
Fig. 4.
Mesh sensitivity based on the fluid velocity along the pipe radial direction.
3.3. Temporal sensitivity study
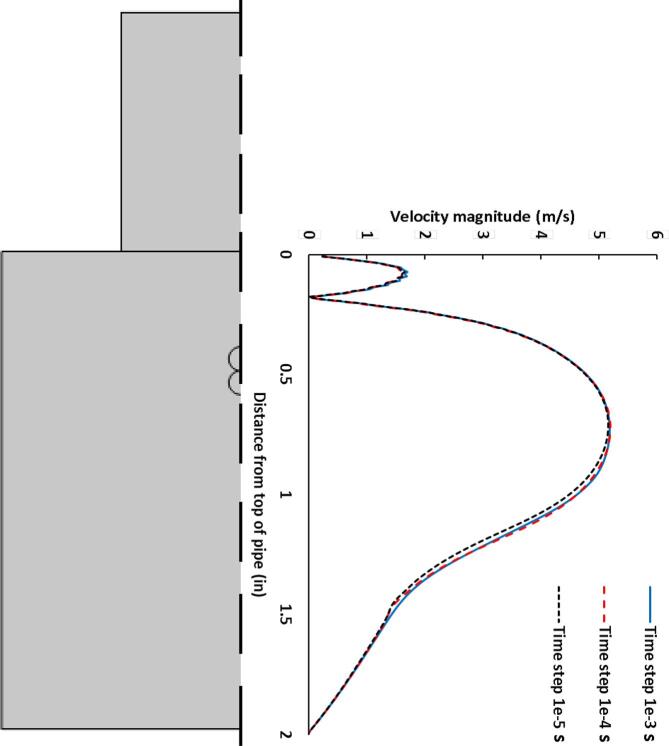
The time step sensitivity of the analysis is crucial in order to avoid output values that varies temporally. Hence, three different time steps of 10 µs, 100 µs and 1 ms were assessed. There were minimal differences between the three time steps at distances between 0–17.78 mm (0–0.7 in) and 40.64–50.80 mm (1.6–2 in) from the top of the pipe. However, there were slight differences between 17.78 and 40.64 mm (0.7–1.6 in) from the top of the pipe. Consequently, the time step of 100 µs was utilized in order to obtain reasonable results whilst lowering the computational time required for solution convergence (Fig. 5).
Fig. 5.
Time sensitivity based on the fluid velocity along the pipe radial direction.
3.4. Parametric study
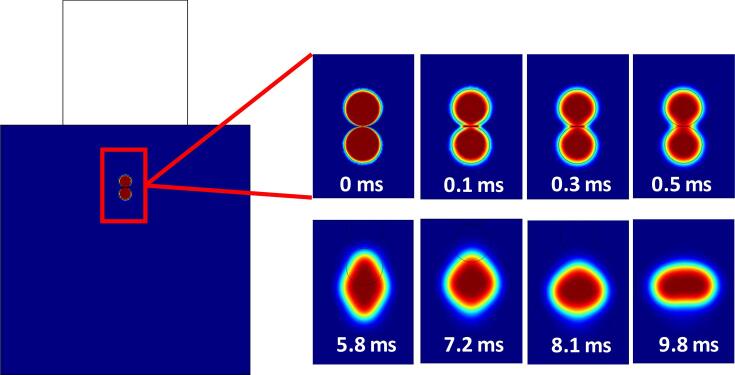
The droplets’ motion and coalescence are generally influenced by body forces (primary acoustic forces and net gravitational-buoyancy force) and inter-droplet forces (secondary acoustic forces, van der Waals forces and hydrodynamic association). The van der Waals forces were neglected as they have little impact on the coalescence. The coalescence of the droplet begins with the weakening/thinning of the liquid film between the water droplets. The weakening of the film could be observed at 0.1 ms with the formation of a disc between the droplets. Thereafter, the film undergoes significant breakage along the droplet sides starting at 0.3 ms. After the rupture of the film, the droplets then undergo deformation in the axial direction. The deformation proceeded until a larger coalesced droplet was formed at 8.1 ms (Fig. 6) [30], [31], [32], [33]. Similar observations of the coalescence of droplets were highlighted by Yamashita et al, 2017 [34] and Pons, 2000 [35]. The coalesced droplet then begins to compress under continued application of USW at 9.8 ms. The compressing phenomenon has been reported as well in the study of Xu [25] for air bubbles in water under increased US pressure.
Fig. 6.
Description of droplet coalescence process with time.
3.4.1. Transducer material type
The effect of six different piezoelectric material types (BaTiO3, PZT, AlN, PVDF, ZnO and LiNbO3) on the coalescence of two droplets of water in oil continuous phase was examined. The US transducer materials were excited at their natural frequencies in order to ensure that optimal waves are produced. The acoustic pressure distribution was then determined based on the resonance frequencies of each piezoelectric material. The result showed that the US transducer material has considerable influence on the propagation mode and magnitude of the acoustic waves. The difference in the pattern of propagation of the US in the fluid media can be associated with the crystal orientation (Table 3). This vast variation in their structures can be associated with the different acoustic distributions observed. In their study, Kuroiwa et al. [36] highlighted that the large amount of the piezoelectric properties is attributed to their crystal orientation.
Table 3.
Crystal structures of the different transducer materials.
| Piezoelectric material | Crystal orientation |
|---|---|
| PZT | Perovskite |
| PVDF | Orthorhombic |
| LiNbO3 | Trigonal |
| ZnO | Wurtzite |
| AlN | Hexagonal |
| BaTiO3 | Tetragonal |
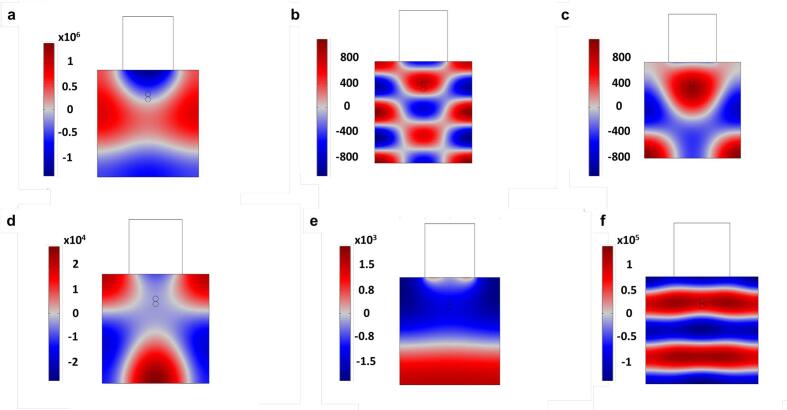
As regards the magnitude of the US pressure, the increasing trend of the total acoustic pressure followed the order: PZT > LiNbO3 > BaTiO3 > PVDF > AlN > ZnO under natural frequency excitation (Fig. 7). The differences in the maximum US pressure for the various materials could be associated with the varying acoustic impedance and piezoelectric coefficient. Although the PVDF has the least acoustic impedance (2.7 × 106 kg/m2s), the acoustic pressure was lower than that of PZT. For example, whilst PVDF showed a maximum pressure of 5 × 102 Pa, PZT has a peak pressure of 3.5 × 105 Pa. The possible reason for this is due to the high piezoelectric coefficient of 600 pC/N of PZT as compared to 33 pC/N in the case of PVDF. The piezoelectric coefficient of Lithium niobate could reach 70 pC/N which makes them have an intermediate pressure between PZT and PVDF.
Fig. 7.
Acoustic pressure for different piezoelectric materials a. PZT b. AlN c. ZnO d. BaTiO3 e. PVDF f. LiNbO3.
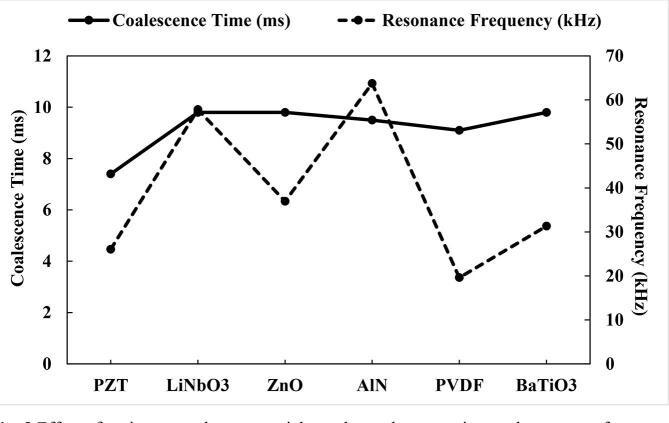
The order of the coalescence time followed PZT < PVDF < AlN < LiNbO3 < BaTiO3 < ZnO (Fig. 8). This is generally consistent with the synergy between the determined acoustic pressure magnitudes trend of the transducer materials as well as the acoustic impedance and piezoelectric coefficient. It is expected that as the acoustic pressure magnitude increases, the time taken for the coalescence of the droplets would reduce. Although the coalescence time of PZT is 1.7 times less than that of LiNbO3, the overall assessment which includes environmental impact makes Lithium niobate a possible substitute for PZT.
Fig. 8.
Effect of various transducer materials on the coalescence time and resonance frequency.
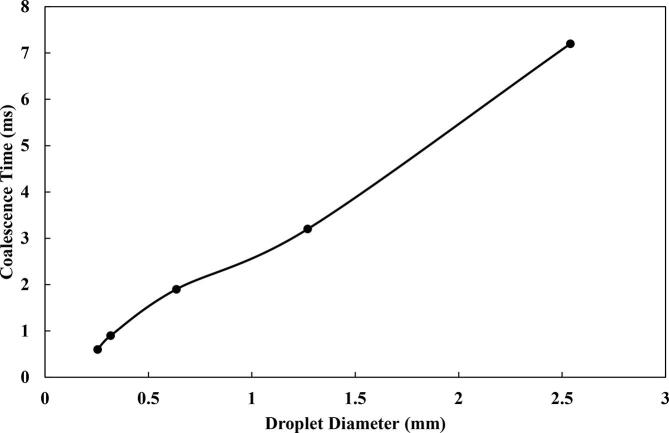
3.4.2. Droplet size
The influence of different initial droplet sizes on their coalescence in the oil phase was assessed. The studied droplet pairs have diameters of 0.254, 0.3175, 0.635, 1.27 and 2.54 × 10-3 m. The droplets were selected in order to be consistent with what is present in crude oil emulsions [29], [61]. It was observed that the size of the droplets has significant effect on their coalescence, with smaller droplets aggregating relatively faster (Fig. 9). The coalescence time which was 7.2 ms for D = 1.27 × 10-3 m reduced to 0.6 ms for D = 0.254 × 10-3 m. The increment in the coalescence time as the initial droplet diameter increases can be attributed to changes in the Weber number. In the study of the coalescence of Wang et al. [45], they highlighted that the rising of the Weber number at higher droplet sizes leads to delay in the recovery of the droplet to spherical forms after their starting deformation. This would aid in providing insight for the behavior of neighboring droplets during demulsification.
| (19) |
where is the initial droplet size, is the density, u is droplet relative velocity and is the surface tension.
Fig. 9.
Effect of the droplet size on the coalescence time.
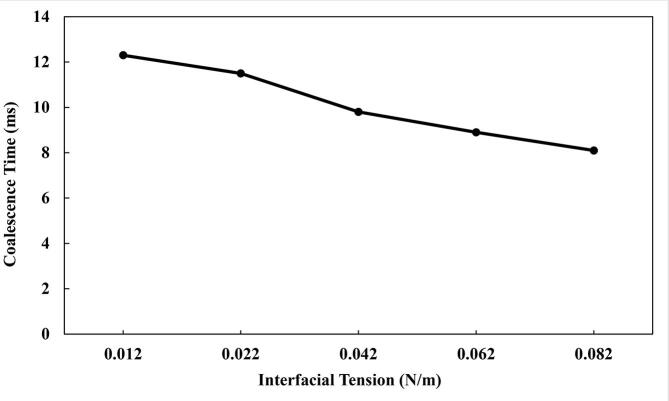
3.4.3. Interfacial tension
The effect of the interfacial tension on the US acoustic pressure and droplet coalescence in water-in-oil emulsion was assessed. This is important in determining optimal interfacial tension, significance of tension lowering emulsifiers and suitability of different crude oils for coalescence. Five different water–oil interface tension including 0.012, 0.022, 0.042, 0.062 and 0.082 N/m were investigated. These values are selected to have similarities with those reported in the literature for crude oil–water emulsions [29], [46], [47], [48], [49]. The results showed that the coalescence time reduced across the range of surface tensions evaluated (Fig. 10). For instance, the coalescence time reduced from 12.3 ms to 8.1 ms as the interfacial tension increased from 0.012 N/m to 0.082 N/m. This reduction can be attributed to the fact that lower interfacial tension produces emulsions which are relatively more stable. Hence, at lower interface tension between the water and crude oil, there was more resistance to the coalescence of the water droplets due to their improved emulsion stability. Similar impact of the interfacial tension obstruction of coalescence in emulsions has been reported elsewhere [22], [29]. For example, in the experimental study of Luo et al. [22], they reported that the dehydration efficiency (ξ) increased as the interfacial tension was raised from 4.79 to 10.35 mN/m at US frequencies of 25.8 kHz and 126.4 kHz. The demulsification efficiency denotes the effectiveness of the treatment method in the dehydration of the water-in-oil emulsion. It is defined as follows [50]:
| (20) |
where is the quantity of water after treatment and is the quantity of water before treatment (where measurements are in weight or volume basis).
Fig. 10.
Effect of the interfacial tension on the coalescence time.
Furthermore, the demulsification efficiencies increased from ∼25% to ∼68% and ∼16.6% to ∼56.5% at 25.8 kHz and 126.4 kHz, respectively. The findings of Luo et al. [22] further corroborate the validity of the developed coalescence model.
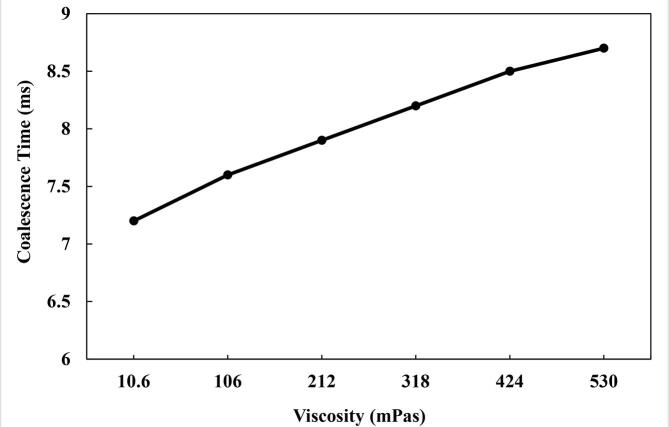
3.4.4. Viscosity
The impact of varying the viscosity of the crude oil on the coalescence of the water droplets in the oil phase was investigated. The viscosities studied ranged from 10.6 to 530 mPas in order to cover light, medium and heavy crude oils. It was observed that increasing the viscosities hindered the coalescence of the water droplets (Fig. 11). The coalescence time rose from 7.2 ms at 10.6 mPas to 8.7 ms at 530 mPas. The main causes for the behavior under varying viscosities could be the increment of the attenuation coefficient and flow inhibition as the viscosity increases. Majumdar et al. [51] reported that the attenuation coefficient has a direct relationship with the viscosity based on equation (20). The relationship was based on empirical assessment of the attenuation coefficient from their study, and provides acceptable congruence with the theoretical prediction of Stokes [52].
| (21) |
Fig. 11.
Effect of the crude oil viscosity on the coalescence time.
A similar observation to Majumdar et al. [51] was noted by Sutilov and Alferieff [53] where they showed that increasing viscosities raises the attenuation of US.
| (22) |
where is the attenuation coefficient, f is frequency, is the density, c is the speed of sound, is the dynamic viscosity and is the bulk viscosity.
Subsequently, as the USWs are attenuated more with rising viscosities, the effectiveness of US in droplet coalescence in viscous oils is significantly hindered. This lowering of the US impact would increase the time required for droplets coalescence. Another cause of higher coalescence time with rising viscosity is the resistance to the droplet motion in the oil phase through viscous flow resistance. This restricts the transfer and mechanical vibration which improves the coalescence of the water droplets [22].
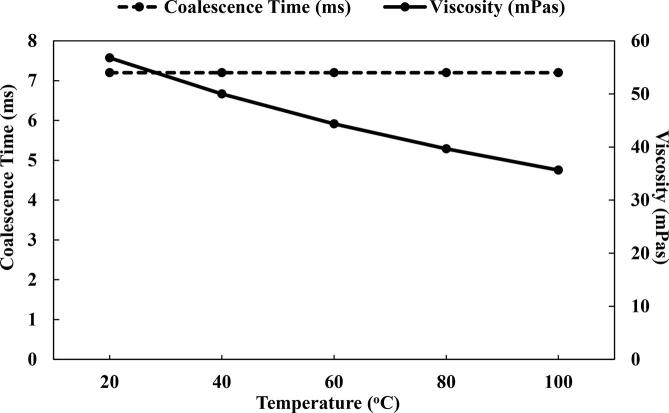
3.4.5. Temperature
The coalescence process was evaluated at elevated temperatures because some of the industrial oil operations such as refining occurs at increased temperatures. Hence, the effect of elevated temperatures on the coalescence of water droplets in oil was studied at 20, 40, 60, 80 and 100 °C. It was observed that the coalescence time was independent of the temperatures in the range studied. The coalescence was negligibly affected even with the reduction in the oil viscosity as the temperature increased (Fig. 12). For example, the increment of the temperature of the crude oil from 293.15 K to 373.15 K resulted in the lowering of the viscosity of oil from 56.80 to 35.64 mPas. This insignificant influence of the temperature on the coalescence could be due to the rather small difference between the viscosities at changing temperatures as well as the absence of emulsifiers. A similar finding is reported in the study of Atehortua et al. [38] where they showed that at 60 and 70 °C there was insignificant difference in the dewatering efficiency. The final mass percentages of water left after demulsification were 2.4% and 2.6% with US at 60 and 70 °C, respectively. Without the US, the remaining water content were 4.2 and 4.0% at 60 and 70 °C, respectively. Xu et al. [39] as well demonstrated that at 60 and 70 °C, there was minimal difference in the demulsification efficiency. In another study, Ye et al. [10] showed that for temperatures of 60, 70 and 80 °C, there was little difference in the dehydration. Their experiment, which was tested at different acoustic intensities (0–0.9 W/cm2) and irradiation times (0–20 min), consistently showed only slight differences. Although enhancement in the frequency of coalescence was mentioned by Bera et al. [30] at high temperature, this behavior cease to hold when the surfactant used was with concentrations lower than 0.01 mM. The hexadecane droplet coalescence in water continuous phase became erratic under low emulsifier amount. This shows that the improvement in the coalescence process described by Bera et al. [30] tends to rely significantly on the presence of surfactants.
Fig. 12.
Effect of the emulsion temperature on the coalescence time.
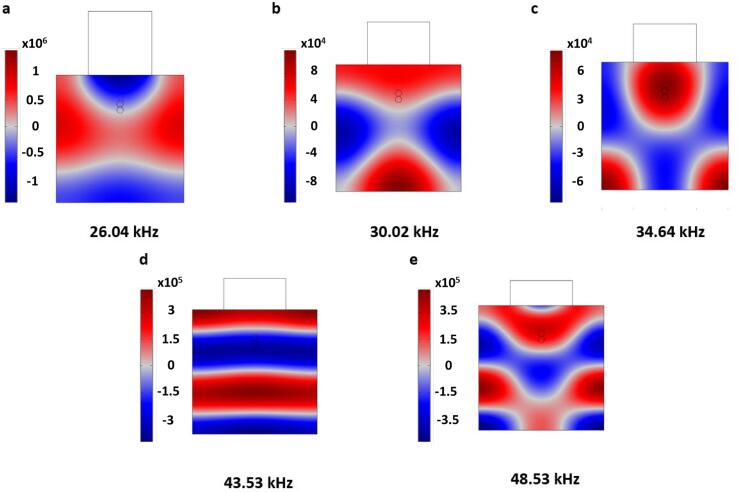
3.4.6. US frequency
The effect of US frequencies at 26.04, 30.02, 34.64, 43.53 and 48.53 kHz on the acoustic pressure and droplet coalescence was determined. These range of frequencies were utilized because many of the ultrasound transducer applications for coalescence of crude oil emulsions perform optimally at those values [11], [22], [37], [44]. Although the transducer diameter remained the same for all the frequencies studied, the transducer height reduced in order to account for the inverse relationship between frequency and piezoelectric material mass. It was observed that the acoustic pressure generally reduced and then increased thereafter as the frequency of the US increased (Fig. 13). At 26.04 kHz, a peak acoustic pressure of ∼1.15 × 106 Pa was obtained which continued to reduce to ∼6.23 × 104 at 34.64 kHz. However, the pressure rose thereafter to ∼3.79 × 105 Pa at 48.53 kHz. A similar observation was observed by Rashwan et al. [40] where the maximum acoustic pressure reduced between 30 and 70 kHz, and increased thereafter at 90 kHz. The US frequencies influences changes due to the reflected waves from hard wall boundaries [40]. Moreover, impacts could be complicated due to different wavelengths and periodic time at different US frequencies. The reduction in the maximum US pressure between 26.04 and 34.64 kHz could be attributed to attenuation effects described in Eqs. (18), (19). Since the attenuation coefficient has a direct relationship with the US frequency, the effect of the US could be lowered as the frequency increased. The different pressure distribution patterns with varying frequencies have been highlighted in some studies [40], [42], [43]. For example, in their numerical study, Hasnul Hadi et al. [42] reported varying pressure distribution pattern in ethanol at US frequencies of 20, 40 and 60 kHz. This behavior was attributed to wave interference at different frequencies. In an experimental hydrophone measurement, Leong et al. [43] showed that at US frequencies of 400 kHz and 2 MHz, different pressure distribution was detected in water in an ultrasound reactor chamber. The pressure magnitude varied at different positions within the chamber geometry. Moreover, Rashwan et al. [40] found similar occurrence with a sono-reactor containing distilled water at frequencies 20, 30, 40, 50, 70 and 90 kHz showing different pressure distributions. Although the above studies were focused on water and ethanol, they provide useful insights on the behavior of the pressure field under different frequencies.
Fig. 13.
Acoustic pressure for different US frequencies.
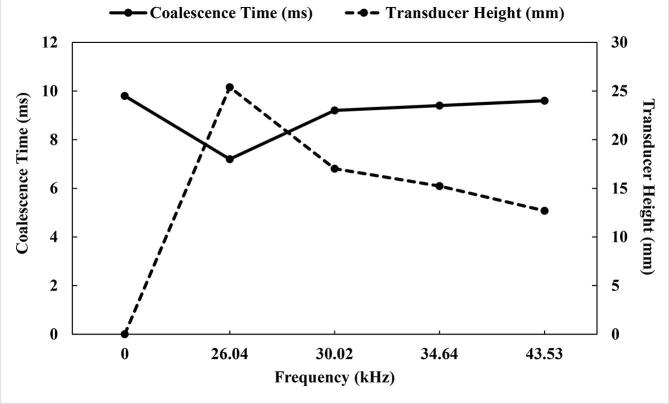
The US produced lengthier coalescence time at higher frequencies (Fig. 14). For example, the coalescence times at 26.04 kHz and 43.53 kHz were 7.2 and 9.6 ms, respectively. Xie et al. [37] suggested that demulsification is enhanced at small frequencies because of the small ratio of standing waves in the even US fields as well as elevated distance of US effective radiation. Similar findings were reported by Wang et al. [21] that as the US frequency increased, dehydration performance of water-in-oil emulsion improved. In their experiment, whilst ∼95% demulsification efficiency was reached at 10 kHz, this dropped further to ∼92% and ∼91.2% at US frequencies of ∼30 kHz and ∼36.5 kHz, respectively. Luo et al. [22] showed the same trend in their experimental study with a frequency of 25.8 kHz providing better dehydration performance than a frequency of 126.4 kHz. Moreover, the experimental findings and model estimates of Pangu and Feke [62] revealed that the volume averaged radius of the binary droplet increased with time at US frequencies of 0.525 and 1.69 MHz. However, the model prediction showed that the lower frequency (0.525 MHz) produced elevated volume radius sizes as compared to the higher frequencies (1.69 MHz). This agrees with the observation in this study as larger coalesced drops at lower frequency (0.525 MHz) is an indication of better coalescence. Similar trend was observed in their experiments below 120 s, after which the slower rate of coalescence at lower frequency resulted in increased volume sizes between 120 and 300 s.
Fig. 14.
Effect of the US frequency on the coalescence time and transducer height.
3.4.7. Ultrasound power
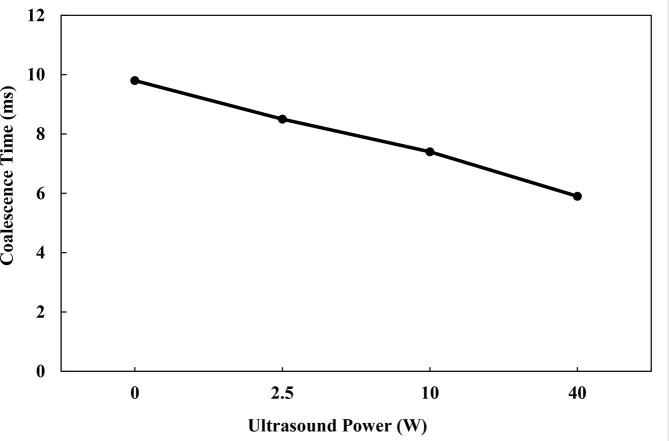
Four ultrasound power (0, 2.5, 10 and 40 W) levels were considered in order to determine their influence on the coalescence process. It could be observed that the coalescence time was lower with the usage of US as compared to the case without the transducer. This shows that the US waves were important in lowering the coalescence time required. This phenomenon has been confirmed experimentally in other studies. Studies such as Luo et al. [22], Aterhortua et al. [38], Antes et al. [11], Xu et al. [39] and Xie et al. [37] have demonstrated the significance of US in hastening the coalescence process. In this work, the coalescence time was reduced from 8.5 ms to 5.9 ms as the applied power was increased between 2.5 and 40 W (Fig. 15). This could be due to the increase in the secondary acoustic force as the intensity of the US was increased. The secondary acoustic force influences the interaction between droplets and could impact their coalescence and dewatering. Different experimental reports on the synergistic effect of the US could be found elsewhere [8], [21], [37], [44]. Ye et al. [10] showed that the coalescence was improved as the acoustic intensities rose up to 0.38 W/cm2. The residual water content after treatment was lowered by 66.67% at 60 °C. Yang et al. [8] determined that the demulsification efficiency reached about 98% as the US power increased to 100 W. Yi et al. [44] reported that for 50, 100 and 150 W power, the coalescence was enhanced as the power was elevated. Pangu and Feke [64] showed that the oil collection efficiency was 62, 75 and 80% for the applied ultrasound power of 6.3, 25.8 and 47.2 W, respectively. However, the demulsification process was for vegetable oil droplets in water. Xie et al. [37] and Wang et al. [21] found similar increasing trend of dehydration as the US power per unit area was raised within a specified range.
Fig. 15.
Effect of the transducer power on the coalescence time.
4. Conclusion
In this study, a numerical assessment of the coalescence of water droplets in oil phase was conducted. In particular, the effect of transducer material, initial droplet diameter (0.05–0.2 in), interfacial tension (0.012–0.082 N/m), dynamic viscosity (10.6–530 mPas), temperature (20–100C), US frequency (26.04–43.53 kHz) and applied transducer power (2.5–40 W) were considered. The materials assessed include PZT, LiNbO3, ZnO, AlN, PVDF, and BaTiO3. The numerical simulation of the binary droplet coalescence showed good agreement with previous experimental data. The US implementation produced enhanced coalescence as compared to gravitational settling. Moreover, the results showed that the coalescence time reduced across the range of interfacial tensions which were considered. This reduction can be attributed to the fact that lower interfacial tension produces emulsions which are relatively more stable. Hence, at lower interface tension between the water and crude oil, there was more resistance to the coalescence of the water droplets due to their improved emulsion stability. The increment of the Weber number at higher droplet sizes leads to a delay in the recovery of the droplet to spherical forms after their starting deformation. At different ultrasound (US) frequencies and transducer materials, a variation in the acoustic pressure distribution was observed. Possible attenuation of the US waves, and the subsequent inhibitive coalescence effect under various US frequencies and viscosities, was discussed. Nonetheless, the quick coalescence showed that US can be applied for both static as well as to moving emulsion phase. This has the advantage to eliminate cumbersome storage tanks and to consider placing the US probes directly on the carrying pipelines, in contact with the passing emulsion fluid or using some acoustic matching layers to proceed with inline demulsification. As future work, different flow regimes with different droplets velocities will be considered to assess their respective effects on oil–water demulsification. In addition, the usage of multiple ultrasonic probes as well as high intensity focused ultrasonic probes should be investigated. The coalescence of the binary droplets could be utilized to predict the demulsification process with multiple or enlarged droplets. Descriptions of the scaling of the droplet coalescence could be found in the works of Boxall et al. [59], Hamedani [60] and Leister et al. [41].
CRediT authorship contribution statement
Idowu Adeyemi: Formal analysis, Methodology, Software, Writing – original draft, Writing – review & editing. Mahmoud Meribout: Conceptualization, Methodology, Writing – review & editing. Lyes Khezzar: Conceptualization, Methodology, Writing – review & editing. Nabil Kharoua: Methodology, Writing – review & editing. Khalid AlHammadi: Conceptualization, Methodology.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgements
The authors acknowledge the support from Khalifa University, United Arab Emirates through research grant number CIRA-2020-086.
References
- 1.Wong S.F., Lim J.S., Dol S.S. Crude oil emulsion: A review on formation, classification and stability of water-in-oil emulsions. J. Pet. Sci. and Eng. 2015;135:498–504. [Google Scholar]
- 2.Abramova A., Abramov V., Bayazitov V., Gerasin A., Pashin D. Ultrasonic technology for enhanced oil recovery. Engineering. 2014;6(4):177–184. [Google Scholar]
- 3.Shehzad F., Hussein I.A., Kamal M.S., Ahmad W., Sultan A.S., Nasser M.S. Polymeric surfactants and emerging alternatives used in the demulsification of produced water: A review. Polym. Rev. 2018;58(1):63–101. [Google Scholar]
- 4.Abdulredha M.M., Aslina H.S., Luqman C.A. Overview on petroleum emulsions, formation, influence and demulsification treatment techniques. Arab. J. Chem. 2020;13(1):3403–3428. [Google Scholar]
- 5.Nouvelles, I. E. (2011). Water in fuel production-oil production and refining. Technical report. Available: http://www.ifpenergiesnouvelles. com/content/download/70601/1513892/version/2/file/Panorama2011_11-VA_Eau-Production-Carburants.pdf.
- 6.Umar A.A., Saaid I.B.M., Sulaimon A.A., Pilus R.B.M. A review of petroleum emulsions and recent progress on water-in-crude oil emulsions stabilized by natural surfactants and solids. J. Pet. Sci. Eng. 2018;165:673–690. [Google Scholar]
- 7.Pedrotti M.F., Enders M.S., Pereira L.S., Mesko M.F., Flores E.M., Bizzi C.A. Intensification of ultrasonic-assisted crude oil demulsification based on acoustic field distribution data. Ultrason. Sonochem. 2018;40:53–59. doi: 10.1016/j.ultsonch.2017.03.056. [DOI] [PubMed] [Google Scholar]
- 8.Yang X.G., Tan W., Tan X.F. Demulsification of crude oil emulsion via ultrasonic chemical method. Pet. Sci. Technol. 2009;27(17):2010–2020. [Google Scholar]
- 9.Nasiri H.G., Mosavian M.H., Kadkhodaee R. Demulsification of gas oil/water emulsion via high-intensity ultrasonic standing wave. J. Dispers. Sci. Technol. 2013;34(4):483–489. [Google Scholar]
- 10.Ye G., Lu X., Han P., Peng F., Wang Y., Shen X. Application of ultrasound on crude oil pretreatment. Chem. Eng. Process. 2008;47(12):2346–2350. [Google Scholar]
- 11.Antes F.G., Diehl L.O., Pereira J.S., Guimarães R.C., Guarnieri R.A., Ferreira B.M., Flores E.M. Effect of ultrasonic frequency on separation of water from heavy crude oil emulsion using ultrasonic baths. Ultrason. Sonochem. 2017;35:541–546. doi: 10.1016/j.ultsonch.2016.03.031. [DOI] [PubMed] [Google Scholar]
- 12.Hamidi H., Mohammadian E., Asadullah M., Azdarpour A., Rafati R. Effect of ultrasound radiation duration on emulsification and demulsification of paraffin oil and surfactant solution/brine using Hele-shaw models. Ultrason. Sonochem. 2015;26:428–436. doi: 10.1016/j.ultsonch.2015.01.009. [DOI] [PubMed] [Google Scholar]
- 13.Akbarian Kakhki N., Farsi M., Rahimpour M.R. Effect of current frequency on crude oil dehydration in an industrial electrostatic coalescer. J. Taiwan Inst. Chem. Eng. 2016;67:1–10. [Google Scholar]
- 14.Martínez-Palou R., Cerón-Camacho R., Chávez B., Vallejo A.A., Villanueva-Negrete D., Castellanos J., Karamath J., Reyes J., Aburto J. Demulsification of heavy crude oil-in-water emulsions: A comparative study between microwave and thermal heating. Fuel. 2013;113:407–414. [Google Scholar]
- 15.Wu J., Wei W., Li S., Zhong Q., Liu F., Zheng J., Wang J. The effect of membrane surface charges on demulsification and fouling resistance during emulsion separation. J. Membr. Sci. 2018;563:126–133. [Google Scholar]
- 16.Saad M.A., Kamil M., Abdurahman N.H., Yunus R.M., Awad O.I. An overview of recent advances in state-of-the-art techniques in the demulsification of crude oil emulsions. Processes. 2019;7(7):470. [Google Scholar]
- 17.Ezzat A.O., Atta A.M., Al-Lohedan H.A., Abdullah M.M., Hashem A.I. Synthesis and application of poly (ionic liquid) based on cardanol as demulsifier for heavy crude oil water emulsions. Energy Fuels. 2018;32(1):214–225. [Google Scholar]
- 18.Wen Y., Cheng H., Lu L.J., Liu J., Feng Y., Guan W., Zhou Q., Huang X.F. Analysis of biological demulsification process of water-in-oil emulsion by Alcaligenes sp. S-XJ-1. Bioresour. Technol. 2010;101(21):8315–8322. doi: 10.1016/j.biortech.2010.05.088. [DOI] [PubMed] [Google Scholar]
- 19.Singh A., Van Hamme J.D., Ward O.P. Surfactants in microbiology and biotechnology: Part 2. Application aspects. Biotechnol. Adv. 2007;25:99–121. doi: 10.1016/j.biotechadv.2006.10.004. [DOI] [PubMed] [Google Scholar]
- 20.Roostaie T., Farsi M., Rahimpour M.R., Biniaz P. Performance of biodegradable cellulose based agents for demulsification of crude oil: Dehydration capacity and rate. Sep. Purif. Technol. 2017;179:291–296. [Google Scholar]
- 21.Wang Z., Gu S., Zhou L. Research on the static experiment of super heavy crude oil demulsification and dehydration using ultrasonic wave and audible sound wave at high temperatures. Ultrason. Sonochem. 2018;40:1014–1020. doi: 10.1016/j.ultsonch.2017.08.037. [DOI] [PubMed] [Google Scholar]
- 22.Luo X., Gong H., Yin H., He Z., He L. Optimization of acoustic parameters for ultrasonic separation of emulsions with different physical properties. Ultrason. Sonochem. 2020;68:105221. doi: 10.1016/j.ultsonch.2020.105221. [DOI] [PubMed] [Google Scholar]
- 23.Sadatshojaie A., Wood D.A., Jokar S.M., Rahimpour M.R. Applying ultrasonic fields to separate water contained in medium-gravity crude oil emulsions and determining crude oil adhesion coefficients. Ultrason. Sonochem. 2021;70:105303. doi: 10.1016/j.ultsonch.2020.105303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Khajehesamedini A., Sadatshojaie A., Parvasi P., Rahimpour M.R., Naserimojarad M.M. Experimental and theoretical study of crude oil pretreatment using low-frequency ultrasonic waves. Ultrason. Sonochem. 2018;48:383–395. doi: 10.1016/j.ultsonch.2018.05.032. [DOI] [PubMed] [Google Scholar]
- 25.Xu Z. Numerical simulation of the coalescence of two bubbles in an ultrasound field. Ultrason. Sonochem. 2018;49:277–282. doi: 10.1016/j.ultsonch.2018.08.014. [DOI] [PubMed] [Google Scholar]
- 26.Mohsin M., Meribout M. Oil–water de-emulsification using ultrasonic technology. Ultrason. Sonochem. 2015;22:573–579. doi: 10.1016/j.ultsonch.2014.05.014. [DOI] [PubMed] [Google Scholar]
- 27.COMSOL. CFD Module User’s Guide. (2017).
- 28.Lin Y., Skjetne P., Carlson A. A phase field model for multiphase electro-hydrodynamic flow. Int. J. Multiphase Flow. 2012;45:1–11. [Google Scholar]
- 29.Luo X., Cao J., He L., Wang H., Yan H., Qin Y. An experimental study on the coalescence process of binary droplets in oil under ultrasonic standing waves. Ultrason. Sonochem. 2017;34:839–846. doi: 10.1016/j.ultsonch.2016.07.024. [DOI] [PubMed] [Google Scholar]
- 30.Bera B., Khazal R., Schroën K. Coalescence dynamics in oil-in-water emulsions at elevated temperatures. Sci. Rep. 2021;11(1):1–10. doi: 10.1038/s41598-021-89919-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Eggers J., Lister J.R., Stone H.A. Coalescence of liquid drops. J. Fluid Mech. 1999;401:293–310. [Google Scholar]
- 32.Vrij A. Possible mechanism for the spontaneous rupture of thin, free liquid films. Discuss. Faraday Soc. 1966;42:23–33. [Google Scholar]
- 33.Stein H.N. The drainage of free liquid films. Colloids Surf. A Physicochem. Eng. Aspects. 1993;79(1):71–80. [Google Scholar]
- 34.Yamashita Y., Miyahara R., Sakamoto K. Elsevier Inc.; Amsterdam, The Netherlands: 2017. Emulsion and emulsification technology. Cosmetic Science and Technology: Theoretical Principles and Applications; pp. 489–506. [Google Scholar]
- 35.Pons R. Elsevier; Amsterdam: 2000. Polymeric Surfactants as Emulsion Stabilizers. Amphiphilic Block Copolymers: Self-Assembly and Applications; pp. 409–422. [Google Scholar]
- 36.Kuroiwa Y., Kim S., Fujii I., Ueno S., Nakahira Y., Moriyoshi C., Sato Y., Wada S. Piezoelectricity in perovskite-type pseudo-cubic ferroelectrics by partial ordering of off-centered cations. Nat. Commun. Mater. 2020;1(1):1–8. [Google Scholar]
- 37.Xie W., Li R., Lu X. Pulsed ultrasound assisted dehydration of waste oil. Ultrason. Sonochem. 2015;26:136–141. doi: 10.1016/j.ultsonch.2015.03.004. [DOI] [PubMed] [Google Scholar]
- 38.Atehortúa C.M.G., Pérez N., Andrade M.A.B., Pereira L.O.V., Adamowski J.C. Water-in-oil emulsions separation using an ultrasonic standing wave coalescence chamber. Ultrason. Sonochem. 2019;57:57–61. doi: 10.1016/j.ultsonch.2019.04.043. [DOI] [PubMed] [Google Scholar]
- 39.Xu X., Cao D., Liu J., Gao J., Wang X. Research on ultrasound-assisted demulsification/dehydration for crude oil. Ultrason. Sonochem. 2019;57:185–192. doi: 10.1016/j.ultsonch.2019.05.024. [DOI] [PubMed] [Google Scholar]
- 40.Rashwan S.S., Dincer I., Mohany A. Investigation of acoustic and geometric effects on the sonoreactor performance. Ultrason. Sonochem. 2020;68:105174. doi: 10.1016/j.ultsonch.2020.105174. [DOI] [PubMed] [Google Scholar]
- 41.Leister N., Yan C., Karbstein H.P. Oil Droplet Coalescence in W/O/W Double Emulsions Examined in Models from Micrometer-to Millimeter-Sized Droplets. Colloids and Interfaces. 2022;6(1):12. [Google Scholar]
- 42.Hadi N.A.H., Ahmad A., Oladokun O. E3S Web of Conferences. EDP Sciences; 2019. Modelling pressure distribution in sonicated ethanol solution using COMSOL simulation; p. 02003. [Google Scholar]
- 43.Leong T., Coventry M., Swiergon P., Knoerzer K., Juliano P. Ultrasound pressure distributions generated by high frequency transducers in large reactors. Ultrasonics sonochemistry. 2015;27:22–29. doi: 10.1016/j.ultsonch.2015.04.028. [DOI] [PubMed] [Google Scholar]
- 44.Yi M., Huang J., Wang L. Research on crude oil demulsification using the combined method of ultrasound and chemical demulsifier. J. Chem. 2017;2017:1–7. [Google Scholar]
- 45.Wang Y., Qian L., Chen Z., Zhou F. Coalescence of binary droplets in the transformer oil based on small amounts of polymer: effects of initial droplet diameter and collision parameter. Polymers. 2020;12(9):2054. doi: 10.3390/polym12092054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Nikseresht S., Riazi M., Amani M.J., Farshchi Tabrizi F. Prediction of oil/water interfacial tension containing ionic surfactants. Colloid Interface Sci. Commun. 2020;34:100217. [Google Scholar]
- 47.Zhang, Z., Stephens, A., & Wang, J. (2020). Temperature Effect on Interactions of Oil Droplet with Water-wetted Shale Kerogen at Reservoir Temperatures: Linear Relationships between Temperature, Free Energy, and Contact Angle. arXiv preprint arXiv:2007.09741.
- 48.Yongmao H., Mingjing L., Chengshun D., Jianpeng J., Yuliang S., Guanglong S. Experimental investigation on oil enhancement mechanism of hot water injection in tight reservoirs. Open Phys. 2016;14(1):703–713. [Google Scholar]
- 49.Abdelrahim M.A., Rao D.N. Wiley Online Books; 2014. Measurement of interfacial tension in hydrocarbon/water/dispersant systems at deepwater conditions. Oil Spill Remediat. [Google Scholar]
- 50.Luo X., Gong H., Cao J., Yin H., Yan Y., He L. Enhanced separation of water-in-oil emulsions using ultrasonic standing waves. Chem. Eng. Sci. 2019;203:285–292. [Google Scholar]
- 51.Majumdar S., Kumar P.S., Pandit A.B. Effect of liquid-phase properties on ultrasound intensity and cavitational activity. Ultrason. Sonochem. 1998;5(3):113–118. doi: 10.1016/s1350-4177(98)00019-4. [DOI] [PubMed] [Google Scholar]
- 52.Stokes G.G. On the theories of the internal friction of fluids in motion and of the equilibrium and motion of elastic solids. Trans. Cambridge Philos. Soc. 1845;8:287–319. [Google Scholar]
- 53.Shutilov V.A., Alferieff M.E. CRC Press; 2020. Fundamental Physics of Ultrasound. [Google Scholar]
- 54.Papadakis N.M., Stavroulakis G.E. Proceedings of the Euronoise. 2018. Effect of mesh size for modeling impulse responses of acoustic spaces via finite element method in the time domain. [Google Scholar]
- 55.Minin I., Minin O., Siemens E., Mehtiyev A.D., Syryamkin V.I., Yurchenko A.V. Mesoscale acoustical cylindrical Superlens. MATEC Web Conf. 2018;155:01029. [Google Scholar]
- 56.K.K. Amireddy, K. Balasubramaniam, P. Rajagopal, Holey-structured metamaterial lens for subwavelength resolution in ultrasonic characterization of metallic components. Appl. Phys. Lett., 108(22) (2016) 224101.
- 57.Makinde W., Favretto-Cristini N., De Bazelaire E. Numerical modelling of interface scattering of seismic wavefield from a random rough interface in an acoustic medium: comparison between 2D and 3D cases. Geophys. Prospect. 2005;53(3):373–397. [Google Scholar]
- 58.COMSOL. Acoustic Module User’s Guide. (2017).
- 59.Boxall J.A., Koh C.A., Sloan E.D., Sum A.K., Wu D.T. Droplet size scaling of water-in-oil emulsions under turbulent flow. Langmuir. 2012;28(1):104–110. doi: 10.1021/la202293t. [DOI] [PubMed] [Google Scholar]
- 60.Hamedani B.K. Université de Lyon; 2019. Design, Scale-up and Optimization of Double Emulsion Processes. Doctoral dissertation. [Google Scholar]
- 61.Siva S.P., Kow K.W., Chan C.H., Tang S.Y., Ho Y.K. Prediction of droplet sizes for oil-in-water emulsion systems assisted by ultrasound cavitation: transient scaling law based on dynamic breakup potential. Ultrason. Sonochem. 2019;55:348–358. doi: 10.1016/j.ultsonch.2018.12.040. [DOI] [PubMed] [Google Scholar]
- 62.Pangu G.D., Feke D.L. Kinetics of ultrasonically induced coalescence within oil/water emulsions: modeling and experimental studies. Chem. Eng. Sci. 2009;64(7):1445–1454. [Google Scholar]
- 63.Pangu G.D., Feke D.L. Droplet transport and coalescence kinetics in emulsions subjected to acoustic fields. Ultrasonics. 2007;46(4):289–302. doi: 10.1016/j.ultras.2007.03.004. [DOI] [PubMed] [Google Scholar]
- 64.Pangu G.D., Feke D.L. Acoustically aided separation of oil droplets from aqueous emulsions. Chem. Eng. Sci. 2004;59(15):3183–3193. [Google Scholar]
- 65.Batchelor G.K. Sedimentation in a dilute polydisperse system of interacting spheres. Part 1. General theory. J. Fluid Mech. 1982;119:379–408. [Google Scholar]
- 66.Ronchi R.P., Negris L., Melo B.N., Pereira L.S., Vicente M.A., Flores E.M., Santos M.D.F.P. Removal of oil from synthetic heavy crude oil-in-water emulsions by the association of glass raschig rings and ultrasound. J. Dispers. Sci. Technol. 2021;43(1):22–32. [Google Scholar]
- 67.Antes F.G., Diehl L.O., Pereira J.S., Guimarães R.C., Guarnieri R.A., Ferreira B.M., Dressler V.L., Flores E.M. Feasibility of low frequency ultrasound for water removal from crude oil emulsions. Ultrason. Sonochem. 2015;25:70–75. doi: 10.1016/j.ultsonch.2015.01.003. [DOI] [PubMed] [Google Scholar]