A Chirality-Based Quantum Leap

Abstract

There is increasing interest in the study of chiral degrees of freedom occurring in matter and in electromagnetic fields. Opportunities in quantum sciences will likely exploit two main areas that are the focus of this Review: (1) recent observations of the chiral-induced spin selectivity (CISS) effect in chiral molecules and engineered nanomaterials and (2) rapidly evolving nanophotonic strategies designed to amplify chiral light–matter interactions. On the one hand, the CISS effect underpins the observation that charge transport through nanoscopic chiral structures favors a particular electronic spin orientation, resulting in large room-temperature spin polarizations. Observations of the CISS effect suggest opportunities for spin control and for the design and fabrication of room-temperature quantum devices from the bottom up, with atomic-scale precision and molecular modularity. On the other hand, chiral–optical effects that depend on both spin- and orbital-angular momentum of photons could offer key advantages in all-optical and quantum information technologies. In particular, amplification of these chiral light–matter interactions using rationally designed plasmonic and dielectric nanomaterials provide approaches to manipulate light intensity, polarization, and phase in confined nanoscale geometries. Any technology that relies on optimal charge transport, or optical control and readout, including quantum devices for logic, sensing, and storage, may benefit from chiral quantum properties. These properties can be theoretically and experimentally investigated from a quantum information perspective, which has not yet been fully developed. There are uncharted implications for the quantum sciences once chiral couplings can be engineered to control the storage, transduction, and manipulation of quantum information. This forward-looking Review provides a survey of the experimental and theoretical fundamentals of chiral-influenced quantum effects and presents a vision for their possible future roles in enabling room-temperature quantum technologies.

Chiral matter broadly describes structures for which left- or right-handed mirror images are nonsuperimposable, or, equivalently, that lack improper rotation axes. Chiral matter offers opportunities for the exquisite control of electron and spin transport due to extraordinary optical, electronic, and magnetic properties that depend on the structure’s handedness. Importantly, these properties are often observed at or near room temperature, which suggests that quantum devices based on chiral matter and fields have the potential to operate at similar practical temperatures if properly designed.

Questions about how chirality can be rationally incorporated for quantum control have been catalyzed by rapidly expanding research frontiers that focus on chiral systems spanning single molecules to hierarchically assembled nanoparticles and metamaterials. These questions are driven in particular by improvements in our understanding of electron spin-dependent interactions with chiral molecules, described by the chiral-induced spin selectivity (CISS) effect,^1,2 as well as advances in amplifying chiral light–matter interactions with nanophotonic platforms^3,4 or through self-assembly.⁵

In this context, it is exciting to ask what experimental degrees of freedom that chirality in configuration, in electronic structure, and in electromagnetic radiation provide in the context of quantum information processing. These degrees of freedom may be categorized by considering an accessible experimental space that is composed of three axes built by matter, probes, and their interactions (Figure 1). Chiral or achiral matter can be characterized using chiral or achiral experimental probes, the latter of which is subsequently transduced into a measurable quantity. The most obvious examples of a chiral probe would be circularly polarized light used for photoexcitation or an electron beam with well-defined helicity. The third axis of the experimental space concerns the matter–probe interaction itself, which can be characterized by a degree of “quantumness” that either preserves or destroys coherent properties in the system under study. Quantum backaction and measurement-induced decoherence can strongly influence measurement outcomes by modifying or suppressing responses to a detection protocol when attempting to measure, for example, spin precession.⁶⁻⁸ It remains to be seen whether the chiral character of matter and of experimental probes influence these properties. Thus, future research that aims to elucidate whether chirality may preserve or enhance coherent properties in charge and spin transport or in information transduction between electrons and photons will require measurement schemes that enable smooth tuning of the interaction strength.⁹ With this range of probe–matter interaction enhancement opportunities, we highlight two key questions in the context of chirality: (1) what signal transduction efficiencies are possible? and (2) to what extent can coherence be preserved, both during the transduction, and also while propagating between systems once induced?

Figure 1.

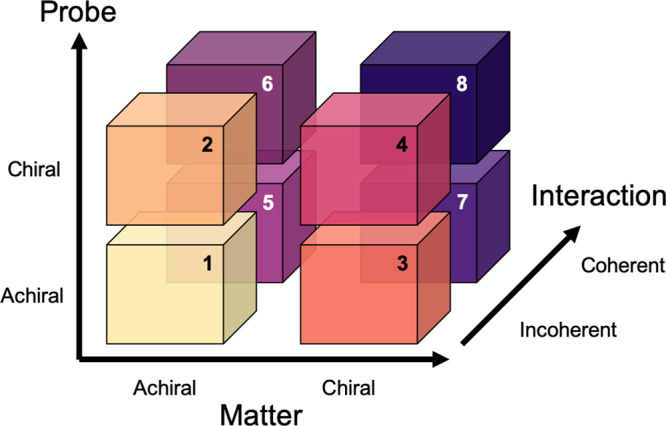
Chiral experimenter’s space. The matter under study and the probe (e.g., electromagnetic fields) can be either chiral or nonchiral. We expect different interaction strengths and rules to be valid in each “box”. A third interaction axis points to the fact that matter–probe interactions could be classical (incoherent) (boxes 1–4) or, in principle, preserve coherences (boxes 5–8).

In technological quantum devices, achieving and reading out spin polarization typically requires a sophisticated degree of quantum control. This control is most often achieved via engineered electromagnetic excitation in the initialization of a pure spin state. Alternatively, unveiling the mechanisms behind electron spin transport in chiral molecules and understanding the possible quantum mechanical contributions to the CISS effect may enable chiral molecular systems to be used for methods to prepare spin-polarized electron states.¹⁰ It is therefore necessary to elucidate the roles of coherence in spin selectivity. These roles include spatial coherence of charge transport through a helical electrostatic potential, that is, in tunneling vs hopping regimes, as well as coherence between spin states or excited electronic states.

Likewise, ways to transduce information encoded in electron spins to and from photon spin and orbital angular momenta could be made possible by tailoring chiral electromagnetic fields with nanoscale confinement. Moreover, chiral photonic circuits can be designed to engineer photon propagation and emission directions.^11,12 From a chemistry perspective, confinement enables enhancement in enantioselective rates of absorption of circularly polarized light and other light–matter interactions mediated by chiral molecules positioned within the near fields of these nanostructures. This localization makes possible the manipulation of quantized states and superpositions at the single-electron and single-photon levels in chiral molecular systems.

In this Review, we highlight the potential of leveraging chiral matter and fields for as yet untapped applications in the quantum sciences. We detail how chiral matter presents advantages for the scalability and flexibility of molecular architectures interfaced with low-dimensional materials; the operation of quantum devices at room temperature and in noisy photonic, phononic, and electronic environments; and the advance of investigations into the emergent field of quantum biology. We first review recent theoretical and experimental advances in chiral electron–matter and light interactions, and engineered chiral systems, before offering perspectives on how these properties can be used to investigate nontrivial quantum effects in chiral materials as follows:

• Chiral-Induced Spin Selectivity: Recent Advances

• Chiral Light–Matter Interactions

• Leveraging Chirality in the Quantum Sciences

• Future Outlook and Conclusions

Table 1. Glossary of Key Terms.

term	description	ref
chiral-induced spin selectivity (CISS)	preference for electron spin orientation and propagation direction in charge transport or transmission through left- vs right-handed nonsuperimposable molecules	(1)
spin selectivity (S) or spin polarization (P)	S (or P) = (I+ – I–)/(I+ + I–), where I+ and I– are the intensity of the experimental measurables, for example, current, rate constant, etc., for the spin oriented parallel and antiparallel to the electrons’ velocity	(1)
spin–orbit (SO) interactions (SOI) or spin–orbit coupling (SOC)	interactions between the electron spin and the orbital motion inside a potential; in CISS, the structural chirality causes a significant coupling between the electron spin and the angular momentum despite the light atoms	(13)
magnetic exchange effect	short-range interaction between electrons imposed by symmetry requirements on spin state	(14)
optical chirality density	describes the local handedness of an electromagnetic field that depends on uniquely defined and physically observable field quantities	(15, 16)
chirality transfer or imprinting	phenomenon by which achiral matter acquires chiral–optical properties	(17)

Chiral-Induced Spin Selectivity: Recent Advances

We review recent developments regarding the CISS effect, encompassing both experimental and theoretical findings. Among experimental efforts, we will discuss spin-polarized charge transport, spin–orbit coupling (SOC), magnetic exchange interactions, temperature dependence, biological implications, enantioselective chemical reactions, and chiral crystals. On the theoretical side, we will review symmetry breaking, molecular spin–orbit and intermolecular interactions, dipolar effects, orbital polarization, magnetic exchange interactions, vibrational contributions to spin-dependent transport, and the role of coherence.

Electron-spin-dependent and enantioselective interactions between electrons and chiral molecules are described by the CISS effect. In electron transport through chiral molecules or nanoscopic structures with broken inversion symmetry, a particular component of electron spin is favored with respect to the direction of charge propagation and chirality axes. This effect is described generally as spin selectivity. More specifically, CISS can be physically understood as an asymmetric electron scattering process in a chiral potential that has a strong dependence on spin–orbit interactions (SOIs), and where both spatial inversion and time reversal symmetries are broken (see below). This spin selectivity survives the inclusion of many-electron interactions and can coexist with other magnetic responses, including triplet radical formation, interstate crossing, and singlet fission, which provide fertile ground for spin manipulation. Most recently, experimental and theoretical work has suggested that the CISS effect is closely related to exchange interactions, which play a central role in molecular recognition and chirality-induced effects on magnetic surfaces.

The CISS effect has been observed in a range of experiments and for diverse chiral molecules and materials in electron transfer (ET), electron transport, and bond polarization through chiral structures. Despite the variety of structures studied, similar experimental aspects of spin selectivity have been consistently found in different measurements. For example, the dependence of asymmetry in spin-dependent transport through chiral molecules on molecular (helical) length is well-established, with increasing length corresponding to higher spin polarization of transmitted electrons.¹⁸ In addition, for commonly studied biologically relevant molecules, including DNA, peptides, and proteins that host secondary and tertiary structures, the handedness of higher order structural motifs appears to dominate over the chirality of individual subunits (i.e., amino acids and sugars) in defining the sign of the spin selectivity. Finally, the CISS effect is repeatedly observed at room temperature and ambient conditions, which is an exciting attribute that is particularly noteworthy for potential quantum technologies.

Many questions remain that must be addressed to advance our understanding of the CISS effect and how it may be leveraged for the manipulation of quantum information. Key remaining questions include: Under what conditions do chiral molecules act as electron spin filters vs electron spin polarizers (i.e., in inducing spin flips)? What are the electronic and magnetic contributions of symmetry constraints in enantioselective interactions? What roles do spatial and spin coherences play in chiral spin-dependent interactions? What is the biological significance of the CISS effect? Is there a predictive, unifying, and experimentally tractable model of electron spin-dependent transport through a chiral molecule? Experimental and theoretical advances are described below that have taken steps toward answering some of these questions. We highlight recent findings that identify measurement or modeling constraints for the detection of the CISS effect, which provide insight into mechanisms of CISS, and that provide practical and advantageous frameworks to test the contributions of nontrivial quantum effects to CISS.

Experimental Highlights

The number of experimental reports on the CISS effect has rapidly grown over the past decade, and the number of research groups around the world conducting studies in this area is increasing. The many different experimental configurations used to characterize spin selectivity include over-the-barrier transmission of photoelectrons through chiral films,¹⁹⁻²² conduction through single or few chiral molecules measured via conductive scanning probe techniques,²³⁻²⁵ electrochemistry with functionalized ferromagnetic electrodes,²⁶⁻²⁸ Hall devices to measure spin currents,²⁹⁻³¹ and photoluminescence.³²⁻³⁴ In nearly all experiments, observation of the CISS effect is validated by measuring the differences between a figure of merit (e.g., current, voltage, photoelectron counts, fluorescence intensity, etc.) in a chiral system upon reversal of magnetization orientation of an external element (e.g., a ferromagnetic substrate or scanning probe tip, which serves as a source or sink of spin-polarized electrons), upon substitution of opposite molecular enantiomers, when possible, or by changing the incident light between left- and right-handed circular polarization in experiments that exploit photoexcitation. Often, the figure of merit is reported as “spin polarization”. By conventional measures, the spin polarization along a particular axis is defined as P = (N_α – N_β)/(N_α + N_β), where N_α (N_β) is the number of electron spin measurements that would yield the eigenvalue +ℏ/2 (−ℏ/2), and N_α + N_β is the total number of measurements. With the exception of some experiments that explicitly measure electron spin polarization (i.e., with the use of a Mott polarimeter for photoemission studies), this value is usually reported in CISS studies as P = (I_a – I_b) /(I_a + I_b), sometimes denoted as measurement asymmetry, A. Here, I_a and I_b refer to a quantity that can be quantitatively measured with oppositely polarized axial components of electron spin in a laboratory frame. For instance, this analysis can be done by comparing the current measured using a magnetized ferromagnetic electrode out of plane for opposite orientations. In this context, the spin polarization described in experimental reports henceforth refers to the latter definition.

While more systematic investigations are still required to advance our understanding of CISS, there has been significant experimental progress to elucidate the environmental conditions in which spin selectivity can be detected. There has also been a wide variety of experiments probing the CISS effect under different regimes for charge transport, transfer, and transmission. All these efforts have led to questions and challenges in our understanding of the CISS effect. Below, we describe experiments that have contributed insight into mechanistic aspects of the CISS effect and have been the focus of debate. In particular, we focus on results that may have fundamental relevance for exploiting the CISS effect in quantum information technologies, experiments that have taken the next steps toward elucidating the potential biological significance of CISS, and solid-state materials that may serve as robust platforms to explore coherent vs incoherent properties in charge and spin transport.

Spin-Polarized Charge Transport in the Linear vs Nonlinear Regime

Investigations of the CISS effect naturally led to the design and realization of device configurations that incorporate chiral molecules between metal electrodes, which attracted interest for applications in molecular based spintronics. The device potential has been demonstrated in memory structures with low power consumption at room temperatures,^35,36 magnetoelectronic devices with CISS-based spin-valve sandwich structures,^24,37,38 and Hall devices with a two-dimensional (2D) electron-gas system based on self-assembled monolayers (SAMs) of chiral molecules.^29,39 Besides these applications, the CISS devices also provide a platform to examine the fundamental properties of chiral systems in controlled environments. However, the systematic quantitative analysis of device performance and definitive correlations of device functions with CISS properties is challenging in practical device structures. Difficulties arise because measurable signals due to CISS from metal–insulator (molecular film)–metal junctions may be small and convoluted with spurious effects due to shorts or degradation of organic films.

Recently, the CISS transport mechanism has been the focus of a debate over whether CISS can manifest in magnetoconductance (MC) in a chiral molecule junction in linear and/or nonlinear regimes based on the fundamental Onsager relation.^41,42 Specifically, this question is manifested experimentally in whether or not a measurable spin-valve-like effect in two-terminal devices using chiral molecule junctions should be possible due to CISS. Addressing this debate, Liu et al. reported the observation of CISS-induced MC in vertical heterojunctions of (Ga,Mn)As/polyalanines/Au (Figure 2a,b).⁴⁰ With the advantage of a magnetic semiconductor as an electrode, no oxide barrier is needed, as the Schottky contact between Au and (Ga,Mn)As mitigates the shorting problem in all-metal junctions. The perpendicular magnetic anisotropy of the strained (Ga,Mn)As also ensures the optimal detection of electron spin polarization through polyalanines. In this optimized structure, pronounced and robust MC signals enable a rigorous examination of its bias dependence, which shows both linear- and nonlinear-response components (Figure 2c). This realization of CISS in a two-terminal semiconductor device may serve as a precursor for spin injection and detection in semiconductors without using magnetic materials.

Figure 2.

Spin-polarized charge transport in chiral-induced spin selectivity (CISS) devices. (a) Schematic of the device structure of a (Ga,Mn)As/polyalanines/Au vertical junction. (b) Junction conductance vs perpendicular magnetic field measured at a DC bias current of 100 μA. The garnet arrow indicates the direction of the (Ga,Mn)As magnetization, and the gold arrow represents the direction of the electron spin polarization. The black and red dashed arrows indicate the sweeping direction of the magnetic field. (c) ΔG_J as a function of bias current from I–V measurements at different fields (black squares) and MC measurements at different biases (red triangles). Blue line is a linear fit to the black squares. Adapted with permission from ref (40). Copyright 2020 American Chemical Society.

The Role of Spin–Orbit Coupling

Early studies of electron scattering asymmetries began with vapor-phase chiral molecules. Experiments on spin-dependent attenuation of electron beams by Mayer and Kessler found that the presence of a heavy element, such as ytterbium, bound to a chiral molecule in the gas phase could significantly enhance the transmission asymmetry.⁴³ These findings agree qualitatively with earlier theoretical models, indicating that the presence of a heavy atom in a chiral molecular environment should enhance the spin- and chirality-dependent asymmetry in electron-molecule interactions, likely due to increased SOC effects.⁴⁴ These studies were extended using chiral bromocamphor derivatives.⁴⁵ Subsequent experiments found that the degree of spin-polarized electron transmission asymmetry could be modified for nearly identical molecules simply by substituting the coordinating species. Spin-selective electron transmission asymmetry through vapors of chiral camphor derivatives was observed to increase roughly in proportion to the atomic number of the coordinated atom, as Pr (Z = 59) < Eu (Z = 63) ∼ Er (Z = 68) < Yb (Z = 70).⁴⁶ Interestingly, molecules with multiple heavy atoms, such as dibromocamphor, did not exhibit higher asymmetries than their singly brominated counterparts.

To explore the influence of incorporating heavy-metal species in chiral molecular films, Stemer et al. (see Figure 3) used ultraviolet photoelectron spectroscopy (UPS) to characterize magnetization-dependent ionization energies of DNA SAMs formed on ferromagnetic substrates with and without the specific binding of mercury ions at base pair mismatches.⁴⁷ Incorporating 1 equiv of Hg²⁺ in DNA hairpins with only a single helical turn was sufficient for the manifestation of spin-dependent effects at room temperature, while no magnetization-dependent effects are apparent in the samples composed of identical DNA without mercury. At high metal loading, the helical structure of the DNA hairpins was found to invert. This inversion was accompanied by a corresponding reversal in the preferred magnetization orientation for photoionization. Analogous to earlier gas-phase experiments,⁴³ increased incorporation of heavy elements did not further increase spin-dependent interaction asymmetries, indicating that multiple heavy atoms may induce compensating rather than amplifying effects. Recent studies on peptides incorporating paramagnetic species reach similar conclusions with respect to the increase of spin polarization effects.²⁸ These studies highlight the tunability of chiral molecular systems via the incorporation of heavy species, a powerful tool in engineering highly spin asymmetric systems for spintronic and quantum computing applications.

Figure 3.

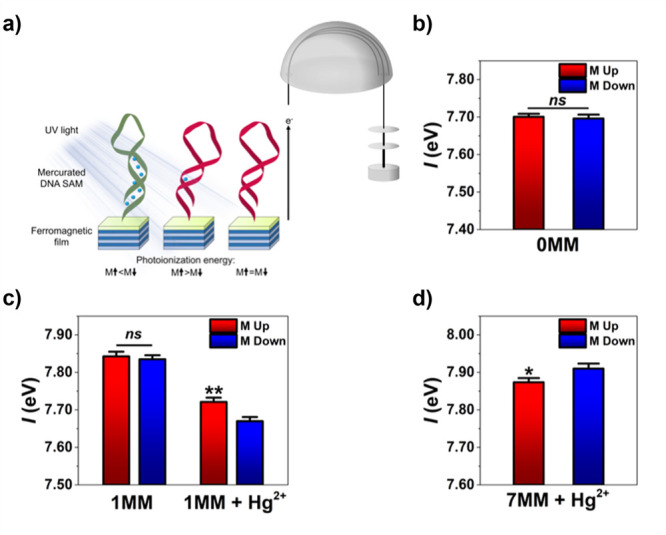
Spin-dependent photoelectron scattering of DNA hairpins. (a) Schematic depicting spin-dependent photoelectron scattering through self-assembled monolayers of DNA hairpins on ferromagnetic films, characterized by ultraviolet photoelectron spectroscopy. Spin-dependent ionization cross sections result in differential charging, physically manifested as substrate magnetization-dependent photoionization energies of the chiral organic films. (b,c) Spin-selective effects were only observed in short (∼1 helical turn) DNA hairpins that contained mercury bound at thymine–thymine mismatches due to enhanced molecular spin-orbit coupling. (d) Spin selectivity was reversed in DNA hairpins containing 7 mismatches and stoichiometric amounts of mercury ions, which was shown to invert the chirality of the helical hairpins. All panels reproduced with permission from ref (47). Copyright 2020 American Chemical Society.

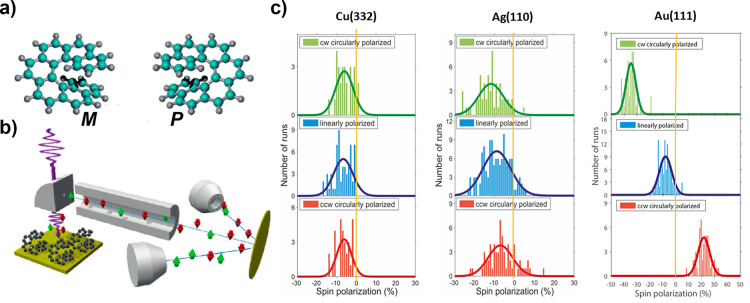
The role of SOC in underlying substrates has also been the focus of investigations. Early CISS experiments were performed predominantly on gold substrates, because the helical biomolecules studied could be readily thiolated on one end to form a strong bond with the substrate. Heavy-metal substrates, such as gold, emit electrons with a preferential spin orientation when excited by circularly polarized light. The spin orientation of the emitted electrons is linked to the helicity of the light. In noble metals, the d-electron SOC constants are measured to be 0.1, 0.25, and 0.72 eV for Cu, Ag, and Au, respectively.⁴⁸ On single-crystal Au(111), circularly polarized ultraviolet radiation just above the work function excites the Λ₄³Λ₅ → Λ₆¹ electronic transition, from the spin-polarized occupied band into an unoccupied plane–wave final band (Λ₆) near the L point of the Brillouin zone. For Cu and Ag, in addition to the lower SOC, the initial state is a Λ₆³ state that produces only weak spin polarization.⁴⁸ Such an excitation with circularly polarized light then yields longitudinally polarized electrons with respect to the quantization axis (i.e., the k vector of the exciting radiation). It is thus important to excite the system at normal incidence and also to extract electrons normal to the surface. For Au(111), spin polarization values up to P = 30% are obtained just above the vacuum level.^20,48 Due to the electronic structure of polycrystalline gold, the spin direction is reversed compared to Au(111), and the magnitude is also significantly smaller. Nevertheless, this substrate dependence suggested that the strong SO interaction in heavy metals extends to the helical adsorbates that consists of light atoms, including C, N, O, and H.⁴⁹

For these three noble metals, Au, Cu, and Ag, systematic CISS experiments were performed for adsorbed monolayers of enantiopure hepta-helicene.⁵⁰ For linearly polarized exciting light that produces unpolarized photoelectrons in the substrate, M-helicene yields a spin polarization of P = −6.7% on Cu(332), P = −9.0% on Ag(110), and P = −8.0% for Au(111) (see Figure 4 center (blue) histograms). Circularly polarized excitation that already produces polarized photoelectrons in Au and, to a limited extent, also in Ag substrates, generates additional spin polarization. This effect is particularly noticeable for Au(111). There, clockwise (cw) circularly polarized light (upper green histograms) yields a total spin polarization of P = −35% for M-[7]-helicene, while counterclockwise (ccw) polarized light (lower red histograms) produces P = −22%. For P-helicene, the sign of the spin polarization switches, and the action of cw- and ccw-polarized light on the total spin polarization is also reversed.⁵⁰

Figure 4.

Spin polarization of photoelectrons from Cu, Ag, and Au substrates transmitted through a monolayer of M hepta-helicene. (a) Structures of enantiomers. (b) Experimental setup for photoemission and Mott analyzer. (c) Green, blue, and red histograms (from top to bottom) represent excitation by clockwise (cw) circularly, linearly, and counterclockwise (ccw) circularly polarized light at λ = 213 nm, and thus emitting electrons slightly above the vacuum level of the systems. Adapted with permission from ref (50). Copyright 2018 American Chemical Society.

Notably, it was also shown that the CISS effect occurs for bacteriorhodopsin adsorbed on aluminum oxide⁵¹ and for DNA bound to Si(111);⁵² both systems lack significant SOC. The influence of the helical organic molecules on CISS, at least in over-the-barrier transmission, thus appears to be independent of the substrate, even though recent theoretical models suggest proximity effects may exist.⁵³ An initial spin orientation may still contribute to reaching high spin polarization. However, it is promising that neither heavy substrate elements nor magnetic substrates are required to generate spin-polarized electrons from helical organic molecules. These results lift possible restrictions in designing spintronic elements and motivate the application of CISS in (electro-)chemistry⁵⁴ and to biological settings.⁵¹

Long-Lived Effects and Magnetic Exchange Interactions

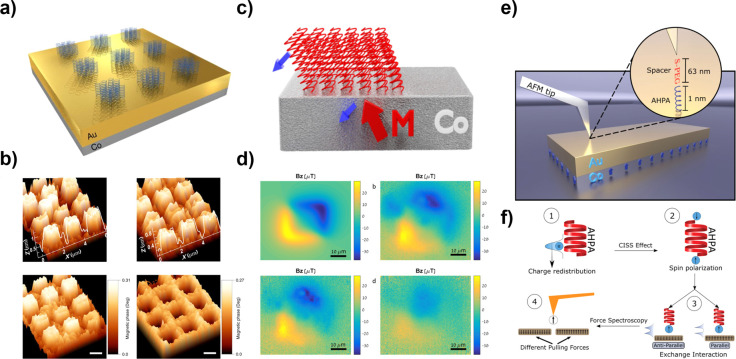
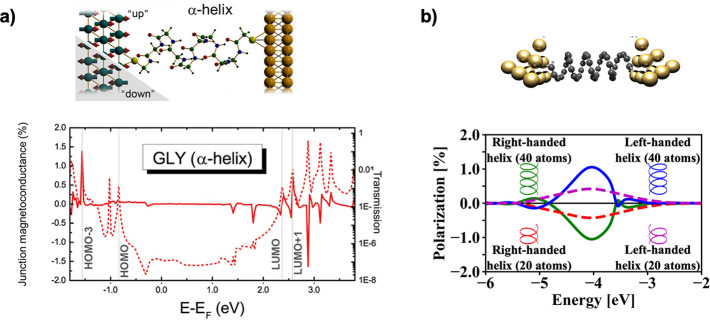
The plethora of experimental configurations that have involved the adsorption of chiral molecular layers on ferromagnetic substrates indicate the importance of possible interactions between molecules, substrates, and interfacial effects.^36,55−58 This molecule–substrate interaction is expected to be spin-sensitive due to short-range magnetic exchange interactions: As chiral molecules approach the surface, charge reorganization and spin polarization should take place, depending on the handedness of the molecules. An early example of this phenomenon was observed in magnetization switching of ferromagnetic thin layers induced solely by the adsorption of chiral molecules without external magnetic fields or spin-polarized currents.³⁶ The effect of adsorbed chiral molecules on the properties of a ferromagnetic substrate was examined by studying the adsorption of l- and d-oligopeptides on thin ferromagnetic films in patterned arrays, with an undefined initial out-of-plane magnetization (Figure 5a,b). Following molecular adsorption, the direction of the magnetization was found to depend on the handedness of the adsorbed chiral molecules. Importantly, fewer than 10¹³ electrons per cm² are sufficient to induce a reversal of the magnetization on the ferromagnetic layer in the direction perpendicular to the surface. We note that the current density required for common mechanisms in modern magnetoresistive random-access memory, such as spin-transfer torque memories, is 10²⁵ electrons per cm². The high efficiency of magnetization is now hypothesized to result from the molecule–substrate exchange interaction. As such, this concept could be used to achieve simple surface spintronic logic devices.

Figure 5.

Chiral-induced spin selectivity effect and ferromagnetic substrates. (a) Experimental scheme and (b) topographic (top) and magnetic phase (bottom) images of chiral α-helical peptides adsorbed on perpendicularly magnetized substrates showing opposite magnetization induced by opposite enantiomers (left- and right-hand columns). Panels (a,b) reproduced with permission under a Creative Commons CC BY license from ref (36). Copyright 2017 Springer Nature. (c) Experimental scheme and (d) magnetization using NV center magnetometry. In (d), the top left image is a simulation of substrate magnetization after 4 h, and experiments show decreasing magnitude after 4 (top right), 8 (bottom left), and 12 (bottom right) h. Panels (c,d) Reproduced with permission from ref (59). Copyright 2021 American Chemical Society. (e) Experiment schematic and (f) measurement mechanism of atomic force microscopy (AFM)-based spin-exchange microscopy using chiral molecules. Panels (e)-(f) reproduced with permission from ref (60). Copyright 2019 John Wiley & Sons.

The surprising results described above led to the important question of whether the magnetization reorientation due to the adsorption of chiral species is transient or persistent. Meirzada et al. recently used nitrogen–vacancy (NV) center magnetometry to monitor this chiral adsorption process and resultant magnetization in thin ferromagnetic films.⁵⁹ The authors report a long time scale magnetization of hours to days, which was correlated with the eventual degradation of chiral film integrity, measured by the tilt angle change of surface-bound molecules (Figure 5c,d). This effect was attributed to coupling a magnetic dipole across the chiral molecule layer and the magnetic substrate, which may be stabilized by a sufficiently large magnetic exchange energy.

Ziv et al. further investigated the roles of magnetic exchange effects using a scanning probe method that relies on nonferromagnetic tips functionalized with chiral molecules (Figure 5e,f).⁶⁰ This approach enabled local magnetic imaging similar to magnetic exchange force microscopy.⁶¹ The authors found that transient spin polarization accompanying charge redistribution due to the CISS effect in the chiral molecules enables spin exchange interactions with magnetized samples, distinguishing domains magnetized up vs down by different forces exerted on atomic force microscopy (AFM) cantilevers near the sample surfaces.⁶⁰ The forces were hypothesized to result from either symmetric or antisymmetric spin alignment in the wave function overlap between molecules on the tips and the magnetized sample. Similarly, recent Kelvin-probe force microscopy measurements by Ghosh et al. on ferromagnetic films coated with chiral SAMs revealed electron spin-dependent charge penetration across the molecular interface.⁶² This dependence of wave function overlap between magnetized materials and chiral molecules on the spin-exchange interaction could also be used to rationalize the spin-selective contributions to stereoselective interactions between chiral molecules that result from induced dipole–dipole interactions.²⁹

Importantly, it was shown that the magnetic exchange interaction described above could be exploited to separate enantiomers by merely adsorbing them on a ferromagnetic substrate that has a magnetization perpendicular to the surface.⁵⁷ The mechanism for chiral molecules to induce a magnetization that can lead to this enantioseparation is shown in Figure 6. These results are particularly exciting due to the critical importance of highly efficient and generalizable approaches to enantiomeric separations of pharmaceuticals and agrochemicals. Unambiguous enantioselectivity on a ferromagnetic substrate was obtained for a variety of chiral molecules and magnetic substrates. That is, while one enantiomer adsorbs more rapidly than the other when the magnetic dipole is pointing up, the other adsorbs faster when the substrate is magnetized in the opposite direction. The interactions between the chiral molecules and the magnetized substrate are not affected by the magnetic field but by the interaction between the spin-polarized electrons in the molecule and the spin of the electrons on the substrate. A recent study by Lu et al. suggests that this enantiospecificity in adsorption is likely dominated by kinetic rather than thermodynamic control, with extreme sensitivity to solution conditions, molecule ionization state, and binding geometry of the adsorbing species.⁶³ Elucidating the importance of these and other environmental parameters will be crucial for generalizing this separation procedures for left- and right-handed species. Further, how these proximity and interfacial effects are dictated by molecular chirality could be extended to quantum technologies that have only begun to be explored, such as their use in controling superconducing interfaces (see below).

Figure 6.

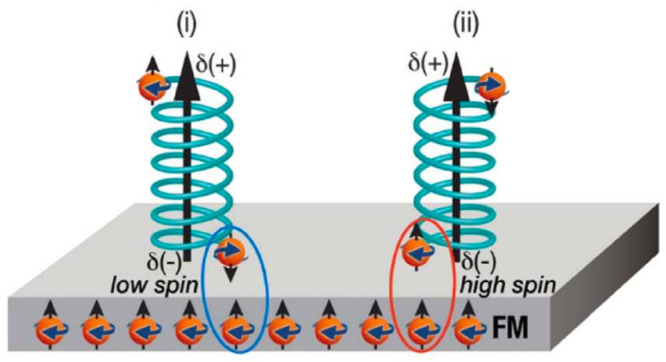
Interactions between chiral molecules and ferromagnetic (FM) surfaces. As a chiral molecule approaches the FM substrate, its charge polarization generates a spin polarization at the two ends of the molecule. For a specific enantiomer, the interaction between the magnetized surface and the molecule (circled in blue and red) follows a low-spin or a high-spin potential, depending on the direction of magnetization of the substrate. Reproduced with permission from ref (57). Copyright 2018 American Association for the Advancement of Science.

Temperature Dependence

The room-temperature spin-selectivity in electron propagation through chiral molecules initially garnered significant attention for potential chiral organic alternatives to solid-state magnetic materials for room-temperature spintronics applications.¹⁰ Not surprisingly, experimental observations using biologically relevant oligonucleotides, proteins, peptides, and amino acids to filter or to polarize electron spins under ambient conditions have also led to questions about biological relevance and whether these systems may exploit CISS under physiological conditions. Now, with a focus on developing quantum device architectures that could operate above cryogenic temperatures, these room-temperature spin-dependent interactions offer significant advantages of chiral molecules to control spin and charge states for logic, sensing, and storage.

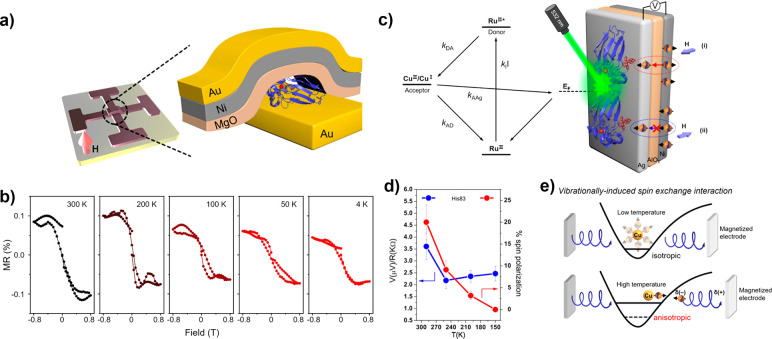
Temperature dependencies of the CISS effect have been difficult to extract in some proteins due to the concomitant influence of temperature on charge transfer. In other cases, CISS spin-valve-like devices displayed either weak to no temperature dependence on spin-dependent transport^24,37,65 or decreases in magnetoresistance with decreasing temperature.³⁸ These observations contrast with traditional devices using solid-state magnetic materials that exhibit giant magnetoresistance and show, conversely, an increasing magnetoresistance with decreasing temperature. The direct relationship between magnetoresistance and temperature in CISS devices may be linked to conformational changes in the secondary and/or tertiary structures of molecules that were used as spin-filtering components in these device architectures.³⁹ Structural changes could therefore change possible electron tunneling pathways as a function of temperature. As an alternative explanation, Sang et al. recently showed that vibronically activated electronic exchange interactions in the ruthenium-labeled blue copper protein azurin are responsible for the enhancement in spin selectivity at elevated temperatures (Figure 7).⁶⁴ Measuring temperature-dependent spin polarization in Ru-azurins offers the advantage that the underlying charge-transfer kinetics depends only weakly on temperature, enabling deconvolution of spin-selective effects. The experimental observations that the strength of the CISS effect increases with increasing temperature, coinciding with increasing vibrational excitations, have led to the possible mechanistic role of vibrationally assisted SOC in promoting spin-dependent dissipation.⁶⁶ Further theoretical insights on these effects are described below.

Figure 7.

Temperature dependence of spin-dependent electron transport through the protein azurin. (a) Schematic of magnetoconductance device with wild-type azurin sandwiched between ferromagnetic and normal metal electrodes. (b) Magnetoresistance measured from 300 to 4 K. (c) Measurement scheme to detect photoinduced charge transfer between a ruthenium donor and copper acceptor groups and a ferromagnetic substrate. (d) Spin-independent photovoltage and spin polarization percentage as a function of temperature. (e) Model of vibronically activated spin-polarization. Adapted with permission from ref (64). Copyright 2021 American Chemical Society.

Possible Biological Implications

Structure–function relationships are critically important in biological protein systems. The activity of a specific receptor may be significantly modulated by the binding of a molecule elsewhere on the protein, even if this binding interaction occurs far away from the receptor site, in a process known as allostery. Generally, the allosteric effect describes conformational changes which take place upon the binding of a (usually small) molecule, which subsequently induce local changes in receptor activity. However, recent work is challenging this general description. Banerjee-Ghosh et al. recently reported that charge redistribution within proteins may influence binding activity in a protein without causing significant conformational changes to the system (Figure 8).⁶⁷ The authors investigated this charge-redistribution allostery by studying the binding behavior of an antigen to a metal-surface-tethered antibody, which was capable of binding to a polyhistidine moiety on the antigen. The interactions between the two species were characterized as a function of interaction time via fluorescence spectroscopy. As the antigen, which has a strong dipole moment, approaches the tethered antibody, it induces charge redistribution within the antibody. Since the antibody is itself chiral, the charge redistribution was accompanied by spin polarization, as electrons with one spin experience lower barriers to migration across the molecule compared to those of the opposite spin.²⁹ The antibody was tethered with a linker molecule to a magnetic substrate which was either magnetized parallel or antiparallel to the surface normal. Charge injection from the chiral antibody into the magnetic substrate, or vice versa, was thus determined by matching between the spin orientation of the electrons in the substrate magnetic subbands and the handedness of the antibody.

Figure 8.

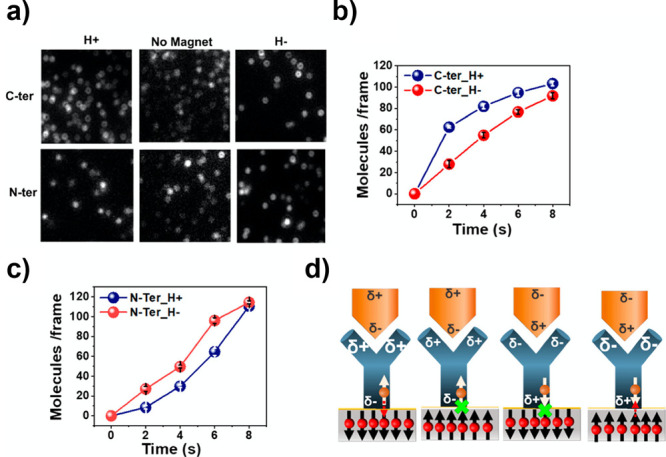
Evidence for allosteric long-range charge reorganization in proteins. (a) Fluorescence microscopy images of antibody–antigen binding to oppositely magnetized substrates. (b,c) Reaction kinetics of the binding interaction. (d) Schematic of the spin-valve-like behavior gating charge reorganization when antibodies are adsorbed on ferromagnetic substrates. Reproduced with permission from ref (67). Copyright 2020 by American Chemical Society.

When the substrate was magnetized, such that the polarized electrons at the metal–molecule interface were more easily transferred, then the overall charge reorganization induced in the antibody by the approaching antigen was greater than when charge transfer between the antibody and magnetic substrate was suppressed. In this sense, the CISS effect was used as a current valve to modulate charge redistribution in the antibody. By monitoring the fluorescence of the adsorbed antigens with time, Banerjee-Ghosh et al. reported a difference in the rate of adsorption as a function of the substrate magnetization orientation, presumably as a consequence of increased or suppressed charge reorganization allostery. A similar effect was reported for the same antibody linked to a nonmagnetic gold substrate via a chiral cysteine linker, in which case the binding kinetics were controlled by the matching between the linker and antibody chirality. The modulation of binding activity appeared to be unaffected by the sign of the spin polarization at either end of the antibody, but was determined rather by the relative degree of charge redistribution, which was facilitated in this case by the CISS effect.

Ghosh et al. further reported that the degree of binding modulation may be tuned through control of the dipole moment across the binding antigen.⁶⁸ The unmodified antigen used in the experiments described thus far binds to the surface-tethered antibody at its positively charged C-terminus. However, upon binding a negatively charged substrate molecule, the dipole moment across the antigen was found to decrease, thus reducing the induced charge redistribution across the antibody. The magnitude of the charge-reorganization allostery was observed to decrease along with the decreasing molecular dipole (across the longitudinal axis) of the antigen, measured as the percent difference in fluorescence microscopy signal for antigen binding to antibodies tethered to magnetic substrates with magnetization axis parallel vs antiparallel to the surface normal. The total rate of binding was also observed to decrease, regardless of the magnetization orientation of the substrate, upon reducing the magnitude of the dipole of the antigen.

Although the CISS effect was incidental to the work described above, a potential link between charge reorganization and biochemical activity is suggested. Kumar et al. previously found the correlation of spin polarization with charge reorganization in chiral molecules by studying SAMs of chiral oligopeptides tethered to the surface of modified Hall effect devices.²⁹ Building upon this finding, the authors calculated the interaction energy for closed-shell chiral small molecules of the same handedness vs of the opposite handedness and found that, even in the absence of steric considerations, the spin polarization accompanying the charge reorganization induced by proximity between the molecules was sufficient to substantially affect of the calculated interaction energy. For two molecules of opposite handedness, the spin polarization accompanying the charge reorganization induced by molecular proximity will result in the spins of the electrons at the molecular interaction termini being parallel. If the molecules are of opposite handedness, the spins will be antiparallel. As a consequence of exchange interactions between the electrons at the interaction termini, the interaction energy in these two situations is significantly different. In light of the charge-reorganization allostery proposed by Banerjee-Ghosh et al., one can begin to see how the CISS effect might become significant in biochemical contexts. The activity of certain proteins appears to be sensitive to changes in the charge distribution across the molecule, even if those changes are initiated at points far from a specific receptor site. The degree of interaction between chiral species depends on both steric considerations as well as exchange interactions and is thus sensitive to the chirality matching between species. Two molecules of matching chirality will experience a lower interaction energy, enabling the species to come into closer contact and thereby inducing a larger degree of charge reorganization, which may then affect the biochemical activity of the interacting molecules. Such a cascade of effects may link the CISS effect to larger-scale modulations of biochemical activity. However, it is important to keep in mind that the experiments highlighted so far all involve surface-tethered molecules, and more work will be required to determine whether the magnitude of these interactions is significant in technologically relevant devices and in biologically relevant contexts.

Driving Enantioselective Chemical Reactions

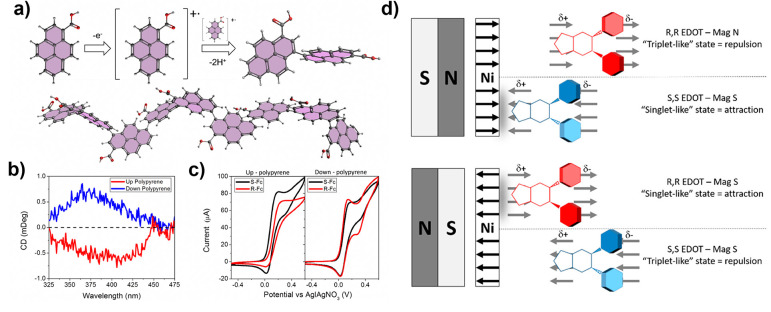
It was found recently that spin selectivity can control both electrochemical reduction and oxidation.⁶⁹ More generally, it appears that electron spin helicity can be used to direct enantioselectivity in chemical reactions. As an example of an oxidation process, electropolymerization of 1-pyrenecarboxylic acid was performed on a magnetic electrode (10 nm of Ni and 10 nm of Au on ITO) that was magnetized “up” or “down” relative to the electrode surface. Figure 9a shows a reaction scheme for the formation of polypyrene. Initiation of the reaction involves electro-oxidation of the monomer unit to form a radical cation. The steric constraints of the pyrene rings lead to a propeller-like arrangement of the monomers; control over their stereo arrangement imparts axial chirality to the polymer chain. Figure 9b shows the circular dichroism (CD) spectra of the pyrene polymer films on the electrode surface. In turn, the red curve shows the CD spectrum with the electrode magnetized in the “up” direction and the blue curve corresponds to the case for magnetization in the “down” direction. The red and blue curves exhibit opposite Cotton effects in pyrene’s excimer spectral region.

Figure 9.

Reaction scheme and chirality in electropolymerization. (a) Reaction scheme for the polymerization of 1-pyrenecarboxylic acids into polypyrene which exhibits a helical twist (see main text for more details). (b) Circular dichroism (CD) spectra for electrodes coated with polypyrene where a magnetic field was applied up (red) or down (blue) during electropolymerization. (c) Electrochemistry measurements on (S)- (black) or (R)-ferrocene (red) with the up (left) or down (right) polypyrene-coated working electrodes. Panels (a–c) reproduced with permission from ref (69). Copyright 2020 John Wiley and Sons. (d) Interaction scheme between a ferromagnetic electrode and chiral monomers. Panel (d) reproduced with permission from ref (70). Copyright 2020 American Chemical Society.

The chirality of the polymer-coated electrode was confirmed by performing cyclic voltammetry with a chiral ferrocene (Fc) redox couple. Figure 9c shows voltammetry data collected using the polypyrene-coated films as working electrodes for two different enantiomerically pure solutions of chiral ferrocene: (S)-Fc (black) and (R)-Fc (red). The voltammetric peak currents indicate that the “up” grown electrode is more sensitive to (S)-Fc, while the “down” grown electrode is more sensitive to (R)-Fc. Similar dependencies for redox properties with chiral working electrodes were reported elsewhere and further corroborate the chirality demonstrated in the CD measurements.⁷¹ These results indicate how chiral spin transport can lead to highly amplified downstream chemical products.

Tassinari et al. went on to show that electropolymerization of R,R- and S,S-ethylenedioxy-thiophene monomers on a ferromagnetic electrodes depends on substrate magnetization, and thus electron spin orientation.⁷⁰ The enantioselectivity afforded by this magnetic field control was attributed to different reaction rates of the electron-transfer step and of chiral monomer binding to the electrode surface depending on favorable (spins aligned in a singlet like orientation) vs unfavorable spins (spins aligned in a triplet like orientation) interaction (Figure 9d). Thus, the magnetic exchange interaction between chiral species and ferromagnetic surfaces could be used as a driving force in surface chemical reactions.⁷²

Beyond Molecules: Chiral Crystals

In addition to organic chiral molecules, CISS has been discovered recently and studied in crystalline chiral materials. Hybrid organic–inorganic perovskites (HOIP) with large SOC are promising for opto-spintronics applications. In chiral HOIPs, Lu et al. reported conduction asymmetries of up to 86% (measured as percent differences in current at 2 V for “tip-up” and “tip-down” magnetization conditions) in solution-processed 50 nm thin films of chiral lead–iodide hybrid perovskites, as shown in Figure 10.⁷³ Similar values of spin-selectivity were reported recently in conductive atomic force microscopy (c-AFM) measurements of conduction through supramolecular chiral nanofibers assembled on Ni thin films capped with gold.⁷⁴ By tuning the chirality (R- or S-) of the organic methylbenzylammonium constituent, Lu and colleagues showed control over the handedness of the perovskite films studied. More recent reports focused on similar tin–iodide perovskites yielded even higher spin-selectivity values,⁷⁵ nearing 94%, and underscoring the utility of conductive probe microscopy as a powerful tool for rapid and direct characterization of electronic phenomena in chiral materials, particularly as the materials grow in relevance to the broader spintronics community.

Figure 10.

(a) Experimental scheme for magnetic conducting atomic force microscopy measurement of chiral perovskite thin films. (b–d) Current–voltage traces collected for thin films of lead–iodide perovskites containing chiral R-methylbenzylammonium (R-MBA), achiral phenylethylamine, and chiral S-methylbenzylammonium (S-MBA), respectively, as a function of tip-magnetization orientation. Reproduced with permission under a Creative Commons Attribution-NonCommercial License from ref (73). Copyright 2019 American Association for the Advancement of Science.

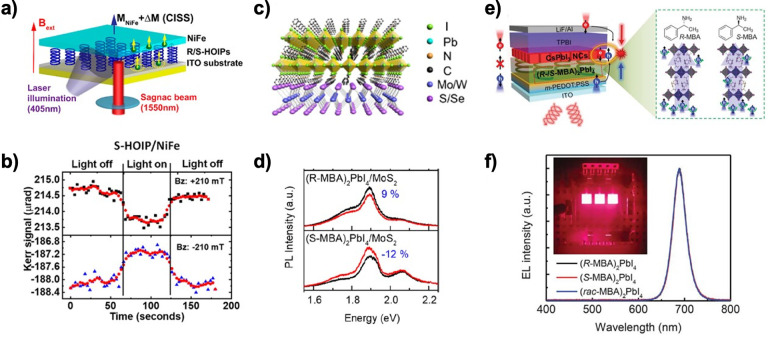
Huang et al. performed Kerr effect measurements on 2D chiral HOIP/NiFe heterostructures using a Sagnac interferometer (Figure 11a) and found that the Kerr signal changes upon illumination (Figure 11b).⁷⁶ Chen et al. realized spin injection in chiral 2D perovskite/monolayer transition metal dichalcogenides (TMDs) heterostructures (Figure 11c,d).⁷⁷ An average spin injection efficiency of 78% was measured in monolayer MoS₂ (WSe₂) from chiral 2D perovskites. Lu et al. studied spin-dependent charge transport in 1D chiral hybrid lead-bromide perovskite, which showed superior stability in comparison to 2D chiral perovskites.⁷⁸ Chiral metal-halide perovskites have further been demonstrated to show spin-LED effects without magnetic fields or ferromagnetic materials by Kim et al. This study achieved 2.6% circularly polarized electroluminescence at room temperature (Figure 11e,f).⁷⁹

Figure 11.

(a) Schematics of the Sagnac magneto-optic Kerr effect experiment at the interface of a chiral-hybrid organic–inorganic perovskite (HOIP) and NiFe substrate.⁷⁶ (b) The change in Kerr signals with photoexcitation under positive and negative out-of-plane magnetic field.⁷⁶ (c) Schematics of the chiral 2D perovskite/transition metal dichalcogenide heterostructure.⁷⁷ (d) Polarization-resolved photoluminescence spectra of the heterostructure excited by a linearly polarized laser of 532 nm.⁷⁷ (e) Schematics of a chiral-induced spin selectivity (CISS) spin-light-emitting diode. (f) Electroluminescence spectrum with CISS layer/CsPbI₃ heterostructures and a device image as inset.⁷⁹ Panels (a,b) reproduced with permission from ref (76). Copyright 2020 American Chemical Society. Panels (c,d) reproduced with permission from ref (77). Copyright 2020 American Chemical Society. Panels (e,f) reproduced with permission from ref (79). Copyright 2021 American Association for the Advancement of Science.

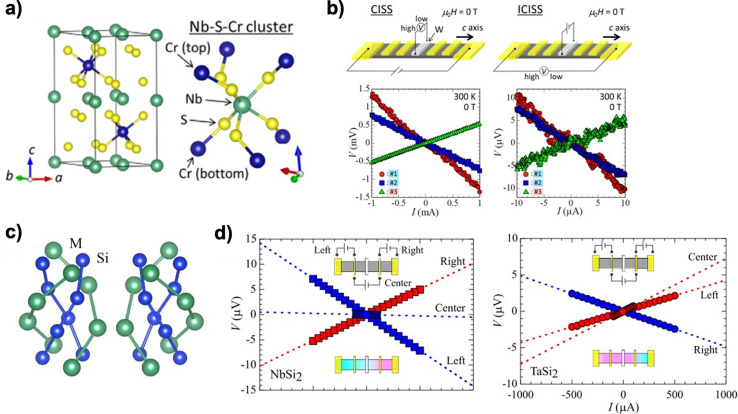
In addition to the hybrid perovskites, CISS has also been investigated in a monoaxial chiral dichalcogenide, CrNb₃S₆, with the current-induced spin polarization along the chiral axis detected by inverse spin Hall effect (Figure 12a,b).⁸⁰ Long distance spin polarization was measured in the chiral disilicide crystals NbSi₂ and TaSi₂ (Figure 12c,d).⁸¹

Figure 12.

(a) Schematics of crystal structures of CrNb₃S₆.⁸⁰ (b) Schematics and electrical measurements of chiral-induced spin selectivity (CISS) and inverse CISS signals.⁸⁰ Panels (a,b) reproduced with permission from ref (80). Copyright 2020 American Physical Society. (c) Schematics of crystal structures of a disilicide compound MSi₂ (M: transition metal).⁸¹ (d) Location variations of the CISS signals of NbSi₂ and TaSi₂.⁸¹ Panels (c,d) reproduced with permission from ref (81). Copyright 2021 American Physical Society.

Finally, as recent work on enantioselective and spin-selective effects in chemistry has begun to include studies on crystalline materials, connections may start to be drawn to topological quantum matter as well.^2,82 Detailed descriptions of the intersections between topology and chirality in crystalline materials have been the focus of recent reviews^83,84 and are beyond the scope of this review. However, we note that emerging properties that lead to the protection of momentum-locked spin states and chiral surface states in topologically nontrivial crystalline materials could intersect with the developing understanding of the CISS effect in molecular systems. Thus, chiral crystalline materials are an excellent platform to explore emerging quantum properties and the viability of using chiral couplings to control quantum information. Further, topologically protected chiral spin textures in magnetic materials such as skyrmions or antiskyrmions that are stabilized by the Dzyaloshinskii–Moriya interaction, which are promising for spintronics devices, also provide a fascinating testbed for quantum computing applications.⁸⁵⁻⁸⁸ Psaroudaki and Panagopoulos recently proposed that these nanoscale magnetization textures themselves could act as quantum bits by quantizing the helicity degree of freedom, albeit at millikelvin temperatures.⁸⁹ By leveraging the CISS effect at magnetic interfaces, an exciting forward-looking direction could be to test the influence of chiral molecule functionalization on the formation, propagation, annihilation, or inversion of these chiral spin textures in ultrathin magnetic films.

Theoretical Insights

Understanding the physical basis of CISS continues to be a challenge.¹³ Nevertheless, reduced models for the spin-polarization mechanism have been used to study distinct physical scenarios for embodiments of the CISS effect. These reduced models involve a variety of approaches employing, for instance, empirical or tight-binding Hamiltonians, and can explore complexity in a systematic manner as described below.

The vast majority of theoretical CISS-related studies rely on model Hamiltonians. Conventional atomic resolution electronic structure methods, such as density functional theory (DFT), have only been applied in a few cases.^14,53,90,91 The DFT-based spin-dependent transport calculations, with the Landauer approach and including SOC, demonstrate the influence of helical structure on spin polarization^14,90 and they correctly describe the increase of spin polarization with molecular length as observed experimentally.^18,91 However, the spin polarizations obtained using DFT are much smaller than the measured values, suggesting that the theoretical description may be missing some key ingredients.

While past experience with DFT for spin-polarized molecules suggests caution,⁹² these results point to intermolecular interactions and interfaces being important for the first-principles description of CISS. Likewise, the roles of interfaces (possibly combined with the collective properties of molecular assemblies) for magnetic signatures in electron transport were explored experimentally.⁹³⁻⁹⁵ In addition, going from a focus on a spin-polarizing helix to a full circuit analysis has been suggested.⁹⁶ Beyond the description of exchange/electronic interactions, intermolecular and interface effects, it may be important to consider nuclear dynamics as well as electronic dynamics.^97,98

As a complement to efforts that aim to establish a comprehensive first-principles theory of CISS, chemical concepts extracted from first-principles calculations on helical molecules, such as electron transport pathways^99,100 and imaginary components of the Hamiltonian,⁵³ may provide steps toward understanding structure–property relationships in CISS. However, in spite of the attractive features of CISS theories within a first-principles framework, first-principles calculations on complex helical structures and assemblies can be challenging.^53,90 Most standard implementations of DFT can treat periodic and/or finite molecular systems, with hundreds or even thousands of atoms in the simulation cell. The computational time for ground-state calculations using local or semilocal exchange–correlation functionals scales with the cube of the number of atoms, while those employing Hartree–Fock or hybrid exchange scale with the fourth power. In view of these difficulties, two main approaches are likely to emerge as powerful tools for DFT analysis of the CISS effect in complex structures: (1) systematic first-principles methods that treat the helical symmetry more exactly^101−103 (and therefore employ only a minimal unit cell to represent the system being studied), and (2) efficient methods for computing exchange interactions^104,105 within such a symmetry-adapted framework.

The development of first-principles descriptions of molecular properties profits from quantitative benchmark experiments.¹⁰⁶ As is often the case in molecular electronics and spintronics, the lack of detailed atomistic control makes it extremely challenging to come up with such quantitative benchmark experiments for CISS. Therefore, it is critical to have access to systematic experimental studies that probe the dependence of spin polarization on molecular structures and their arrangements, as recently provided in ref (18). Together with further related studies, for example, on the role of local vs axial chirality or on subtle structural modifications via chemical substituents or heteroatoms, benchmark experiments could provide a foundation on which to develop a first-principles theory of CISS. While efforts in this area have made tremendous progress, the effect is still underestimated by several orders of magnitude. Thus, first-principles descriptions of CISS might profit from developments in the areas of analytic and tight-binding theories.

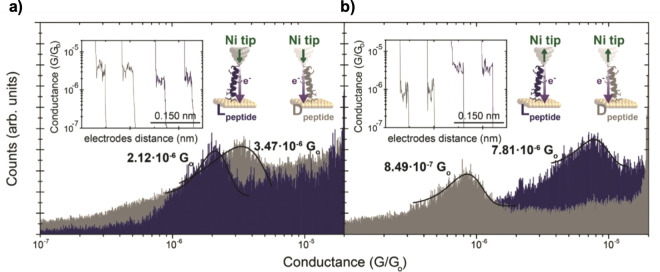
Efforts to explain the CISS effect observed in single peptide molecules with well-defined chirality (l- and d-peptides) were recently put forward, as shown in Figure 13. The transport model was based on the Landauer regime and used a Green’s function technique. In the presence of spin polarization, the conductance is spin dependent and the transmission contains information associated with the molecular chirality, helicity, and the spin propagation direction. This theoretical model explained four possible scenarios of the observed current asymmetries in single chiral molecular junctions sandwiched between a polarized Ni tip and Au electrodes.¹⁰⁷ These four different scenarios with different conductances indicate that spin rectification applications close to the zero-bias limit might be possible.

Figure 13.

(a) For a realistic peptide helix, a density functional theory-based Landauer approach including spin-orbit coupling (SOC) yields spin polarization as rather narrow peaks far from the Fermi energy (solid line in the plot, reported as junction magnetoresistance; using Perdew-Burke-Ernzerhof, PBE, functionals).⁹⁰ (b) For a model helix of equidistant carbon atoms (capped by two hydrogens at each end), spin polarization over a broad energy range close to the Fermi energy is obtained, but it can be traced back to spin-orbit transfer from the gold electrodes rather than resulting from SO intrinsic to the helix (in the plot, the Fermi energy is between −5 eV and −4 eV for gold; using a B3LYP functional).⁵³ Note that the exchange–correlation functional PBE (plot in (a)) features 0% Hartree–Fock exchange, while B3LYP (used on the right) has 20%, and that the absolute values of spin polarization depend on this exchange admixture. Importantly, the polarization changes sign when the helicity is inverted and increases with molecular length (plot in (b)). Panel (a) reproduced with permission from ref (90). Copyright 2018 American Chemical society. Panel (b) reproduced with permission from ref (53). Copyright 2020 American Chemical Society.

Using the Dirac Hamiltonian for a free electron, it was predicted that in the nonrelativistic limit, a spin-dependent energy shift for electrons with momentum along the axis of a weak magnetic field arises which is orders of magnitude larger than the quantum mechanical Zeeman shift.¹⁰⁸ This could be the source of the experimental gap in the computed spin polarization found in current CISS theories. In the low-mass approximation for free electrons (where chirality coincides with helicity), the author derives a symmetry for such a system that is evocative of spin- to orbital-angular momentum conversion demonstrated in vortex beams, but instead for energy to chirality conversion. This effect appears to arise from fundamental magnetic symmetries of free electrons under the influence of static fields, and such mutually correlated changes in energy and chirality can be directly measured in nano-, meso-, and macro-scale systems. A simple example of this sensitive dependence has been demonstrated in the chirality of nascent crystals and low-energy fluctuations introduced by perturbing the crystallization solution.¹⁰⁹

In the following sections, theoretical insight into physical contributions to the CISS effect are addressed using some of the above-described approaches. These include broken symmetries (both space inversion and time-reversal), molecular SOC, intermolecular interactions, electric dipole effects, substrate contributions, vibrational dependencies, and the role of coherence, among others. The unifying mechanism for CISS that accounts for the relative influence of all of these molecular and environmental parameters has not yet been conclusively identified. However, we highlight below recent theoretical studies that have identified each of these possible contributions to account for many of the aforementioned experimental results.

Symmetry Breaking Effects and Reciprocity

The CISS effect requires the absence of spatial inversion symmetry. The sign of the chirality further dictates the sign of the CISS-induced preference of spin currents through a chiral molecule, which also depends on the direction of the charge current. Another requirement is the breaking of time-reversal symmetry. The SOI, which has been found to be critical for CISS and is described in more detail below, does not break time-reversal symmetry, and thus cannot alone (in combination with lack of inversion symmetry) account for the CISS mechanism. In solving the spin-dependent scattering problem for a simple two-path interferometer (i.e., a spin filter), unitary and time-reversal symmetry lead to Kramers-type degenerate transmission eigenvalues.¹¹⁰ In other words, when a helix representing a chiral molecule spans two one-dimensional (1D) single-mode leads, spin polarization of transmitted electrons should not be observed due to time-reversal symmetry. However, time-reversal symmetry can be broken, leading to preferential spin direction in a chiral molecular system (i.e., corresponding to one of the helicity eigenstates of the Hamiltonian) in the presence of bias,^106,111,112 application of a magnetic field (common in nearly all experiments), by assuming leakage of electrons to the environment,¹¹³ by Buttiker probes,^97,114 or by the preselection of angular momentum of injected electrons.¹¹² These fundamental symmetries are imperative to consider in many experimental configurations used to study the CISS effect. Yang et al. showed that two-terminal MC can arise in the nonlinear regime from the breaking of Onsager reciprocity⁹⁶ and even appear in the linear response regime by changing the strength or orientation of the magnetization or a magnetic field.¹¹⁵ These and other recent theoretical studies provide important insights and potentially useful guidelines for detecting magnetoresistance in CISS-based spintronics devices.

Molecular Spin–Orbit Interactions

The SOC that provides a source of magnetic fields for electrons in atoms is a relativistic effect and is thus weak, on the order of a few meV, for the light-atom chiral molecules studied so far. However, it is sufficiently strong to generate a sizable spin polarization through cumulative interactions with the chiral environment. For example, for transport through a large molecule, an electron will encounter and transit many atoms. At each encounter, the SO interaction depends on the orbital orientation and will lead to some weak spin polarization. For a chiral molecule such as DNA, the electron spin polarization is cumulatively enhanced by the preferred orbital orientations of the many surrounding atoms as the electron travels through the molecule, leading to the CISS effect.¹⁹

Theoretical approaches to CISS began with attempts to explain experiments of chiral molecules in the gas phase.^44,116 The theory recognized spin polarization as a single-molecule effect, where the spin-active coupling is the SOC between the scattered electron and the nuclear potential.⁴⁴ The theory was based on symmetry considerations and geometry of the target-molecule system and agreed well with experiments,⁴³ but the effect was small: The polarization asymmetry was only ∼10^–4. It was then a tantalizing surprise when Ray et al.¹⁹ reported a much larger effect in chiral SAMs of amino acids. Minimal models using the Born series were proposed to explain this much larger effect.¹¹⁷ A model of double scattering of single molecules, hypothesizing SOC arising from C, N, and O atoms, produced chirality-dependent spin polarizations of a few percent. One of the most striking predictions of the theory was the existence of energy windows for optimal action of the SOC,¹¹⁸ which was later corroborated experimentally and theoretically by Rosenberg et al.¹¹⁹ More sensitive experiments on DNA SAMs showed extraordinary electron polarizations, so the theory underestimated the CISS effect by a factor of 10.²⁰ No further improvements of the theory in this regime have been realized.

Further experimental progress accessed single-molecule measurements,²³ and simple tight-binding models were proposed,^114,120 assuming sustained quantum coherence and large SOC as an adjustable parameter to fit the large polarizations reported experimentally. A further step included the geometry of the orbitals and the atomic source for the SOC,¹¹¹ using an analytical Slater–Koster approach that identified the transport SOC as a first-order effect in the helical geometry. Such spin coupling goes to zero in nonchiral geometries and obeys time-reversal symmetry with eigenfunctions coming in Kramer pairs.¹²¹ An important ingredient of the minimal model was to include the problem of the electron-bearing orbital filling in determining the energy dispersion of the model.

The SOC is apparently the spin-active ingredient¹¹⁸ for the molecular length dependence of the spin polarization processes. Minimal models place the strength of this coupling and its atomic origins in the range of 1–10 meV,¹¹¹ and the effect may be modulated by orbital overlap effects^111,122 and by hydrogen bonding (as an additional source of electric field, scaling-up the effective SOC, especially for biological molecules such as DNA and polypeptides).¹²³

Intermolecular Interactions

The importance of a chiral molecule’s immediate environment and intermolecular interactions on the CISS effect is clearly evidenced by comparing gas-phase studies with results from high-density films. As described above, spin selectivity could only be unambiguously assigned in gas-phase measurements using chiral molecule derivatives containing heavy atoms with large SOC strengths, which amplified scattering asymmetries.⁴⁶ Subsequent results revealed spin-selective transmission of electrons through oriented self-assembled films of chiral molecules, with photoelectron spin polarization in subsequent studies exceeding 60% for DNA assemblies.^19,20 The environment can play a role by changing molecular structural characteristics and dynamics, and due to delocalization of an electron’s wave function over more than one molecule during charge transport and scattering through a film. Specifically, intermolecular and environmental conditions are expected to influence: (1) dissipation, decoherence, and structural disorder of the system, (2) electron leakage to the environment, and (3) spin polarization mechanisms in different transport regimes (i.e., tunneling vs hopping) to different extents. Direct biological implications of these intermolecular interactions could manifest in enantioselective biorecognition and in charge transport across a membrane or through a protein.

The number of theoretical studies that have taken molecular film density into account to rationalize experimental results is limited. One of the earliest theoretical investigations by Medina et al. suggested that increasing electron wave function overlap with deeply penetrating orbitals in high-density films vs electron scattering through vapor-phase chiral molecules could account for enhanced SOIs.¹²⁴ More recently, an interesting and surprising finding was that formally closed-shell peptide helices can be readily spin-polarized in equilibrium when brought together in an organized fashion,¹⁴ as opposed to isolated helices. Intermolecular interactions in organized and dense arrays of chiral molecules were shown to be crucial for obtaining a broken spin symmetry (i.e., a singlet) state, which was not observed in modeling analogous arrays of linear molecules. Building on this work, when considering geometries for quantum device architectures that exploit chiral chemical modification and approach the single-molecule and qubit limit, it will be important to understand how necessary intermolecular interactions are for device miniaturization.

Aside from their relevance to spin transport physics or Heisenberg-type spin–spin interactions with magnetic substrates, symmetry-based helicity-dependent effects may also lead to reconsideration of standard descriptions of induction and dispersion forces between chiral molecules. In analogy to CD, both electric dipole and magnetic dipole transition elements are required to describe these forces, allowing for chirality-sensitive forces^125,126 with potentially significant consequences in, for example, the study of intermolecular interactions in biology. These considerations are summarized schematically in Figure 14.

Figure 14.

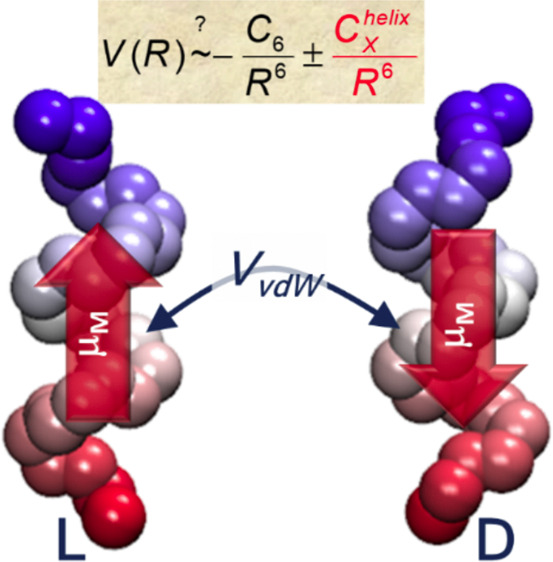
In the case of chiral molecules, induction, and dispersion forces encoding electric dipole–dipole interactions require additional modifications to account for exchange-mediated interactions related to the chiral-induced spin selectivity effect.

Dipolar Effects

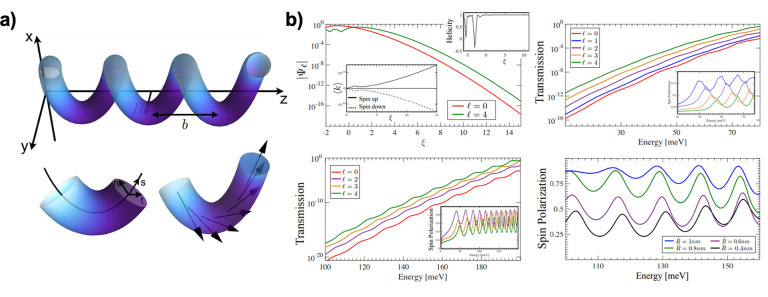
Michaeli and Naaman showed that the chiral molecular geometry induces correlations between the electron spins and their flow direction and that this accounts for the spin selectivity of the molecules (Figure 15).¹²⁷ Moreover, by adding an overall dipole potential along the molecule, it is possible to enhance electron transport. After computing the electronic states of the molecule, one can calculate the local helicity by calculating the local velocity of each spin. The results indicate that, for a right-handed helix, the local helicity of the spin up (down) electron is always positive (negative) in the tail of the wave function. Therefore, the spin selectivity effect takes place.

Figure 15.

(a) The helical tube. Electrons are confined to a helical tube of radius R and pitch b, s is the position along the helix tube, and vectors n and t span the plane perpendicular to s. A term in the Hamiltonian acts as an effective Zeeman field rotating as a function of the position along the helix. (b) Transmission through an helix-shaped molecule in the presence of a dipole field. (Top left) In the presence of SOC, the amplitude of the (exact) electronic wave function in its tail (parametrized by ξ ≫ 1) grows as a function of the angular momentum. Moreover, the spin is aligned along the momentum direction (see inset), and as a consequence, the state has a well-defined helicity. (Top right) The increased amplitude deep inside the molecule gives rise to an enhanced transmission probability that grows with the angular momentum . The scattering matrix¹²⁸ is derived for the exact wave function. This panel shows that the enhanced transmission for is accompanied by a spin polarization (inset). (Bottom left) Similar results were obtained using a tight binding calculation for a molecule with the same parameter but somewhat different length. (Bottom right) Deforming the molecule to have a larger pitch or radius helps spin polarization. All panels adapted with permission from ref (127). Copyright 2019 American Chemical Society.

For helical molecules with delocalized electronic states, but no dipolar potential, the energy window where strong spin-dependent transport is observed is determined by a partial energy gap of ∼1 meV. When a dipole potential is introduced, this energy window is instead determined by the dipole energy of ∼0.1 meV and the transmission probability of polarized electrons is enhanced (see Figure 15). This result is in agreement with experimental observations that the total transmission decreases with increasing molecule length, while the spin polarization increases.

Ghazaryan et al. recently developed an analytical model for CISS, modeling a chiral molecule as an anisotropic wire with a dipole field not particularly aligned along a specific molecular axis.¹²⁹ While the model does not assume a helical architecture, the dipole field was found to be critical in this case in order to determine the chirality of the system via the relative orientation of electric dipolar components and the anisotropic wire potential. In this way, this simplified model shows that nonhelical chiral molecules can be used to capture spin selectivity, which has been observed in experiments using molecules containing just a single chiral center. Moreover, it can explain the change in sign of spin-dependent transfer experiments resulting from cold denaturation of peptides, which change from native α-helical conformations to stretched, linear stuctures, resulting in a reversal of the dipole direction.³⁹ Thus, using the electric dipole moment as a tuning knob or switch for spin selectivity may establish avenues for molecule-based devices in which enantiomeric substitution is not possible or where material manipulation with external magnetic fields is problematic.

Orbital Polarization Effect and Molecule–Electrode Interface Effect

The unusual, apparently large SOC in organic systems has not been explained satisfactorily yet by theory, but alternative mechanisms to study the effects of the substrate and spinterface have been developed recently. Liu et al. suggest the concept of orbital polarization effects (OPE) and proposed that the SOC in the normal metal electrode converts the orbital polarization into a spin polarization.¹³⁰ As shown in Figure 16a, the SOC only exists in the leads rather than in the chiral molecules. The chiral molecules act as both an orbital polarizer and an orbital filter of the orbital polarization from the leads. It is also suggested that achiral materials with breaking inversion-symmetry can lead to spin selectivity with the OPE.

Figure 16.

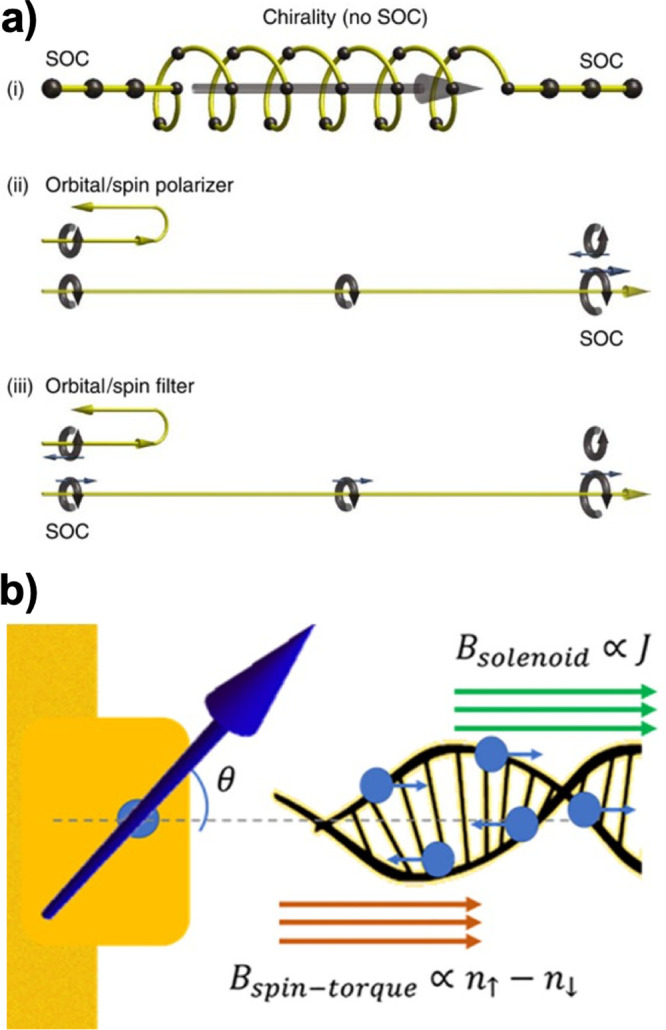
(a) Schematics of the orbital polarization effect. (i) A chiral molecule is connected to two leads on each end and (ii) acts as both an orbital polarizer and (iii) an orbital filter. The half circles with arrows represent the orbital and thin arrows represent the spin.¹³⁰ Adapted with permission from ref (130). Copyright 2021 Springer Nature. (b) Schematics of the description of the origin of the chiral-induced spin selectivity effect. The interface orbital magnetization is indicated by the blue arrow at a tilted angle. It interacts with two effective magnetic fields: the solenoid field and the spin-torque field.¹³¹ SOC: spin-orbit coupling. Adapted with permission from ref (131). Copyright 2021 American Chemical Society.

Alwan et al. suggest that CISS originates from the interplay between large SOC in the electrode and a CISS-induced solenoid field and spin-torque field in molecules (illustrated in Figure 16b).¹³¹ At the interface between a metal with large SOC and chiral molecules, effective magnetization arises from the interface orbitals. Applying a current through the chiral molecules generates a solenoid field inside, which produces a small tilt in the magnetization. The tilt causes a spin torque effect that further tilts the magnetization. At steady state, the effective magnetic field at the spinterface is composed of a small solenoid field and a large spin-torque field, which leads to spin filtering. The theory of spinterface origin of CISS can account for key experimental observations and provide predictions that can be tested experimentally.

Magnetic Exchange Interactions

Recent experimental^57,60 and theoretical^14,91,132 studies suggest that electronic exchange interactions may play fundamental roles in combination with the SOC,¹³² due to the antisymmetric nature of the electronic wave function and the influence of many-body effects. Exchange interactions play key roles in molecular recognition of chiral species, in addition to van der Waals interactions, and under some conditions, for example, short intermolecular distance, exchange can dominate SOC in inducing a molecular magnetic response that contains the CISS and exchange component as well as intersystem crossing terms that are specially relevant in photoinduced ET reactions. While the sources of exchange splitting in chiral molecular systems are not yet established, potentially arising from electron–phonon interactions (see below) and many-body effects, these exchange interactions can be understood as significant nonequivalence between spin-dependent channels, and as a way to couple the molecule to external spin moments, generating magnetic anisotropy. Exchange-related intermolecular interactions in arrays of helical molecules were shown to stabilize the broken spin symmetry (polarized singlet) state, while the effect is absent in linear molecules.^14,90 When molecules come into contact with ferromagnetic surfaces, the electronic exchange must play critical roles in the molecular response. As a consequence, subsequent interactions with magnetized surfaces can facilitate symmetry breaking between enantiomers and may lead to enantiomeric discrimination, which would be mediated by exchange interactions. Further indications of the relevance of exchange contributions were found in ref (91): Changing the amount of Hartree–Fock exchange included in exchange–correlation functionals strongly influences the magnitude of the computed spin polarization in model helical molecular junctions. This points out the need for systematic investigations of the roles played by electronic correlation and exchange effects in the self-consistent response involved in the description of conductance in chiral junctions and ET in chiral molecules. The inclusion of magnetic exchange interactions may also be relevant for understanding the coexistence of spin polarization and spin coherence, an important subject in QIS.

Vibrational Contributions to Spin-Dependent Transport

In electronic propagation through molecules at room temperature, electron–vibration interactions can enable transitions to higher energy states that allow greater spatial delocalization. Coherence in charge transport, such as in tunneling, hopping, or intermediate regimes, is linked to thermal activation. A recent theoretical study by Diaz et al. examined the influence of disorder and decoherence on spin polarization in helical systems.¹³³ As a mimic of low-frequency vibrations, static Anderson diagonal disorder was included in their model. At nonzero temperatures, this disorder was found to be crucial to produce length- and temperature-dependent spin polarization. Du et al. also examined the influence of vibronic interactions in spin-selective transport in a model of double-stranded DNA, finding that this interaction enhances CISS by revealing stronger spin polarization and reveals spin-dependent channels of transmission throught the molecular bridge with increasing vibrational frequency.¹³⁴ Moreover, the vibrationally induced transmission modes are robust against dephasing, which would lead to loss of electron phase and defined spin memory.

Connections have been drawn recently between vibrational contributions to CISS, magnetic exchange interactions, and electron correlations.¹³² Molecular vibrations can generate electron correlations that disrupt the molecule’s electronic structure, where electron–electron interactions give rise to exchange interactions between spin channels in electron transport. Fransson modeled spin-dependent electron–phonon coupling, where electron–phonon-assisted SOIs are shown to have a significant effect on the spin selectivity of electron transport in chiral structures.¹³⁵ In the context of molecular contact with metallic surfaces, Fransson also presented a theory that molecular vibrations in the combined chiral molecule–metal configuration are responsible for spin selectivity due to vibrationally supported correlation-induced exchange.¹³⁶

Tied to the hypothesis that (thermally activated) molecular vibrations contribute significantly to CISS is the idea that conformational change and molecular deformations can play a role and be used as a way to experimentally probe spin-selective transport. A minimal model for DNA, with details of the relation between geometry and transport eigenstates, recently led to a proposal that mechanical deformations may be used to assess the orbital involvement in spin transport.¹³⁷ Strain-induced changes to molecular geometries can be feasibly induced in, that is, c-AFM or scanning tunneling microscopy (STM) break-junction measurements.

The Role of Coherence

Coherence is a hallmark of quantum phenomena. It enables the communication between spins and extended superpositions necessary for quantum computing applications. The role of coherence and decoherence in spin-polarized transmission and in charge transfer due to molecular adsorption at surfaces remains poorly understood in the context of CISS mechanisms, where it arises in biological systems, and how it may be leveraged for quantum information processing. All models proposed for CISS focus to some extent on quantum coherence, although nonunitary effects (i.e., arising from electron leakage to the environment) have been considered.¹¹³ Since CISS occurs at room temperature, how do coherent quantum mechanical effects survive? Generic voltage–probe leakage is a minimal model to examine decoherence effects. In fact, such probes have been shown to be a route to spin polarization, as breaking time reversal symmetry would indicate. A more explicit model for decoherence would include the electron–phonon coupling as a major decoherence mechanism^113,138,139 and describe how electronic and spin degrees of freedom couple to the phonon bath in the tunneling process. Analysis finds partial electron–phonon decoupling to first order in the longitudinal modes,¹⁴⁰ while the coupling persists for optical modes in DNA. This decoherence mechanism could also operate in oligopeptides. All of the theoretical and computational tools associated with this approach are prepared to assess the influence of spin–phonon coupling in ET and transport in chiral molecules.

Future models will need to include the two main mechanisms involved in charge transport in chiral biological molecules and polymers: tunneling and hopping.^142,143 Which mechanism dominates transport depends on the coherence of the transport and Peierls-like instabilities.¹⁴⁴ A simple model for nearly filled orbitals underpins a proposed mechanism for CISS based on spin-selective transmission under a barrier,¹⁴¹ as shown in Figure 17. The mechanism is based on the torque-coupled interplay between electron spin and molecular angular momentum; both tunneling and hopping could be strongly influenced by spin polarization modifying the effective coherence length of ET. A recent study, however, suggests that the proposed model does not lead to CISS or any net spin polarization,¹⁴⁵ and further theoretical considerations are needed to describe the mechanisms underpinning CISS.

Figure 17.

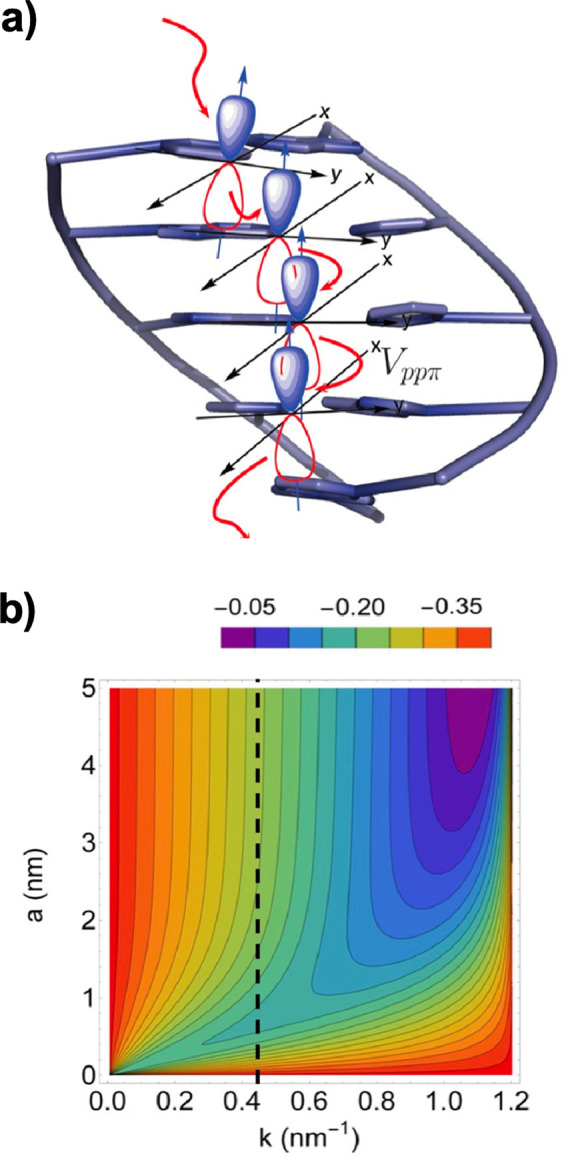
Spin-orbit interactions and spin selectivity for tunneling electron transfer in DNA. (a) Schematic of DNA molecule with orbitals for electron transport. The p_z orbitals are perpendicular to the base planes and coupled by V_ppπ Slater–Koster matrix elements. (b) Plot of spin asymmetry P_z as a function of scattering barrier length a and input momentum k. Adapted with permission from ref (141). Copyright 2020 American Physical Society.

There are not yet experimental reports characterizing or quantifying the electron spin coherence lifetimes associated with CISS inside a chiral molecule. Measuring these chiral selective properties is critical for evaluating their robustness to support strong spin polarization, including coupling to external degrees of freedom in open environments.

Chiral Light–Matter Interactions

Recent correlations were drawn in experiments between the interactions of chiral matter with chiral light, and electron spin polarization in ET between chiral-molecule–functionalized nanomaterials.³⁴ Moreover, models related the strength of spin polarization in electron transport through chiral molecules to the molecular polarizability,⁶⁶ which can relate the CISS effect directly to optical activity of chiral molecules. Thus, understanding and developing more efficient ways to control chiral light–matter interactions can be motivated by promising avenues toward quantum applications for manipulating electron spin dynamics with light and transducing spin information into photons.

The chirality of light is described by the rotation of electric and magnetic fields as the wave propagates or by the helical geometry imprinted on the wavefront, and these effects are attibuted to photon spin and orbital angular momentum (OAM), respectively. The photon’s spin angular momentum is quantified as ±ℏ per photon with the sign corresponding to left- and right-handed circular polarizations, while the OAM is quantized as lℏ per photon, where l is the topological charge with sign dependent on the twist direction of the optical vortex. The propagation of light in the presence of chiral matter and the matter–light interactions (i.e., scattering and absorption) are also dependent on the broken space inversion symmetry of the matter. Spin-dependent effects (referring to left- and right-handed circular polarization of radiation) have been explored since the discovery of optical rotation by Arago and Biot in the early 19th century and observations of CD by Wilhelm Karl von Haidinger. By representing linearly polarized light as a coherent superposition of left-handed and right-handed light, optical rotation can be rationalized as a phase shift of left-handed photons with respect to the right-handed photons due to their different indices of refraction when traversing chiral materials, also known as circular birefringence. Similarly, CD is the preferential absorption of photons of one particular circular polarization.¹⁴⁶ The differential absorption of circularly polarized light depends on the imaginary parts of the electric, magnetic, and chiral polarizabilities.

The OAM of photons also provides an optical degree of freedom that gives rise to spin–orbit effects and helical dichroism. Treatments of chiral light–matter interactions have generally excluded these effects. That is, in the description of CD, the topic of whether light with OAM can interact selectively with chiral matter in the dipole approximation has been widely debated.¹⁴⁷ However, by including higher-order modes (such as electric quadrupole), OAM-based chiral light–matter interactions should be possible and could even amplify or shift CD responses.¹⁴⁸

In this section, we highlight recent advances in strategies to amplify the enantioselective interactions between light and matter using plasmonic and dielectric platforms to control intensity, phase, and polarization of electromagnetic near fields.^149−151 We also describe physiochemical mechanisms by which chirality can be transferred such as via electromagnetic interactions, conformational changes, and chiral assemblies which provide exciting prospects for biosensing and chiral chemical analysis.¹⁵² Finally, we touch on cutting-edge experiments and experimental prospects for using OAM for quantum information protocols.¹⁵³

Nanotechnology Approaches to Enhance Chiral–Optical Properties

Subwavelength photonic architectures, including plasmonic^154,155 and all-dielectric nanoparticles^156,157 and arrays, provide means to amplify enantioselective absorption for chiral chemical analysis. The capability to sculpt electromagnetic fields to tailor these chiral–optical properties can be understood semiclassically (see refs (158 and 159) for theory casting both radiation and matter in general quantum form). The differential absorption intensity is often referred as Kuhn’s dissymmetry parameter , where A₊ and A_–are the absorption intensities of the chiral material when illuminated by left- and right-handed circularly polarized incident fields, respectively (quantum mechanically referring to a photon’s spin angular momentum). The absorption intensity for left (+) and right (−) handed circularly polarized fields by a chiral molecule can be expressed as^16,160

1

where E⃗ and H⃗ are the complex electric and magnetic fields, ω is the frequency of light, μ₀ is the permeability of free space, and α″, χ″, and G″ are the imaginary parts of the electric, magnetic, and chiral polarizabilities of the chiral molecule. C is the so-called electromagnetic density of chirality:

2

Assuming that the μ₀²χ″ |H⃗|² is negligible due to the weak magnetic polarizability of most small molecules, combining eqs 1 and 2, Kuhn’s dissymmetry parameter can be recast as

3

Similarly, the CD spectra of molecules, defined as CD = A₊ – A_–, can also be reformulated as

4

The first term in eqs 3 and 4 depends exclusively on the intrinsic polarizabilities of the molecules. In contrast, the second term in eq 3 corresponds to a purely electromagnetic quantity, which can be engineered optically. The optical chirality of electromagnetic fields, a pseudoscalar field quantity, was derived by Lipkin in 1964.¹⁵ In 2010, Tang and Cohen quantified optical chirality density theoretically¹⁶ and experimentally¹⁶¹ and demonstrated how these enantioselective enhancements could be used to manipulate chiral-selective excitation rates of chiral molecules. While in the far field, optical chirality is limited to that of freely propagating circularly polarized light, in the near field, C, and therefore g, can be amplified using nanophotonic structures. Efforts in this direction have since triggered a myriad studies of electric and magnetic field-enhanced chiral–light matter interactions using both plasmonic and dielectric nanomaterials.

Plasmonic and Magneto-Plasmonic Materials

The nanoconfined amplification of electric fields attributed to plasmonic excitation has been widely studied beyond the physics and nanophotonics communities due to its broad applicability in sensing and spectroscopy,^162,163 energy conversion,¹⁶⁴ nanomedicine,^165,166 and many other areas.¹⁶⁷ Specifically, the field of chiral plasmonics grew rapidly in the past decade to manipulate electromagnetic fields or to provide more sensitive detection platforms for chiral molecule analytes.⁴ Plasmonic effects in nanostructures are due to their strong electric polarizabilities, giving rise to localized surface plasmon resonances.¹⁶⁸ Thus, electromagnetic near-fields of plasmonic nanoparticles support large electric field enhancements. However, magnetic field enhancement with such nanostructures is limited because the magnetic polarizability of these structures is typically small. Therefore, to enhance C, these structures typically must be designed to generate circulation of the free electron cloud upon excitation of plasmon resonances to induce magnetic field enhancement in the near field (Figure 18a). This enhancement creates a magnetoelectric dipole moment in the nanostructure, and the resulting phase shifts between electric and magnetic fields give the near field chiral character.

Figure 18.

(a) Scanning electron microscope (SEM) image of a platinum chiral nanohelix grown by focused ion beam induced deposition (FIBID) and a 3D representation of current oscillation induced by exciting on resonance for the right- and left-handed resonance modes.¹⁸³ Adapted with permission from ref (183). Copyright 2015 American Chemical Society. (b) Strongly enhanced optical chirality density (C) theoretically predicted to be generated within plasmonic helices.¹⁷⁰ Adapted with permission from ref (170). Copyright 2014 American Chemical Society. (c) SEM images of left- and right-handed planar chiral coupled nanorod antennas and experimentally measured chirality flux efficiency for each configuration.¹⁷⁸ Adapted with permission from ref (178). Copyright 2018 American Chemical Society. (d) Optical chirality density enhancement, electric field enhancement, and circular dichroism (CD) calculated for pure left- and right-handed as well as racemic mixtures of plasmonic gammadion arrays.¹⁸¹ Adapted with permission from ref (181). Copyright 2018 American Chemical Society.

In many cases, achieving amplifications in C requires three-dimensional (3D) structures, which give extremely large optical activity and C enhancement (Figure 18b),^169−171 but can be extremely challenging to fabricate at the nanoscale. These procedures may require serial lithography such as for arrangements of “meta-atoms” in oligomer-type structures¹⁷² or direct laser writing¹⁷³ to create helical metallic geometries. Advanced lithographies using glancing-angle deposition,^174,175 substrate deformation, and templated colloidal assembly^176,177 may also be used. Alternatively, planar chiral structures with 2D geometric chirality are easier to fabricate, and can be used to enhance C (Figure 18c).^178−180 Similar to 3D architectures, large amplification of near-field C can be realized locally, but the sign can vary spatially over the surface. A common challenge for chiral molecule sensing is to deconvolute the intrinsic chiral–optical background that these plasmonic nanostructures exhibit. García-Guirado et al. showed that racemic nanoplamonic arrays could overcome this obstacle by eliminating a CD background while maintaining C enhancement (Figure 18d).¹⁸¹ Achiral plasmonic nanoarchitectures may also be used,¹⁸² but the mechanism for chiral–optical detection relies on far-field effects rather than near-field C enhancement and is related to chirality imprinting as discussed in greater detail below.

Plasmonic nanoparticles can also be designed using solution-based chemical synthesis with intrinsic chiral geometries or bottom-up self-assembly approaches.^184,185 These systems are particularly attractive for biosensing applications that may rely on local C enhancement for chirality detection in vitro or in vivo. Enantioselective growth pathways of nanocrystals can be achieved, for instance, using templated growth by exploiting different binding energies of l- vsd-amino acids or short peptides on different crystalline facets.^186,187 Achiral nanoparticles can also be assembled into 3D chiral structures using chemical functionalization, that is, using protein or peptide modification^188,189 or via more widely used DNA nanotechnology.^190−195 These assemblies are also often reconfigurable, enabling external control of enhanced chiral–optical responses with external stimuli. Plasmonic nanoparticles assembled using chiral molecules could potentially serve as useful systems to test if spin-dependent electron flux through chiral linkers may influence plasmonic chiral–optical responses.¹⁹⁶

Hybrid platforms that incorporate magnetic nanoparticles or thin films could also be useful for both chiral sensing and control of electromagnetic chiral responses. The combined magneto-optical and chiral–optical activity can significantly enhance the interactions between left- vs right-handed circularly polarized light with nanostructured surfaces and provide a facile way to tune chiral–optical responses with an external magnetic field. Armelles et al. demonstrated magnetic field-controllable changes of chiral–optical effects in Au gammadions that incorporated ferromagnetic Co layers.¹⁹⁷ Deconvolution of both magneto-optical and chiral–optical contributions to the electromagnetic field interaction was later shown in hybrid platforms of magnetic Au/Co multilayer films and chiral Au plasmonic oligomers.¹⁹⁸ Enhancements in far-field chiral–optical responses exceeding 100% were also achieved with magnetic field modulation with bimetallic Au and Ni nanoantenna arrays.¹⁹⁹ Dielectric nanophotonic platforms, discussed in greater detail below, that incorporate ferromagnetic materials have also shown promise for these applications.^200,201

Dielectric and Nanophotonic Materials

Dielectric nanoparticles with high refractive index support both electric and magnetic multipolar Mie-type resonances upon light excitation. These modes can be individually addressed and tuned in nanoscale resonators to control chiral–optical properties.²⁰² Importantly, using dielectric nanostructures, it is possible to obtain single-sign enhancements in the optical chirality density in evanescent fields using dipolar modes under Kerker-like conditions where transmission approaches unity.²⁰³ Under these conditions, when electric and magnetic dipolar fields remain strong and are tuned to the same frequency, the fields maintain incident polarization when irradiated with circularly polarized light, which can greatly enhance optical chirality density. Even larger enhancements in C occur near multipolar magnetic resonances. However, the sign of C is not uniform in the near field, as the phase of the resulting standing wave varies across the surface.²⁰⁴

Unlike plasmonic systems, dielectric nanoparticles need not possess 3D or planar chirality themselves to support local amplification of C because of their stronger and more easily addressable magnetic multipolar modes. These structures therefore can be fabricated using simpler techniques than the more elaborate methods required for preparing asymmetric plasmonic metal antennas. Importantly, achiral nanophotonic structures can be used to boost enantioselective absorption by chiral molecules, which removes the intrinsic chiral–optical response of chiral nanophotonic platforms typically used in plasmonic systems. High-refractive index spherical nanoparticles can provide 1 order of magnitude or higher CD enhancement factors (Figure 19a).^204−206 Furthermore, the (usually very inefficient) asymmetric photoseparation of chiral enantiomers^207,208 can also benefit from enhanced chiral light–matter interactions. High-refractive index nanostructured materials have shown great potential to selectively induce photolysis and ionization of particular chiral enantiomers, while leaving the mirror image almost unaffected^204,209 (Figure 19b). Even more promising are periodic arrays of dielectric cylindrical disk geometries, which allow independent tuning of magnetic and electric dipolar modes by changing disk heights or radii.^209,210 Following computational demonstrations of enhanced optical chirality density with these structures, such dielectric nanodisk arrays were shown experimentally to enhance CD of evaporated organic films of chiral small molecules and SAMs of DNA (Figure 20).^149,211 However, the chiral–optical enhancement mechanisms afforded to CD signals are not clear, and more work is needed to establish the relative roles of electric and magnetic dipolar resonances, and the influence of total, partial, or minimal overlap with molecular absorption spectra.

Figure 19.

(a) Nanoparticles can enhance molecular circular dichrosim (CD) spectroscopy. A 75 nm radius silicon nanosphere is illuminated from below by λ = 625 nm circularly polarized light. The figure depicts the CD enhancement factor at a plane crossing the center of sphere. (b) When Kuhn’s dissymmetry factor is increased in the vicinity of a nanoparticle, the enantiomeric excess achievable in a photochemical reaction increases dramatically for a given extent of reaction. (Inset) Spatial distribution of dissymmetry factor enhancement for a 536 nm Si sphere at λ = 1391.82 nm. In the presence of a Si nanosphere, in a region where g ≈ 7, a 20% enantiomeric excess can be reached with a yield of 50% compared to the 1% achievable in the absence of the nanoparticle. Panel (a) adapted with permission from ref (205). Copyright 2013 American Physical Society. Panel (b) adapted with permission from ref (204). Copyright 2017 American Chemical Society.

Figure 20.

(a) Scanning electron micrograph of a Si nanodisk array coated with a ca. 200 nm phenylalanine layer. (b,c) Experimentally measured circular dichrosim (CD) and extinction spectra of Si nanodisk sensor arrays functionalized with phenylalanine coatings. Panels (a–c) adapted with permission from ref (211). Copyright 2020 American Chemical Society. (d) Experimental schematic of fluorescence-detected circular dichroism (FDCD) using Si nanodisk arrays modified with self-assembled monolayers of chromophore-functionalized DNA molecules. (e) Experimentally measured FDCD and enhancement in optical chirality density for increasing disk sizes when functionalized with DNA monolayers. Panels (d,e) adapted with permission from ref (217). Copyright 2020 American Chemical Society.

Low-loss dielectrics that support high-quality factor (high-Q) resonances have also shown considerable promise for increasing the strength of chiral light–matter interactions, supporting resonances with extremely long lifetimes when excited.²¹² A promising approach to generate chiral-selective high-Q modes uses symmetry manipulation in periodic arrays of resonators.^213,214 Recent calculations by Hu et al. on biperiodic disk lattices of diamond showed enhancements of C by over 3 orders of magnitude in the UV by coupling to high-Q asymmetric electric and magnetic dipole resonances.²¹⁵ Chen et al. proposed a method for integrated molar chiral sensing based on high-Q TiO₂ metasurfaces to determine enantiomeric ratios.²¹⁶ The choice of materials in these examples is critical to avoid strong damping of the optical modes due to losses in the near-infrared, visible, and near-UV regimes, where most organic chiral molecules exhibit strong absorption. Further theoretical and experimental studies of the strong coupling afforded by high-Q modes when overlapped with or in spectral proximity to chiral molecular resonances will likely provide insights into mechanisms to enhance enantioselective absorption for chiral sensing and separations as well as spin selectivity in molecular electronic structures.

Chirality Transfer and Imprinting in Functionalized Nanomaterials

Handedness can be transferred from a chiral object to an achiral object or achiral medium, that is, chiral molecules adsorbed on surfaces induce chirality on the substrate. Indeed, theoretical analyses have found that CD and optical rotatory dispersion signatures can be induced through chiral imprinting.^218−220 In fact, it is possible for the magnitude of the imprinted chiro-optical signature to be larger than that of the chiral adsorbate itself.

A kind of handedness can be imparted to excited states using circularly polarized excitation. For example, molecules with degenerate x- and y-polarized excited states, when excited by left- vs right-handed circularly polarized light wave functions, are complex conjugates of one another. If the excited state induces chemistry on a time scale that is fast compared to the time scale of decoherence, the chemistry may be imprinted by the handedness of the light excitation. For example, Skourtis et al. predicted that ET yields can be influenced by the handedness of circular excitation.²²¹ Combining circularly polarized excitation with chiral bridges can thus affect ET chemistry.^34,222

Chirality Transfer in Raman Optical Activity

Recently, it was discovered that electromagnetic chiral interactions could be used to transfer chirality information from a chiral molecule to an optically inactive (achiral) Raman reporter molecule. Transfer of chirality is known to occur between molecules through chemical bonds.²²³ However, in 2015, Ostovar pour et al. showed in a seminal article that chiral information could be transferred from a chiral molecule to an achiral one in the presence of a plasmonic nanosphere (Figure 21a,b) irradiated by circularly polarized light at its resonant frequency.²²⁴ The transfer of chiral information was demonstrated through a Raman optical activity (ROA) experiment. The chiral molecules in the experiment were Raman inactive, while the achiral molecules displayed a strong Raman response. In the absence of chiral molecules, the plasmonic nanoparticle-Raman reporter molecule hybrid did not present any ROA signal. Nevertheless, when the non-Raman active chiral molecule was added to the system, the experiment presented a strong ROA signal.¹⁷ Since the chiral molecule and the Raman reporter molecules were spatially well separated, this chiral information transfer could not occur through the formation of a chemical bond between the chiral and the achiral system; it had to be mediated by the plasmonically enhanced electromagnetic interactions.

Figure 21.

(a) Schematic of the plasmonic nanoparticle–chiral molecule hybrid. The silver nanoparticle is surrounded by reporter Raman-active molecules, surrounded by a silica shell and has attached a chiral analyte. The middle plot shows surface enhanced resonant Raman spectra of d- and l-tryptophan bound to the benzotriazole-functionalized nanotag, which are identical as expected for the two enantiomeric systems. Surface enhanced Raman optical activity spectra in the presence of the two chiral enantiomers. Strong chiroptical responses in several signals are observed, demonstrating the chirality transfer phenomena. (b) Schematic of the model describing the chiral molecule–nanoparticle hybrid. Step 1: Circularly polarized light excites the plasmonic nanoparticle. Steps 2a and b: The plasmonically enhanced fields excite the chiral molecule, which backscatters light into the particle, producing a self-consistent chiral polarization of the plasmonic particle. Step 3: The chiral polarization of the chiral molecule–nanoparticle hybrid excites the nonchiral Raman-active reporter molecule. Step 4: The Raman-active molecule emits a surface-enhanced resonant Raman signal, which is different for left handed (M⁺) and right handed (M^–) circularly polarized incidence, creating a measurable Raman optical activity signal. Panel (a) adapted with permission from ref (17), based on work in ref (224). Copyright 2015 Springer Nature. Panel (b) adapted with permission from ref (225). Copyright 2020 American Chemical Society.

These experiments were later addressed theoretically and explained on the basis of enhanced chiral-light matter interactions.²²⁵ In the first step, the plasmonic nanoparticle is excited by the circularly polarized incoming beam (step 1 in Figure 21c). Then, the plasmonic resonant response of the particle produces enhanced fields in their surroundings. These enhanced near fields excite the nearby chiral molecules following eq 1, as depicted in step 2a in Figure 21c. Since the plasmonic nanoparticle is not chiral, it does not induce any additional chirality in the electromagnetic response around it. Nevertheless, the excitation of the chiral molecule in its surroundings filters the spin of the exciting fields, absorbing photons of one particular handedness more efficiently. As a result, the back scattering of the fields from the molecule to the particle, step 2b in Figure 21c, induces a chiral electromagnetic polarization in the plasmonic particle. Lastly, these fields excite the nonchiral Raman molecule (Figure 21c, step 3), which yields a measurable Raman signal, denoted as M⁺, in the far field. From the point of view of symmetry arguments, the main ingredient of this model is that inversion symmetry is broken at the interface between the chiral molecule and the plasmonic nanoparticle.

Furthermore, exciting the plasmonic-nanoparticle chiral-molecule hybrid with a circularly polarized incoming beam of the opposite handedness will induce a different optical response in the system due to the specific handedness of the chiral molecule. As a result, the Raman molecule will now be excited by electromagnetic fields of a different intensity. That is, the field will become “chiralized”, resulting in a different Raman signal in the far field. Since the ROA signal is given as ROA = M⁺ – M^–, the nonchiral Raman reporter molecule will now produce a measurable ROA signal due to its excitation by the radiated chirality-information carrying electromagnetic field from the plasmonic-nanoparticle chiral-molecule hybrid (step 4 in Figure 21c).

In summary, it has been shown that hybrid systems composed of a nonchiral plasmonic nanoparticle and a chiral molecule behave distinctly with respect to the left- and right-circularly polarized incident light at the frequency of the plasmonic resonance. Indeed, since the chirality of the molecule preferentially enhances the intensity of the incident light with one spin (polarization) over the other one, the intensity of the electric part of the back radiated light’s electromagnetic field at the position of the nonchiral Raman active probe depends on the combination of the incident handedness and the chirality of the Raman inactive molecule of the hybrid system. Ultimately, this difference is sensed by the Raman-active nonchiral molecule because its Raman signal’s intensity is proportional to the fourth power of the sensed electric field’s intensity.

Thus, we have seen that chirality induces spin selection of the light shining on hybrid systems containing plasmonic and chiral species and that the information about the selected spin can be transmitted by the back radiated electromagnetic field over long distances, where it can be decoded by a Raman-active nonchiral molecule. This chiral-induced spin selectivity constitutes, therefore, a highly efficient method to transmit and decode information about chirality over large distances, which includes the nanoscale. The implications of this chirality transfer for the design of devices, for electron–phonon information transfer, and for the field of photoinduced spin-dependent chemistry are promising.

The use of artificial chiral nanostructures such as arrays of plasmonic and dielectric objects can be explored in the future for their use in similar spin interactions. For example, nanoparticles, arrays of nanodisks and holes, and photonic metasurfaces have been shown to exhibit electric and magnetic resonances for enhancing chiral optical density^149,226 and would be excellent candidate materials for chiral spin selection. These types of nanophotonic materials have the benefit of ease of scalable fabrication and independently tunable properties based on their materials and geometries.

Chiral Imprinting in 2D Materials

Chirality in 2D materials has spanned diverse compounds and structures, including graphene quantum dots (GQDs),²²⁷ nanodisks,²²⁸ and nanoribbons,^229−233 nanoplatelets of CdSe,²³⁴ MoS₂ layers,²³⁵ colloidal semiconductor quantum wells of different types,²³⁶ and transition-metal dichalcogenide semimetals.²³⁷ One of the earliest systems to show chiral properties in strictly 2D was graphene flakes or QDs (GQD) covalently modified by l- or d-cysteine moieties.²²⁷ By using edge modifications via aqueous dispersions, Suzuki et al. showed that chiral amino acids can induce excitation bands with specific features in the CD spectra at 210–220 nm and 250–265 nm (Figure 22a). Comparing the optical responses for l/d-cysteine bound to GQDs (l-GQD and d-GQD), a clear asymmetry is found in the new bands that can be correlated with structural deformations of the graphene layer itself. Once the ligands were linked to the edges, an increase in the buckling deformation of the GQD was observed. That is, depending on which amino acids is present at the edges, the GQDs have a right- or left-handed twist (Figure 22b). The buckling is due to noncovalent intermolecular interactions of the amino acids with each other and also with other parts of the edge. Indeed, it is well-known that deformations in chiral regions of large molecules tend to propagate the chirality through other regions or host environments such as proteins, polymers, or liquid crystals.^5,238 With l-/d-GQDs showing chiral properties, one can explore different pathways for biological recognition in functional cells, for example, neurons,^239−241 bone marrow cells,^242−245 or immune cells.^246,247 In particular, l-/d-GQDs show biocompatibility with human liver hepatocellular carcinoma cells where different toxicity between the chiral GQDs was observed.²²⁷ Although it is not clear why such differences emerged, a few factors associated with the chirality of the ligands and the twists of the graphene sheets may play roles.

Figure 22.

(a) Circular dichroism (CD) and optical absorption spectra for l-graphene quantum dot (l-GQD, red) and d-GQD (black) dispersions. (b) Schematic of the structures of d-GQD and l-GQD on a 3 nm QD. The rotation direction of the helices is opposite to the handedness of the edge ligands. (c) CD spectra of d-/l-cysteine functionalized MoS₂ after exfoliation. Similar results for d-/l-penicillamine were obtained (not shown here). (d) Diagram of the deformations generated by molecular functionalization of d-penicillamine inducing chirality on MoS₂ layers. (e,f) Frequency shifts of the d- and l-Cys-MoS₂ QDs/Cu²⁺ sensors exposed to (e) 5 mM d-Tyr and (f) 5 mM l-Tyr solution. Panels (a,b) adapted with permission from ref (227). Copyright 2016 American Chemical Society. Panels (c,d) adapted with permission from ref (235). Copyright 2018 American Chemical Society. Panels (e,f) adapted with permission from ref (248). Copyright 2018 American Chemical Society.

Building on these studies of chiral molecules modifying and associating with 2D materials, liquid exfoliation of layered materials using chiral molecules, for example, l-cysteine and d-penicillamine, resulted in chiral thin layers of MoS₂.²³⁵ Purcell-Milton et al. reported that MoS₂ shows strong CD after ligand functionalization (Figure 22c). The optical spectra display a near-mirror image relative to the wavelength considered with the different molecules bound to the surface. The characteristic changes of the CD when varying optical orientation between positive and negative signs as function of the wavelength is due to the Cotton effect. Other amino acids, such as glutamic acid, alanine, and methionine, were also tested by Purcell-Milton et al., but none of them resulted in chirality of the MoS₂ layers. This result suggests that a ligand coordination as well as binding through at least two functional groups should take place at the surface.²⁴⁹ One of the implications of having sizable interactions between l-cysteine and d-penicillamine and MoS₂ is the structural deformation of the nanosheets with the functionalization (Figure 22d). That is, an achiral MoS₂ layer can be transformed into a chiral sheet. This argument was used to model the optical spectra of both molecules on MoS₂ resulting in close agreement with the experimental results.

The utilization of liquid exfoliation using chiral molecules provides large scale production of TMDs with chiral features. In principle, such a strategy can be extended to many layered materials (e.g., MoSe₂, WS₂, and WSe₂) with applications for sensing or optical devices. For instance, in enantioselective catalysis and peroxidase activity,²⁴⁸ Zhang et al. demonstrated that MoS₂ layers functionalized with d-, l-cysteine (d-Cys-MoS₂, l-Cys-MoS₂) show enantioselective peroxidase activity on chiral substrates composed by d- and l-tyrosinol (Tyr) enantiomers (Figure 22e,f). With the assistance of copper ions (Cu²⁺), both d-Cys-MoS₂ and l-Cys-MoS₂ systems display higher oxidation of d-Tyr (Figure 22e) and l-Tyr (Figure 22f) beyond that found in the unmodified MoS₂ QDs. Indeed, no peroxidase activity is observed for time scales of 10 min for pristine MoS₂. This result suggests that modified 2D materials can function as nanozymes with enantioselectivity.

Chemical Chirality Control in Hierarchical Assemblies

Control of structural chirality is well within the chemical toolbox. Building chirality into the chemical bond-network realizes persistent chirality in the organization of structural building blocks and their supramolecular assemblies. These assemblies then manifest in complex engineered and biological networks. Such supramolecular chemistry can be combined with semiconductors to imprint chiral interactions into extended electronic structure. Therefore, we hypothesize that chemical bond chirality will continue to be the primary substrate resource by which chiral degrees of freedom will be realized and controlled. Here, we describe how such degrees of freedom may be introduced into extended materials.

Supramolecular aggregates often assemble into helical and twisted geometries. Steric and π–π interactions among molecules favor 1D or quasi-1D structures, for which a chiral center or solvent will favor a specific twist.²⁵⁰ Such structures can, in turn, seed more complex superstructures with twisted geometries.²⁵¹ These structures can be easily characterized using CD, though the interpretation of CD signals in extended excitonic systems is challenging.²⁵² Nevertheless, molecular assembly inducing or enhancing chirality represents an important potential control knob for creating chiral nanophotonic materials.

CD spectroscopy also revealed surprising emergent chirality, even in systems whose building blocks are fully achiral. The appearance of chirality in these systems comes from a thermodynamic instability in assembly that leads to unequal numbers of opposite handed superstructures.²⁵³ Chirality in these systems can also be seeded by chiral impurities. Therefore, realizing highly ordered and dense chiral networks may arise naturally in the study of supramolecular architectures.

One may be able to assess the effect of supramolecular organization by studying the chiral excitonic response through electronic CD.²⁵⁴ For electronic transitions, transition dipole moment coupling (and accompanying extended delocalized excitons) creates a system response which “feels” the chiral superstructure. The differential response between right and left polarized light is not only used as a diagnostic but may also provide a means to convert light’s spin angular momentum into chiral excitonic states, which in turn may have different transport, charge-separation rates or intermolecular interactions.^255,256 However, the system must display sufficient order to retard the dephasing of the angular momentum states.²⁵⁷

Orbital Angular Momentum

Photon packets can be described by quantum numbers that indicate their intrinsic spin angular momentum (SpAM), their number states, their energy, and their transverse spatial mode. For spin and transverse modes, the light can carry angular momentum, which can interact both classically and quantum mechanically with materials. While SpAM is widely used for quantum information protocols,²⁵⁸ helical transverse chirality (OAM) is not commonly used to transmit nor to encode additional information in the photons emitted from a material.²⁵⁹

Similar to SpAM, OAM modes carry quantized angular momentum in proportion to the electric field phase difference around a centrosymmetric position. Thus, OAM can carry quantum information through pure, superposition, and entangled states.²⁶⁰ One exciting potential application of OAM is the ability to drive transitions beyond the dipole limit.²⁶¹ Many qubit transitions are defined within a quadrupolar or magnetic dipole subspace, and such transitions can only be driven by electric field gradients, carried in the OAM field. Improving the fidelity of OAM quantum information transfer may require near-field OAM photonics, in the visible and microwave regions.^262,263

Recently, researchers have found that OAM can induce specific quantized transitions in atomic ions,²⁶⁴ highly bound Rydberg excitons in semiconductors,²⁶⁵ and possibly also in nondegenerate valley states of 2D materials.²⁶⁶ These experiments demonstrate the potential for helical OAM to drive states amenable for use in quantum information systems, and given the latter two cases, extended chiral excitons may be the key to unlocking the potential of chiral transverse modes in information transduction.

The effect of OAM dichroism in isotropic matter has been theoretically predicted by Afanasev et al.(267) With this additional degree of freedom, the definition of dichroism becomes somewhat ambiguous. For instance, Kerber and collaborators in their paper on OAM-light interacting with nanoantennas²⁶⁸ point out that even for the case of fixed, yet nonzero OAM, one gets six distinctive types of dichroic effects. As a convenient solution to this branching problem, they presented the following probe classification: (1) parallel class beams with |OAM, SpAM⟩ = |↑↑⟩ and (2) antiparallel class beams |OAM, SpAM⟩ = |↑↓⟩. The importance of this classification was recognized earlier in the realm of OAM light interacting with nano-objects²⁶⁹ and atomic matter.²⁷⁰ This framework can be adopted straightforwardly in other subfields of twisted light and matter studies, for example, studies that employ electron, proton, and neutron beams as probes of matter.

Violation of spin selection rules due to photon-atom OAM transfer was observed experimentally in photoexcited trapped ions. Based on these discoveries, the effect of local CD was predicted at the level of multipolar contributions to an atomic photoabsorption amplitude.²⁷¹ It was concluded that OAM light of different helicities does not couple symmetrically to atoms with high-order multipolar content, reflecting on the earlier findings. The phenomenon is impact parameter dependent and becomes stronger near the beam axis.

Further Strategies for Enhancing Light–Matter Interactions

From the field of nano-optics and nanoelectronics, a variety of techniques are capable of enhancing the probe-matter interactions strengths. Turning to the former, light–matter interaction enhancements leverage a number of techniques developed over the last two decades including polaritonic optical modes such as surface plasmon polaritons.¹⁵⁴ However, given the high optical losses due to free carriers in metals, hybrid photon–plasmon optical modes were introduced.²⁷² These hybrid modes will become important in the context of weak optical signals and possible in the limit of single quanta for information processing. Demonstrated in integrated photonics, such hybridized optical modes yield functional and high-performance devices including electro-absorption modulators^273,274 and plasmon laser sources.²⁷⁵ Another possibility of enhancing light–matter interactions is to use the strong exciton binding energy of low-dimensional materials, such as those from the family of TMDs which have binding energies in the range of hundreds of meV,^276,277 exciton–polariton lattices,²⁷⁸ or chiral field detection,²⁷⁹ toward the goal of room-temperature condensates,²⁸⁰ and quantum technologies.

In general, enhancing light–matter interactions can be achieved by increasing the interaction time and matching wave functions of light and matter. Regarding the former, effects that increase the interaction time of the electromagnetic field with matter include slow-light effects as well as resonant effects. The latter splits into optical resonances such as engineered by optical cavities, on one hand, and into material resonances such as simple two-level systems or polaritonic transitions on the other. All of the above shall be also explored in the context of chiral coherent transduction in future research. The class of slow-light techniques rely on raising the group index and includes, waveguide mode dispersion engineering,²⁸¹ or coupled cavities.²⁸² Another slow-light effect, that, interestingly, does not rely on traveling waves, is the effect of epsilon-near-zero (ENZ);^283,284 such enhanced interactions are enabled by the presence of the optical nonlinearity (Δn) scaling as ϵ^–1/2. Thus, as the real part of the permittivity approaches zero, the optical nonlinearity diverges. Physically, as the optical field is slowed down, its energy is stored inside the electrical field strength. This is exciting for nano-optics, since it allows for strong light–matter interaction effects at nanometer or tens of nanometer dimensions. These ENZ effects have been used, for instance, in ITO hybrid plasmon optical modes, to demonstrate efficient electro-optic modulators.²⁷³ Second, light–matter interactions can be enhanced via impedance matching, where the electromagnetic field, typically 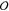(10³ nm) for visible to near-infrared frequencies, is matched to the length scales of electronic wave functions of matter (electronic systems), which are 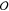(10⁰ nm). This mismatch of 3 orders of magnitude is the origin of the weak interactions of electromagnetic waves with matter. Dispersive effects such as the aforementioned polariton modes allow for high k-vector shrinking of the effective wavelength, and thus facilitating increased light–matter interactions.

Leveraging Chirality in the Quantum Sciences

A scientific revolution enabled by quantum information processing is underway. Successful quantum computing hardware will depend both on incremental technological improvements and on disruptive applications of physical laws underpinning how qubits read, store, and transduce information. The challenge addressed here is to rethink quantum information protocols to incorporate chiral “handles”, as described in the preceding sections on enantioselective spin-dependent effects. That is, can nanoscale chirality be leveraged to create innovative approaches to quantum information processing (QIP)?

Exploiting chirality as a design framework for quantum devices will enable the control of spin, charge, and energy transport using molecules and interfaces so that quantum information can be preserved and transferred at room temperature. A key concept is the manipulation of the magnetic response in chiral molecules and engineered nanomaterials via CISS. This approach includes controlling spin filtering and polarization capabilities of molecules and engineered nanomaterials and generating qubits through molecular design, surface architectures, and tailored interactions with light with chiral degrees of freedom. A complementary focus is the study of quantum transduction processes at soft–hard materials interfaces, involving the transfer of both spin polarization from electrons to nuclei and field-mediated chirality transfer. Next, we draw from the rapidly advancing and diverse areas of research on chiral systems described above (1) to explore potential experimental approaches to coherence in charge and spin transfer in chiral molecules, (2) to highlight the most promising avenues to implement chiral molecular, crystalline, and nanostructured materials for QIP, and (3) to discuss where chirality may play a role in hypothesized nontrivial quantum effects in biological systems.

Measuring Coherence in Charge and Spin Transport

Measuring spatial and spin coherences in electron transport through chiral systems will be crucial to answering the two main questions posed in the introduction in the context of chirality: (1) What transduction efficiencies are possible? (2) To what extent can coherence be preserved both during the transduction and also while propagating once induced?

Break-junction measurements in STM provide nano- structured, mobile electrodes to make contact with single molecules and to study charge transport properties.^285−288 This approach can be used to distinguish incoherent hopping from coherent tunneling transport regimes. Two electrodes are brought into and out of contact with molecules of interest, and when the two electrodes are withdrawn, the current is measured. When a molecule binds between the two electrodes, a plateau is observed in the current vs distance trace. By measuring thousands of these traces, it is possible to determine statistically the conductance of a single-molecule junction. These systems have been used extensively to study charge transport in chiral molecules such as DNA,^289−293 RNA,^294,295 peptide nucleic acid,²⁹⁶ peptides,^297,298 and proteins^299,300 and were used to explore spin-selectivity in a variety of molecules by either applying a magnetic field or by using spin-polarized electrodes to inject polarized spins.^301,302

Specifically, Aragonès et al. found that conductance between ferromagnetic Ni tips and Au surfaces bridged by sulfur-terminated α-helical peptides (cysteine residues) depends on the tip magnetization direction and handedness (l or d) of amino acid residues,¹⁰⁷ as shown in Figure 23. When a spin-polarized source of electrons is used to inject charge into one of the α-helical barrel isomers (l or d), the conductance values are observed to depend consistently on both the orientation of the spin injected and handedness of the chiral helical peptide during the charge transport measurement. The spin polarization power of a single peptide strand can then be calculated by the conductance relation (Gl/d ↑ – Gl/d ↓)/(Gl/d ↑ + Gl/d ↓), where Gl/d is the conductance of either the l- or d-isomer and the arrows indicate the orientation of the injected electron spin. Exceedingly high spin polarization powers scoring 60% are registered for a single α-helical peptide barrel of 22 amino acids (∼3 nm long). The results highlight a direct correlation between electron spin polarization and transport. Still, additional experiments are needed to distinguish unambiguously incoherent hopping from coherent tunneling in spin-dependent conductance through chiral molecules. Moving forward, systematic investigations of the influence of monomer sequence, length, and molecular dipole on conductance using spin-polarized STM-BJ techniques could be used to answer these questions and to explore spin filtering that arises from the CISS effect.³⁰³

Figure 23.

Conductance histograms for hundreds of single-peptide junctions collected in different scanning tunneling microscopy break junction experiments with Ni tips magnetized (a) down and (b) up for both left- and right-handed α-helical peptides. These peptides are composed of 22 amino acid residues bridges attached to gold substrates. Insets depict representative current vs pulling traces with well-defined single-molecule plateau features. Conductance values were extracted from Gaussian fits to the histograms. Adapted with permission from ref (107). Copyright 2017 John Wiley and Sons.

Measuring spin coherence in ET, transport, and transmission is also critical to advance our understanding of CISS. Kumar et al. showed that when injecting spin-polarized electrons from chiral molecules into an AlGaN/GaN device hosting a 2D electron gas layer, spin coherence lifetimes on the order of 10 ms or more at room temperature could be detected in the semiconductor.³⁰⁴ However, understanding spin dynamics inside the molecules themselves remains lacking. Determining the ET dynamics of covalently linked donor–chiral spacer–acceptor (D−χ–A) molecules following photoexcitation is an ideal model system to understand the CISS effect on the coherent spin dynamics of radical pairs produced in these systems. Moreover, such radical-based molecular systems are significant for their potential use as molecular qubits. The ET efficiencies in covalent (D−χ–A) systems depend on competing photophysical processes, some of which operate on subnanosecond time scales (Figure 24a).³⁰⁵ Typically, femtosecond and nanosecond transient absorption spectroscopies are used to characterize the ultrafast ET dynamics of (D−χ–A) molecules used to probe the CISS effect. In addition, these techniques provide the electronic spectra of the intermediates that produce (D^•+–χ–A^•–), for example, (D^•+–χ^•––A), as well as the spectra of (D^•+–χ–A^•–) itself. The CISS effect is expected to alter the ET dynamics, so that determining the ET dynamics at all relevant time scales is critical.³⁰⁶

Figure 24.

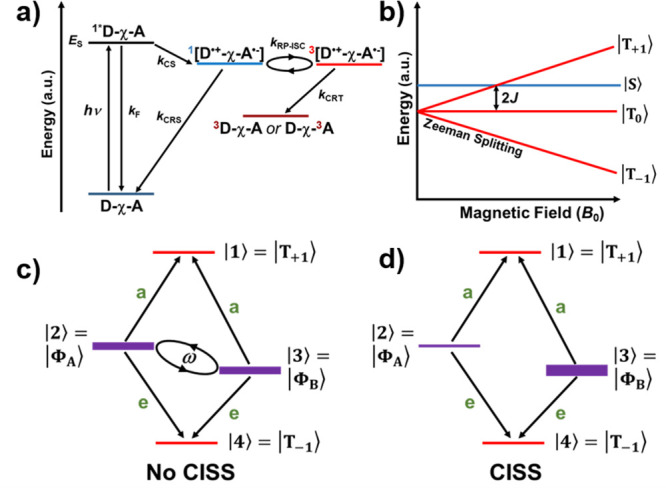
(a) Electron transfer and intersystem crossing pathways in a (D−χ–A) system, where k_CS is the charge separation rate constant, k_RP-ISC is the radical pair intersystem crossing rate constant, and k_CRS and k_CRT are the charge recombination rates via the singlet and triplet channels, respectively. (b) (D^•+–χ–A^•–) energy levels as a function of magnetic field for 2J > 0, D = 0. (c) (D^•+–χ–A^•–) energy levels in the high field limit with no CISS, where ω is the mixing frequency and the enhanced absorptive (a) and emissive (e) microwave-induced transitions are indicated. (d) (D^•+–χ–A^•–) energy levels with chiral-induced spin selectivity in which only |3⟩ is populated.

Figure 24a shows the Jabłoński diagram of the photophysics involved in (D^•+–χ–A^•–) generation from the photoexcited singlet state of D or A having energy E_S. If (^1*D−χ–A) → (D^•+–χ–A^•–) occurs in ⩽1 ns, a quantum-entangled electron spin pair initially in a singlet state is formed, which has been studied in systems ranging from photosynthetic proteins^307−312 and related model systems^{305,313−315} to DNA hairpins, and is commonly referred to as a spin-correlated radical pair (SCRP).^316−320 When (D^•+–χ–A^•–) distances are ⩾15 Å, the g-factors and hyperfine interactions (a) of D^•+ and A^•– are usually on the same order of magnitude as their spin–spin exchange (J) and dipolar (D) interactions, resulting in coherent spin evolution that mixes the singlet and triplet (D^•+–χ–A^•–) states.^{307−309,321−326} Moreover, if (D^•+–χ–A^•–) is produced in a magnetic field that is large relative to J and D, Zeeman splitting of |T₊₁⟩ and |T_–1⟩ away from |T₀⟩ results in exclusive coherent mixing of the |S⟩ and |T₀⟩ states of (D^•+–χ–A^•–) to give |Φ_A⟩ and |Φ_B⟩, which are initially populated (Figure 24b).³²⁷ Since |Φ_A⟩ and |Φ_B⟩ have triplet character, four allowed transitions occur between them and the initially unpopulated |T₊₁⟩ and |T_–1⟩ giving rise to spin-polarized electron paramagnetic resonance (EPR) spectrum signals (Figure 24c). If charge transfer occurs through a chiral spacer, such as in (D−χ–A), the spacer induces a spin polarization that depends on the chirality and the direction of the ET. As a result, only one of the four two-spin states is populated in the weak coupling limit, with vanishing entanglement between the hole and electron spin (Figure 24d).³²⁸ Moreover, CISS reduces the efficiency of the charge recombination reaction as well.³⁰⁶

Other experiments were recently proposed that use such magnetic resonance techniques to detect spin coherence and signatures of electron spin polarization in molecular (D−χ–A) systems. Fay introduced the possibility that CISS could lead to quantum coherence between spin states rather than spin polarization with different phases of initial coherence depending on the chirality.³²⁹ This coherence could have an impact on understanding reactions involving radicals and radical pair formation as well as other chiral open-shell molecular processes. To test this hypothesis, an EPR experiment was posited that uses out-of-phase electron spin–echo envelope modulation (OOP-ESEEM) to detect phase shifts in measurable signals based on realistic parameters (Figure 25a,b). Chiesa et al. proposed a series of magnetic resonance experiments to search for unambiguous acceptor polarization following photoexcitation of a donor and charge transfer through a chiral bridge (Figure 25c,d).³³⁰ A qubit could be used as a local, highly sensitive, and coherent magnetic sensor of polarization transfer in time-resolved EPR measurements, ideally, without influencing the underlying ET process. Alternatively, the qubit state could be monitored following coherent transfer of polarization from an acceptor to the qubit, which can be accomplished using appropriate microwave pulse sequences.

Figure 25.

(a) Schematic of radical pair formation in donor–bridge–acceptor species and pulse sequence in a hypothetical out-of-phase electron spin–echo envelope modulation (OOP-ESEEM) electron paramagnetic resonance (EPR) experiment. (b) Calculated OOP-ESEEM signal from opposite enantiomers in a chiral radical pairs showing different phase shifts. Panels (a,b) adapted with permission from ref (329). Copyright 2021 American Chemical Society. (c) Proposed EPR and (d) Nuclear magnetic resonance (NMR) experiments to elucidate the role of chiral linkers in spin-dependent transfer in chiral donor–bridge–acceptor pairs. Panels (c,d) adapted with permission from ref (330). Copyright 2021 American Chemical Society.

A (D−χ–A) system that can be used to study the CISS effect on biological ET using SCRPs could use helical DNA as a probe. Wasielewski and co-workers have recently studied DNA hairpins in which ultrafast photoinduced ET produces SCRPs.^316−320 The SCRPs within DNA hairpins have been prepared by selective photoexcitation of different chromophores incorporated as the hairpin linker that joins the two single strands of DNA, as substituents at abasic sites within the hairpin, or as capping groups appended to the end of the duplex.^316−320 Photogenerated SCRPs were prepared within chromophore-modified DNA hairpins with varying SCRP distances and probed using time-resolved EPR spectroscopy with continuous (TREPR) and pulse microwave irradiation (pulse-EPR). For example, Figure 26a shows the TREPR spectrum of the NDI^•––Sd^•+ SCRP prepared by selective laser photoexcitation of the hairpin linker NDI followed by subpicosecond hole transfer to an adjacent adenine nucleobase, hole transport through the adenine and guanine bases, and trapping at the Sd donor.

Figure 26.

(a) Time-resolved electron paramagnetic resonance spectrum of NDI–A₃G₁–Sd at 85 K, 100 ns after a 355 nm, 7 ns laser pulse (black trace) and its simulation (red trace). (b) Out-of-phase electron spin–echo envelope modulation (OOP-ESEEM) for NDI–A₂G_n–Sd hairpins. Experimental data are shown for NDI–A₂G₂–Sd (red), NDI–A₂G₃–Sd (blue), and NDI–A₂G₄–Sd (green). Simulated echo modulations (black) used to predict the SCRP distances listed for each hairpin based on the extracted dipolar coupling constant. (c) Cartoon of NDI–A₂G₂–Sd illustrating the rotation of the Sd end-cap necessary to achieve the measured radical pair distances between NDI^•– and Sd^•+. All panels adapted with permission from ref (318). Copyright 2019 American Chemical Society.

Pulse-EPR techniques have been used to obtain detailed information about J and D for photogenerated SCRPs in DNA hairpins, where D gives detailed distance and structural information as well as providing a direct probe of spin coherence in the SCRP. For example, if photogeneration of the SCRP is followed by a microwave pulse Hahn echo sequence, π/2−τ–π–τ–echo, and the time delay τ is scanned, coherent oscillations between |Φ_A⟩ and |Φ_B⟩ that are related to both J and D result in oscillatory modulation of the spin–echo amplitude.^{312,321,331−334} When this experiment is performed on spin-coherent SCRPs, the echo appears “out-of-phase,” that is, in the detection channel in quadrature to the one in which it is expected and is therefore termed out-of-phase electron spin–echo envelope modulation (OOP-ESEEM).^{312,321,331−334} If J is small, the OOP-ESEEM oscillation frequency is approximately 2D/3. Since D ∝ 1/r_DA³, where r_DA is the SCRP distance, OOP-ESEEM can be used to measure SCRP distances.^{318,333−335} Most importantly in this context, the observation of strong OOP-ESEEM shows that spin coherence is maintained in the SCRP.^312,331,332 Recent theory has shown that based on the phase relationships of these coherent oscillations, OOP-ESEEM can be used to detect the CISS effect on the spin coherence of SCRPs.^329,330,336Figure 24b shows coherent OOP-ESEEM oscillations in a DNA hairpin that result primarily from D. In addition, By performing pulse-EPR measurements on related DNA hairpins, selective probing of each spin comprising the SCRPs has also demonstrated coherence times of more than 4 μs,³³⁷ which provides a comfortable time window for performing the spin manipulations suggested by theory as necessary to determine the extent of the CISS effect on their spin dynamics.^329,330,336 In order to observe the CISS effect on the spin dynamics of SCRPs, it will be necessary to prepare DNA helices having opposite chiralities.

Elucidating the roles that coherence and dephasing effects play on the CISS effect in biology and how they may be leveraged for quantum information processing would provide a significant leap in our understanding. These emerging areas of research into chirality and spin effects will benefit from parallel advances in quantum sensing using, for instance, NV centers in diamond, and other color centers for probing and readout of coherent superpositions in single- and many-spin systems.

Chirality Control of Superconducting Interfaces

Spin-selective transport through chiral molecules shows unusual conduction phenomena near superconducting interfaces. In particular, chiral α-helical polyalanine molecules that are in proximity to niobium superconductors (through chemisorption on metallic layers) show unconventional superconductivity. Shapira et al. used scanning tunneling spectroscopy (STS) to analyze a multilayered polyalanine-gold bilayer-niobium substrate and found zero-bias conductance peaks embedded in a bandgap from the tunneling spectra.³³⁸ This zero-bias peak is reduced in the presence of a magnetic field but does not split, indicating an unconventional order parameter that is consistent with equal-spin triplet pairing p-wave symmetry. In comparison, the adsorption of nonhelical chiral cysteine molecules showed no change in the order parameter.

Junctions of superconducting niobium and metallic films bridged by chiral α-helical polyaniline induced p-wave order-parameters, demonstrating phase-coherent transport through chiral organic films.³⁴⁰ Alpern et al. analyzed proximity effects of chiral films in multilayered superconducting systems and found that chemically adsorbed α-helical polyalanine can induce magnetic-like state behavior. Specifically, in-gap states were found that were nearly symmetrical around a zero-conduction bias that closely resembled Yu–Shiba–Rusinov states,³³⁹ see Figure 27. Collectively, the observations described above provide evidence that chiral molecules can behave as magnetic impurities when in proximity to superconductors, enabling a wide range of potential applications for spin-selective transport through superconducting films.

Figure 27.

Conductance properties of a low-resistance (120 Ω) NbSe₂/Au junction after chemisorption of chiral molecules on the NbSe₂ flake (∼25 nm thick). (a) Temperature dependence of dI/dVvsV spectra showing a distinct zero-bias conductance peak (ZBCP) that vanishes at higher temperatures (but still below T_c). Inset: Illustration of a chiral-molecules/NbSe₂-flake/Au sample. (b) Temperature dependence of the conductance at zero bias with two transition temperatures marked by arrows: T_c = 7.2 K, where the zero bias conductance starts to rise due to the Andreev dome and 5.5 K where a zero bias conductance peak starts to appear. Inset: Optical image of the sample with the measurement scheme depicted. (c,d) Perpendicular (c) and parallel (d) magnetic field dependencies of the conductance spectrum, showing that in high magnetic fields, yet below the parallel and perpendicular critical fields (H_c2) of bulk NbSe₂, the zero-bias conductance peak vanishes, revealing an underlying gap. All panels adapted with permission from ref (339). Copyright 2019 American Chemical Society.

Spin Superradiance and CISS

Cooperative effects are associated with the system as a whole, and not with its individual components in isolation. These phenomena occur at every scale, ranging from atoms in crystals producing ferromagnetism, excited states producing superradiance (SR), superconductivity, functionality in complex molecules, and the emergence of life from biomolecules.³⁴¹ One of the most interesting properties of some cooperative effects is their robustness to noise induced by the external environment. For this reason, cooperative effects could play essential roles in the successful development of scalable quantum devices that operate at room temperature.

Superconductivity is a well-known cooperative quantum effect, but others, such as SR, are also robust to noise.^342,343 Superradiance, proposed by Dicke in 1954,³⁴⁴ arises from the excitation of an ensemble of individual systems and results in an emissive, macroscopic quantum state. Superradiant emission is characterized by an accelerated radiative decay time, where the exponential decay time of spontaneous emission from the uncoupled two-level system is shortened by the number of coupled emitters. In addition, when the excitation is incoherent,³⁴⁵ SR exhibits a delay or build-up time during which the emitters couple and phase-synchronize to each other. This time corresponds to the time delay between the excitation and onset of the cooperative emission. In the case of SR, the coupling of an ensemble of emitters to an external field can induce an energy gap, making superradiant states robust to disorder. Interestingly, the superradiant energy gap, in certain limiting cases, is the same magnitude as the superconducting gap.³⁴⁶

Superradiance has been observed in a wide range of systems,³⁴⁷ including cold atomic clouds,³⁴⁸ photosynthetic antenna complexes,³⁴⁹ molecular aggregates,^350,351 QDs,^352,353 NV centers in nanodiamonds,³⁵⁴ and lead–halide perovskite nanocrystal superlattices.³⁵⁵ This effect is relevant to enhancing absorption and energy transfer, which was proposed to improve the efficiency of light-harvesting systems and photon sensors.^356−360 Superradiance also leads to spectrally ultranarrow laser beams.³⁶¹

Although the vast majority of systems exhibiting SR involve electronic transitions at optical frequencies, SR has also been observed in spin systems.³⁶² Spin SR has attracted much attention due to its many possible applications to sensing and spin masers (microwave amplification by stimulated emission of radiation).^363−366 Measuring the delay time of a superradiant burst provides an accurate evaluation of the triggering intensity because the delay time depends exponentially on the intensity of the external pulse and spin SR can be triggered by extremely weak external pulses. Thus, systems exhibiting spin SR can be used to produce sensitive detectors. Another interesting application of spin SR is spin masers.^367−369 A superradiant spin system is a source of coherent radiation at radio frequencies between 0.3 and 300 GHz, wavelengths between 1 m and 1 mm, respectively, and can act as the microwave analogue of the laser. There are important applications for masers in ultrasensitive magnetic resonance spectroscopy, astronomical observation, space communication, radar, and high-precision clocks.

The key to spin SR is the population inversion of the emitters. In spin systems, population inversion corresponds to spin polarization, which is a required condition for SR emission and maser operation when a polarized spin population is present in a microwave resonator cavity. For this reason, it would be intriguing to exploit the CISS effect^53,91 in connection with spin SR and spin masers. Indeed, the spin-polarized beam emerging from chiral molecules due to the CISS effect could be used to induce an SR pulse. A beam of polarized electron spins could also be used to operate a spin maser when coupled to a microwave resonator cavity. Moreover, it is known that a polarized electron beam couples with nuclear spins by hyperfine spin–spin interactions. This coupling would produce a shift of the nuclear magnetic resonance frequency of nuclear spins and would thus enhance the coupling between the nuclear spins and the resonator. These effects could be used both to study the CISS effect and to build more efficient SR or maser nuclear spin systems.

Spin Polarization and Entanglement in Hybrid Quantum Dot Systems

A recent study found that the CISS effect vanishes when all electron states with the same energy are equally likely, a consequence of the Onsager reciprocal principle.⁴² The generality of this result means that the CISS effect needs to be understood in terms of the specific experimental settings. Three possible situations have been suggested:⁴² (1) the electronic states with the same energy not being equally probable (e.g., for electrons generated optically by a laser, due to selection rules inherent in photoexcitation processes), (2) the presence of accidental degeneracy in the molecular spectrum, which enhances the SOC, or (3) the presence of a magnetic lead. More recently, analyses based on symmetry in electronic transmission were carried out to understand the origin of the CISS effect.⁵³

While strengthening the SOC by coupling a chiral molecule to a heavy metal or to a superconductor can enhance spin polarization, control and manipulation are difficult. A potential approach is to exploit a hybrid structure that couples a chiral molecule to a 2D QD to form a “super chiral molecule” to control and manipulate spin polarization, as illustrated schematically in Figure 28. The idea originates from recent studies to control spin polarization by exploiting classical chaotic dynamics^370,371 and spin Fano resonances.³⁷²

Figure 28.

A schematic illustration of a “super chiral molecule”: a coupled chiral-molecule/quantum dot (QD) hybrid structure, for controlling and manipulating spin polarization and entanglement. The gate voltage is applied to change the QD structure for controlling spin polarization.

The role of classical dynamics in spin transport is intriguing from the point of view of a classical-quantum correspondence, as spin is a purely relativistic quantum mechanical variable. Nevertheless, due to SOC and because the orbital motion does have a classical analogue, the nature of classical dynamics can influence spin. Full quantum calculations and a semiclassical theory revealed that spin polarization can be modulated effectively if the geometrical shape of a QD can be modified to produce characteristically distinct classical behaviors ranging from integrable dynamics to chaos.³⁷² Chaos can play distinctive roles in affecting spin polarization, depending on the relative strength of the SOC. For weak couplings with characteristic interaction lengths much larger than the system size, chaos can preserve and even enhance spin polarization. In the strong coupling regime, where the interaction length is smaller than the system dimensions, chaos typically degrades or even destroys spin polarization. In 2D materials, such as graphene, a QD can be realized by applying a properly designed gate potential. The total spin polarization from the hybrid structure can then be manipulated electrically.

In electron transport through mesoscopic systems, the various resonances associated with physical quantities, such as conductance and scattering cross sections, are characterized by the universal Fano formula.³⁷³ Recently, a Fano formula was discovered to characterize the resonances associated with two fundamental quantities underlying spin transport: the spin-resolved transmission and the spin polarization vector.³⁷² A Green’s function formalism was generalized to describe spin transport and the Fisher-Lee relation was used to compute the spin-resolved transmission matrix, enabling the spin polarization vector to be calculated and leading to a universal Fano formula for spin resonances. The resonance width depends on the nature of the classical dynamics, as defined by the geometric shape of the dot, and this property could be exploited for control. Since characteristically distinct types of classical dynamics including chaos can be readily generated in the QD through geometric deformations,³⁷⁴ Fano spin resonances can be modulated accordingly. This work provides a theoretical foundation for the general principle of controlling spin polarization in the chiral molecular system through manipulating the classical dynamics in the QD, which can be experimentally realized by applying a properly designed local gate potential profile. Likewise, modulating the classical dynamics in a different way can enhance the spin Fano resonance. The control principle was computationally demonstrated in a key component in spintronics: a class of nanoelectronic switches, where the spin orientation of the electrons associated with the output current can be controlled through weakening or enhancing a Fano resonance.³⁷²

Quantum Information Storage and Transduction

We believe it is timely to begin to exploit the distinctive properties of chiral molecules and chiral material interfaces to develop room-temperature device technologies for quantum sensing, quantum storage, and quantum computing. Tailoring OAM couplings by acting either on the spin quantum states (that serve as qubits) and/or on the interaction potentials could enable room-temperature transduction of quantum information.

Quantum information processing and quantum sensing have made enormous strides in the recent past. Superconducting circuits and ion traps have led to a race for supremacy in quantum computing, while ultracold atoms and molecules, NV, and other color centers have enabled a variety of approaches to quantum sensing (e.g., magnetometry, dark-matter detection, atomic clocks). With the exceptions of NV centers and atomic vapors, experiments require extremely low temperatures (mK range) to protect the coherent states and to allow sufficient time for entanglement to evolve and/or for measurements to be made. This constraint restricts their use to systems with sizable infrastructure support. The main drawbacks of qubits based on defect centers at present are the difficulties of fabricating them at specific locations,^375−377 selectively addressing different centers, and establishing quantum information transfer beyond the short dipole–dipole interaction length scales.

In contrast to the approaches described above, chemical syntheses of chiral materials afford the opportunity to build quantum information systems from the bottom up, taking full advantage of the quantum properties of matter on the atomic scale. Chiral molecular systems differ from current qubit implementations described above in three important ways. First, chemical synthesis enables control over the nature of the qubit itself, thus enabling careful tuning of individual quantum states. Second, covalent and noncovalent interactions between molecules can be used to construct atomically precise arrays of qubits. This approach offers the possibility of controlling and interrogating the properties of a qubit both in isolation and as part of an array, providing insights into the quantum properties of multiqubit arrays. Third, chiral molecules have the potential to serve as long-range quantum information transducers.

It may be possible to transfer chiral spin information between electrons and nuclei via hyperfine interactions. Spin-polarized electrons can be generated on the surfaces of topological insulators (TIs) through the application of electrical current.³⁷⁸ The coupling of the electron spin to the nuclear spin via hyperfine interactions highlights the ability to produce dynamic nuclear polarization.^378,379 A promising application is a rechargeable spin battery.³⁷⁸ These recent results point to two applications: (1) TIs can be used to generate spin-polarized electrons, which can interact with nearby chiral molecules and biomolecular structures through highly reproducible, high-precision contacts; and (2) interactions with radical pair states are also possible, particularly in the context of the repair of lesions in duplex DNA, where the repair yield is dependent on the strength and angle of the applied magnetic field.²⁷ Chiral spin modes on the surface of a TI can be used as an additional degree of freedom for manipulating the polarization.³⁸⁰

Chiral molecules could also be harnessed for quantum information transduction. Nanochiral materials could be used as quantum wires connecting a node of quantum sensors. For example, we envision testing chiral materials as tractable, in-chip solid-state quantum wires connecting established quantum sensors (e.g., color centers in diamond, silicon, or silicon carbide), see Figure 29. Proposals for connectivity among quantum sensors have traditionally relied on dipole-coupled spin buses,³⁸¹ which unfavorably limit the maximal distance between nodes, and which can hardly be engineered. Conversely, quantum information transduction through chiral materials will overcome both of these limitations, and the chiral materials have already been shown to be capable of quantum information transduction and topological-like transport over longer distances and in complex environments.²⁰

Figure 29.

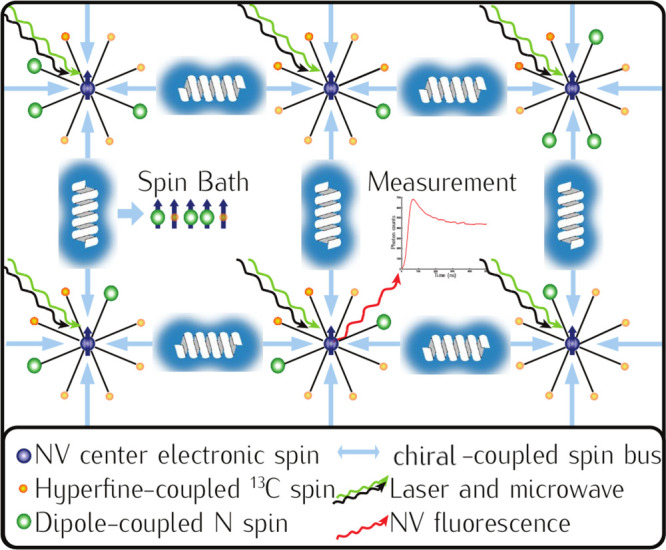
Chiral molecules could be used as interconnects or quantum information transducers that have a longer-range than dipolar-coupled spin buses.

Decoherence and Entanglement Considerations

The realization of devices for near-room-temperature, CISS-based quantum information processing will necessitate deeper understanding of interactions with the decohering bath. Investigation of single-qubit coherence properties under controlled noise (electron–electron, electron–phonon scattering) environments will be needed to inform the design of chiral materials and devices for quantum information processing. For example, spin textures are complex results of electronic correlations.³⁸² If electron–electron interactions can be effectively decoupled, CISS can still be sustained by the material, since it results essentially from the SOC and breaking inversion symmetry under ET, transport, or polarization conditions. Understanding the bath dynamics and the application of reservoir engineering principles can be achieved with proof-of-principle experiments relying on controlled charge injection into nanochiral materials, combined with quantum information/sensing protocols for spin-state preparation, control, and readout.

Another key issue is entanglement. For a quantum system with multiple degrees of freedom, loss of coherence in a certain subspace is intimately related to the enhancement of entanglement between this subspace and another one. It would be useful to investigate intraparticle entanglement between spin and orbital degrees of freedom in the chiral molecular system with different types of classical dynamics in the QD. Of particular interest is the spin degree of freedom in the weak SOC regime where, as existing studies suggested, it is possible to use classical chaos to enhance SO entanglement significantly at the expense of spin coherence.^370−372

Control of Light–Matter Interactions

Taken together, the combination of both the orbital and spin angular momenta of light as well as coupling dictated by the direction of light propagation and polarization of single photon emitters provide exciting avenues for quantum control.³ Importantly, the recent advancements in design, optimization, and fabrication of plasmonic and nanophotonic architectures capable of strong spatiotemporal confinement of light provide possibilities for chiral quantum optics, where modulating or maintaining phase, polarization, and intensity is critical, often with directional emission. Accurate descriptions of the dynamics of these systems will need to address the quantum nature of light, of electrons, and of coupled molecular states and not focus solely on either the condensed matter system or quantization of electromagnetic fields while oversimplifying the other. This significant theoretical challenge must be overcome when investigating combined electron transport properties and optical confinement at the nanoscale.

Additionally, a critical challenge for using OAM for quantum control is to enforce the interactions of the emitter with the inhomogeneous spatial mode of the electromagnetic field, which are addressed by the following two questions: (1) How can one design materials that interact strongly with OAM fields via extended excitonic states? Many delocalized systems already couple strongly to spin angular momentum through either macroscopic helicity (e.g., helical molecular aggregates) or through degenerate points in their band structure (e.g., valleytronic 2D materials), but spin angular momentum combined with OAM remains experimentally underexplored. It needs to be established how mesoscopic helicity in designed and self-assembled materials can control and enhance interactions with OAM fields. (2) How can one implement subwavelength optical fields with OAM that will strongly interact with matter? Near-field photonics can create field gradients that are far stronger than the free-space modes (thus preventing decoherence) and that can be used to drive high-order transitions (such as electric quadrupole) far more efficiently than the vacuum (i.e., spontaneous emission). Controlling quantum information via spatially engineered electromagnetic fields that provide environmental control of angular momentum would be transformative for quantum-enabled technologies.

Let us consider light–matter interactions akin to deformations in chiral molecules induced by mechanical means such as applying an external force. These deformations are nontrivial due to the nonuniform distribution of the load depending on the molecule structure. A model by de Gennes³⁸³ predicted that DNA externally pulled by mechanical means deforms only close to the mechanical contacts, leaving the bulk of the molecule undeformed. Such a stretching process is thus hampered by details of the contact. An alternative to pulling on the molecule is to shine light on it at low intensity and at an appropriate frequency to modulate the strength of the electronic bonding in the molecule and thus changing its rigidity at a fixed external force so that it stretches or compresses in particular ways in the bulk structure. This approach is also known as stretch engineering. In addition, the role of symmetries in the CISS effect has recently been considered in ref (384), where the authors present a model that consists of two interconnected tight-binding chains, mimicking two interacting helices, including SOI and attached to two Fermionic reservoirs playing the role of current terminals. It is noteworthy that SOC is particularly sensitive to such mechanical changes being dependent on the detailed relative geometry of the spin-active units.^111,385 Indeed, deformation-dependent spin activity has been shown experimentally^386,387 and has been modeled analytically in DNA¹³⁷ and in oligopeptides,³⁸⁸ where the roles of hydrogen bonding during stretching or compression have been addressed.

A natural extension of the previously considered works is to model the nonequilibrium spin response induced by the interplay of both SO interactions and light–matter coupling in these chiral systems (Figure 30). The natural formalism for dealing with periodically driven interactions is the so-called Floquet theory,³⁸⁹ analogous to the Bloch theory for spatially periodic interactions. Within this context, considering the coupling of charge carriers in the chiral sample to monochromatic radiation fields could provide another means to address the spin degree of freedom, offering additional tunability to the CISS effect. The use of the Floquet formalism in the description of laser-assisted transport in molecular junctions has been discussed.³⁹⁰

Figure 30.

Effects of light on chiral molecules through the Floquet approach to achieve stretch and spectral engineering. (a) Molecules can be made to stretch or contract by impinging light (b) modulating the spin-orbit coupling. (c) Spectrum normalized by base pair to base pair overlap strength as a function of spin state (s), transport direction (ν) and pseudospin quantum (σ) vs the normalized frequency (ξ) of impinging light. Adapted with permission under a Creative Commons CC BY-NC 4.0 License from ref (137). Copyright 2018 Swiss Chemical Society.

From a physical point of view, linearly polarized electromagnetic radiation carries no angular momentum, in contrast to the circularly polarized electromagnetic fields. One can also consider chiral photons, that is, photons carrying OAM.³⁹¹ Consequently, in the presence of linearly polarized radiation fields, the spin degeneracy of the charge carriers can be broken only if Rashba SO interactions are absent. In other words, circularly polarized electromagnetic fields break the spin degeneracy without SO interactions. For the case of linear dispersion, circular polarization is known to open gaps in the quasi energy spectrum at the degeneracy points when compared with linearly polarized electromagnetic fields.³⁹² Moreover, in dealing with the transport regime, one key point to be considered is that the distribution function of the Floquet states needs not to be a Fermi distribution function. The Floquet problem in which the nonequilibrium distribution is taken into account (already in the absence of static external magnetic field) is difficult, and often one resorts to arguments that justify why the nonequilibrium distribution function can be replaced by a quasi-equilibrium (Fermi) distribution. Sometimes, the conditions that justify this replacement are not explicitly stated in the literature.³⁹³ A possible means to model the photoinduced quasi-1D spin transport in the DNA sample could be achieved by using the approach given in ref (394), where the driven Su–Schrieffer–Heeger model of polyacetylene is explored, and it is shown that competing effects among photon assisted processes and the native topology of the undriven system lead to nontrivial Floquet topological insulating phases.³⁹⁵ Additionally, effective Hamiltonians within the so-called off-resonant regime enable a physical description of the spin transport by means of exactly solvable models.^396,397 Thus, within the Floquet formalism, it becomes possible to deal with periodically driven interactions, and consider the effects of radiation on bonds using the formalism of stretch engineering. Other effects seen in low-dimensional systems such as the spin ratchet effect could also be explored.

Quantum Effects in Biology

Chirality plays fundamental roles in biology, ranging across orders of magnitude in scale. Researchers have pondered the origins of this universal handedness from multiple vantage points, including cosmological,³⁹⁸ astronomical,³⁹⁹ astrophysical,^400,401 biomolecular,^29,402−404 violation of parity symmetry,⁴⁰⁵ and quantum field theory.¹⁰⁸ The connections between spontaneous symmetry breaking, chiral effects, and life are intimate, but this nexus has not been broadly understood.

While CISS effects have been observed in proteins that play critical roles in photosynthesis, photoreception, and electron transport chains, in such experiments, spin-dependent charge transport is measured when isolated proteins were deposited on planar substrates and analyzed using spintronic device architectures, conductive scanning probe measurements, electrochemical measurements, or with Hall device architectures. Notably, these experiments do not reflect natural conditions of electron transport, where native structural conformations and dynamics due to local environments, which can strongly affect spin polarization, can be vastly different. If the biological implications of the CISS effect are to be validated, minimally perturbative in vitro experiments are necessary that can track spin polarization and weak magnetic fields generated by chiral molecules within a cell, without the use of external metal electrodes to detect or source spin-polarized electrons, and by avoiding biotic-abiotic spin-interfaces.

Finding model biological systems to investigate enantioselective and spin-dependent effects are a critical next step. Sensitive relationships between the chirality of underlying quantum (charge, spin, exciton, and plasmon) states and biological function abound. Kurian and colleagues have shown that certain chiral enzyme complexes with palindromic symmetry conserve parity,⁴⁰⁴ and their ongoing work suggests that the chirality is essential for the global synchronization of plasmon-like van der Waals fluctuations and for the symmetric recruitment of energy from DNA substrates for the site-specific formation of double-strand breaks. The application of tools from quantum optics to describe biological chromophore lattices has resulted in the recent prediction of ultraviolet SR in certain cytoskeletal filaments,⁴⁰⁶ which exhibit a striking spiral-cylindrical chiral symmetry (Figure 31) that is reflected in the excitonic wave functions distributed over the chromophore network (Figure 32). The relationship between this electronic SR and its spintronic counterpart is an active area of investigation, which may lead to advanced biosensors and diagnostics.

Figure 31.

(a) Tubulin proteins (left, scale bar ∼5 nm) polymerize into microtubules (right, scale bar ∼25 nm). (b) Highly ordered arrays of tryptophan amino acids (left, in blue) absorb ultraviolet radiation collectively with strong transition dipole moments (right, in red, scale bar ∼25 nm). Reproduced with permission under a Creative Commons Attribution 3.0 License from ref (406). Copyright 2019 IOP Publishing Ltd.

Figure 32.

Quantum probability of finding the collective excitonic state on a single tryptophan residue of a microtubule segment is shown for an extended superradiant state (top row) and subradiant state (bottom row) in lateral view (left column) and in cross section (right column). Microtubule segment consists of 100 spirals (>800 nm) with 10,400 tryptophan residues. Reproduced with permission under a Creative Commons Attribution 3.0 License from ref (406). Copyright 2019 by IOP Publishing Ltd.

Furthermore, exploiting the CISS effect to predict, control, and enhance biological responses is a tantalizing possibility. Take, for example, the case of human immunity. T-cells initiate the body’s immune response by interacting, via their T-cell receptors, with major histocompatibility complex (MHC) peptides on antigen-presenting cells that were exposed to pathogens. The MHC molecules are membrane-bound glycoproteins that form unusually stable bound configurations with antigenic peptide ligands (pMHC), displaying them on the cell surface for recognition by T-cells via T-cell receptor (TCR) engagement.⁴⁰⁷ The TCR activation promotes several signaling cascades that ultimately determine cell fate by regulating cytokine production as well as cell survival, proliferation, and differentiation.⁴⁰⁸ Studies have found that spin-polarized states of antigenic peptides may affect the ability of a TCR to recognize different peptides through conformationally induced spin moments, rather than sheer topology-based affinity, a condition that would render the immune recognition process as fundamentally spin-specific.^409,410

Studies by Antipas et al. show that different pMHCs with nearly identical stereochemistries were complexed with the same TCR, resulting in distinctly different quantum chemical behaviors that depended on the peptide’s electron spin density and expressed by the protonation state of the peptide’s N-terminus.⁴⁰⁹ Spin polarization of different peptides can thus be correlated with downstream signal transduction pathways and their activation of biosynthesis at the transcriptional level. Other studies have shown that noncovalent and dispersive interactions between biological molecules are critical to their functions, in which the electronic charge redistribution in chiral molecules is accompanied by spin polarization.^29,411 Studying chirality, spin polarization, and downstream response in pMHC-TCR interactions could improve our understanding of the impact of chiral-quantum effects on the human immune response, and to develop better tools for therapeutic intervention.

Conclusions and Prospects

In this Review, we have introduced the interplay between chirality and quantum phenomena in several contexts. We have discussed the roles of diverse molecules, materials, and systems in which electromagnetic chiral degrees of freedom can be harnessed for spintronics and quantum information applications. When chirality is introduced into measurements, it produces quantifiable effects that are detectable, for instance, in electrochemical or redox reactions and in spin-selective conduction detected by scanning probe or break junction experiments. These effects are described by the CISS effect, which can be thought of as a spin polarization effect in the absence of magnetic fields. Theoretical descriptions of the CISS effect and other related observations have been done using combinations of DFT and tight-binding approaches, but it remains challenging to capture all the various effects involving electrons, spin, symmetry, and geometry especially for nontrivial systems of large numbers of atoms. Some of the most intriguing observations of SO interactions, the CISS effect, and other chiral-quantum phenomena have been in engineered chiral materials. These experiments have included combinations of organic molecules and metal substrates, substrates with heavy elements, 2D materials functionalized with chiral molecules, and hybrid structures of chiral molecules and nanoparticles. Related effects have also been observed in biological structures. Chirality can also be imparted to electromagnetic fields and can be observed in OAM modes, which may have applications in quantum information systems. Throughout all these contexts, the interplay between chirality, quantum effects, and materials grants possibilities for controlling spin, charge, and energy transport for quantum information processing.

Further experimental implementations of chiral matter are expected to include transduction of spin states into and between molecules, nanostructures such as two-level systems delivered by quantum dots, and circuit-based metamaterials. These ideas inspire nanofabrication of multipolar structures with spatial dimensions fitted to achieve nontrivial chiral response in photonics.⁴¹² This research direction also encompasses the magnetic response of optical devices,⁴¹³ such as those in passive integrated photonics or electro-optics.⁴¹⁴ Free-space reconfigurable optical systems such as spatial light modulators used to realize optical coherent Ising machines⁴¹⁵ and digital mirror displays employed in convolutional neural networks⁴¹⁶ are also of great interest.

Moving forward, chiral-enhanced nanoscience will require a multidisciplinary effort combining cutting-edge materials design and characterization with diverse theoretical strategies, with the long-term goal of designing and controlling chiral (qubit) spin states that operate at room temperature. Some of the crucial developments that will be needed in the field to advance the understanding and application of chirality and quantum effects in quantum information processing, storage and transduction include:

• Exploration of emerging materials such as topological chiral materials, 2D materials and heterostructures, 2D magnets, and hybrid crystals

• Design and evaluation of artificial chiral materials that can be used to control electronic, magnetic, and optical effects

• Integration of multiple categories of materials such as organic molecules and conjugated systems, 2D quantum materials, chiral surfaces, thin films, and nanomaterials

• Fundamental probing of biological processes to understand mechanisms that can be brought into artificial systems

• Improved modeling of chiral systems that go beyond DFT, particularly for larger molecular and hybrid systems that more closely resemble experimental conditions

• Design, implementation, and testing of quantum device architectures to take advantage of chiral-quantum effects

• Matching chiral materials that exhibit quantum effects with properties suitable for existing quantum device architectures

Based on the exciting work that we have reviewed here, and the extensive ongoing efforts in many groups, we anticipate that materials and systems that take advantage of inherent chiralities and interactions with other quantum effects will play an important role in the next revolution in quantum devices.

The authors declare no competing financial interest.

Author Status

Juan José Sáenz passed away on March 22, 2020.