Electronic Transport in Molecular Wires of Precisely Controlled Length Built from Modular Proteins

Abstract

DNA molecular wires have been studied extensively because of the ease with which molecules of controlled length and composition can be synthesized. The same has not been true for proteins. Here, we have synthesized and studied a series of Consensus Tetratricopeptide Repeat (CTPR) proteins, spanning 4 to 20 nm in length, in increments of 4 nm. For lengths in excess of 6 nm, their conductance exceeds that of the canonical molecular wire, oligo(phenylene-ethylenene), because of the more gradual decay of conductance with length in the protein. We show that, while the conductance decay fits an exponential (characteristic of quantum tunneling) and not a linear increase of resistance with length (characteristic of hopping transport), it is also accounted for by a square-law dependence on length (characteristic of weakly-driven hopping). Measurements of the energy dependence of the decay length rule out the quantum tunneling case. A resonance in the carrier injection energy shows that allowed states in the protein align with the Fermi energy of the electrodes. Both the energy of these states and the long-range of hopping suggest that the reorganization induced by hole formation is greatly reduced inside the protein. We outline a model for calculating the molecular-electronic properties of proteins.

Graphical Abstract

Introduction

Proteins are candidate materials for a different approach to nanoscale electronics¹. They self-assemble into highly reproducible complexes, can be engineered at the atomic scale, have a wide range of chemical functionality, and are good molecular conductors, ^2-4 even when they contain no redox-active species. Despite these attributes, there have been no systematic studies of the length dependence of electron or hole transport through intact proteins over a wide range of lengths, except for the case of macroscopic amyloid crystals.⁴ In contrast, the field of DNA electronics has developed rapidly,⁵ because DNA chemistry allows for the synthesis of molecules of arbitrary lengths and controlled compositions. Thus, the length and sequence dependence of charge transport in DNA has been studied in great detail.⁶ The data are well-fitted by a hopping transport model, except at the shortest distances (<2 nm) where quantum interference effects can be observed.⁶ Surprisingly, there is still debate about whether transport across proteins is dominated by tunneling or hopping. Some studies of protein layers in devices have found their conductance to be temperature-independent, ^7-12 interpreted as evidence of coherent tunneling transport. ^{13, 14} Conductance resonances in redox active proteins as a function of surface potential^15-19 have been interpreted in terms of sequential incoherent hops via a (partially) relaxed redox state^{20, 21} although resonant transmission has also been cited as evidence of coherent tunneling.¹³ A versatile protein molecular wire consisting of identical repeat units and of precisely controlled length is required to settle these issues and to establish the performance of proteins as molecular wires for molecular electronic applications. The Consensus Tetratricopeptide Repeat (CTPR) proteins consist of a rigid helix-turn-helix motif that may be repeated many times to form linear structures of up to at least 20 nm in length.²² Here, we explore the dependence of the conductance of a series of CTPR proteins spanning 4 to 20 nm in length in increments of 4 nm. We find that the decay of current with distance is so slow that, for distances in excess of 6 nm, these protein wires outperform the canonical molecular wire oligo(phenylene ethylenene) in the long-range hopping limit.²³ Our measurements show that the long-range transport is not quantum-coherent, but is dominated by a field-free random diffusion process.²⁴ This model is amenable to quantitative calculations of the electronic properties of proteins as molecular electronic components.

Results and Discussion

Synthesis of Consensus Tetratricopeptide Repeat (CTPR) Proteins

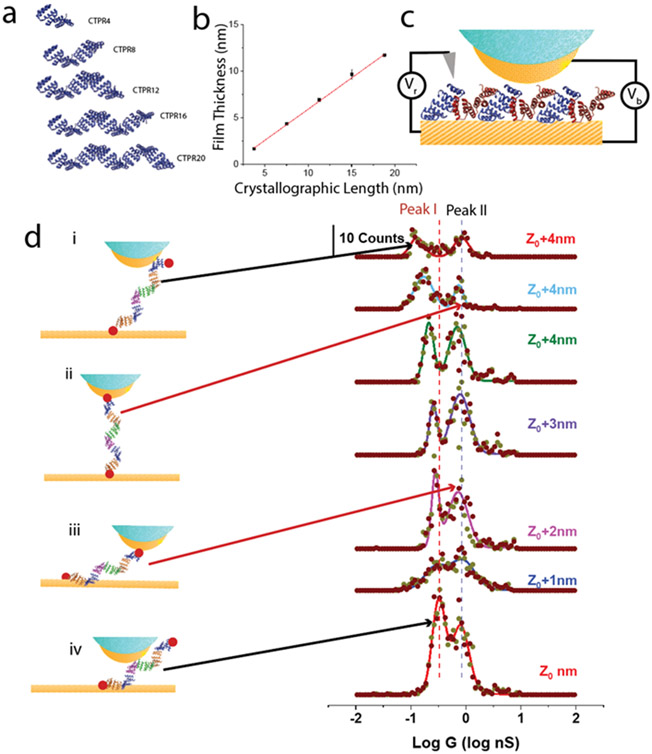
The helix-turn-helix motif of the CTPR proteins is shown in Figure S14. It is readily concatenated to form the linear structures shown in Figure 1a. The oligomers were formed directly by insertion of the appropriate repeated sequences into an expression vector, eliminating the need to chemically connect and purify oligomers of the desired length. Concatamers of CTPRs were created via insertion of a tetra-repeat CTPR (CTPR4) sequence multiple times to create 8, 12, 16, and 20 repeats in the expression vector pPROEX-HTa, with single cysteine mutations at the N- and C- termini (Methods). This resulted in the expression of the series CTPR4, 8, 12, 16 and 20 as shown in Figure 1a. Crystal structures are available for CTPR8 and CTPR20, and each shows the same arrangement of atoms in the repeat unit ²⁵ so the extrapolated structures shown in Figure 1a are believed to be accurate. They correspond to a length of 0.94 ± 0.07 nm per repeat. Mejias et al.⁹ showed that the hydrodynamic radius of a series of CTPR polymers spanning 2 to 20 repeats increased with the number of repeats, and Figure 1b shows the results of our ellipsometric measurements of the thickness of CTPR monolayers formed on palladium substrates. The linear increase of film thickness with the number of repeat units rules out both denaturation of the protein on the electrode and the possibility that the molecules lie flat on the substrate. Plotting this height against the crystallographic length yields a slope of 0.67±0.01 (R² = 0.9996). This slope indicates that the molecules are tilted in the surface monolayer with a tilt similar to that previously reported for a CTPR20 monolayer.²⁶ The HADDOCK docking program ²⁷ shows that close packing is possible with an intermolecular distance of 3.6 nm and an axial displacement of 2.5 nm when neighboring molecules alternate between an N-terminal attachment (blue in Figure 1c) and a C-terminal attachment (red in Figure 1c). This model predicts an angle with respect to the substrate of 46°, close to the 42° derived from the ellipsometric data.

Figure 1: Molecular wires and conductance measurements.

(a) Consensus tetratricopeptide (CTPR) wires synthesized with N- and C- terminal cysteines showing projections of the structures perpendicular to the long axis. (b) Monolayer thickness measured by ellipsometry vs. Crystallographic length. The slope implies a tilt angle of 42°. (c) Conductance measurements: Current measured by an STM probe jumps as contact is made to the molecular layer, shown here for CTPR4 molecules docked in an alternating orientation for which the predicted tilt angle is 46°. V_b is the bias applied to the tip-substrate junction and V_r is the bias applied to a Ag/AgCl reference electrode in the electrolyte solution. Probes are insulated (blue) to within a few nm of their apex, reducing leakage currents to < 1pA. The initial set point (Z₀) was 4 pA with V_b=200 mV (Figure S16). (d) Measured distributions of conductances for CTPR20 as the gap is increased in 1 nm increments from Z₀. Peak 1 in the distribution corresponds to one specific thiol bond and one non-specific contact (i and iv). Peak 2 corresponds to two specific contacts (red dots in ii and iii). Dark red spots = scan up, grey spots = scan down.

STM conductance measurements.

Electrochemical STM measurements were carried out (Figure 1c) as described before.²⁸ The sequence in which the gap is set, molecules captured and current-voltage curves recorded is illustrated in Figure S16. Pd substrates were functionalized using aqueous solutions of CTPR wires, cysteine-terminated at both ends and characterized by FTIR and cyclic voltammetry (Figures S1, S2). Pd probes were prepared with polyethylene insulation, resulting in a leakage current of < 1 pA in the 1 mM phosphate buffer (PB) used for STM measurements.²⁹ The initial set-point, Z₀ was obtained with a current of 4 pA at a bias of 0.2 V, after which the servo was disabled and the tip withdrawn by some additional distance as indicated on the figures. The substrate was held at 0V (V_r in Figure 1c) with respect to an Ag/AgCl reference (utilizing a 10 mM salt bridge) and the bias sweep (± 200 mV, 1 s per sweep) was started automatically when a current >50 pA was detected, indicating that a molecule was contacted by the electrodes. Data were recorded for up to 120 s, after which the gap was stabilized again under servo control and the process repeated. The recorded current vs. voltage curves (Figure S3) are linear and reversible and the slope of each yields a single molecule conductance. Distributions of conductance for CTPR20 are shown in the middle of Figure 1d, and they show the two peaks (Peak I, Peak II) characteristic of one specific contact and a second non-specific contact (Peak I) and two specific (sulfur-metal) contacts (Peak II). We have discussed the origin of these two features in detail elsewhere²⁸ but briefly, no current is observed at all in the absence of at least one specific chemical contact between the protein and one electrode. In the absence of a second specific contact, the chemical nature of a second contact is unknown, except for the fact that it takes some tens of seconds to form, and the frequency of such contacts is dependent on the surface chemistry of the second electrode (hydrophilic vs. hydrophobic). Alternatively, when the molecule is functionalized such that two specific chemical contacts are possible (i.e., thiols at the N- and C- termini in the present case) a second high conductance peak is found at about ten times the conductance of the peak observed in the molecule with only one specific chemical attachment. This two peak distribution is largely unaltered as the gap is increased in 1 nm increments up to Z₀+6 nm, with contacts essentially vanishing at Z₀+7 nm. If we use the value for Z₀ of 2.5 nm that was previously deduced using a molecular ruler,³⁰ these results would suggest a film thickness of ~2.5 nm (assumed Z₀) plus the additional 6 nm, or 8.5 nm, which is less than the 11.7 nm measured for the CTPR20 monolayer thickness. However, we have found that we could advance the probe by as much as 5 nm to contact the substrate from the set-point conductance in the CTPR20 film, suggesting that Z₀ is closer to 5 nm in these films (Figure S4) so that contact is actually lost at about 11 nm displacement, consistent with the known film thickness. This finding suggests that Z₀ is considerably increased in a proteinaceous medium (as opposed to in a solvent ³⁰ – note that the probe is buried inside the protein film in the present measurements). The jump in current (from 4 pA to >50 pA) that occurs when a ‘non-specific’ contact is made must reflect a yet more favorable contact chemistry than a Van der Waals contact (such as the side-chain amine of a lysine interacting with the probe metal).

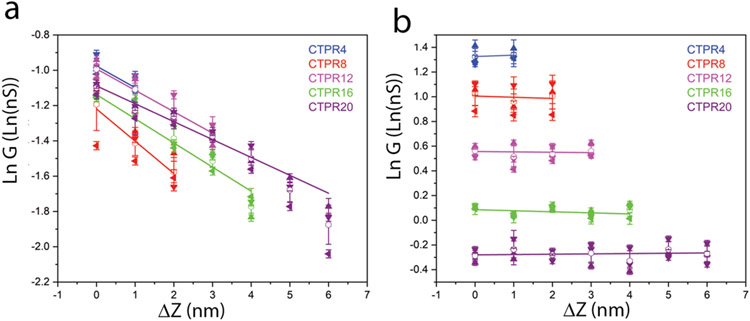
As observed previously for other proteins,³¹ Peak I moves to lower conductance as the gap is increased, because this peak arises from a path length that, on average, increases with gap size (i and iv in Figure 1d). Peak II is independent of the gap change (within experimental uncertainty) because it arises from contacts to the two terminal cysteines, so that the path length does not change with gap size (ii and iii in Figure 1d). (Note that the contribution of direct tunneling is a maximum of 4 pA at the smallest gaps, less than 10% of the smallest through-molecule current of 50 pA at 0.2V and thus may be ignored). This lack of dependence on gap size can only occur if the transport path for Peak II is through the molecule as opposed to directly across the monolayer. A summary of the values of peak conductance vs. the change in gap distance is given in Figure 2 for Peak I (2a) and Peak II (2b) with data tabulated in Tables S1a-e. For a tunneling process, the conductance decays with distance, L according to

$$G=G_0\text{exp}\left(-\frac{L}{\lambda }\right)$$ (1)

where G₀ is the quantum of conductance. The corresponding values of (exponential) decay lengths (obtained from the slopes of Peak I data in Figure 2a) are listed in Table 1. They are much larger than expected for a tunneling process. Conductance values averaged over all values of ΔZ for Peak II are given in Table 2. Examples of conductance histograms for all gap values for all five proteins are shown in Figures S5a-e.

Figure 2: Conductance peak values as a function of gap increment.

(a) Data for Peak I, showing that conductance decreases exponentially with distance with a decay length λ ~ 8 nm (Table 1). (b) Data for Peak II showing that conductance is independent of gap distance within experimental error. Data points are the mean and error bars are the standard deviation (SD) from three independent repeats of each run (different symbols for each run) in which histograms like those in Figure 1d were collected and fitted.

Table 1:

Decay lengths (λ) derived from the dependence of Peak I conductance on tunneling gap.

Molecule	dln(G)/d(ΔZ) (nm−1)	λ (nm)
CTPR 4	−0.122*	8.2*
CTPR 8	−0.183 ± 0.02	5.5 ± 0.5
CTPR 12	−0.121± 0.02	8.3 ± 1.2
CTPR 16	−0.137 ± 0.02	7.3 ± 0.8
CTPR 20	−0.101± 0.02	9.9 ± 1.6

^*There were only two data points for CTPR 4 so no fit uncertainly is available.

Table 2:

Conductances averaged over measurements made as a function of tunneling gap for Peak II (error bars are SD).

Molecule	Crystallographic Length (nm)	Average Conductance (nS)
CTPR 4	3.76	3.78 ± 0.02
CTPR 8	7.52	2.70 ± 0.07
CTPR 12	11.28	1.72 ± 0.03
CTPR 16	15.04	1.08 ± 0.03
CTPR 20	18.8	0.76 ± 0.02

Tunneling versus hopping

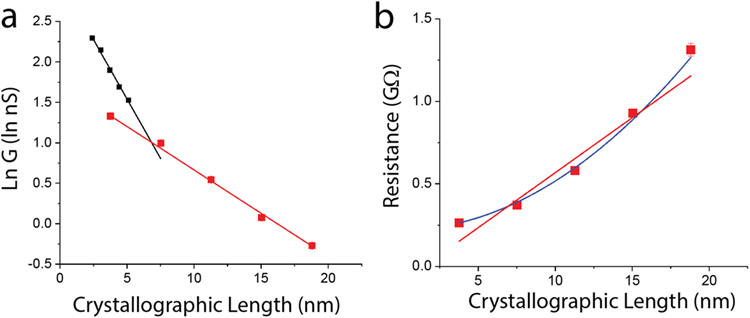
In principle, measurements of the length-dependence of conductance can shed light on the transport mechanism. In tunneling, the resistance of the molecule increases exponentially with length (i.e., conductance decreases exponentially as in Equation 1) ³². A linear dependence of resistance on length is a signature of hopping,⁶ though other power law dependencies are possible.²⁴ The transition from tunneling to hopping transport has been studied in films of oligo(phenyleneimine) ³³ and oligo(phenylene ethylenene). ²³ An initial rapid exponential increase in resistance was followed by a much more gradual increase for distances > 4 nm, marking the transition to hopping transport. In those papers, data for the hopping regime (i.e., linear length dependence) was fitted by an exponential. The fits were good despite the use of the wrong function (exponential in place of linear) illustrating the challenge of fitting a gradual decay over a small range of distances. The Peak II conductances for all five molecules (averaged over all gap sizes) are plotted vs. crystallographic length in Figure 3a (error bars are standard deviations and are smaller or equal to the symbol size). Fitted to Equation 1 these data yield a decay length, λ, of 9.3 ± 0.05 nm. This is within the range of decay lengths (average = 7.8 ± 1.6 nm) determined for each molecule using the ‘sliding contact’ method (Peak I, Table 1). Thus, the two measurements are consistent with each other, lending credence to the more precise value obtained from Peak II.

Figure 3:

(a) Conductance decay fitted to an exponential with a decay constant 1/λ = 0.107 ± 0.003 nm⁻¹ (red points in (a), R² = 0.998). The black data points (data from ref. 23) are for the region of hopping transport for the organic molecular wire oligo(phenylene ethylenene), illustrating the relative improvement offered by protein wires for distances greater than ~ 6 nm. (b) The increase of resistance with length departs significantly from the linear behavior usually expected for hopping (red line, R²=0.925) but is well-fitted by a square-law dependence (blue line, R² = 0.994). Error bars are approximately equal to symbol sizes.

This long decay length accounts for the high conductance of large proteins. As previously observed, the contact resistance (inverse of the conductance intercept at zero distance) is high (red data points, Figure 3a), much higher than that for an oligo(phenylene ethylenene) (OPE - black data points, Figure 3a) one of the family “Tour wires” widely used in molecular electronics.²³ However, the decay length for the OPE in the hopping regime is significantly shorter than that for the CTPR wires, so for distances in excess of ~6 nm, the protein is the better molecular wire. Amdursky et al.³⁴ arrived at a similar conclusion in their 2014 review.

The fit to an exponential decay is excellent (R²=0.998), and the data span a sufficient range to allow a comparison to the linear dependence of the resistance on length predicted for incoherent hopping transport ²⁴ (Figure 3b). There is a significant departure from a linear dependence, but, as discussed below (and in reference²⁴) hopping transport in a field-free environment follows a square law dependence on distance (the field distribution in the electrode-protein-electrode system is discussed below). This is shown by the blue line in Figure 3b. The fit is just as good as the exponential, leaving both tunneling and hopping as possibilities.

Quantum or not?

Temperature measurements are, in most cases, the most direct way to test for quantum vs. classical transport, but they are very difficult to implement at the single molecule level. However, another test of simple tunneling theory lies in the energy dependence of the decay length. If the barrier to charge injection can be described by a rectangular potential of height ΔE where ΔE is the energy difference between the resonance peak and the electron injection energy, then the inverse decay length is given by:

$$\frac{1}{\lambda }=2\sqrt{\frac{2m^{\ast }\Delta E}{{\hslash }^2}}$$ (2)

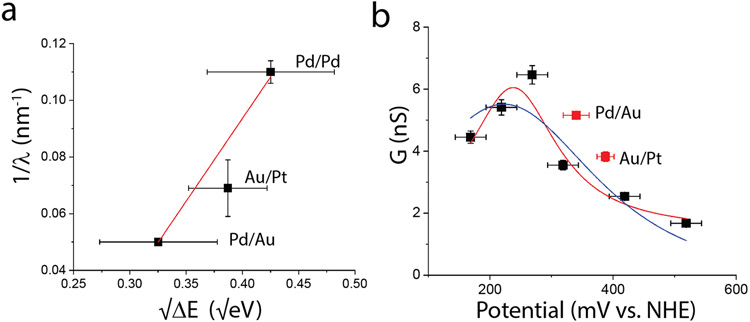
where m* is the effective mass of the charge carrier, e is the electronic charge and ΔE is the energy difference expressed in eV. In addition to the existing data (Pd electrodes tied to a 10 mM reference) we carried out measurements of decay length using a Pd tip – Au substrate (Pd/Au) and a Au tip-Pt substrate (Au/Pt). For Pd/Au we took the average of the rest potentials iii and iv in Table S2, and for Au/Pt we used the average of iv and v in Table S3, adding 210 mV to yield the values vs. the normal hydrogen electrode (NHE). (The electrochemical properties of Au and Pt functionalized with CTPR are given in Figure S9.) ΔV is the difference between the average electrode potentials and the peak transmission energy of 237.8 mV vs NHE (see below). The inverse decay length, 1/λ, is plotted vs. $\sqrt{\Delta E}$ in Figure 4a, showing that the relative injection energy of the carriers does indeed modulate the decay length. Despite significant experimental uncertainties, two features are robust: The intercept of the linear fit (red line in Figure 4a) with the vertical axis at $\sqrt{\Delta E}=0$ is −0.14±0.02 nm⁻¹. No fit is possible with a zero intercept as required by equation 2. Secondly, the slope of the linear fit is 0.58±0.07 ${\text{nm}}^{\text{-}1}∕\sqrt{V}$ (R²=0.986), which, according to equation 2 is $\sqrt{\frac{m^{\ast }}{m_e}}\times 10.2{\text{nm}}^{\text{-}1}∕\sqrt{\Delta E}$. This leads to an unphysically small effective carrier mass of ~3X10⁻³ m_e. Put another way, if $\frac{m^{\ast }}{m_e}\sim 1$, a barrier much less than 1 mV would be required to account for the long decay lengths. This argues against a simple tunneling model of long-range transport.

Figure 4:

(a) Energy dependence of decay length: Dependence of the inverse decay length ¹/_λ on the square root of the difference between the injection energy and the resonance peak, showing that the decay length depends on the injection energy of the carriers. However the slope and intercept of the fit are not consistent with a simple tunneling process. (b) Injection into allowed states: Conductance as a function of electrode potential for CTPR8 (data for Peak II). Black squares are Pd/Pd relative to a reference electrode, here presented on the NHE scale. Red squares are for other metal combinations (as labeled) with potentials as listed in Tables S2 and S3. The red line is a fit of the Pd/Pd data to the Breit-Wigner formula for resonant tunneling and the blue line is a fit to the formula for a two-step hopping process (Eqn. 3). Both processes may apply: The Breit-Wigner formula describing the first resonant injection from the electrodes and the two-step model describing the individual hops within the bulk of the protein.

Charge injection into allowed states

If the transport is via hopping, a prerequisite is charge injection into allowed states.²⁴ The injection energy of the electron (or hole) may be controlled by altering the surface potential of the electrodes and we have used this approach to measure conductance as a function of potential, finding a resonance in the vicinity of 250-300 mV on the NHE scale for several proteins.³⁵ Following the procedures described in ref. ³⁵ we measured the conductance of CTPR8 wires as a function of potential (within a range of potentials where Faradaic currents are minimized, Figure S2), obtaining the conductance distributions shown in Figure S6. A 10 mM Ag/AgCl salt-bridged reference was used to avoid salt contamination of the STM cell ²⁸ but we found that, in the 1 mM PB, it held the system (substrate plus reference) at a potential between that of the reference and the rest potential of the electrode alone (See Figure S7 and discussion in the caption). Measured rest potentials vs. the 3 M reference are listed in Table S2. Averaged values (which give the effective Fermi energy of the electrode system ³⁵) for various electrode metal combinations are given in Table S3 (converted to the NHE scale by adding 210 mV).

Values of conductance for Peak II for CTPR as a function of the substrate potential with respect to the reference electrode are summarized in Figure 4b. This resonance is similar to that observed in several other non-redox proteins (c.f., ref. ³⁵ where the potential scale should be reduced by about 40 mV to account for the revised calibration of the 10 mM reference in 1 mM phosphate buffer - Figure S7). As a check on the validity of using the averaged potentials calculated from rest potentials, we have plotted the Peak II conductance values for CTPR8 functionalized Pd/Au and Au/Pt electrodes as the red points in Figure 4b. The data taken by the two methods agree qualitatively with a ~ 60 mV difference in the potential scale. Fitted by the Breit-Wigner formula (red line) we used in the earlier study³⁵ the peak is found to be at with E₀ = 237.8 ± 13 mV with a half-width of 175 ± 66 mV (a similar fit for Peak I yielded E₀ = 239.5 ± 16 mV with a half width of 116 ± 83 mV Figure S8). Thus, for all the metal combinations used in the current study (Table S3) charge injection occurs within the half width of the band of allowed states in the molecule.

The quantum-coherent Breit-Wigner description alone is surely not adequate. As we discuss below, transport likely consists of two distinct processes: a quantum tunneling injection of charge at the contacts into vibrationally modulated molecular states (for which the decay length is very short³⁶) and long-range hopping transport in the bulk of the protein (for which the decay length is very long). The injected charge must be in resonance with both the initial states that it is injected into, and with the states responsible for long-range hopping. The long-range hopping occurs between a multiplicity of sites, but we have used the simplest (single site) two step model of Pobelov et al.²¹ (based on the theory of Kuznetsov and Ulstrup²⁰). This model describes a process in which an electrode first reduces a molecular site, which is then subsequently oxidized by the second electrode, giving the following result for the conductance enhancement as a function of potential:

$$G=\frac{G_{peak}}{\text{cosh}(w[E-E_0])}+G_b$$ (3)

where E₀ is the formal potential of the redox center that traps the electron, w is a parameter that depends on the potential distribution inside the molecule and is used here as a freely-adjustable width parameter. The resonance enhancement of the current is G_peak and it is given (at low bias) by 910 exp(−9.73λ) nS where λ is the reorganization energy in electron volts. The blue line in Figure 4a shows a fit of Equation 3 with G_peak = 5.5 nS, w = 0.0077 mV⁻¹ and E₀ = 222 mV, with the background, G_b, being negligible. The corresponding reorganization energy, λ, is 0.52 eV (subject to considerable uncertainty both because the model is an oversimplification and because the peak value of current is probably affected by many other factors). Conductance resonances have been observed at the formal potential of a redox site in a protein^{15, 37-42} but it is important to stress that the proteins studied here contain no readily reduced or oxidized centers. The most readily oxidized amino acid residues (tyrosine and tryptophan) have oxidation potentials of about 1 V on this scale,^{43, 44} some 700 mV positive of the observed resonance. Nonetheless, we believe these residues to be the source of the states that mediate charge transfer via vibronic interactions, both because they are the most readily oxidized, and because tyrosine is clearly responsible for the long-range hopping transport reported in amyloid crystals.⁴ We discuss below how the difference in fluctuations between the solvent environment and interior of a protein can lead to greatly reduced reorganization energy.

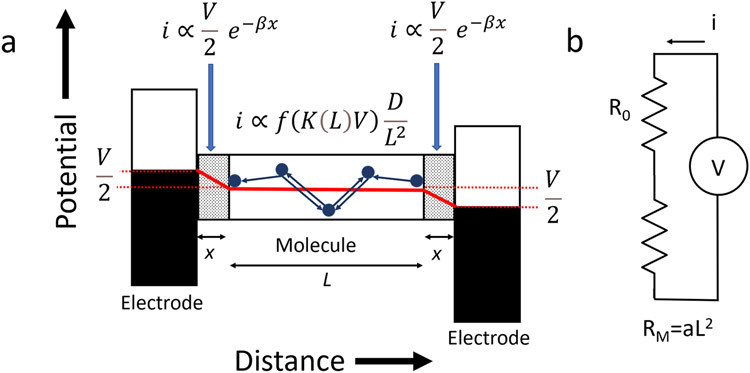
Small external field in protein gives square-law decay.

A model for the molecular charge transfer is shown in Figure 5a. The large contact resistance (compared to that of the OPE, for example) implies that there is a significant barrier to charge injection, giving rise to a substantial electric field at the contact regions (designated x in the figure). Experiments with engineered contacts show that in these regions there is a rapid decay of current with distance, with an exponential decay constant, β, of 3.4 nm^{−1 45} corresponding to a decay length of ~0.3 nm (which, according to equation 2, corresponds to a potential barrier of ~0.1V which is also the onset bias for telegraph noise²⁸). A fraction, K(L), of the applied voltage appears across the molecule because of the contact resistance (of 222 ± 2 MΩ, the intercept of the blue curve in Figure 3b). K(L) is readily derived from elementary circuit theory (Figures 5b, S13 and Table S4). For the longest proteins, K(L) approaches 1, however, the external field in the protein is fairly constant as a function of length (Table S4) at about 10 mV/nm for the highest applied bias of 200 mV. There are seven (6 tyrosines and one tryptophan) aromatic residues in each helix-turn-helix motif of the CTPR protein (Figure S13), with several separation distances within the 1.5 nm range considered to be the limit of charge transfer via tunneling.⁴⁶ Thus the potential difference owing to the applied field is on the order of ~10 mV between any pair of aromatic residues. This is less than thermal energy and very much less than the intrinsic variation of potential between amino acid residues within proteins (see for example Figure 8 of Aksimentiev and Schulten⁴⁷). Thus, although the applied bias must play an important role (see below) charge motion is dominated by thermal fluctuations and the intrinsic potential variations inside the protein. In consequence, a charge, once injected, undergoes a random walk that is essentially unbiased. The corresponding transit time is given by the mean time of first passage, which is $\tau =\frac{L^2}{2D}$ (for 1-D diffusion) where L is the length of the molecule and D the diffusion constant. The current (at a given bias) is proportional to $\frac{1}{\tau }$, leading to an increase of resistance with distance (Figure 5b) given by

$$R(L)=R_0+a{L}^2$$ (4)

Figure 5.

(a) Model for transport in a protein molecular junction. Shaded regions are the contacts and the red line show potential drop vs. distance. Small arrows indicate flow of holes. (b) Circuit model for resistance vs. length prediction. R₀ is the contact resistance.

This yields an excellent fit to the decay data, shown by the blue line in Figure 3b with R₀ = 222 MΩ and a = 0.003 Ω- nm². (This square-law dependence on length is also a result given by Jortner et al. for unbiased hopping.²⁴) Thus our decay data are consistent with a model of unbiased (free) diffusion, the lack of a strong external driving potential accounting for the departure from the linear length dependence of resistance usually expected for hopping conductors.

It should be noted that while small, the externally applied field cannot be neglected, since, following the model in Figure 5a, the injected current at the contact barrier must be equal to the diffusion current, and, in order for the overall behavior to be Ohmic, the voltage dependence of the diffusive transport (f(K(L)V)) must also be linear. This is impossible to achieve with a simple 2 step process (Figure S15) however, this is likely a poor model for a process involving at least 28 hopping sites (CTPR4) with a weak driving force such that many hops occur both with and against the external field.

Reorganization energy must be reduced inside the protein

The most readily oxidized amino acid residues are tyrosine and tryptophan^{43, 44} with oxidation potentials some 700mV removed from the observed resonance. The equilibrium reorganization energy in solution for these oxidations has been estimated as 0.5 to 2eV,⁴⁸ so the observed resonance could be a consequence of reduced reorganization in the interior of the protein. Matyushov^49-51 has quantitatively accounted for the reduction in reorganization energy that occurs as a redox center is moved further into the interior of a protein, in terms of the additional long relaxation times inside the protein. If the probability of an electron hop is high enough, transfer can occur before the charged site has fully relaxed, leading to an effective reduction in reorganization energy. A second argument for reduced reorganization energy lies in the magnitude of the currents and the large decay length. Figure S15 shows how currents in a simple two step process are dramatically reduced as reorganization energy is increased. Current would become vanishingly small in a multistep process with the full equilibrium reorganization energy at each site. Furthermore, long-range hopping ^{52, 53} requires a small activation energy. Matyushov^49-51 has laid out a framework for calculating the effective reorganization energy, λ_r, that controls a reaction rate inside a protein. Residues in the interior of a protein are subject to a spectrum of relaxation times that is broader (with slower components) than those on the hydrated external shell of the protein. The key question to be answered is whether tunneling transitions occur rapidly enough so that the occupied sites are only partly relaxed. This requires that the fluctuations be calculated at each aromatic site for the charged and neutral states. Such a calculation is possible using molecular dynamics simulations, and the probability of a transition as well as the degree of reorganization can, in principle, be calculated. Extended to all pairs within the Dutton radius of each other,⁴⁶ this calculation should quantify the extent to which reorganization is reduced and permit a calculation of the diffusion current.

Conclusions

The use of the modular CTPR proteins has permitted the construction of a series of molecular wires of controlled length spanning 4 to 20 nm. The slow decay of current with length demonstrates the potential of proteins as molecular electronic components. Over long distances, they make better wires than molecules designed for the purpose, can self-assemble in complex circuits and can be engineered at the atomic scale with recombinant technology. The series of protein wires we have synthesized has allowed for a study of long-range transport in these non-redox active proteins over a range of lengths. Charge injection from noble-metal electrodes is resonant with only-slightly relaxed electronic states of the protein, likely associated with tyrosine and tryptophan. This results in hopping transport. With a weak overall driving force, the decay of current with distance follows a square law dependence on length. The good fit to an exponential decay is accidental and not an indication of quantum coherent behavior. Both the long diffusion length and the presence of states well-removed from the equilibrium oxidation energies suggest hole transport with greatly reduced reorganization energy. The next steps are quantitative implementations of the model described here, and its use as a design tool for single-molecule protein electronic devices such as polymerases for sequencing DNA⁵⁴ or proteasomes for sequencing of proteins.⁵⁵

Methods

CTPR Expression

All protein expression plasmids were derived from wild type tetra-repeat CTPR (CTPR4) cloned in the expression vector pPROEX-HTa. Design of larger constructs (8,16, & 20 repeats) was accomplished through digestion and ligation of the core repeat sequence of the CTPR open reading frame using the complementary restriction sites BamHI and BglII. Briefly, the core repeat sequence was extracted via double-digest of the aforementioned restriction sites, followed by ligation of the fragment into the BamHI digested plasmid already containing CTPR repeats, thereby achieving concatenation of multiple CTPR repeats. Single cysteine mutations were introduced to both N and C-termini using the following mutagenic primer pairs:

CTPR-N-Cys-Forward (5’-CAGTGATTACGATATCCCAACG-3’),

CTPR-N-Cys-Reverse (5’-CAGCTGTGATGGTGATGGTGATG-3’),

CTPR-C-Cys-Forward (5’-CAGTTGAAAGCTTGGCTGTTTTG-3’),

CTPR-C-Cys-Reverse (5’- CAGCTACCCTGTTTCTGTTTAGC-3’).

Expression plasmids (pPROEX-HTa) for CTPRs were transformed into BL21 (DE3) competent cells for protein expression. Cultures were grown in LB medium at 37 °C until an A₆₀₀ of 0.8 was reached. Protein expression was induced via the addition of isopropyl-β-D-thiogalactopyranoside (IPTG), at final concentration of 200 μM. Induction temperature was 30 °C and induction lasted for 4 hrs. Cells were harvested via centrifugation, and subsequently lysed using a combination of lysozyme (1mg/mL culture) and sonication. Lysis was performed in a 0.5 M Urea buffer (0.5 M Urea, 0.5 M NaCl, 10 mM immidazole, 20 mM phosphate, 5% glycerol, pH 8.0) for improved solubility of the proteins. Purification was carried out via His-tag capture on a 5 mL Cytiva HisTrap Ni²⁺ affinity column using the same lysis buffer, and the protein was eluted with 0.5 M NaCl, 0.5 M imidazole, 20 mM phosphate, 5% glycerol, pH 8.0 buffer. Purity was assessed through SDS-PAGE, and protein size was verified with MALDI-MS.

STM Conductance Measurements

200 nm of Pd, Au or Pt were deposited onto a 10 nm Cr adhesion layer on four-inch p-type Si wafers using an e-beam evaporator (Lesker PVD 75). High density polyethylene-coated Pd and Au probes were prepared as described previously ^{28, 29}. Conductance measurements were made in 1 mM phosphate buffer, pH 7.4, using a PicoSPM (Agilent) following the procedure described elsewhere ²⁸. Monolayers of CTPR were prepared by immersing the chip in a 1 μM CTPR solution for ~16 hrs. After functionalization, the chip was taken out, rinsed with water, blown dry with nitrogen, and used immediately. To avoid forming CTPR aggregations in the solution, a 50 mM tris buffer pH 7.4 containing 10 mM TCEP, 200 mM NaCl, 10mM (NH₄)₂SO₄ and MgCl₂ was used. The surface functionalization was characterized by Fourier transform infrared (FTIR) spectroscopy. FTIR spectra taken from functionalized Pd substrates are given in Figure S1. Thickness of the monolayer was measured on a Gaertner L 123b Ellipsometer (Gaerner Scientific Corporation). A refractive index of 1.5 was used for a thin organic layer. Five measurements on different locations on the chip were conducted to calculate the mean value of the monolayer thickness.

Electrochemical Measurements

A salt-bridged reference electrode was constructed as described previously ²⁸ using 3M KCl for the rest potential measurements (210 mV on the NHE scale) and 10 mM KCl for the conductance measurements (nominally 360 mV on the NHE scale, but see Figure S7). Rest potentials were measured with a Fluke 177 meter (input impedance > 10⁷Ω) and after ~ 10 minutes stabilization time, potentials were stable to within ±5 mV over a period of hours. Sample to sample variation was characterized by repeated measurements with CTPR8 or CTPR16 functionalization and as a function of geometry (STM cell or beaker) to give the uncertainties listed in Table S3. Measurements made with a biased reference and then with different combinations of electrode metal (no reference) showed that the potential of the STM substrates connected to the 10 mM reference lay between the potential of the reference and the rest potential of the substrate (Figure S7).