Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2021 Sep 14;21(19):8103–8110. doi: 10.1021/acs.nanolett.1c02470

Breakdown of Universal Scaling for Nanometer-Sized Bubbles in Graphene

Renan Villarreal †,*, Pin-Cheng Lin †, Fahim Faraji ‡,, Nasim Hassani §, Harsh Bana †, Zviadi Zarkua †, Maya N Nair ∥, Hung-Chieh Tsai ⊥,#, Manuel Auge @, Felix Junge @, Hans C Hofsaess @, Stefan De Gendt ⊥,#, Steven De Feyter Δ, Steven Brems ⊥, E Harriet Åhlgren ∇, Erik C Neyts ‡, Lucian Covaci , François M Peeters , Mehdi Neek-Amal §,*, Lino M C Pereira †,*
PMCID: PMC9286314  PMID: 34519503

Abstract

graphic file with name nl1c02470_0006.jpg

We report the formation of nanobubbles on graphene with a radius of the order of 1 nm, using ultralow energy implantation of noble gas ions (He, Ne, Ar) into graphene grown on a Pt(111) surface. We show that the universal scaling of the aspect ratio, which has previously been established for larger bubbles, breaks down when the bubble radius approaches 1 nm, resulting in much larger aspect ratios. Moreover, we observe that the bubble stability and aspect ratio depend on the substrate onto which the graphene is grown (bubbles are stable for Pt but not for Cu) and trapped element. We interpret these dependencies in terms of the atomic compressibility of the noble gas as well as of the adhesion energies between graphene, the substrate, and trapped atoms.

Keywords: graphene, nanobubbles, aspect ratio, scanning tunneling microscopy

Owing to its unrivaled elasticity and strength,1,2 graphene is able to hold matter at extreme pressures in the form of bubbles with dimensions down to the nanometer scale.3−6 These bubbles offer new opportunities to explore chemistry and physics under the extreme conditions that both graphene and the trapped matter are subject to, for example, strain-induced pseudomagnetic fields in graphene7−9 and high-pressure chemical reactions.10,11 Similar nanobubbles in other 2D materials such as MoS2 and h-BN are also being investigated as single-photon emitters for quantum communication.12,13

While previous research has mostly dealt with bubbles with a radius of few nm and larger, the subnanometer regime remains largely unexplored. Here, we report the formation of graphene nanobubbles with a radius down to below 1 nm, filled with He, Ne, and Ar. Delving into the physical mechanisms that determine the stability and shape of these subnanometer bubbles reveals that they constitute a fundamentally different regime, exhibiting an extreme aspect ratio, tensile strain, and pressure. The unique properties of this subnanometer regime open an unexplored ground for applications of nanobubbles in 2D materials.

The properties of graphene bubbles with a radius of a few nm and larger are relatively well understood on the basis of elasticity theory as well as graphene’s elastic properties and its van der Waals (vdW) attraction to the substrate.5 In this regime, bubbles have been observed on various substrates (e.g., Ir, Pt, h-BN, SiO2) with a variety of trapped substances (e.g., water, noble gases, hydrocarbons),3,5,6,14,15 which do not appear to significantly affect the bubble stability.5,6 The substrate and trapped substance do affect key properties, such as shape (in particular the aspect ratio) and the pressure inside the bubble.5,6 This dependence is largely determined by the balance of the adhesion energies: between graphene and the substrate (γGS), between the substrate and the trapped substance (γSb), and between the graphene and the trapped substance (γGb).5 A particularly striking feature demonstrated for nanobubbles in the few nm regime and larger is that the aspect ratio exhibits universal scaling

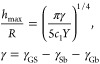graphic file with name nl1c02470_m001.jpg 1

where hmax is the bubble maximum height, R is the bubble radius at the base, c1 is a constant (0.7), and Y is the Young modulus.5 Here, by combining scanning tunneling microscopy (STM) measurements with molecular dynamics (MD) simulations and density functional theory (DFT) calculations, we show that this universal scaling breaks down at small R (near 1 nm and below). We also observe that the bubble stability is strongly dependent on the substrate. We interpret these dependencies in terms of the role of the atomic compressibility of the noble gases as well as of the adhesion energies (γGS, γSb, and γGb). Moreover, these nanobubbles are found to induce high levels of strain (of the order of 10%) on the overlaying graphene and are predicted by our MD simulations to hold the noble gas atoms under extreme pressures (exceeding 30 GPa).

Experimental Details and Basic Characterization

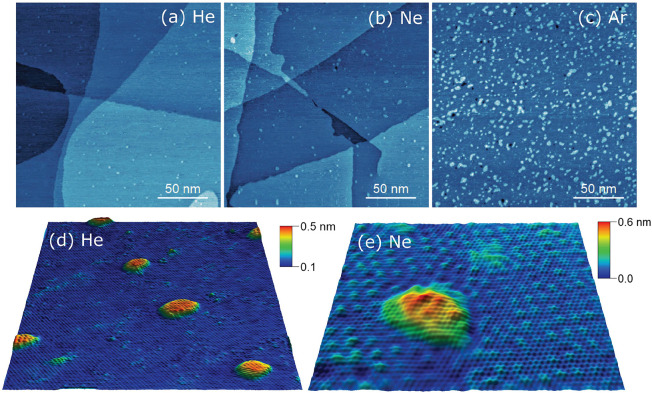
Our samples consist of epitaxial graphene grown by chemical vapor deposition (CVD) on epitaxial Pt(111) and Cu(111) thin films grown on sapphire(0001) substrates.16,17 Nanobubbles are formed by implanting noble gas ions (He, Ne, and Ar), with a kinetic energy of 25 eV, with perpendicular incidence with respect to the surface. Bubbles were found to only form for graphene on Pt(111) (Figure 1), not for graphene on Cu(111) (Figure S1). In the following, we will focus on Pt(111) and return to Cu(111) further below when discussing how the bubble stability depends on the substrate. Ion implantation has been previously used to form graphene nanobubbles of noble gases.3,14,15 In contrast to the previous studies, where ion beams with energies of 500 eV and higher were used, our approach is based on ultralow energy (ULE) ion implantation. Such low energies are crucial to minimize irradiation-induced damage. Based on our MD simulations (Figure S2), we selected 25 eV (surface normal incidence) as sufficiently high for a significant fraction of the ions to be transmitted through the graphene layer but sufficiently low to minimize carbon atom displacements (i.e., formation of vacancies and related point defects). While ULE ion implantation has been previously used for doping of graphene (e.g., with B and N18−20) where vacancies are required (which allows for substitutional incorporation of the dopant atoms), such defects must be avoided in the context of the present work so that the intrinsic elastic properties of graphene are maintained. The graphene bubbles observed in our samples are identified as nanometer-scale protrusions on the surface of graphene (grown on Pt(111), implanted with the noble gases) as shown in the STM topographies in Figure 1. The fact that the graphene lattice can be resolved even over these protrusions confirms that the implanted noble gases are intercalated (Figure 1d,e), that is, the protrusions are not due to matter deposited on top of graphene. The fraction of surface that is covered by bubbles (for the same implanted fluence) was found to vary between implanted noble gas elements (Figure 1a–c). This dependence is likely due to the different transmission and backscattering probabilities for the different elements (cf. Supporting Information). The high structural order of the irradiated surfaces is supported by our atomic-resolution STM measurements on the as-implanted surfaces (Figure 1d,e) and by the integrity of the moiré superstructure in most of the surface with only minor disorder (Figure 1e). This minor disorder is due to defects introduced during the implantation process, and it can be seen in the STM topographies as point-like features (protrusions and depressions) perturbing the periodicity of the atomic lattice (Figure 1d,e) and of the moiré superstructure (Figure 1e) (cf. Supporting Information). Indeed, Raman spectroscopy measurements show some degree of disorder (Figure S6). Since the selected implantation energy is below the threshold for vacancy formation (Figure S2), this disorder is likely associated with the breaking of C–C bonds without the production of C vacancies and likely resulting in locally enhanced interaction of the Pt atoms at the interface, leading to the subtle defect features observed by STM.

Figure 1.

Figure 1

Open in a new tab

STM micrographs showing (a) He, (b) Ne, and (c) Ar bubbles in graphene/Pt(111). (d,e) STM micrographs (20 × 20 and 10 × 10 nm2, respectively), with atomic resolution, showing a continuous graphene atomic lattice, in particular, over the bubbles.

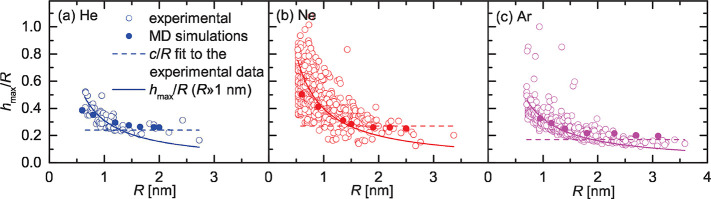
Breakdown of Universal Scaling at Low Radius

The radius and aspect ratio of each bubble, for the different elements (He, Ne, and Ar), are plotted in Figure 2. A clear trend is observed for all three gases. For larger R values (>1 nm), the aspect ratio tends to converge to a constant value of about 0.2, which is in agreement with the universal scaling previously observed for bubbles with a radius of few nm and larger.5 However, as R approaches the subnanometer regime, the universal scaling breaks down, showing an increase in the aspect ratio and approaching 1 for Ne bubbles. From the experimental data in Figure 2, we calculated, for each gas (He, Ne, Ar), an average value for hmax0 (from the 10% smallest bubbles) and an average value for 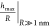Inline graphic (from the 10% largest bubbles). These values are compiled in Table 1.

Figure 2.

Figure 2

Open in a new tab

hmax/R as a function of R obtained from STM micrographs such as those shown in Figure 1 (empty circles) and from MD simulations (filled circles), for (a) He, (b) Ne, and (c) Ar bubbles in graphene/Pt(111). Each experimental data point corresponds to one bubble. The solid line is a fit with the function (hmax/R = c/R). The dotted line corresponds to the value of 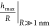Inline graphic.

Table 1. Aspect Ratio and Related Parametersa.

element hmax0 [Å] 2rvdW [Å] β [au] ⟨Δz⟩ [Å]
graphic file with name nl1c02470_m008.jpg
 γ [eV·Å–2]
He 2.9(±0.5) 2.86 –0.152 0.31 0.24(±0.05) 0.08
Ne 3.5(±0.8) 3.16 –0.266 0.49 0.27(±0.07) 0.13
Ar 3.1(±0.6) 3.88 0.081 0.29 0.17(±0.03) 0.02
Open in a new tab
a

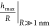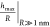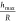hmax0 and Inline graphic are obtained from the data in Figure 2. hmax is the average of hmax taken over the 10% smallest bubbles. Inline graphic is the average Inline graphic taken over the 10% largest bubbles. The values inside the brackets are the standard deviation associated with the respective averages. ⟨Δz⟩ is the average z-motion amplitude obtained from the MD simulations, for the smallest bubbles (radius of ∼6 Å for He and Ne and ∼9 Å for Ar). 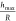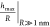γ is calculated using eq 1 with Inline graphic given by Inline graphic. 2rvdW is the vdW diameter (from ref (21)), and β is the atomic compressibility (from ref (22)).

Bending rigidity (neglected in the derivation of eq 1) becomes more important as the bubble dimensions decrease down to <1 nm.5 However, as described in the Supporting Information, the effect is still negligible for the bubbles described here and is in fact in the opposite direction (decreases the aspect ratio). The observed breakdown of the universal scaling must therefore originate from a different mechanism, namely the existence of a minimum value for hmax (hmax0), corresponding to one atomic layer of the trapped gas atoms. As R approaches this regime, hmax becomes a constant value (hmax), and consequently, hmax/R transits into a ∼1/R dependence. This is illustrated in Figure 2c by the fit to the experimental hmax/R data with the function (hmax/R = c/R), where c (around 3 to 4 Å) is comparable to hmax0. This ∼1/R fit crosses the value corresponding to 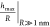Inline graphic (dotted line) around 1–2 nm, above which the universal scaling regime is valid and hmax/R becomes constant, given by eq 1.

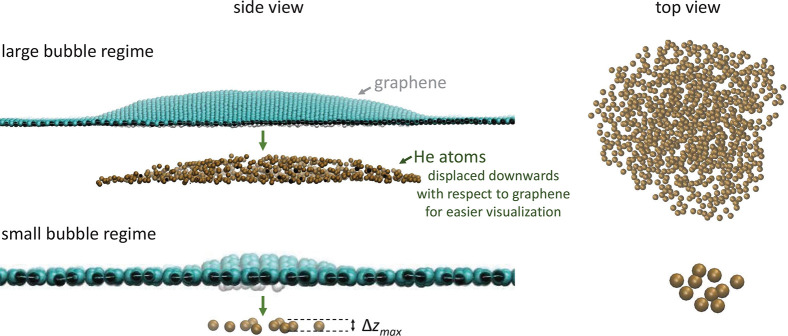
This behavior is well reproduced by our MD simulations of bubbles with a varying number of trapped atoms (from 800, with R of a few nm, down to a few atoms, with R below 1 nm—Figure 2). In particular, for the smallest bubbles with a small number of trapped atoms (of the order of 10), the monolayer-like configuration is clearly observed in our MD simulations (Figure 3), while for the larger bubbles, the trapped atoms are distributed over multiple layers of gas atoms (Figure 3). The significant spread in aspect ratio for a given radius (experimental data points in Figure 2) is likely due to a varying strength of the adhesion between graphene and the Pt surface (γGS) over the sample surface. Such nonhomogeneity can result from the varying (relative) orientation of the graphene and Pt lattices (the graphene layers grown on Pt are polycrystalline—Figure S8) as well as possible local variations in graphene–Pt adhesion due to the subtle graphene disorder observed in the STM and Raman data, discussed above. Although this possible effect of subtle disorder on the graphene–substrate adhesion may also play a role in the stability of the bubbles, it does not appear to be a dominant effect, since our MD simulations reproduce well the stability for Pt and instability for Cu without taking into account this disorder.

Figure 3.

Figure 3

Open in a new tab

Top and side view of examples of large and small He bubbles, simulated using MD. The He atoms are shown displaced downward, away from the graphene layer, for easier visualization. In the small-bubble regime, the He atoms are distributed in a monolayer-like configuration (i.e., without being on top of each other) but still with a significant out-of-plane motion amplitude (Δzmax).

Dependence on Trapped Element

Let us first consider the R ≫ 1 nm regime, where the universal scaling given by eq 1(5) applies, and thereby extract γ (given in Table 1) for each gas (He, Ne, and Ar). Although the values of 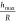Inline graphic for R ≫ 1 nm for He, Ne, and Ar are different, the spread over the various bubbles (reflected in a large standard deviation) blurs out these differences. Nevertheless, the data strongly suggest that this quantity does depend on the trapped element. Such a scenario can be understood as due to a variation in γ, that is, higher for Ne (γ ≈ 0.13 eV/Å2) and for He (∼0.08 eV/Å2) than for Ar (∼0.02 eV/Å2). Taking γGS = 0.25 eV/Å2 for graphene on Pt23 implies that γSb + γGb is of the order of γGS for Ar (giving γ = 0.02 eV/Å2) but significantly smaller for He and Ne. In other words, in the bubble configuration, the interaction (of vdW nature) of the gas atoms with the Pt surface or with the graphene layer appears to be more repulsive for Ne and He compared to Ar.

A similar trend is observed in the low-R regime, where the Ne bubbles clearly reach higher hmax values than for He and Ar bubbles (Figure 2) and hmax0 is also larger (although with a significant spread over various bubbles) for Ne than for He and Ar (Table 1). This is particularly noteworthy, as it does not follow the same trend as the vdW diameter (2rvdW), which increases from He, to Ne, to Ar (Table 1). Since, to a first approximation, one would expect the height of a bubble filled with a monolayer of noble gas atoms to scale with the vdW diameter of those atoms, other factors must also be playing a role, namely differences in atomic compressibility β and in out-of-plane motion of the noble gas elements. The effect of atomic compressibility is particularly obvious considering that while hmax is approximately equal to 2rvdW for He (2.9 and 2.86 Å, respectively) and only slightly higher for Ne (3.5 and 3.16 Å), it is significantly smaller for Ar (3.1 and 3.88 Å). This is indeed consistent with the fact that Ar is the most compressible of the three elements, followed by He and Ne (Table 1, from ref (22)). In addition to the compressibility, the differences in magnitude of the out-of-plane motion of the gas atoms are likely to also play a role, in particular, since as mentioned above for Ne, hmax0 is even larger than 2rvdW (3.5 and 3.16 Å, respectively). This is indeed consistent with our MD simulations. The average z-motion amplitude (averaged over time and over the trapped atoms) obtained from the MD simulations (Figure 3), for the smallest bubbles (⟨Δz⟩ in Table 1) is indeed significantly larger for Ne than for He and Ar. This out-of-plane motion forces hmax to be larger than the (compressed) vdW diameter (Figure 4b), that is, larger than that associated with a rigid atomic monolayer (Figure 4a), by an amount Δzmax that depends on γSb and γGb. In other words, the weaker the binding of the trapped atoms to the graphene layer and to the Pt surface, the more the gas atoms are allowed to move out-of-plane, and therefore, the more the sub-nm bubbles deviate from a static monolayer of (compressed) noble gas atoms.

Figure 4.

Figure 4

Open in a new tab

Schematics illustrating the relation between the bubble height in the small-bubble limit (h0) measured with STM, the vdW diameter of the trapped atoms (2rvdW), and the maximum out-of-plane motion amplitude (Δzmax): (a) When Δzmax ≈ 0, h0 ≈ 2rvdW and (b) when Δzmax > 0, h0 ≈ 2rvdW + Δzmax.

Extreme Strain and Pressure

The breakdown of the universal scaling, leading to extreme aspect ratios, is likely to be associated with other unusual physical properties in these subnanometer bubbles. Although studying such properties in detail is beyond the scope of this Letter, it is worthwhile discussing strain and pressure as examples. The tensile strain induced on graphene by the underlying trapped atoms can be estimated from our STM measurements as follows. From the STM topography of a bubble, one can determine the surface area of the graphene layer that wraps the three-dimensional bubble (Asurface) as well as the (projected) area of the base of the bubble (Aprojected). Asurface is the area of the strained graphene region, whereas Aprojected would be the area of that region if the bubble would not exist. The tensile strain can then be estimated as 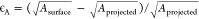Inline graphic. An accurate estimate requires smooth, low-noise, atomic-resolution STM micrographs of single bubbles. From selected high-quality micrographs of two He bubbles with R ≈ 1 nm, we obtain ϵA values of the order of 10%. More details are provided as Supporting Information. Regarding pressure, according to the general understanding of surface-induced pressure in solids, it scales with the ratio of surface area to the volume of the solid phase.24 For the bubbles under consideration here, as R decreases and the atoms inside the bubbles become more monolayer-like, the surface-to-volume ratio (∼Δz–1) increases dramatically, since Δz → 0. One can therefore expect the pressure to also increase dramatically in the limit of small R. Our MD calculations show exactly that (Figure 5), that is, a diverging behavior with decreasing R, reaching remarkably high values of up to ∼30 GPa. These values were obtained using the stress-tensor-based method,25 as recently applied to nanobubbles in graphene,6 with pressure being given by

graphic file with name nl1c02470_m006.jpg 2

where PvdW is the vdW pressure, Tr(σ) is the trace of the virial stress tensor, and Vb is the volume available to the gas atoms. We note that this method, based on the virial stress tensor, is more general and more appropriate in the present case compared to other methods based on membrane theory and plate theory. The latter methods are based on elasticity theory, which is valid in the large-bubble limit, but tends to overestimate the pressure for small bubbles.6 At such high pressures, at room temperature, these noble gases are expected to be in a solid phase or near their melting transition, which is around 10 GPa for He,26 5 GPa for Ne,27 and 1.5 GPa for Ar.28 Considering the pressures estimated here (Figure 5), one would then expect Ne and Ar to be in a solid-like phase, while He, with the highest melting transition (10 GPa), is expected to behave more liquid-like (possibly near a solid-like phase for R < 1 nm). Our MD simulations are indeed consistent with this expectation (cf. the videos provided as Supporting Information), showing rather stable ordered atomic arrangements for Ne (Videos V1 and V2) and Ar (V3 and V4) and more disordered and dynamic arrangements for He (V5 and V6).

Figure 5.

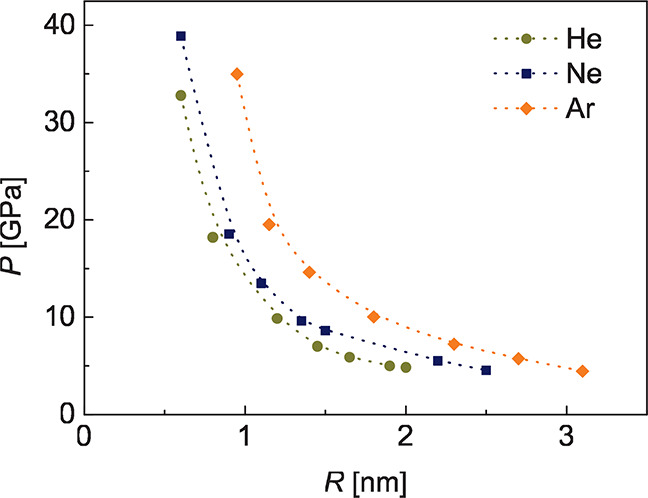
Figure 5

Open in a new tab

Pressure estimated from the MD simulations for He, Ne, and Ar bubbles in graphene/Pt(111), as a function of bubble radius. The lines are guides to the eye.

Stability on Pt versus Instability on Cu

As mentioned above, unlike for Pt, bubbles are not observed on Cu flat terraces. It appears that only the atoms that are trapped in defects (e.g., dips and terrace edges, as shown in Figure S1) are immobilized as intercalated species. The remainder is likely to escape via graphene defects (e.g., holes). This bubble instability for graphene on Cu is confirmed in our MD simulations (cf. the videos provided as Supporting Information): If a bubble configuration (similar to those in Pt—videos V7 and V8) is given as the initial state, the time evolution shows graphene peeling off the Cu surface, resulting in the dispersion of the trapped gas atoms (V9 and V10). This instability can be easily understood as due to the much weaker adhesion of graphene to Cu (γGS = 0.045 eV/Å229) compared to Pt (0.251 eV/Å223), that is, the Cu–graphene binding is too weak to sustain the high pressures associated with the bubbles. In order to assess if the gas–metal adhesion (γSb) also plays a role in this stability difference, we used DFT to calculate the adsorption energy and the adsorption distance of isolated He, Ne, and Ar atoms on Pt(111) and Cu(111) surfaces (Table S4). Although the adsorption energies are indeed larger for Pt than for Cu when comparing the gas elements one by one, it still does not explain the observed difference in stability. For example, the adsorption energies of Ar on Cu (for which bubbles are not stable) are larger than those of He on Pt (for which stable bubbles are observed). We therefore conclude that bubbles are not stable on flat Cu terraces due to the much weaker adhesion of graphene to Cu as compared to Pt.

To conclude, using ULE implantation of noble gas ions (He, Ne, and Ar), we produced nanobubbles on graphene with varying radius, from few nm down to subnanometer scales. These nanobubbles are stable for graphene on Pt but not for graphene on Cu. While the bubble aspect ratio behaves differently for the different elements, the universal scaling behavior (that was previously established for larger bubbles) breaks down in all three cases, for a bubble radius around 1 nm, as the bubble height approaches a minimum corresponding to about an atomic monolayer. We interpret the observed dependencies on the substrate and trapped element in terms of the adhesion energies between the three constituents: graphene, the substrate, and the trapped noble gas element. Moreover, these nanobubbles are found to induce high levels of strain (of the order of 10%) on the overlaying graphene. In addition to providing insight on the spatial distribution of the trapped atoms and its relation to the bubble morphology and stability, molecular dynamics calculations also allowed us to estimate the vdW pressure inside the bubbles, exceeding 30 GPa for the smallest bubbles. These remarkably high strains and pressures illustrate the unique characteristics of this subnanometer bubble regime (achievable using ultralow energy ion implantation) compared to the previously studied (larger) nanobubbles. These unique properties offer new opportunities, for example, to study physical states of matter and chemical reactions under high (vdW) pressure or electronic phenomena associated with strain-induced pseudomagnetic fields in graphene. Since the behavior reported here is largely determined by the adsorption energies between the three constituents (2D material, substrate, and trapped substance), one can expect similar behavior for other 2D materials (e.g., transition metal dichalcogenides such as MoS2), which expands even further the range of possible applications. In particular, since the bubble formation is based on ion implantation, our approach is compatible with virtually any implanted element, 2D material, and substrate.

Acknowledgments

This work was funded by KU Leuven and FWO Vlaanderen. M.N.N. acknowledges funding from the EU Horizon 2020 Framework (MagDirac project, ID:796940). The authors also acknowledge funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement GrapheneCore3 881603. E.H.Å acknowledges funding from Austrian Science Fund (FWF) project number M2595. The authors also thank Peter Walke for the support with the Raman spectroscopy measurements. The work was carried out in part using the CalcUA core facility of the Universiteit Antwerpen (UA).

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.nanolett.1c02470.

  • Ne atoms in small bubble on Pt (bottom view) (MP4)

  • Ne atoms in large bubble on Pt (bottom view) (MP4)

  • Ar atoms in small bubble on Pt (bottom view) (MP4)

  • Ar atoms in large bubble on Pt (bottom view) (MP4)

  • He atoms in small bubble on Pt (bottom view) (MP4)

  • Small He bubble on Pt (MP4)

  • He atoms in large bubble on Pt (bottom view) (MP4)

  • Large He bubble on Pt (MP4)

  • Small He bubble on Cu (MP4)

  • Large He bubble on Cu (MP4)

  • (1) Methods: details on the growth of graphene on Cu and Pt (by chemical vapor deposition), the ultralow energy ion implantation, the experimental characterization (scanning tunneling microscopy, Raman spectroscopy, low-energy electron diffraction), and computational methods (molecular dynamics simulations and density functional theory calculations); (2) additional results from calculations and from experimental characterization, with accompanying references.30−63 (PDF)

Author Contributions

†† R.V. and P.-C.L. contributed equally to this work

The authors declare no competing financial interest.

Supplementary Material

nl1c02470_si_001.mp4 (3.7MB, mp4)
nl1c02470_si_002.mp4 (1.9MB, mp4)
nl1c02470_si_003.mp4 (3.7MB, mp4)
nl1c02470_si_004.mp4 (3.4MB, mp4)
nl1c02470_si_005.mp4 (3.7MB, mp4)
nl1c02470_si_007.mp4 (3.3MB, mp4)
nl1c02470_si_006.mp4 (7.6MB, mp4)
nl1c02470_si_008.mp4 (6.6MB, mp4)
nl1c02470_si_009.mp4 (6.7MB, mp4)
nl1c02470_si_010.mp4 (8.1MB, mp4)
nl1c02470_si_011.pdf (13.8MB, pdf)

References

  1. Lee C.; Wei X.; Kysar J. W.; Hone J. Measurement of the Elastic Properties and Intrinsic Strength of Monolayer Graphene. Science 2008, 321, 385–388. 10.1126/science.1157996. [DOI] [PubMed] [Google Scholar]
  2. Lee G.-H.; Cooper R. C.; An S. J.; Lee S.; Van Der Zande A.; Petrone N.; Hammerberg A. G.; Lee C.; Crawford B.; Oliver W.; Kysar J. W.; Hone J. High-Strength Chemical-Vapor–Deposited Graphene and Grain Boundaries. Science 2013, 340, 1073–1076. 10.1126/science.1235126. [DOI] [PubMed] [Google Scholar]
  3. Zamborlini G.; Imam M.; Patera L. L.; Mentes T. O.; Stojic N.; Africh C.; Sala A.; Binggeli N.; Comelli G.; Locatelli A. Nanobubbles at GPa Pressure Under Graphene. Nano Lett. 2015, 15, 6162–6169. 10.1021/acs.nanolett.5b02475. [DOI] [PubMed] [Google Scholar]
  4. Larciprete R.; Colonna S.; Ronci F.; Flammini R.; Lacovig P.; Apostol N.; Politano A.; Feulner P.; Menzel D.; Lizzit S. Self-Assembly of Graphene Nanoblisters Sealed to a Bare Metal Surface. Nano Lett. 2016, 16, 1808–1817. 10.1021/acs.nanolett.5b04849. [DOI] [PubMed] [Google Scholar]
  5. Khestanova E.; Guinea F.; Fumagalli L.; Geim A.; Grigorieva I. Universal Shape and Pressure Inside Bubbles Appearing in van der Waals Heterostructures. Nat. Commun. 2016, 7, 12587. 10.1038/ncomms12587. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Ghorbanfekr-Kalashami H.; Vasu K.; Nair R.; Peeters F. M.; Neek-Amal M. Dependence of the Shape of Graphene Nanobubbles on Trapped Substance. Nat. Commun. 2017, 8, 15844. 10.1038/ncomms15844. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Qi Z.; Kitt A. L.; Park H. S.; Pereira V. M.; Campbell D. K.; Castro Neto A. H. Pseudomagnetic Fields in Graphene Nanobubbles of Constrained Geometry: A molecular Dynamics Study. Phys. Rev. B: Condens. Matter Mater. Phys. 2014, 90, 125419. 10.1103/PhysRevB.90.125419. [DOI] [Google Scholar]
  8. Levy N.; Burke S.; Meaker K.; Panlasigui M.; Zettl A.; Guinea F.; Neto A. C.; Crommie M. F. Strain-Induced Pseudo–Magnetic Fields Greater than 300 T in Graphene Nanobubbles. Science 2010, 329, 544–547. 10.1126/science.1191700. [DOI] [PubMed] [Google Scholar]
  9. Jia P.; Chen W.; Qiao J.; Zhang M.; Zheng X.; Xue Z.; Liang R.; Tian C.; He L.; Di Z.; Wang X. Programmable Graphene Nanobubbles with Three-Fold Symmetric Pseudo-Magnetic Fields. Nat. Commun. 2019, 10, 3127. 10.1038/s41467-019-11038-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Lim C. H. Y. X.; Nesladek M.; Loh K. P. Observing High-Pressure Chemistry in Graphene Bubbles. Angew. Chem., Int. Ed. 2014, 53, 215–219. 10.1002/anie.201308682. [DOI] [PubMed] [Google Scholar]
  11. Vasu K.; Prestat E.; Abraham J.; Dix J.; Kashtiban R.; Beheshtian J.; Sloan J.; Carbone P.; Neek-Amal M.; Haigh S.; Geim A. K.; Nair R. R. van der Waals Pressure and its Effect on Trapped Interlayer Molecules. Nat. Commun. 2016, 7, 12168. 10.1038/ncomms12168. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Carmesin C.; Lorke M.; Florian M.; Erben D.; Schulz A.; Wehling T. O.; Jahnke F. Quantum-Dot-Like States in Molybdenum Disulfide Nanostructures due to the Interplay of Local Surface Wrinkling, Strain, and Dielectric Confinement. Nano Lett. 2019, 19, 3182–3186. 10.1021/acs.nanolett.9b00641. [DOI] [PubMed] [Google Scholar]
  13. Wang Y.-T.; Liu W.; Li Z.-P.; Yu S.; Ke Z.-J.; Meng Y.; Tang J.-S.; Li C.-F.; Guo G.-C.. A bubble-induced ultrastable and robust single-photon emitter in hexagonal boron nitride. 2019, arXiv:1906.00493. arXiv preprint. https://arxiv.org/abs/1906.00493 (accessed July 23, 2021).
  14. Herbig C.; Åhlgren E. H.; Schröder U. A.; Martinez-Galera A. J.; Arman M. A.; Kotakoski J.; Knudsen J.; Krasheninnikov A. V.; Michely T. Xe Irradiation of Graphene on Ir (111): From Trapping to Blistering. Phys. Rev. B: Condens. Matter Mater. Phys. 2015, 92, 085429. 10.1103/PhysRevB.92.085429. [DOI] [Google Scholar]
  15. Kim H. W.; Ko W.; Ku J.; Jeon I.; Kim D.; Kwon H.; Oh Y.; Ryu S.; Kuk Y.; Hwang S. W.; Suh H. Nanoscale Control of Phonon Excitations in Graphene. Nat. Commun. 2015, 6, 7528. 10.1038/ncomms8528. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Verguts K.; Defossez Y.; Leonhardt A.; De Messemaeker J.; Schouteden K.; Van Haesendonck C.; Huyghebaert C.; De Gendt S.; Brems S. Growth of Millimeter-Sized Graphene Single Crystals on Al2O3(0001)/Pt(111) Template Wafers Using Chemical Vapor Deposition. ECS J. Solid State Sci. Technol. 2018, 7, M195. 10.1149/2.0101812jss. [DOI] [Google Scholar]
  17. Verguts K.; Vrancken N.; Vermeulen B.; Huyghebaert C.; Terryn H.; Brems S.; De Gendt S. Single-Layer Graphene Synthesis on a Al2O3(0001)/Cu(111) Template Using Chemical Vapor Deposition. ECS J. Solid State Sci. Technol. 2016, 5, Q3060. 10.1149/2.0121611jss. [DOI] [Google Scholar]
  18. Bangert U.; Pierce W.; Kepaptsoglou D.; Ramasse Q.; Zan R.; Gass M.; Van den Berg J.; Boothroyd C.; Amani J.; Hofsäss H. Ion Implantation of Graphene - Toward IC Compatible Technologies. Nano Lett. 2013, 13, 4902–4907. 10.1021/nl402812y. [DOI] [PubMed] [Google Scholar]
  19. Kepaptsoglou D.; Hardcastle T. P.; Seabourne C. R.; Bangert U.; Zan R.; Amani J. A.; Hofsäss H.; Nicholls R. J.; Brydson R. M. D.; Scott A. J.; Ramasse Q. M. Electronic Structure Modification of Ion Implanted Graphene: The Spectroscopic Signatures of p-and n-Type Doping. ACS Nano 2015, 9, 11398–11407. 10.1021/acsnano.5b05305. [DOI] [PubMed] [Google Scholar]
  20. Willke P.; Amani J. A.; Sinterhauf A.; Thakur S.; Kotzott T.; Druga T.; Weikert S.; Maiti K.; Hofsäss H.; Wenderoth M. Doping of Graphene by Low-Energy Ion Beam Implantation: Structural, Electronic, and Transport Properties. Nano Lett. 2015, 15, 5110–5115. 10.1021/acs.nanolett.5b01280. [DOI] [PubMed] [Google Scholar]
  21. Vogt J.; Alvarez S. van der Waals Radii of Noble Gases. Inorg. Chem. 2014, 53, 9260–9266. 10.1021/ic501364h. [DOI] [PubMed] [Google Scholar]
  22. Tandon H.; Chakraborty T.; Suhag V. A Model of Atomic Compressibility and its Application in QSAR Domain for Toxicological Property Prediction. J. Mol. Model. 2019, 25, 303. 10.1007/s00894-019-4199-9. [DOI] [PubMed] [Google Scholar]
  23. Torres J.; Zhu Y.; Liu P.; Lim S. C.; Yun M. Adhesion Energies of 2D Graphene and MoS2 to Silicon and Metal Substrates. Phys. Status Solidi A 2018, 215, 1700512. 10.1002/pssa.201700512. [DOI] [Google Scholar]
  24. Weissmüller J.; Cahn J. Mean Stresses in Microstructures Due to Interface Stresses: A Generalization of a Capillary Equation for Solids. Acta Mater. 1997, 45, 1899–1906. 10.1016/S1359-6454(96)00314-X. [DOI] [Google Scholar]
  25. Tsai D. The Virial Theorem and Stress Calculation in Molecular Dynamics. J. Chem. Phys. 1979, 70, 1375–1382. 10.1063/1.437577. [DOI] [Google Scholar]
  26. Santamaría-Pérez D.; Mukherjee G. D.; Schwager B.; Boehler R. High-Pressure Melting Curve of Helium and Neon: Deviations from Corresponding States Theory. Phys. Rev. B: Condens. Matter Mater. Phys. 2010, 81, 214101. 10.1103/PhysRevB.81.214101. [DOI] [Google Scholar]
  27. Vos W.; Schouten J.; Young D.; Ross M. The Melting Curve of Neon at High Pressure. J. Chem. Phys. 1991, 94, 3835–3838. 10.1063/1.460683. [DOI] [Google Scholar]
  28. Datchi F.; Loubeyre P.; LeToullec R. Melting Curves of Hydrogen, H2O, Helium and Argon at High Pressure. Koatsuryoku no Kagaku to Gijutsu 1998, 7, 778–780. 10.4131/jshpreview.7.778. [DOI] [Google Scholar]
  29. Yoon T.; Shin W. C.; Kim T. Y.; Mun J. H.; Kim T.-S.; Cho B. J. Direct Measurement of Adhesion Energy of Monolayer Graphene As-Grown on Copper and its Application to Renewable Transfer Process. Nano Lett. 2012, 12, 1448–1452. 10.1021/nl204123h. [DOI] [PubMed] [Google Scholar]
  30. Stuart S. J.; Tutein A. B.; Harrison J. A. A Reactive Potential for Hydrocarbons with Intermolecular Interactions. J. Chem. Phys. 2000, 112, 6472–6486. 10.1063/1.481208. [DOI] [Google Scholar]
  31. Daw M. S.; Baskes M. I. Semiempirical, Quantum Mechanical Calculation of Hydrogen Embrittlement in Metals. Phys. Rev. Lett. 1983, 50, 1285–1288. 10.1103/PhysRevLett.50.1285. [DOI] [Google Scholar]
  32. Hippler H.; Troe J.; Wendelken H. Collisional Deactivation of Vibrationally Highly Excited Polyatomic Molecules. II. Direct Observations for Excited Toluene. J. Chem. Phys. 1983, 78, 6709–6717. 10.1063/1.444670. [DOI] [Google Scholar]
  33. Girifalco L. A.; Hodak M.; Lee R. S. Carbon Nanotubes, Buckyballs, Ropes, and a Universal Graphitic Potential. Phys. Rev. B: Condens. Matter Mater. Phys. 2000, 62, 13104. 10.1103/PhysRevB.62.13104. [DOI] [Google Scholar]
  34. Halicioǧlu T.; Pound G. Calculation of Potential Energy Parameters form Crystalline State Properties. Phys. Status Solidi 1975, 30, 619–623. 10.1002/pssa.2210300223. [DOI] [Google Scholar]
  35. Kong C. L. Combining Rules for Intermolecular Potential Parameters. II. Rules for the Lennard-Jones (12–6) Potential and the Morse Potential. J. Chem. Phys. 1973, 59, 2464–2467. 10.1063/1.1680358. [DOI] [Google Scholar]
  36. Plimpton S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. 10.1006/jcph.1995.1039. [DOI] [Google Scholar]
  37. Delley B. From Molecules to Solids with the DMol 3 Approach. J. Chem. Phys. 2000, 113, 7756–7764. 10.1063/1.1316015. [DOI] [Google Scholar]
  38. Perdew J. P.; Burke K.; Ernzerhof M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
  39. Bučko T.; Lebègue S.; Hafner J.; Angyan J. G. Tkatchenko-Scheffler van der Waals Correction Method with and Without Self-Consistent Screening Applied to Solids. Phys. Rev. B: Condens. Matter Mater. Phys. 2013, 87, 064110. 10.1103/PhysRevB.87.064110. [DOI] [Google Scholar]
  40. Ferrari A. C. Raman Spectroscopy of Graphene and Graphite: Disorder, Electron–Phonon Coupling, Doping and Nonadiabatic Effects. Solid State Commun. 2007, 143, 47–57. 10.1016/j.ssc.2007.03.052. [DOI] [Google Scholar]
  41. Lucchese M. M.; Stavale F.; Ferreira E. M.; Vilani C.; Moutinho M. V. d. O.; Capaz R. B.; Achete C. A.; Jorio A. Quantifying Ion-Induced Defects and Raman Relaxation Length in Graphene. Carbon 2010, 48, 1592–1597. 10.1016/j.carbon.2009.12.057. [DOI] [Google Scholar]
  42. Cançado L. G.; Jorio A.; Ferreira E. M.; Stavale F.; Achete C. A.; Capaz R. B.; Moutinho M. V. d. O.; Lombardo A.; Kulmala T.; Ferrari A. C. Quantifying Defects in Graphene via Raman Spectroscopy at Different Excitation Energies. Nano Lett. 2011, 11, 3190–3196. 10.1021/nl201432g. [DOI] [PubMed] [Google Scholar]
  43. Cress C. D.; Schmucker S. W.; Friedman A. L.; Dev P.; Culbertson J. C.; Lyding J. W.; Robinson J. T. Nitrogen-Doped Graphene and Twisted Bilayer Graphene via Hyperthermal Ion Implantation with Depth Control. ACS Nano 2016, 10, 3714–3722. 10.1021/acsnano.6b00252. [DOI] [PubMed] [Google Scholar]
  44. Mooradian A. Photoluminescence of Metals. Phys. Rev. Lett. 1969, 22, 185–187. 10.1103/PhysRevLett.22.185. [DOI] [Google Scholar]
  45. Zhou Q.; Coh S.; Cohen M. L.; Louie S. G.; Zettl A. Imprint of Transition Metal d Orbitals on a Graphene Dirac Cone. Phys. Rev. B: Condens. Matter Mater. Phys. 2013, 88, 235431. 10.1103/PhysRevB.88.235431. [DOI] [Google Scholar]
  46. Cazzanelli E.; Caruso T.; Castriota M.; Marino A.; Politano A.; Chiarello G.; Giarola M.; Mariotto G. Spectroscopic Characterization of Graphene Films Grown on Pt (111) Surface by Chemical Vapor Deposition of Ethylene. J. Raman Spectrosc. 2013, 44, 1393–1397. 10.1002/jrs.4285. [DOI] [Google Scholar]
  47. Bruna M.; Ott A. K.; Ijas M.; Yoon D.; Sassi U.; Ferrari A. C. Doping Dependence of the Raman Spectrum of Defected Graphene. ACS Nano 2014, 8, 7432–7441. 10.1021/nn502676g. [DOI] [PubMed] [Google Scholar]
  48. Hernández-Rodríguez I.; García J. M.; Martín-Gago J. A.; de Andrés P. L.; Méndez J. Graphene Growth on Pt(111) and Au(111) Using a MBE Carbon Solid-Source. Diamond Relat. Mater. 2015, 57, 58–62. 10.1016/j.diamond.2015.03.004. [DOI] [Google Scholar]; 25th International Conference on Diamond and Carbon Materials – DCM 2014.
  49. Martínez-Galera A. J.; Gómez-Rodríguez J. M. Surface Diffusion of Simple Organic Molecules on Graphene on Pt(111). J. Phys. Chem. C 2011, 115, 23036–23042. 10.1021/jp208026u. [DOI] [Google Scholar]
  50. Berendsen H. J.; Postma J. v.; van Gunsteren W. F.; DiNola A.; Haak J. R. Molecular Dynamics with Coupling to an External Bath. J. Chem. Phys. 1984, 81, 3684–3690. 10.1063/1.448118. [DOI] [Google Scholar]
  51. Brenner D. W.; Shenderova O. A.; Harrison J. A.; Stuart S. J.; Ni B.; Sinnott S. B. A Second-Generation Reactive Empirical Bond Order (REBO) Potential Energy Expression for Hydrocarbons. J. Phys.: Condens. Matter 2002, 14, 783–802. 10.1088/0953-8984/14/4/312. [DOI] [Google Scholar]
  52. Ziegler J.; Biersack J. The Stopping and Range of Ions in Matter. Treatise on Heavy-Ion Science 1985, 93–129. 10.1007/978-1-4615-8103-1_3. [DOI] [Google Scholar]
  53. Teweldebrhan D.; Balandin A. A. Modification of Graphene Properties due to Electron-Beam Irradiation. Appl. Phys. Lett. 2009, 94, 013101. 10.1063/1.3062851. [DOI] [Google Scholar]
  54. Iqbal M.; Kumar Singh A.; Iqbal M.; Seo S.; Eom J. Effect of E-Beam Irradiation on Graphene Layer Grown by Chemical Vapor Deposition. J. Appl. Phys. 2012, 111, 084307. 10.1063/1.4704197. [DOI] [Google Scholar]
  55. Gao A.; Lee C. J.; Bijkerk F. Graphene Defect Formation by Extreme Ultraviolet Generated Photoelectrons. J. Appl. Phys. 2014, 116, 054312. 10.1063/1.4892485. [DOI] [Google Scholar]
  56. Krauss B.; Lohmann T.; Chae D.-H.; Haluska M.; von Klitzing K.; Smet J. H. Laser-Induced Disassembly of a Graphene Single Crystal into a Nanocrystalline Network. Phys. Rev. B: Condens. Matter Mater. Phys. 2009, 79, 165428. 10.1103/PhysRevB.79.165428. [DOI] [Google Scholar]
  57. Kudin K. N.; Scuseria G. E.; Yakobson B. I. C2F, BN, and C Nanoshell Elasticity from ab initio Computations. Phys. Rev. B: Condens. Matter Mater. Phys. 2001, 64, 235406. 10.1103/PhysRevB.64.235406. [DOI] [Google Scholar]
  58. Eggert J.; Brygoo S.; Loubeyre P.; McWilliams R. S.; Celliers P. M.; Hicks D. G.; Boehly T. R.; Jeanloz R.; Collins G. W. Hugoniot Data for Helium in the Ionization Regime. Phys. Rev. Lett. 2008, 100, 124503. 10.1103/PhysRevLett.100.124503. [DOI] [PubMed] [Google Scholar]
  59. Hemley R. J.; Zha C. S.; Jephcoat A. P.; Mao H. K.; Finger L. W.; Cox D. E. X-Ray Diffraction and Equation of State of Solid Neon to 110 GPa. Phys. Rev. B: Condens. Matter Mater. Phys. 1989, 39, 11820. 10.1103/PhysRevB.39.11820. [DOI] [PubMed] [Google Scholar]
  60. Shimizu H.; Tashiro H.; Kume T.; Sasaki S. High-Pressure Elastic Properties of Solid Argon to 70 GPa. Phys. Rev. Lett. 2001, 86, 4568. 10.1103/PhysRevLett.86.4568. [DOI] [PubMed] [Google Scholar]
  61. Nosé S. A Unified Formulation of the Constant Temperature Molecular Dynamics Methods. J. Chem. Phys. 1984, 81, 511–519. 10.1063/1.447334. [DOI] [Google Scholar]
  62. Hoover W. G. Canonical Dynamics: Equilibrium Phase-Space Distributions. Phys. Rev. A: At., Mol., Opt. Phys. 1985, 31, 1695. 10.1103/PhysRevA.31.1695. [DOI] [PubMed] [Google Scholar]
  63. Verlet L. Computer “Experiments” on Classical Fluids. I. Thermodynamical Properties of Lennard-Jones Molecules. Phys. Rev. 1967, 159, 98. 10.1103/PhysRev.159.98. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

nl1c02470_si_001.mp4 (3.7MB, mp4)
nl1c02470_si_002.mp4 (1.9MB, mp4)
nl1c02470_si_003.mp4 (3.7MB, mp4)
nl1c02470_si_004.mp4 (3.4MB, mp4)
nl1c02470_si_005.mp4 (3.7MB, mp4)
nl1c02470_si_007.mp4 (3.3MB, mp4)
nl1c02470_si_006.mp4 (7.6MB, mp4)
nl1c02470_si_008.mp4 (6.6MB, mp4)
nl1c02470_si_009.mp4 (6.7MB, mp4)
nl1c02470_si_010.mp4 (8.1MB, mp4)
nl1c02470_si_011.pdf (13.8MB, pdf)

Articles from Nano Letters are provided here courtesy of American Chemical Society

RESOURCES