Micromagnetic Tomography for Paleomagnetism and Rock‐Magnetism

Abstract

Our understanding of the past behavior of the geomagnetic field arises from magnetic signals stored in geological materials, e.g., (volcanic) rocks. Bulk rock samples, however, often contain magnetic grains that differ in chemistry, size, and shape; some of them record the Earth's magnetic field well, others are unreliable. The presence of a small amount of adverse behaved magnetic grains in a sample may already obscure important information on the past state of the geomagnetic field. Recently it was shown that it is possible to determine magnetizations of individual grains in a sample by combining X‐ray computed tomography and magnetic surface scanning measurements. Here we establish this new Micromagnetic Tomography (MMT) technique and make it suitable for use with different magnetic scanning techniques, and for both synthetic and natural samples. We acquired reliable magnetic directions by selecting subsets of grains in a synthetic sample, and we obtained rock‐magnetic information of individual grains in a volcanic sample. This illustrates that MMT opens up entirely new venues of paleomagnetic and rock‐magnetic research. MMT's unique ability to determine the magnetization of individual grains in a nondestructive way allows for a systematic analysis of how geological materials record and retain information on the past state of the Earth's magnetic field. Moreover, by interpreting only the contributions of known magnetically well‐behaved grains in a sample, MMT has the potential to unlock paleomagnetic information from even the most complex, crucial, or valuable recorders that current methods are unable to recover.

Key Points

• Micromagnetic Tomography enables determining, selecting, and interpreting magnetizations of individual grains in a sample

• We obtained magnetic directions and rock‐magnetic information from subsets of grains in both a synthetic and a natural sample

• Micromagnetic Tomography has the potential to unlock magnetic information from even the most complex recorders that currently goes obscured

1. Introduction

To understand the behavior of the Earth's magnetic field, and possibly even predict its future behavior, it is paramount to understand its past. Our understanding of the behavior of the geomagnetic field arises from magnetic signals stored in geological and archeological materials. They acquire a magnetization when they cool in the Earth's magnetic field, and retain that magnetization over (geological) timescales. Igneous rocks, e.g., lavas, are the only recorders of the direction and the intensity of the field that are available throughout geologic history and all over the globe. Since lavas take snapshots of the state of the Earth's magnetic field for their location and point in time when they cool, frequently erupting volcanic regions with well‐dated volcanic products are invaluable archives of past variations in the Earth's magnetic field (e.g., Cromwell et al., ²⁰¹⁵; Greve et al., ²⁰¹⁷; de Groot et al., ²⁰¹³).

When a volcano erupts and lava cools on its flanks the lava solidifies to form extrusive igneous rocks, often of basaltic composition. A small, but significant, portion of the minerals that together constitute these basalts has magnetic properties. Lavas are often regarded to be excellent paleomagnetic recorders, but over the past years evidence piled up that their magnetic signal is often compromised. This has been known for a long time for reconstructions of variations in field strength. Viscous changes in the magnetic signal of natural rocks (e.g., de Groot, Fabian, et al., ²⁰¹⁴; Shaar et al., ²⁰¹¹) or thermochemical changes during laboratory experiments (e.g., Fabian, ²⁰⁰⁹; Shcherbakov et al., ²⁰¹⁹) frequently hamper paleointensity experiments (Tauxe & Yamazaki, 2015). But even obtaining a paleomagnetic direction from volcanic samples is not always straightforward, as illustrated by a recent reappraisal of the paleomagnetic signal stored in a stack of lava flows from Steens Mountain (Coe et al., 2014), that falsified a previous interpretation of a very rapid change in the direction of the Earth's magnetic field during a geomagnetic polarity reversal (Prévot et al., 1985).

Almost all experiments to determine the past state of the Earth's magnetic field from rocks use bulk samples (usually $\sim$10 cc) and measure their magnetic moment after series of laboratory treatments. Lavas consist of mixtures of different iron‐oxides that vary in size, shape, and chemistry. These iron‐oxide grains are the actual magnetic recorders in the samples. Some of these grains record the Earth's magnetic field well; others may not be able to provide reliable information on its past state. When measuring a typical paleomagnetic sample, the magnetic moments of millions of grains are measured simultaneously and result in one magnetic moment for the entire sample. A small amount of adverse behaved magnetic grains in a sample already hampers any classical experiment to obtain paleointensities. Therefore, these experiments often fail and success rates as low as 10%–20% are common (Valet, 2003; Tauxe & Yamazaki, ²⁰¹⁵). This implies that for 80%–90% of all lavas vital information on paleointensities is lost before it can be uncovered.

The iron‐oxide grains in lava acquire a magnetization that is proportional to the ambient magnetic field during cooling; such magnetizations are referred to as thermoremanent magnetizations (TRMs). The magnetic properties of iron‐oxide grains vary dramatically due to differences in grain size, shape, chemistry, and thermal history as summarized by Dunlop and Özdemir (1997). The magnetic behavior of very small single domain iron‐oxides (30–60 nm) is described by Néel's theory on thermoremanent magnetizations in single‐domain ferromagnetic minerals (Néel, 1949, ¹⁹⁵⁵). These grains are magnetically well‐behaved; if a sample would consist of only such small grains it would be relatively straightforward to obtain a reliable estimate of both the paleodirection and paleointensity of the Earth's magnetic field using classical paleomagnetic techniques. Unfortunately, iron‐oxides in naturally occurring lavas are generally much larger (up to $>$50 μm). Not only do these multi‐domain grains violate Néel's theory, but they also often violate Thellier's laws of reciprocity, independence, and additivity (e.g., Coe, ¹⁹⁶⁷; Dunlop, ²⁰¹¹; Fabian, ²⁰⁰⁰, ²⁰⁰¹; Shcherbakova et al., ²⁰⁰⁰; Tauxe & Yamazaki, ²⁰¹⁵; Thellier & Thellier, ¹⁹⁵⁹). Moreover, these multi‐domain grains may be prone to unstable magnetizations over time caused by e.g., viscous reordering of magnetic domains (de Groot, Fabian, et al., ²⁰¹⁴), or time and temperature‐dependent cation reordering (Bowles et al., 2013; Bowles & Jackson, ²⁰¹⁶). In contrast to Néel's theory for single domain grains, there currently is no comprehensive, fundamental theory for the processes governing the acquisition and preservation of magnetic signals in multi‐domain grains. Their magnetic behavior is thus still enigmatic, although they make up the vast majority of the remanence carrying grains in igneous rocks.

If we would be able to determine the magnetic moments of individual mineral grains inside a natural sample in a non‐destructive way, we could determine which naturally occurring iron‐oxide grains record the Earth's magnetic field well, and which are unreliable. This would enable us to select and consider only the magnetic contributions of known well‐behaved magnetic grains, and reject the contributions of others. Thereby we could fully unlock the paleomagnetic information stored in all sorts of geological materials, even if large amounts of adverse behaved magnetic minerals are present in the sample. This will provide indispensable data to understand the behavior of the geomagnetic field on decadal to centennial time scales, and possibly enables predictions of its future behavior.

Information about the magnetic state of individual grains in a sample can theoretically be obtained from scans of magnetic anomalies on the surface of a sample if the spatial resolution permits. The rock‐magnetic interpretation of these magnetic surface scans, however, is notoriously difficult. The classical potential inversion problem (Kellogg, 1929) states that it is impossible to obtain unique information on the distribution of magnetic sources (i.e., our grains) within a body (i.e., our sample), based on observations of the magnetization outside this body alone. Additional information or assumptions are necessary to characterize the magnetic sources (Lima & Weiss, 2009; Lima et al., ²⁰¹³). Currently, the interpretation of these magnetic maps is often done by an upward continuation of the magnetic measurements: the magnetic signal for the entire sample or region is inferred by calculating the resulting magnetic moment further away from the sample (Blakely, 1995; Fu et al., ²⁰²⁰; Lima & Weiss, ²⁰⁰⁹, ²⁰¹⁶; Lima et al., ²⁰¹⁴). This implicitly averages the magnetic contributions present in the region of interest, without the possibility to assess or consider the quality of individual grains as paleomagnetic recorders.

We recently overcame the non‐uniqueness of the classical potential inversion problem by adding the results of an X‐ray computed tomography (microCT) scan to the results of scanning magnetometry (de Groot et al., ²⁰¹⁸). The microCT scan determines the exact locations, sizes, and shapes of the iron‐oxides grains in a sample, which ensures that our inversion routine can now only attribute magnetizations from the surface magnetometry to the magnetic grains in our sample. The additional microCT information, therefore, enables a unique inversion of the information produced by scanning magnetometry without the necessity of any further assumptions (Fabian & de Groot, 2019). With this newly developed technique now known as Micromagnetic Tomography (MMT) the individual magnetic moments of 20 grains inside a synthetic sample were successfully determined (de Groot et al., ²⁰¹⁸). The synthetic sample used in this study, however, was optimized for success: its concentration of magnetic grains was one to two orders of magnitude lower compared to natural samples, and pure magnetite grains with a well‐defined suite of grain sizes were used—in contrast to the large variation in grain sizes and chemistry of naturally occurring iron‐oxides. Given these characteristics of the synthetic sample and the amount of grains for which magnetic moments were determined, the MMT study by de Groot et al. (2018) is fore‐mostly a proof‐of‐concept. Here we build on this proof‐of‐concept and (a) show that the MMT technique is universally applicable by using different magnetic scanning techniques, (b) up‐scale the technique to be useful for natural (volcanic) samples, (c) show that it is possible to acquire magnetic directions by selecting subsets of grains present in a sample using MMT, and (d) acquire a rock‐magnetic characterization of grains in a volcanic sample from MMT. This firmly establishes MMT as a new paleomagnetic and rock‐magnetic technique that is useful to unlock information from samples with complex magnetic behavior that current paleomagnetic and rock‐magnetic methods are unable to recover.

2. Micromagnetic Tomography

The MMT technique determines the magnetic moments of individual grains in a sample by inverting a two‐dimensional magnetic surface scan of the sample based on the known locations and shapes of the iron‐oxide grains as determined by a microCT scan of the sample. The input for any MMT experiment is thus (a) a magnetic surface scan and (b) a microCT characterization of the sample (Figure 1). These two data sets must first be co‐registered into a common spatial coordinate system before a mathematical inversion of the magnetic surface scan constrained by the microCT data can produce the magnetic moments of the grains. The accuracy of the inversion results can then be assessed by determining the residuals left by the inversion.

Figure 1.

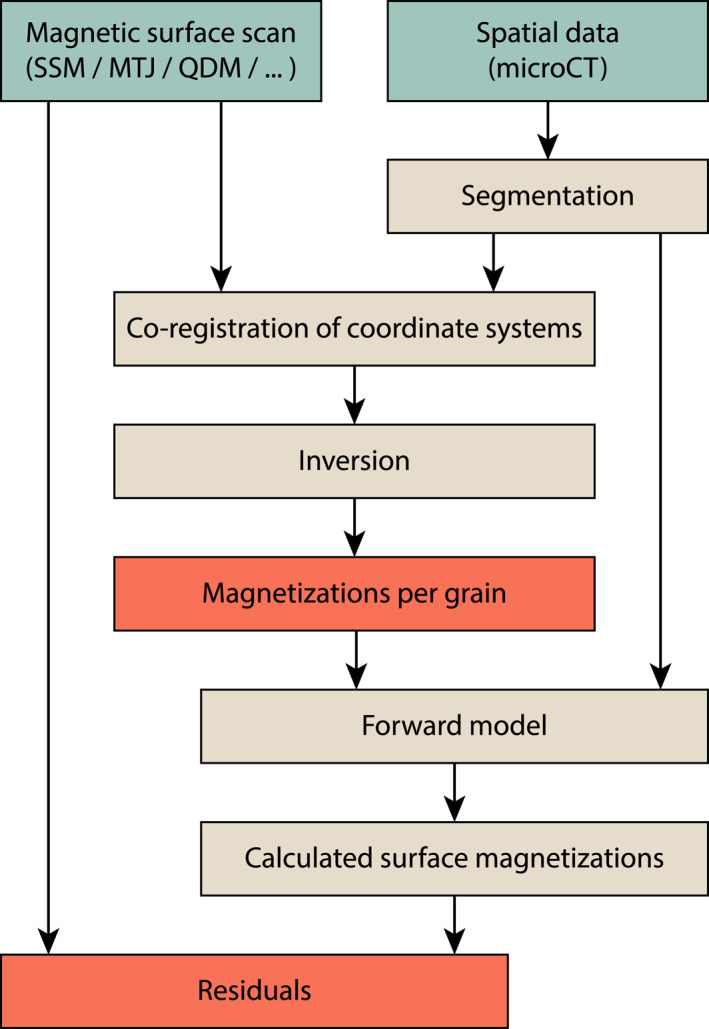
Workflow of Micromagnetic Tomography experiments. The input (measurements) is in the green boxes; computational steps are in the tan boxes and the output is in the red boxes.

2.1. MicroCT Analysis

The locations, sizes, and shapes of the iron‐oxide grains in a sample are determined using a microCT scan. This technique produces a three‐dimensional image of the X‐ray attenuation contrast in a sample, which is often interpreted in terms of variations in density in the sample (Jussiani & Appoloni, 2015; Madonna et al., ²⁰¹²; Sakellariou et al., ²⁰⁰⁴). The densities of iron‐oxides (e.g., magnetite: 5.2, hematite: 5.3, ülvospinel: 4.8, and ilmenite: $4.8\times 10^3$ kg/${\mathrm{m}}^3$) are generally 1.4 to 2 times larger than the densities of other common minerals in basalt (e.g., plagioclases: $2.6-2.8$, and pyroxenes $3.2-3.9\times 10^3$ kg/${\mathrm{m}}^3$), although the heavier olivines ($3.2-4.4\times 10^3$ kg/${\mathrm{m}}^3$), have a less profound difference (density data from www.mindat.org). Because of these large density differences between iron‐oxide minerals and other minerals and/or (synthetic) matrices present in a sample, the attenuation contrast in microCT scans generally allows to precisely locate all iron‐oxides with volumes above the voxel limit, and also to estimate their shape and volume within the limits of the voxel representation.

When using microCT data it is up to the interpreter to make selections in the attenuation contrast spectrum in the sample for the segmentation of individual iron‐oxide grains by setting a density threshold above which voxels are deemed to belong to iron‐oxide grains. The well‐defined differences in density between the iron‐oxides and the other common minerals in basalt typically yield a bi‐modal or multi‐modal attenuation spectrum in the microCT analysis, and the minimum separating the high‐density peaks from the lower density matrix minerals can be selected as a threshold. It is important to set the threshold such that all iron‐oxide grains are included in the analysis, even if this implies that some non‐magnetic grains are also selected. After all, a grain that is selected can be assigned a (near) zero magnetization by the inversion, but missing an iron‐oxide grain in the microCT analysis leads to magnetic anomalies in the magnetic surface scan that cannot be properly assigned to their source. Setting the threshold for the attenuation contrast results in a list of voxels with their spatial coordinates that pass this selection. Groups of adjacent, interconnected, high‐density voxels form a precisely localized grain, for which also the size and shape are now approximately known. From these data, the volume, center of gravity, and distance to for example, the surface of the sample can be estimated for each grain individually.

The volume uncertainty related to voxel thresholding is difficult to assess because it critically depends on the grain's shape. The fact that a thin iron‐oxide plate with large volume but thickness below a fraction of the voxel width $ϵ$ would not be recognized shows that the error can be arbitrarily large. For bodies with surface area $A$ and volume $V$ the relative volume uncertainty is in the order of $Aϵ/V$, and thus for sphere‐like bodies with diameter $D$ decreases with $ϵ/D$. For the MMT technique, the most important information is the location and topological separation of the iron‐oxide grain or cluster which will be assigned a separate magnetic moment by the inversion. Only the interpretation of this magnetic moment in terms of a grain's magnetization requires the grain's volume with its much larger uncertainty due to voxel binarization (Heidig et al., 2017).

2.2. Scanning Magnetometry

Recent advances in scanning magnetometry techniques such as Scanning SQUID Magnetometry (SSM) (Egli & Heller, 2000; Lima & Weiss, ²⁰¹⁶; Weiss et al., ²⁰⁰⁷), instruments using a Magnetic Tunnel Junction (MTJ) (Lima et al., 2014), and the Quantum Diamond Microscope (QDM) (Farchi et al., 2017; Fu et al., ²⁰²⁰; Glenn et al., ²⁰¹⁷; Levine et al., ²⁰¹⁹) allow for quantitative measurements of the magnetic field on, or near, the surface of a sample in (sub)micrometer resolution. In theory, results from all these magnetic surface magnetometry techniques can be used for MMT. The proof‐of‐concept of MMT (de Groot et al., ²⁰¹⁸) was provided using an SSM, here we present MMT results based on MTJ and QDM measurements.

2.2.1. Scanning SQUID Set‐Ups

In scanning SQUID microscopy a Superconducting QUantum Interference Device (SQUID) sensor is used to measure magnetic fields above a sample. A SQUID sensor that consists of a superconducting loop containing Josephson junctions hovers over (or is in contact with) a sample and measures the component of the magnetic flux density perpendicular to its surface (Kirtley & Wikswo, 1999; Reith et al., ²⁰¹⁷). SQUID sensors in SSM set‐ups can attain effective magnetic moment sensitivities in the order of $10^{-16}{\mathrm{A}\mathrm{m}}^2$ and are therefore the most sensitive magnetometers to date. This makes them theoretically very suitable for MMT analyses. It is the requirement of superconductivity, however, that puts constraints on the usefulness of scanning SQUID set‐ups for MMT.

In the SSM set‐up used for the proof‐of‐concept of MMT (de Groot et al., ²⁰¹⁸) the sample was submerged with the SQUID sensor in liquid helium. This allows the SQUID sensor to be in contact with the sample and the sample‐sensor distance to be in the order of just 1–2 μm. This allows for a spatial resolution in the order of $\sim$1 μm, hence this SSM set‐up can exploit the full native sensitivity of SQUID sensors at unsurpassed spatial resolution. Nevertheless, the sample is measured at a temperature of $\sim$4 K—far below its Verwey transition. Therefore this set‐up impedes determining magnetizations of naturally occurring magnetic states in a sample at room temperature and is therefore only of limited use for paleomagnetic and rock‐magnetic applications of MMT.

In other SSM set‐ups previously used for paleomagnetic or rock‐magnetic applications the SQUID sensor is thermally isolated from the sample (e.g., Egli & Heller, ²⁰⁰⁰; Fong et al., ²⁰⁰⁵; Lima & Weiss, ²⁰¹⁶; Oda et al., ²⁰¹⁶; Weiss et al., ²⁰⁰⁷). This can only be attained by increasing the sample‐sensor distance, in the most recent set‐ups this distance can be as little as 200 μm (Oda et al., 2016); hence the spatial resolution limit of such set‐ups is in the order of 200 μm. In spite of the major technical achievement to thermally isolate the sample at room temperature from the SQUID sensor at $\sim$4 K over just 200 μm, the spatial resolution does not allow for a reliable magnetic inversion for individual grains in natural samples given the concentration of magnetic grains. Therefore also the thermally isolated SSM set‐ups seem unsuitable for MMT, even considering their unsurpassed magnetic sensitivity.

2.2.2. Magnetic Tunnel Junction Scanners

Advances in non‐cryogenic scanning magnetometry sensors have led to the development of Magnetic Tunnel Junction (MTJ) sensors that are suitable for paleomagnetic and rock‐magnetic applications (Lima et al., 2014). MTJ sensors exploit a quantum physical effect by which electrons can tunnel through an ultra‐thin insulating layer that is in between two ferromagnetic layers, creating a small current through the sensor. This tunneling effect is governed by the magnetization in the two ferromagnetic layers of the sensor. Therefore the tunneling current, and hence the resistance of the sensor, changes due to variations in the external magnetic field. The major advantage of these MTJ sensors over typical SQUID sensors is that MTJ sensors operate at room temperature, this makes the expensive and complex cryogenic systems for SSM set‐ups superfluous. Nevertheless, typical MTJ sensors are $>$4 orders of magnitude less sensitive compared to SQUID sensors (Lima et al., 2014). This major setback in sensitivity is only partially compensated by the smaller sample‐sensor distances that are possible in MTJ set‐ups (down to $\sim$7 μm). This results in typical effective magnetic moment sensitivities in the order of $10^{-14}{\mathrm{A}\mathrm{m}}^2$ for the most advanced MTJ set‐ups (Lima et al., 2014). The spatial resolution of an MTJ set‐up primarily depends on the actuators used to move the sensor or sample and is often in the order of $5-10$ μm.

The sensitivity of the surface magnetometry technique is not a major concern when making scans of synthetic or volcanic material. For the proof‐of‐concept of MMT (de Groot et al., ²⁰¹⁸), the sensitivity of the SSM set‐up had to be reduced in favor of dynamic range to properly image the magnetization of the sample. This makes MTJ‐based set‐ups theoretically very suitable for MMT analyses, primarily because of their small sample‐sensor distance and high spatial resolution. In this study, we obtained a magnetic surface scan of the same synthetic sample that was used in de Groot et al. (2018), on the MTJ set‐up at the University of Cambridge.

2.2.3. Quantum Diamond Microscope

Recently, an entirely new type of scanning magnetometry was optimized for geological samples: the Quantum Diamond Microscope (QDM) (Farchi et al., 2017; Fu et al., ²⁰²⁰; Glenn et al., ²⁰¹⁷; Levine et al., ²⁰¹⁹). The QDM uses optical fluorescence in nitrogen‐vacancy (NV) centers in a diamond chip to determine the magnetic field above a sample. The magnetic fields are thus derived from an optical image, hence its theoretical spatial resolution limit is determined by the diffraction limit of the optics. The wavelength of the fluorescence is 600–800 nm; the theoretical limit for the spatial resolution, therefore is $\sim$350 nm, depending on the quality of the optical path (Levine et al., 2019). In practice, however, current set‐ups attain a spatial resolution of 1.2 μm (Glenn et al., 2017). The sensitivity of the QDM depends on several variables, for example, the time over which the measurements are done, the thickness of the layer of NV centers in the diamond, and the characteristics of the optical components used. In general, the sensitivity of the QDM may be expected to be better than the sensitivity of MTJ sensors but does not attain the sensitivity of SQUID sensors (Glenn et al., 2017).

An important property and possible draw‐back of the QDM for MMT applications is that it needs a bias field to operate (Glenn et al., 2017). During normal operation, this bias field is approximately 0.9 mT and its polarity is switched many times. This enables discriminating between remanent (i.e., ferrimagnetic) and paramagnetic/viscous magnetizations. The QDM produces two maps: one of the remanent magnetizations that inherently misses the remanence carried by grains with a coercivity below the bias field; and another with the induced magnetizations by the bias field. Since the iron‐oxide grains that carry information on the past state of the Earth's magnetic field generally have coercivities higher than the bias field currently used (0.9 mT), this property of the QDM does not jeopardize the paleomagnetic interpretation of QDM results. But for some rock‐magnetic applications such as magnetic viscosity studies, however, this bias field needs to be considered.

Since the QDM is theoretically very suitable for MMT analyses, we obtained a magnetic surface scan of the same synthetic sample used for the MTJ analysis and for the proof‐of‐concept of MMT (de Groot et al., ²⁰¹⁸) at the QDM set‐up at Harvard University. Furthermore, we obtained a magnetic surface scan from a natural volcanic sample.

2.3. Co‐Registration

The two data‐sets for MMT, the spatial information on the iron‐oxide grains from the microCT analysis and the magnetic surface scan, must be co‐registered in the same coordinate system for a reliable inversion. This co‐registration consists of a mapping of the magnetic surface scan in the $x$ and $y$‐coordinates of the microCT data, and determining the sample‐sensor distance, or scan height, the $z$‐coordinate. For the SSM and MTJ data, the locations of the iron‐oxides closest to the surface as produced by the microCT scan are manually aligned with the largest magnetic anomalies present in the magnetic surface scan. Since the QDM is an optical acquisition technique, it is possible to make an optical image of the surface of the sample in exactly the same coordinates as the magnetic scan is made. This greatly eases the tedious, manual process of mapping the two data sets.

The sample‐sensor distance, or scan height, is often even more difficult to determine. But, since magnetic moments decay with the third power of distance, it is of utmost importance to have a good estimate of this parameter. The SSM sensor in the proof‐of‐concept was in contact with the sample, hence the sample‐sensor distance can be estimated with precision. For the MTJ and QDM set‐ups, this distance is derived from the actuators that are used to move the sensor (MTJ), or the sample (QDM), and maybe less precise, depending on the actuators used.

2.4. Inversion

The combination of microCT data and magnetic surface scans enables to uniquely reconstruct the magnetic moments of individual iron‐oxide grains in a sample, provided that they are spatially sufficiently separated. A grain is defined as a group of interconnected voxels in the microCT scan; each grain is considered to be uniformly magnetized. For the inversion each grain is mathematically isolated inside a small sphere ${\mathrm{\Omega }}^i$, $i=1\dots N$. These spheres cannot intersect, that is, they are pairwise disjoint. This implies that when grains are spatially not sufficiently separated, or when grains are intertwined, these grains can only be placed inside a sphere together and their magnetic moment is solved for as one. A number $N$ spheres ${\mathrm{\Omega }}^i$ are now considered to be magnetic source regions inside a larger sphere $\mathrm{\Omega }$. In a slightly simplified version, the underlying theorem for the inversion (Fabian & de Groot, 2019) guarantees that the radial magnetic field component $B_r^{\mathrm{\Omega }}$ on the sphere $\mathrm{\Omega }$ uniquely defines the radial field components $B_r^i$, $i=1\dots N$, on the surfaces of all of the $N$ inner spheres ${\mathrm{\Omega }}^i$ (Fabian & de Groot, 2019). To apply this theorem in practice, all magnetic sources in a sample have to be identified and placed into $N$ pairwise separate spheres, such that each magnetic grain lies completely inside one of these spheres, and no magnetic sources are outside them. It is then theoretically possible to identify the magnetic dipole moment of each of the $N$ spheres from a precise measurement of $B_r^{\mathrm{\Omega }}$ on a spherical surface around all $N$ spheres.

In practice, the magnetic scanning measurement is performed at finitely many positions on a sufficiently large rectangular planar region $R\subset \mathrm{\Omega }$ above the sample. This rectangle mathematically corresponds to a fraction of an infinitely large sphere, which is chosen large enough, such that the field component $B_r^{\mathrm{\Omega }}$ outside $R$ is negligibly small. Conceptually, the inversion proceeds through the following steps:

• 1.Define the scan surface $R$ and the centers and sizes of the $N$ spheres $c_i$, $i=1\dots N$ that contain all sources. These spheres are determined by assuming that all magnetic sources are identified by density anomalies in the microCT data
• 2.Measure $B_r^{\mathrm{\Omega }}$ on $R$ with sufficient resolution and accuracy
• 3.Use the unique continuous (Fabian & de Groot, 2019) inversion operator

$$B_r^{\mathrm{\Omega }}\to B_r^i$$

to calculate the radial component on the surface ${\mathrm{\Omega }}^i$ of the $i$‐th sphere.

• 4.Decompose $B_r^i$ in spherical harmonics to isolate its dipole moment $m_i$

This conceptual procedure shows that in case of sufficient accuracy and resolution the dipole moments $m_i$ are uniquely defined, and can be recovered with arbitrary precision. Because the recovery essentially involves a downward continuation of the radial field from the larger sphere $B_r^{\mathrm{\Omega }}$ to each smaller sphere $B_r^i$, it substantially amplifies noise and requires extremely precise and accurate data to succeed (e.g., Blakely, ¹⁹⁹⁵).

2.4.1. Inversion Routine

The practical inversion routine used here is described in de Groot et al. (2018). It exploits the more detailed geometric information from the microCT to obtain a representation of the shapes of individual grains as a union of a small number of rectangular boxes (i.e., cuboids). Each grain $P_i$, $i=1,\dots ,N$, is described as a union of $n_j$ cuboids $C_{i,j}$ with $j=1,\dots ,n_j$, each of which is homogeneously magnetized with magnetization $M_i$. For each scanning point $r_k$, $k=1\dots K$ the forward model equation calculates the magnetic flux through the sensor on the surface of the sample generated by each cuboid $C_{i,j}$ as function of its magnetization vector ${\mathbf{M}}_{\mathbf{i}}=(M_{i,1},M_{i,2},M_{i,3})$. The sum provides the total flux $F_k$ as a linear function of the $3N$ parameters defining all vectors ${\mathbf{M}}_{\mathbf{i}}$. Thereby the forward model defines a $K\times 3N$ design matrix $\mathbf{A}$ which transforms the vector

$$\mathbf{v}=(M_{1,1},M_{1,2},M_{1,3},M_{2,1},M_{2,2},M_{2,3},\dots ,M_{N,2},M_{N,3})$$

into the measured flux signals

$$\mathbf{F}=(F_1,F_2,F_3,\dots ,F_K),$$

according to the forward equation

$$\mathbf{F}=\mathbf{A}\mathbf{v}.$$

The inversion is performed by calculating the Moore‐Penrose pseudoinverse ${\mathbf{A}}^{+}$ (Moore, 1920; Penrose, ¹⁹⁵⁵) and applying this to the vector ${\mathbf{F}}_{\text{MMT}}$ of the measured values of $F_k$ via

$${\mathbf{v}}_0={\mathbf{A}}^{+}{\mathbf{F}}_{\text{MMT}}.$$

By definition of the pseudoinverse, for $K>3N$ this returns the vector ${\mathbf{v}}_0$ of all magnetizations for the least‐square fit of the measured values by assuming a homogeneous magnetization for each grain.

Due to the geometrical approach of this routine, it produces magnetizations (i.e., volume normalized magnetic moments, of the grains. In contrast to magnetic moments, these magnetizations are prone to uncertainties arising from the microCT data processing, such as resolution limits, thresholding, and voxel binarizations. Multiplying the magnetizations by the same volumes that were used in the inversion procedure yields the magnetic moments of the grains that explain the observed magnetic anomalies in the magnetic surface scan best. These magnetic moments are insensitive to the uncertainties in the volume estimates associated with the microCT data processing.

2.5. Residuals

The accuracy of the inversion can be assessed by calculating the residuals left by the inversion. This is done by assigning all grains their calculated magnetic moment and running a forward model to determine the resulting magnetic map on the surface of the sample. This calculated magnetic surface map is then subtracted from the actual, measured, magnetic surface scan. This produces a map of the residuals after the inversion, that is, a map of the measured magnetic flux on the surface that is not explained by the calculated magnetic moments of the grains. After an accurate inversion, we expect low residuals; high magnetic anomalies in the residuals often arise from larger grains close to the surface. Their magnetic expressions on the surface of the sample are generally more complex due to their complex magnetic domain states. Therefore these magnetic anomalies cannot be explained by our assumption of dipolar magnetic moments in the grains.

3. Obtaining Magnetic Directions From MMT

To obtain a magnetic direction from magnetizations of individual grains as produced by our inversion routine (Section 2.4.1), we first determine the magnetic moments ($\mathbf{m}$, in ${\mathrm{A}\mathrm{m}}^2$) of the individual grains by multiplying their calculated magnetizations ($\mathbf{M}$, in A/m) by their volume. We also change the mathematical indices $1,2,3$ describing the axes of the coordinate system used in Section 2.4 to the axes they physically represent: $x,y,z$; with the x‐y‐plane as the surface of the sample and z going down into the sample from its surface. The total magnetic moment of the grain is then given by:

$$m_{\text{grain}}=\sqrt{m_x^2+m_y^2+m_z^2}$$

The magnetic direction is defined by a declination and inclination with respect to the coordinate system of the sample. The declination is defined as the angle with the positive x‐axis of the sample in the x‐y‐plane; the inclination is defined as the smallest angle with the positive z‐axis of the sample:

$$\text{dec}=\arctan (m_x/m_y)\mathrm{a}\mathrm{n}\mathrm{d}\text{inc}=\arcsin (m_z/m_{\text{grain}})$$

To calculate the bulk magnetization for the entire sample based on all grains or a sub‐set of grains, first the $m_x$, $m_y$, and $m_z$ components of the selected grains are summed into $\mathrm{\Sigma }{m}_x$, $\mathrm{\Sigma }{m}_y$, and $\mathrm{\Sigma }{m}_z$. Then these parameters are used in the equations above.

3.1. A Magnetic Direction from an MTJ Scan

To obtain a magnetic direction using MMT we used the same synthetic sample as used in de Groot et al. (2018). This sample contains 128 magnetite grains with diameters ranging from 5 to 35 μm that are randomly distributed in space (Movie S1). First, we gave it an isothermal remanent magnetization (IRM) with a pulsed magnetic field of 1 T perpendicular to the surface of the sample, to give the sample a known magnetic state. This was done by suspending the sample in a Lakeshore Vibrating Sample Magnetometer at the University of Cambridge and briefly switching on the field. The sample was scanned in the MTJ set‐up at the University of Cambridge directly after giving the sample its IRM. The entire surface of the sample was scanned with a step size of 10 μm, yielding 8,736 data points, with a scan height of 33.56 μm (Table 1). The scan shows some scanning artifacts in the scan direction, identified as diagonal stripes (Figure 2a). The MTJ scan shows large positive magnetic anomalies, up to $>$30 μT, and much smaller negative anomalies, down to <$-5$ μT. This differs from the observations in de Groot et al. (2018), where the positive and negative magnetic anomalies seem more symmetrical distributed around 0 μT. This can be explained by the much larger scan height used in the MTJ scan: 33.56 versus 2 μm for the SSM set‐up used in de Groot et al. (2018). Since the scanner is further away from the magnetic sources, the magnetic expression of the sources represents more their “far‐field” (i.e., dipolar) nature. Moreover, the MTJ scan was made after giving the sample an IRM, while the magnetic states in de Groot et al. (2018) represent a more natural magnetic state. Hence the grains were much stronger and more uniformly magnetized during the MTJ scan.

Table 1.

Details of the Micromagnetic Tomography Inversions

	Synthetic sample		Volcanic sample
			Area 1	Area 2	Area 3	Area 4
Magnetic scan
Scanning technique	MTJ	QDM	QDM	QDM	QDM	QDM
Sensor geometry	${\mathrm{e}\mathrm{l}\mathrm{l}\mathrm{i}\mathrm{p}\mathrm{s}\mathrm{e}}^a$	square	square	square	square	square
Sensor surface (μ${\mathrm{m}}^2$)	8.0	1.44	1.44	1.44	1.44	1.44
Datapoints (x, y)	91 $\times$ 96	170 × 166b	126 $\times$ 126	209 $\times$ 230	167 $\times$ 138	184 $\times$ 130
Scan height (μm)	33.56	6.0	6.0	6.0	6.0	6.0
Step size (μm)	10.0	6.${\mathrm{0}}^b$	1.2	1.2	1.2	1.2
Spatial information
MicroCT resolution (μm)	0.714	0.714	0.675	0.675	0.675	0.675
MicroCT voxel size (μ${\mathrm{m}}^3$)	0.36	0.36	0.31	0.31	0.31	0.31
Scan dimensions (x, y, z; μm)	910 × 960 × 50	1020 × 996 × 50	150 × 150 × 30	250 × 275 × 30	200 × 165 × 30	220 × 155 × 30
Number of grains	128	128	11	42	18	20
Number of cuboids	19,552	19,552	305	1,192	388	555
Grain concentration (grains/${\mathrm{m}\mathrm{m}}^3$)	2,930	2,520	16,300	20,360	18,180	19,550

^a modeled as a square of 2.83 $\times$ 2.83 µm.

^b after subsampling the original quantum diamond microscope scan which has a step size of 1.2 µm.

Figure 2.

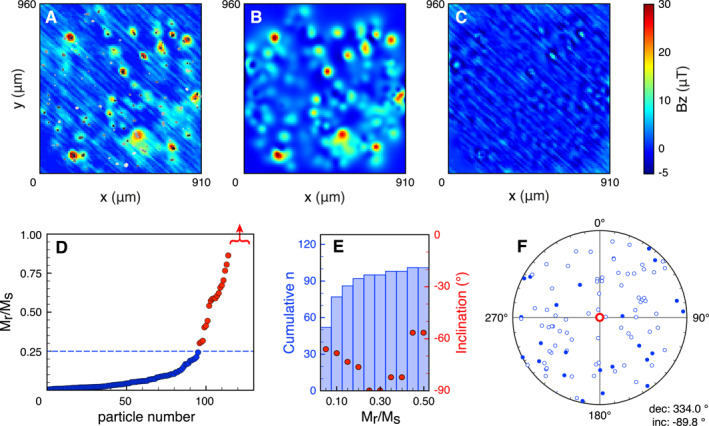
Results of Magnetic Tunnel Junction (MTJ) experiments on the synthetic sample. The 128 grains in the sample are superimposed on the MTJ measurements (in gray‐scale, a). The outcome of the forward calculations is in b, the map of the residuals is in (c) The theoretical remanence ratios (Mr/Ms) of the individual magnetite grains (see main text) are sorted in increasing order (d). The graph is clipped at the theoretical maximum Mr/Ms ratio of 1; 14 grains with Mr/Ms ratios between 1.08 and 9.45 are not shown, indicated by the red arrow. For cumulative bins of Mr/Ms ratios, the cumulative n is plotted together with the resulting inclination for the selected grains (e). For grains with Mr/Ms ratios $<$0.25 (blue dashed line in d), the resulting direction differs just 0.$\mathrm{2}°$ from the expected direction. For these grains, the distribution of their individual directions is in f (open symbols pointing upwards, closed symbols downwards), with the resulting direction in red.

The co‐registration between the MTJ and microCT results was done manually by aligning the locations of the grains closest to the surface to the strongest magnetic anomalies in the MTJ scan (Figure 2a). The co‐registration was accurate and allowed for a proper inversion; magnetizations were obtained for all 128 grains in the synthetic sample (Table S1). The results of the inversion were used as input for a forward model (Figure 2b) which yields a close representation of the magnetic surface scan (Figure 2a). This leads to generally very low residuals (Figure 2c). The diagonal scanning artifacts in the MTJ scan are the most prominent feature in the residuals, hence the inversion is insensitive to these, and they are not propagated into the calculated magnetizations per grain.

From this dataset alone it is difficult to label magnetizations of individual grains “reliable” or “unreliable.” In the future, this could be done by e.g., determining the magnetizations of individual grains after series of magnetic treatments. Nevertheless, it is possible to provide a first‐order assessment of the accuracy of the magnetizations produced here by considering the theoretical remanence ratios (Mr/Ms) of the individual grains. These can be estimated by dividing the remanent magnetization (Mr) of the individual grains as produced by the inversion, by their theoretical saturated magnetization (Ms) (Figure 2d). Since the grains in the synthetic sample are pure magnetite grains, their theoretical saturation magnetization is $480{\mathrm{k}\mathrm{A}\mathrm{m}}^{-1}$ (Dunlop & Özdemir, 1997). It is important to note that we use the volume estimates of the grains as produced by the microCT analysis to determine both the Mr and Ms values. The uncertainties associated with the manual thresholding and voxel binarizations during microCT data interpretation, therefore, propagate into the calculated magnetizations. Nevertheless, the volumes for all grains were obtained in a single workflow using one threshold. Since our analysis based on the Mr/Ms ratios is comparative in nature the absolute uncertainties in volume estimates are somewhat suppressed in our analysis. Moreover, the resulting magnetic directions for subsets of grains in the sample are based on the individual magnetic moments of grains that are insensitive to the uncertainties in the volume estimates.

Most grains have low Mr/Ms ratios, as expected since the grains in the synthetic sample have diameters ranging from $5-35$ μm. Some grains, however, have Mr/Ms ratios that are much larger than expected; they are well above 0.5, and some Mr/Ms ratios are even higher than the theoretical limit of 1. For these grains, it is most likely that the inversion did not produce accurate estimates of the magnetization, and they should be excluded from calculating the magnetic direction for the entire sample. Besides this theoretical maximum, there is no theoretical value for the cut‐off for the Mr/Ms ratios to select the grains that should be included in calculating the magnetic direction. Therefore we took an iterative approach to select the grains based on their Mr/Ms ratios that yield a resulting magnetic direction closest to the applied magnetic field. Furthermore, the resulting direction should be insensitive to the addition of small numbers of grains to the ensemble – adding one or two grains should not have a major effect on the resulting direction. Since we know that the expected paleodirection is perpendicular to the surface we expect an inclination of $-90°$, with any value for the declination. We calculated the magnetic direction for grains based on their Mr/Ms ratio, starting with grains with Mr/Ms ratios $\le 0.05$. We then added grains based on their Mr/Ms ratio in bins of 0.05, until the Mr/Ms ratio reached 0.5. This results in pairs of number of grains included (n) and the resulting inclination (Figure 2e). For the grains with Mr/Ms ratios $\le$ 0.25, the resulting inclination is $-89.8°$, with a declination of $334.0°$. This is just $0.2°$ off of the expected direction (Figure 2f). For the next bin, with Mr/Ms ratios $\le 0.35$ (the bin between 0.25 and 0.30 has no additional grains), three additional grains are included in calculating the magnetic direction. These three grains have a large influence on the resulting inclination, making the resulting direction very sensitive to individual grains and therefore unstable (Figure 2e). Moreover, Mr/Ms ratios up to 0.25 are plausible for grains with diameters ranging from $5-35$ μm (e.g., de Groot, Dekkers, et al., ²⁰¹⁴; Monster et al., ²⁰¹⁸).

3.2. A Magnetic Direction From a QDM Scan

To test the performance of MMT using different magnetic surface scanning techniques we repeated the experiment with the MTJ using the QDM at Harvard University (Table 1). We used the same synthetic sample again and gave it a 1 T IRM field perpendicular to its surface using an ASC Impulse Magnetizer (IM‐10‐30) at the Massachusetts Institute of Technology. The magnetic surface scans were made the same day. Since the QDM also produces an optical image of the sample in the same coordinate system as the magnetic scan, the mapping between the QDM scan and the spatial data from the microCT scan was relatively easy (Figure 3a). The sample‐sensor distance in the QDM is much smaller compared to the MTJ scan, the magnetic anomalies are therefore larger ($\sim$100 μT for the QDM, compared to $\sim$30 μT for the MTJ). The inversion yielded magnetizations for all 128 grains in the sample (Table S2). These magnetizations were used to make a forward calculation of the surface magnetization (Figure 3b), and a map of the residuals left by the inversion (Figure 3c). The residuals are low, although there are prominent and complex anomalies over some grains, usually grains closer to the surface. These observations are explained by the smaller sample‐sensor distance of the QDM compared to the MTJ: complex, non‐dipolar, structures are only observed in close proximity of the grains. To interpret the resulting magnetic direction for the entire sample we followed the same workflow as for the MTJ scan. First, the Mr/Ms ratios were calculated for the individual grains using their theoretical Ms of $480{\mathrm{k}\mathrm{A}\mathrm{m}}^{-1}$. More than 100 grains have an Mr/Ms ratio $<$0.10. Since we used the same grain volumes for the MTJ and QDM data analyses, this implies that the magnetizations of the grains (and hence their Mr/Ms ratios) from the QDM scan are generally somewhat lower than those from the MTJ scan (Figure 3d). Again, we use bins of 0.05 for the Mr/Ms ratios and calculate the resulting inclination (Figure 3e). For the set of grains with Mr/Ms ratios between 0 and 0.10 the inclination is $-77.1°$, this is closest to the expected inclination of $-$90° for any of the Mr/Ms ratio bins up to 0.5, but still $-12.9°$ off. The declination for this resulting direction is $\text{261.7}°$. Furthermore, the number of grains with a direction in the upper hemisphere (i.e., with a direction more than $\mathrm{90}°$ off of the applied magnetic field) is 24 for the MTJ experiment and only four for the QDM experiment (compare Figures 2f and 3f). This implies that the distribution of the directions of the individual grains seems narrower for the results using the MTJ scanner compared to the QDM results.

Figure 3.

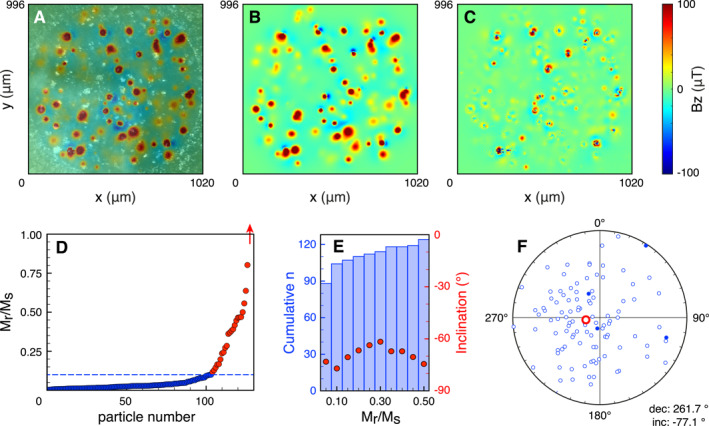
Results of Quantum Diamond Microscope experiments on the synthetic sample. The optical microscopy image is in the background in gray‐scale (a), the map of the magnetic flux density perpendicular to the surface (in color) is super‐positioned with 50% transparency. The outcome of the forward calculations is in b, the map of the residuals is in (c) The theoretical Mr/Ms ratios of the individual magnetite grains (see main text) are sorted in increasing order (d). The graph is clipped at the theoretical maximum Mr/Ms ratio of 1; one grain with a Mr/Ms ratio of 2.42 is not shown, as indicated by the red arrow. For cumulative bins of Mr/Ms ratios, the cumulative n is plotted together with the resulting inclination for the selected grains (e). For grains with Mr/Ms ratios $<$0.10 (blue dashed line in d), the resulting direction is closest to the expected direction. For these grains, the distribution of their individual directions is in f (open symbols pointing upwards, closed symbols downwards), with the resulting direction in red.

It is currently difficult to explain the differences between the MTJ and QDM studies using the same sample and magnetic treatment in more detail. These differences may have experimental reasons, e.g., the smaller sample‐sensor distance in the QDM leads to detecting more complex magnetic signals, and our assumption to solve for dipolar magnetizations may be violated. Furthermore, the IRM imparting field was applied directly preceding the MTJ scan at the University of Cambridge; while for the QDM experiment the sample had to be transported from the Massachusetts Institute of Technology to Harvard. Although the sample was measured on the QDM within hours after applying the IRM, the additional time and handling of the sample before the QDM scan might have given potential viscous processes more time to evolve. There can also be a rock‐magnetic reason for the observed differences: the coercivities of some grains may be (partially) very low, so their signal would be (partially) canceled by the switching bias field applied in the QDM (0.9 mT), leading to lower total magnetizations in the QDM experiment. Nevertheless, it is encouraging to see that the resulting magnetic directions from both the MTJ and QDM experiments are close to the expected direction and that it is possible to select and consider the contributions of individual grains in a sample.

4. Rock‐Magnetic Information From a Volcanic Sample

The concentration of magnetic grains in the synthetic sample is about one order of magnitude lower than the concentration of magnetic grains in naturally occurring lavas (Table 1). To test whether MMT is also capable of determining magnetizations of individual grains in a natural sample we subjected a sample from an Hawaiian lava flow to an MMT study. We drilled a small core with a diameter of 3 mm from a standard thin section with a sample thickness of 30 μm from the 1907 flow of the Kilauea (site HW03 from de Groot et al. [2018]). Our sample was taken from the same paleomagnetic drill core as the sample used in ter Maat et al. (2018) where the chemical, physical, and magnetic states of several individual iron‐oxide grains were thoroughly assessed with for example, scanning electron microscopy, electron back‐scatter diffraction, magnetic force microscopy, and micro‐probe analyses. The sample was polished using a colloid silica suspension prior to the magnetic scans to remove surface magnetizations due to mechanical polishing (see Figure S9 in de Groot, Fabian, et al. [2014]). The magnetic surface scan was made with the QDM at Harvard University. We did not apply any magnetic treatment to the sample beforehand; the magnetizations of the grains therefore most likely resemble a natural magnetic state. The iron‐oxide grains in the sample were obtained from a microCT scan done at the Nanotom‐S at TU Delft. The spatial resolution in this scan is $\sim$0.7 μm.

We used the optical image of the QDM to map the magnetic surface scan on the spatial data of the iron‐oxide grains obtained by the microCT scan. To reduce computation time the inversions were done for four small areas of the sample (Figure 4a). We obtained magnetizations for all 91 grains inside the four areas. The residuals left by the inversion are low compared to the residuals reported for the synthetic sample (Figure 4c) and are again dominated by complex magnetizations arising from grains close to the surface of the sample.

Figure 4.

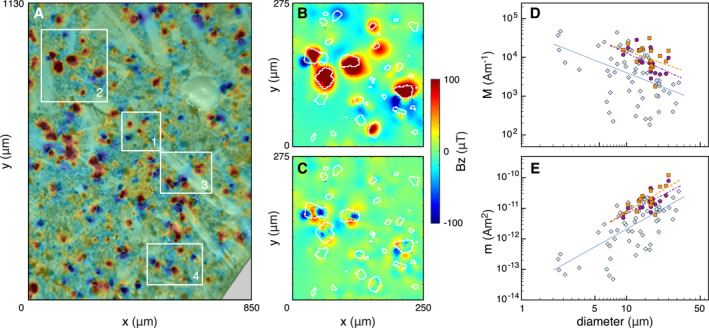
Results of Quantum Diamond Microscope (QDM) experiments on a volcanic sample (HW03, see main text). The optical microscopy image is in the background in gray‐scale (a), the map of the magnetic flux density perpendicular to the surface (in color) is super‐positioned with 50% transparency. The QDM data of area 2 (a) is in b, with the outlines of the iron‐oxide grains as identified by microCT in white. The residual after the inversion to produce the individual magnetic moments per grain (c) are generally low and non‐uniform, indicating a proper inversion result. The magnetizations (d) and magnetic moments (e) of grains with Mr/Ms ratios $\le$ 0.10 (see main text) are plotted as function of their diameter as blue diamonds, with their linear trend line in blue. The results of de Groot et al. (2018) are also included for comparison: the magnetizations arising from a “natural magnetic state” in purple circles/dashed trend line, and the magnetizations after applying an anhysteretic remanent magnetization with a bias field of 40 μT in orange squares/dashed trend line.

To assess the reliability of the inversion results we again calculated the theoretical Mr/Ms ratio for each grain, using the Ms of pure magnetite. The naturally occurring grains in Hawaiian lavas are generally rich in Ti; Curie balance experiments on sister samples from site HW03 exhibit a gradual decay of the magnetization with temperature, with Curie temperatures around 250 and $\mathrm{450}°$C that are not very well expressed (de Groot et al., ²⁰¹³; ter Maat et al., ²⁰¹⁸). Replacing Fe by Ti in the iron‐oxide solid solutions lowers the Ms values (Dunlop & Özdemir, 1997; Readman & O'Reilly, ¹⁹⁷²). It is therefore safe to assume that the Ms of pure magnetite is overestimating the real Ms value for most of the grains in the sample, leading to artificially low Mr/Ms ratios for our volcanic sample.

From the 91 grains in the inversions, 16 grains have Mr/Ms ratios higher than the theoretical maximum of 1. These grains were thus not properly resolved by the inversion and were rejected. Building on the experience with the QDM results for the synthetic sample and given that the Ms value for magnetite is overestimating the true Ms values for our grains, we deem the grains with Mr/Ms ratios $>$0.10 suspect. These grains are not considered further in our analyses. This leaves 62 grains for which the magnetizations are now known. These magnetizations are plotted against the diameters of the grains that are obtained from the microCT analysis (Figure 4d). Since the volume of the grains is known, their magnetic moments can be calculated and plotted as a function of their diameter as well (Figure 4e).

The natural sample was not magnetically treated prior to the QDM measurements, the magnetizations are therefore most likely resembling a natural magnetic state. In a study by de Groot et al. (2018), the pure magnetite grains in the synthetic sample were also either untreated prior to the SSM measurements (in purple in Figures 4d and 4e) or analyzed after applying an anhysteretic remanent magnetization (ARM) with a bias field of 40 μT to the sample (in orange in Figures 4d and 4e). The magnetic states in de Groot et al. (2018) therefore also resemble a natural magnetic state and can be meaningfully compared to the magnetic states of our natural sample. The magnetizations of the grains in the natural sample are on average lower than the magnetizations for the synthetic sample. This is explained by the grains being enriched in Ti in the natural sample, lowering their magnetizations. The trends in magnetization and magnetic moment as a function of diameter, however, are remarkably similar for the natural sample compared to the trends resolved for the pure magnetite grains in de Groot et al. (2018).

5. Discussion

Building on the proof‐of‐concept of MMT (de Groot et al., ²⁰¹⁸), we showed that it is possible to obtain a magnetic direction from a subset of grains in a synthetic sample, and derive magnetic information from individual grains in a natural volcanic sample. Here we will first discuss the technical characteristics and limitations of MMT, and then its potential for both paleomagnetism and rock‐magnetism.

5.1. Spatial Characterization of the Grains

5.1.1. Detecting all Iron‐Oxides

The spatial characteristics of all iron‐oxide grains in the sample are determined from a microCT scan. For a reliable inversion, all magnetic sources must be properly identified, otherwise, not all magnetic surface anomalies can be attributed to their source. Being able to detect all potentially magnetic iron‐oxides depends on selecting the proper threshold in the microCT scan above which grains are deemed iron‐oxides, and the resolution of the microCT scan. Since the iron‐oxides have a distinct density contrast to most other minerals present in volcanic samples, and also to artificial matrices such as epoxy, the attenuation spectrum from the microCT scan is often bi‐ or multi‐modal. Selecting the low between two modes is often straightforward, but the threshold should be chosen conservatively such that all iron‐oxides in the sample are selected. As de Groot et al. (2018) already noted, selecting the proper attenuation threshold paradoxically was easier for the volcanic sample with less distinct density differences between the grains, than for our synthetic sample with large differences in density between the matrix and the magnetite grains. The smaller differences in density most probably suppress adverse beam hardening effects and therefore boundaries between grains are better defined in the scans.

The resolution of the microCT used here and in de Groot et al. (2018), the Nanotom‐S at TU Delft, is $\sim$0.7 μm, so it inherently misses grains that are below $\sim$1 μm (Figure 5a). The grains in the synthetic sample that we used were sieved to be larger than 3 μm, but in natural samples, many grains with sizes between the superparamagnetic threshold of 30–50 nm (Dunlop & Özdemir, 1997) and the resolution limit of the Nanotom‐S may be present. Such smaller grains, however, have not been observed on a large scale in the scanning electron microscopy, microprobe, and magnetic force microscopy experiments on sister specimens of our HW03 sample (ter Maat et al., ²⁰¹⁸), while these techniques do have the necessary resolution to detect much smaller grains than the microCT used in this study. Furthermore, it is important to keep in mind that relatively small grains that may be missed by the microCT analysis have relatively little contribution to the total magnetic signal of volcanic samples. Although the TRM of a grain with a diameter of 100 nm is 28 times higher than the TRM of a grain with a diameter of 5 μm (Figure 5a); when the volumes of these grains are taken into account and their magnetic moments (m) are considered, the magnetic moment of the 5 μm grain becomes $4.5\times 10^3$ times larger than the magnetic moment of the 100 nm grain. This implies that $4.5\times 10^3$ grains of 100 nm have to be uniformly magnetized to produce the same magnetic moment as one grain with a diameter of 5 μm. In a natural sample where grains are not uniformly magnetized, however, it is more likely that ${\mathrm{10}}^5$ to ${\mathrm{10}}^6$ 100 nm grains are necessary to produce the same net moment as one 5 μm grain. This illustrates that the larger grains can very well be dominant in the overall magnetic signal of a sample.

Figure 5.

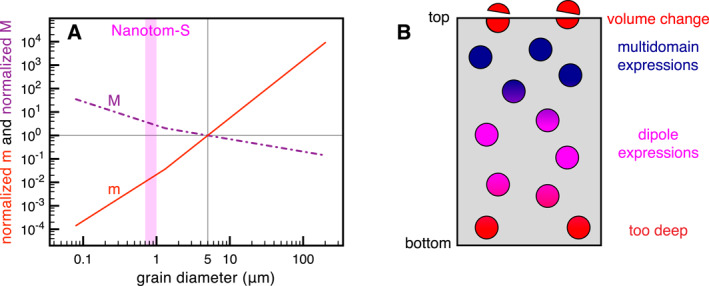
The spatial characterization of magnetic sources in a sample. The magnetization (M, in purple) and magnetic moment (m, in red) of spherical grains arising from a thermoremanent magnetic state vary as a function of their diameter (a). The data are normalized to the values for a 5 μm grain. The detection limit of the Nanotom‐S microCT is pink. Figure adapted from Figure 7.10 in Tauxe (2010), based on data presented in Dunlop and Özdemir (1997). How well MMT can determine the magnetization of the grains (represented by the circles) depends on their depths in the sample (b). The grains at the surface are cut during sample preparation and therefore lose their natural magnetization (top grains, in red); the magnetic expression of shallow grains may represent a complex “multidomain” magnetic configuration (in blue); the magnetic expression of somewhat deeper grains represent their far‐field, dipolar, magnetic moment (in pink); and the magnetic anomalies arising from grains that are too deep in the sample (in red) may be too weak to be properly inverted into the magnetization of the grains.

Current advancements in microCT scanners allow for resolutions down to $\sim$100 nm, this is very close to the superparamagnetic threshold of 30–50 nm for magnetite grains (Dunlop & Özdemir, 1997). This implies that it is already technically possible to detect iron‐oxides down to volumes where their contributions to the total magnetization of the sample become de facto negligible compared to the contributions of larger grains. Hence it is already possible to detect all (relevant) iron‐oxides in natural samples, although the field of view of scans with such high resolution is often relatively narrow and many scans should be combined to characterize the necessary amount of iron‐oxide grains for paleomagnetic interpretations.

5.1.2. Variation in Iron‐Oxides

Not all iron‐oxide grains do have remanent magnetizations at room temperature. The Ti‐rich end‐members of the titanomagnetite and titanohematite solid solutions (ülvospinel and ilmenite, respectively), for example, have Curie temperatures <$-100°$C (Readman & O'Reilly, 1972). To make it even more complex, scanning electron microscope (SEM) studies show that large iron‐oxide grains in natural lavas often exhibit several regions of different composition or show exsolution lamellae (e.g., Greve et al., ²⁰¹⁷; de Groot, Dekkers, et al., ²⁰¹⁴; Monster et al., ²⁰¹⁸). This is certainly the case for our volcanic sample, HW03 (de Groot et al., ²⁰¹³), as illustrated with a sister specimen taken from the same paleomagnetic drill core that was used to prepare the sample in this study by ter Maat et al. (2018). In this study, it was confirmed that zones that are identified as ilmenite using scanning electron microscopy, electron back‐scatter diffraction, and microprobe analyses are indeed non‐magnetic at room temperature by magnetic force microscopy. Currently, it is impossible to spatially discriminate between magnetic and non‐magnetic zones inside grains with the microCT techniques we used. Therefore many of the grains in our natural sample will have non‐magnetic zones; their “magnetic grain size” is therefore often smaller than the physical grain size detected by microCT analysis. This implies that the volumes used to estimate the magnetizations of individual grains are often larger than the regions that actually carry a magnetization in the iron‐oxide grains, leading to estimates of the magnetizations that are too low. This effect, however, does not impact the magnetic moments of the grains, since they are insensitive to their volumes.

The grains in both our synthetic and volcanic samples are mostly spherical in shape. From SEM studies it is known that in many lava samples that produce accurate paleointensities dendritic iron‐oxide grains are the dominant magnetic carrier (e.g., Cromwell et al., ²⁰¹⁵; ter Maat et al., ²⁰¹⁸). It is postulated that individual branches of dendritic grains act as small, individual, magnetic grains, with a favorable magnetic behavior compared to larger spherical grains. Because of resolution limits and noise effects such as beam hardening these dendritic grains are more difficult to characterize by microCT analyses. Moreover, it is currently unclear how the magnetic behavior of dendritic grains should be modeled in an MMT inversion. Dendritic grains therefore currently pose a challenge to be properly resolved in MMT studies.

5.1.3. Spatial Limitations as Function of Depth

The MMT technique determines magnetizations of all grains in the sample from a magnetic surface scan of such a sample. The expression of a grain's magnetization on the sample's surface decays as a function of depth in the sample to the power of three. This implies that the depth of a grain dictates how well MMT can resolve its magnetization (Figure 5b). Grains on the surface of a sample are cut during sample processing and polishing. Therefore their volume changes and their natural magnetization is lost. For grains close to the surface but not physically altered during sample processing we often observe complex magnetic anomalies on the surface of the sample (e.g., Figure 3c). We explain these as expressions of multidomain configurations in the grains. These complex anomalies in the magnetic surface scan violate our assumption to assign a dipolar magnetization to each individual grain, hence they are often left in the residuals after the inversion. It is debatable how well the dipole estimate actually represents the magnetization of grains in this zone of multidomain expressions (Figure 5b). For deeper grains, the magnetic expression on the surface represents more a far‐field magnetization – i.e., a dipolar magnetic configuration. For this zone of dipole expressions MMT is able to reliably determine the dipole moment of individual grains. For even deeper grains the magnetic expression on the surface of the sample becomes so weak that it becomes impossible to reliably invert for their magnetizations.

The specific depths of the different zones depend mostly on the sample‐sensor distance and the noise level/sensitivity of the magnetic scan used. This is best illustrated by comparing our MTJ experiment (with a scan height of 33.56 μm) to the QDM study (with a scan height of 6 μm) on the same synthetic sample. In the MTJ experiment, there are hardly complex magnetic anomalies left in the residuals (Figure 2c), while they are evident in the residuals of the QDM scan (Figure 3c). The larger scan height of the MTJ leads to detecting more of a far‐field magnetic expression of the magnetization of the shallower grains, and therefore a better approximation of their dipole fields. The zone of multidomain expressions (Figure 5b) is thus much smaller (if not absent) in the MTJ experiment. The inversion of the MTJ experiment, however, assigns more unrealistically large magnetizations to mostly deeper grains in the sample (compare Figures 2d and 3d). These are explained by the large scan height of the MTJ: the total source‐sensor distance can be $>$80 μm. This implies that the anomalies arising from deeper grains as measured by the MTJ sensor are very weak. This makes it difficult for the inversion to reliably determine their dipole magnetization; a weak magnetic anomaly often “disappears” in the noise level of the magnetic scan ‐ generally leading to overestimates of the dipole magnetizations of these deeper grains. The zone of dipolar expressions allowing for successful dipole inversions in the MTJ data is thus closer to the surface than for the QDM scan.

5.2. Scanning Magnetometry

We demonstrated that the MMT technique can be used with different magnetic surface scanning techniques. The potential of each of these techniques for MMT is governed by their spatial resolution and sensitivity (Figure 6a). The necessary spatial resolution of the magnetic scan is dictated by the concentration of magnetic grains in the sample and the sample thickness (Figure 6b). Considering that grains are randomly distributed in a sample and grains can be in very close proximity to each other, and may also be located above and below each other, not all grains are very well separable in a magnetic surface scan. A higher concentration of grains in a sample obviously leads to more magnetically obscured grains. The MMT inversion performs best if the system is vastly over‐determined – i.e., when there are many data points in the magnetic surface scan per variable to solve. To provide a dipole magnetization for a grain, the three orthogonal axes of its magnetization have to be solved for; the amount of variables in the system is therefore three times the amount of grains present in the sample.

Figure 6.

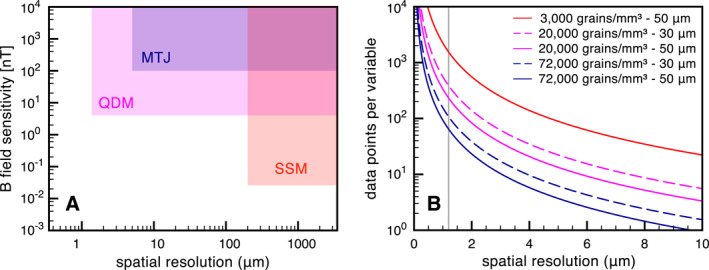
The resolution of the magnetic surface scan. Three potential scanning magnetometry techniques for Micromagnetic Momography (MMT) have different specifications for spatial resolution and B field sensitivity (a) (with data obtained from Fu et al., ²⁰²⁰; Glenn et al., ²⁰¹⁷; Lima et al., ²⁰¹⁴; Oda et al., ²⁰¹⁶). The theoretically available number of data points per variable that is to be solved by the MMT inversion is governed by the concentration of grains in the sample, the thickness of the sample, and the spatial resolution (i.e., step size) of the magnetic scan (b). The theoretically available number of data points per variable are given for the synthetic sample (3,000 grains/${\mathrm{m}\mathrm{m}}^3$ ‐ 50 μm thick, red line), and different grain concentrations and sample thicknesses for volcanic samples. The typical spatial resolution of the Quantum Diamond Microscope (1.2 μm) is indicated by the gray line.

There are 128 individual magnetic grains in our synthetic sample; this implies a concentration of $\sim$3,000 grains/${\mathrm{m}\mathrm{m}}^3$. The concentration in the natural volcanic sample is highly variable throughout the sample. For the four regions that we analyzed the concentration is $\sim$20,000 grains/${\mathrm{m}\mathrm{m}}^3$ (Table 1). When the entire microCT scan of the sample is considered, the average concentration is much higher: $\sim$72,000 grains/${\mathrm{m}\mathrm{m}}^3$ (de Groot et al., ²⁰¹⁸). Given the thickness of the samples (Table 1), we can calculate the theoretical amount of data points in a magnetic surface scan per variable to solve as a function of the resolution of the magnetic scan (Figure 6b). The spatial resolution of the MTJ scan was 10 μm, which was sufficient to determine individual magnetizations for grains in the synthetic sample (the red line in Figure 6b). For volcanic samples, however, the amount of data points per variable quickly drops to $<$10 for a spatial resolution of 10 μm, even for a sample that is “only” 30 μm thick. The MMT inversion struggles to determine the magnetizations of individual grains in this case, certainly if grains are physically not well separated in the sample. The spatial resolution that can be attained with the QDM set‐up, 1.2 μm (Glenn et al., 2017), yields $>$70 data points per variable, also for the volcanic sample configurations (Figure 6b). This provides the necessary amount of data points for a well‐posed MMT inversion. To summarize, while the MTJ technique is well‐suited for MMT inversions for samples with relatively low concentrations of magnetic grains, the QDM set‐up currently is the best magnetic scanning technique for MMT analyses on natural volcanic samples.

5.3. The Rock‐Magnetic Potential of MMT

The study of rock‐magnetic processes governing the acquisition and storage of complex magnetizations in Earth materials has kept track with the pace of technological advances in magnetic scanning techniques. In the 1980s and 1990s, the resolution and sensitivity of scanning magnetometry only allowed for characterizing magnetic domain configurations inside large magnetic grains. This was done by making Bitter patterns (e.g., Halgedahl, ¹⁹⁸⁷; Halgedahl, ¹⁹⁹¹), using the magneto‐optical Kerr effect (e.g., Ambatiello & Soffel, ¹⁹⁹⁶; Ambatiello et al., ¹⁹⁹⁹), or with magnetic force microscopy (e.g., de Groot, Fabian, et al., ²⁰¹⁴; Foss et al., ¹⁹⁹⁸; Pokhil & Moskowitz, ¹⁹⁹⁶, ¹⁹⁹⁷; Williams et al., ¹⁹⁹²). These studies yielded valuable insights into the way large iron‐oxides get and stay magnetized. Simultaneously, theoretical studies modeled the magnetic behavior of large iron‐oxide grains by taking a more fundamental approach to rock‐magnetism (e.g., Moon & Merrill, ¹⁹⁸⁴, ¹⁹⁸⁵; Xu & Merrill, ¹⁹⁸⁹, ¹⁹⁹⁰). More recent technological advances took magnetic imaging down to atomic scales. Both Electron Holography (e.g., Almeida et al., ²⁰¹⁴; Almeida, Muxworthy, Kovács, Williams, Nagy, et al., ²⁰¹⁶; Almeida, Muxworthy, Kovács, Williams, Brown, & Dunin‐Borkowski, ²⁰¹⁶; Feinberg et al., ²⁰⁰⁶; Harrison et al., ²⁰⁰²) and X‐ray photoemission electron microscopy (e.g., Bryson et al., ²⁰¹⁴; Nichols et al., ²⁰¹⁶) allow for a magnetic characterization at nm‐scale and yielded indispensable information on the internal magnetic behavior of naturally occurring minerals. The development of MERRILL, an open‐source software package for three‐dimensional micromagnetics (Conbhuí et al., 2018), enabled computationally assessing the magnetic behavior of relatively small ($<$1 μm) grains.

Despite the aforementioned progress, the interpretations of magnetic surface scans were still often two‐dimensional, relied on an upward continuation (Blakely, 1995; Fu et al., ²⁰²⁰; Lima & Weiss, ²⁰⁰⁹, ²⁰¹⁶; Lima et al., ²⁰¹⁴), or needed other additional assumptions. By adding a spatial characterization of the magnetic sources in the sample, the MMT technique overcame this classical inversion problem (Kellogg, 1929) and now allows for characterizing the three‐dimensional magnetic moment of individual grains inside a sample. It is important to emphasize that the magnetic surface scanning techniques used in this study are non‐destructive. MMT experiments can thus be repeated after laboratory treatments on the sample. This opens up entirely new venues for rock‐magnetic research: now the magnetic state of individual grains can be assessed as a function of magnetic treatment, size, shape, and possibly chemistry. This will lead to valuable insights into which grains are capable of recording the Earth's magnetic field and retaining that information over geologic time, and which grains should be avoided.

Building on a recent proof of uniqueness for microCT assisted potential field inversions using spherical harmonics (Fabian & de Groot, 2019), it was shown that MMT also allows inverting for higher‐order descriptions of the magnetic state of individual grains in a sample (Cortés‐Ortuño et al., 2021). Beyond the dipolar magnetic moments, the quadrupole and octupole descriptions provide insight into the complexity of the magnetic stray fields of individual grains in a sample. While the non‐uniqueness of the classical potential inversion problem (Kellogg, 1929) once again implies that it is impossible to directly invert the internal domain structure of individual grains without further a priori constraints, the higher‐order descriptions of their stray field can help to assess the complexity of the internal magnetic structure of individual grains (Cortés‐Ortuño et al., 2021). This may eventually bridge the gap between magnetic imaging techniques and computational micromagnetic models, and enable the development of a comprehensive, fundamental theory for the processes governing the acquisition and preservation of magnetic signals in multi‐domain grains in the future.

5.4. The Paleomagnetic Potential of MMT

When we are able to identify which grains are good paleomagnetic recorders, and which are the bad ones, it becomes possible to use MMT to its full potential and obtain paleomagnetic information from only the most reliable recorders in a sample. The acquisition of magnetizations in iron‐oxides is a statistical process. For small, single‐domain grains the moments of $10^6$ to $10^8$ grains must be considered before the direction and intensity of the resulting magnetic moment represent the direction and intensity of the ambient magnetic field at the time of cooling (Berndt et al., 2016). When measuring bulk samples this happens implicitly, standard size paleomagnetic samples contain in the order of $10^8$ to $10^9$ magnetic grains and the bulk signal is a statistical ensemble of the magnetizations of all these grains together.

Berndt et al. (2016) used Néel's theory on thermoremanent magnetizations in single‐domain ferromagnetic minerals (Néel, 1949, ¹⁹⁵⁵) for their estimations. Single domain grains cannot optimize their internal domain structure, as larger multi‐domain grains can. During the acquisition of their magnetization multi‐domain grains statistically end up in a local energy minimum, with an associated domain configuration. But these grains have many possible local energy minima and domain configurations. Depending on the nature and strength of the imparting field, the local energy minimum more or less represents the imparting magnetic field. In our experiments to determine a magnetic direction from subsets of grains in our synthetic sample, we strongly magnetized our sample by giving it an IRM at 1 T. We showed that it is possible to obtain an average direction that is only $0.2°$ to $12.9°$ off of the direction of the applied field (Figures 2f and 3f), after selecting grains with low remanence ratios from 128 grains in the sample. The IRM acquisition is generally reported to be 100 times more efficient than TRM acquisition (e.g., Fuller et al., ¹⁹⁸⁸). This could imply that for TRMs in multi‐domain grains $10^4$ to $10^5$ grains may already provide meaningful paleomagnetic information derived from subsets of individual grains in a sample, although this is currently highly speculative.

To assess whether it is both empirically and computationally possible to use MMT to determine naturally occurring paleodirections and paleointensities we assume that we need to sum the magnetic moments of ${\mathrm{10}}^5$ grains from a sample. With a concentration of 72,000 grains/${\mathrm{m}\mathrm{m}}^3$ in a volcanic sample (de Groot et al., ²⁰¹⁸) and a sample thickness of 50 μm, there are 3,600 grains per ${\mathrm{m}\mathrm{m}}^2$ of such a sample. This implies that 28 ${\mathrm{m}\mathrm{m}}^2$ of sample would be sufficient. This is challenging, but not impossible for our current magnetic scanning and microCT analyses. The current inversion routine, however, is not optimized for computational efficiency, yet. Hence, we are currently limited to invert only small parts of a sample (e.g., Figure 4), with low numbers of grains ($<$100). Moreover, the inversions were performed on a modest quad‐core desktop computer. By optimizing the code for a multi‐core machine and using a computational cluster it is possible to gain one to two orders of magnitude in speed. The computational demands can be further decreased by using the full potential of the recent proof of uniqueness for microCT assisted potential field inversions using spherical harmonics (Fabian & de Groot, 2019). A new inversion algorithm based on this concept promises to reduce the quadratic dependence of calculation time on the number of grains in the current inversion algorithm to an almost linear dependence, which will greatly reduce computational time. To summarize, ongoing developments allow for an increase of at least three orders of magnitude in computational speed. This would make it possible to invert for >$10^5$ grains and enables determining magnetic directions and intensities from individual grains in a sample.

A unique feature of MMT is the possibility to derive paleomagnetic information from subsets of grains in the sample. Here we used a rather crude selection criterion for the grains based on their remanence ratios. It is important to emphasize once more that the magnetic surface scanning techniques used in this study are non‐destructive. This implies that it is possible to mimic traditional paleomagnetic experiments such as step‐wise demagnetization, or paleointensity experiments while interpreting the magnetization of individual grains. Also, these traditional paleomagnetic experiments may provide additional information on how to discriminate between grains with good and bad magnetic recording properties, further testifying to the paleomagnetic potential of MMT.

6. Conclusions and Outlook

We showed that MMT is capable of determining magnetic moments of individual grains in both synthetic and natural samples using different magnetic scanning techniques. Thereby MMT is established as a paleomagnetic and rock‐magnetic technique and it opens up entirely new venues of paleomagnetic and rock‐magnetic research. Nevertheless, two significant challenges remain before MMT can be used to its full potential. First, the resolution of the microCT scan must be increased to detect all grains of interest, potentially down to the superparamagnetic threshold of $\sim$50 nm. Second, the computational power should become sufficient to solve for the large amounts of grains necessary for proper statistical analyses of the magnetic moments obtained for individual grains. When these two issues are resolved, MMT's unique ability to determine the magnetization of individual grains in a non‐destructive way will enable a systematic analysis of how naturally occurring iron‐oxides record and retain information on the past state of the Earth's magnetic field. These insights in which materials are reliable recorders of the ambient magnetic field and which should be avoided are vital for the paleomagnetic community, and adjacent communities using paleomagnetic data such as tectonic studies, studies of the deep Earth, and (magneto‐) stratigraphy.

By selecting only the contributions of known magnetically well‐behaved grains in a sample MMT enables obtaining reliable paleomagnetic information from even the most complex, crucial, or valuable paleomagnetic recorders. This includes lavas that form an indispensable archive of geomagnetic field variations. Fully unlocking this archive is vital for our understanding of the short‐term variability of the Earth's magnetic field. The potential of MMT, however, is not limited to lavas; paleomagnetic information from even more unique materials can also be retrieved. This includes e.g., the oldest rocks on Earth to shed light on the origin and evolution of the Earth's core; meteorites to unravel the conditions during the formation of our Solar system, and maybe even lunar samples to elucidate its origin and evolution.

Conflict of Interest

The authors declare no conflicts of interest relevant to this study.

Supporting information

Supporting Information S1

Table S1

Table S2

Movie S1

de Groot, L. V. , Fabian, K. , Béguin, A. , Kosters, M. E. , Cortés‐Ortuño, D. , Fu, R. R. , et al. (2021). Micromagnetic tomography for paleomagnetism and rock‐magnetism. Journal of Geophysical Research: Solid Earth, 126, e2021JB022364. 10.1029/2021JB022364

Data Availability Statement

The data presented in this manuscript are available in the PANGAEA.de repository: https://doi.pangaea.de/10.1594/PANGAEA.919360.