Abstract
Objective:
Deliverable proton spots are subject to the minimum monitor-unit (MMU) constraint. The MMU optimization problem with relatively large MMU threshold remains mathematically challenging due to its strong nonconvexity. However, the MMU optimization is fundamental to proton radiotherapy (RT), including efficient IMPT and proton arc delivery (ARC). This work aims to develop a new optimization algorithm that is effective in solving the MMU problem.
Approach:
Our new algorithm is primarily based on stochastic coordinate decent (SCD) method. It involves three major steps: first to decouple the determination of active sets for dose-volume-histogram (DVH) planning constraints from the MMU problem via iterative convex relaxation method; second to handle the nonconvexity of the MMU constraint via SCD to localize the index set of nonzero spots; third to solve convex subproblems projected to this convex set of nonzero spots via projected gradient descent method.
Main results:
Our new method SCD is validated and compared with alternating direction method of multipliers (ADMM) for IMPT and ARC. The results suggest SCD had better plan quality than ADMM, e.g., the improvement of conformal index (CI) from 0.56 to 0.69 during IMPT, and from 0.28 to 0.80 during ARC for the lung case. Moreover, SCD successfully handled the nonconvexity from large MMU threshold that ADMM failed to handle, in the sense that (1) the plan quality from ARC was worse than IMPT (e.g., CI was 0.28 with IMPT and 0.56 with ARC for the lung case), when ADMM was used; (2) in contrast, with SCD, ARC achieved better plan quality than IMPT (e.g., CI was 0.69 with IMPT and 0.80 with ARC for the lung case), which is compatible with more optimization degrees of freedom from ARC compared to IMPT.
Significance:
To the best of our knowledge, our new MMU optimization method via SCD can effectively handle the nonconvexity from large MMU threshold that none of the current methods can solve. Therefore, we have developed a unique MMU optimization algorithm via SCD that can be used for efficient IMPT, proton ARC, and other particle RT applications where large MMU threshold is desirable (e.g., for the delivery of high dose rates or/and a large number of spots).
1. Introduction
During pencil beam scanning (PBS) proton radiotherapy (RT), there exists a minimum threshold to the number of protons delivered per spot, which is measured in monitor unit (MU). The intensity modulated proton therapy (IMPT) subject to the minimum MU constraint is called the minimum-MU (MMU) optimization problem, i.e.,
| (1) |
where x denotes the spot weight (unit: number of protons or MU) to be optimized, g is the planning MMU, and F is the sum of planning objectives. The MMU constraint in Eq. (1) states that each entry of spot weight vector x is nonnegative, and no less than g if positive.
The MMU constraint in Eq. (1) reflects the physical limit that there exists a machine-specific MMU threshold Gmin. The purpose of Gmin is to control the machine delivery uncertainty within a desirable level, considering noise level of the monitor chamber, stability of the beam current and other factors [1]. Once Gmin is calibrated and set, the MU per spot must be at least Gmin in order for the spot to be deliverable on the machine.
Various methods have been developed to enforce the MMU constraint for deliverable PBS plans, including postprocessing methods [2–4] and optimization methods [5–9, 25].
However, instead of the physical MMU limit Gmin, a planning MMU threshold g with larger value than Gmin, i.e., g≥Gmin, is considered in the general MMU optimization problem Eq. (1), which is important for efficient IMPT [9], FLASH [10] and proton arc delivery [11].
The relevance of MMU optimization to efficient IMPT is owing to the proton physics that g is approximately proportional to the dose rate, and thus the IMPT plan optimized with larger MMU threshold g can be delivered more efficiently. However, MMU optimization with larger g is harder to optimize, and it is a tradeoff between plan quality and delivery efficiency for the MMU optimization. This tradeoff can be mitigated by increased optimization degrees of freedom from a constant MMU threshold (a scalar) for all energy layers to per-energy-layer MMU threshold (a vector) [9], in which g was optimized based on both delivery-time and plan-quality objective.
Besides the consideration of plan delivery efficiency, another important application of MMU optimization is for the FLASH RT, which requires the ultra-high dose rate for achieving biological dose sparing for normal tissues [10]. A new FLASH treatment planning method with MMU optimization, called Simultaneous Dose and Dose Rate Optimization (SDDRO), was proposed to maximize the dose rate and optimize the plan quality at the same time for FLASH [12]. However, the MMU optimization in SDDRO is to be improved, in the sense that the plan quality should not be worse, if more spots are included (e.g., with more beam angles).
The PBS delivery of proton arcs (ARC) is a new development that capitalizes more optimization degrees of freedom for better dose shaping and plan robustness [11]. Compared to IMPT with a set of a few beams (e.g., 2 to 4), the MMU optimization is especially important to ARC with a large number of spots from many beams. This is because ARC often involves much more optimization degrees of freedom, which results in generally much lower MU per spot. Consequently the optimization with the same MMU threshold can be much harder for ARC than IMPT, in terms of plan quality, especially when plan delivery efficiency is also of priority.
The MMU optimization remains challenging, because the MMU constraint and thus MMU optimization problem is nonconvex. And the nonconvexity increases as g increases, which occurs for efficient IMPT, FLASH, and ARC as discussed previously. To the best of our knowledge, current methods can only deal with the MMU problem with relatively small g, and none of them can provide a meaningful solution to the MMU problem with relatively large g, e.g., worse plan quality with more spots for optimization. Here we propose a stochastic coordinate descent (SCD) method for solving MMU optimization, and demonstrate its effectiveness for efficient IMPT and ARC, e.g., better plan quality with more spots.
2. Methods and Materials
Our MMU optimization algorithm consists of three components: (1) iterative convex relaxation (ICR) method to split out nonconvex dose-volume-histogram (DVH) constraints (Section 2.1) and nonconvex active spot set (Section 2.2); (2) stochastic coordinate descent (SCD) method to localize nonzero spots (Section 2.2); (3) projected gradient descent (PGD) method to solve the convex subproblem with respect to these nonzero spots (Section 2.3). The entire algorithm is summarized in Section 2.4.
2.1. Iterative Convex Relaxation (ICR)
The planning objective considered here is based on clinically used DVH constraints, which are nonconvex and handled by ICR [8,9,12].
We start with the notations: x the spot weight (unit: MU) and Nx the number of proton spots, d the dose distribution (unit: Gy) and Nd the number of dose voxels, D the dose influence matrix (unit: Gy/MU) and Dij the contributing dose from a unit jth spot to the ith voxel. That is,
| (2) |
Here Nx consists of spots on all energy layers from all beams, and the 3D dose distribution d is concentrated into a vector.
The general form of DVH constraints [13,14] consists of DVH max constraints (e.g., for organs-at-risk (OAR)) Eq. (3) and DVH min constraints (e.g., for planning target volume (PTV)) Eq. (4), where the region of interest (ROI) can be either OAR or PTV.
| (3) |
| (4) |
Given M constraints of constraint value c and weight w, the planning objective is
| (5) |
In Eq. (5), Ω is the active set of each constraint, which will be specified next. For each constraint, the least-square penalty will be active only in the subset Ω of the ROI.
To determine Ω of the ROI for a particular constraint, the dose d for this ROI needs to be first sorted to d′ in the descending order, i.e.,
| (6) |
This is because the DVH constraints Eq. (3) and (4) are specified in the form of “≥c dose”, which can be mathematically quantified based on d′ instead of d.
Then Ω can be determined for a DVH max constraint via Eq. (7) and a DVH min constraint via Eq. (8).
| (7) |
| (8) |
Where d′p is the dose (after sorting) corresponding to the volume p%, i.e., the minimum dose for the p% volume that receives the highest dose.
Note that Eq. (7) and (8) are analytic formulas that exactly solve the DVH constraints. Take a DVH max constraint for example: since the objective Eq. (5) is to minimize the least-square difference between d and c, Eq. (7) picks up the indexes of the least violation in d with respect to the constrained value c. Examples are provided in Appendix A to further illustrate DVH constraints and their solutions via Eq. (7) and (8).
On the other hand, Eq. (5) is general and also applies to other constraints [8,9]. For example, when applied to least-square and max/min/mean dose constraints, Ω is constant and includes the entire ROI.
For the convenience of method description, we rewrite the MMU problem Eq. (1) here
| (9) |
Here we define I0 as the set of all spots, since we will refer to subsets of I0 later.
F(x) in Eq. (9) is exactly specified by Eq. (5), which is formally denoted by
| (10) |
In Eq. (10), A consists of D, w, and Ω, and b consists of c, w, and Ω.
Once Ω is fixed, A linearly depends on D and w, b linearly depends on c and w, and Eq. (9) is a convex least-square problem, which can be conveniently solved. Here we use ICR [8,9,12] to deal with the nonconvexity coming from Ω owing to DVH constraints.
To simplify the presentation, we formally denote the determination of Ω from the dose d=Dx via Eq. (6)–(8) by Ω=H(d). Then the MMU optimization Eq. (9) via ICR contains two iterative steps (indexed by k): first to solve the MMU problem Eq. (11) with convex optimization objective as Ω is fixed in this step, and then update active sets Ω via Eq. (12) and subsequently the least-square term, i.e., Ak=A(Ωk) and bk=b(Ωk).
| (11) |
| (12) |
2.2. Stochastic Coordinate Descent (SCD)
Here we consider the MMU optimization subproblem Eq. (11), which is recapped here as
| (13) |
The MMU optimization Eq. (13) is nonconvex, because the MMU constraint is nonconvex. Because of nonconvexity, the iterative solutions from a straightforward optimization algorithm for solving Eq. (13), such as alternating direction method of multipliers (ADMM) [15–17], may not converge, especially with relatively large value of g.
To solve Eq. (13), we apply ICR one more time to split the MMU optimization into two iterative steps (indexed by m): first to select nonzero spot set I via SCD Eq. (14), and then to solve the convex subproblem restricted to I via Eq. (15).
| (14) |
| (15) |
The solution algorithm for Eq. (15) will be provided in the next section. In the following, we will describe the SCD method Eq. (14) for selecting nonzero spot set I.
To ensure that the optimization objective is monotonically decreasing during iterations, Eq. (14) is based on the SCD method. That is, we sweep over x in Nx iterations, and during each iteration, only a single spot x is optimized with the MMU constraint, while others are fixed. During the sweeping, each spot is solved only once, and the order of sweeping is randomized. Two benefits of SCD are: first it ensures the monotonic decreasing of optimization objective, and second each iterative step of solving a single spot has an analytic solution.
Moreover, due to the convexity of Eq. (15), the optimization objective is also monotonically decreasing during iterations, for a suitable optimization algorithm such as PGD in Section 2.3. Therefore, our optimization method with SCD and PGD together ensures the monotonic decreasing of optimization objective when solving Eq. (13).
For SCD, we denote aj as the jth column vector of A corresponding to xj, and then for a certain spot xn, we reformulate the least-square objective of Eq. (13) as
| (16) |
Then each SCD step (indexed by n) is the following MMU optimization with respect to a single spot xn′
| (17) |
Note that Eq. (17) has an analytic formula
| (18) |
That is, during the nth iteration, only the spot xn′ is updated via Eq. (18), while the rest spots are fixed, i.e.,
| (19) |
Here, to distinguish from n, n′ denotes the randomized index of the spot to be updated during the nth iteration.
After the sweeping through all spots (i.e., in Nx iterations), the index set of nonzero spots of the final iterate of Eq. (19) is taken to be the nonzero spot set I in Eq. (14), i.e.,
| (20) |
To summarize, the SCD algorithm solves for I in Eq. (14) using Eq. (19) and (20).
2.3. Projected Gradient Descent (PGD)
This section describes the PGD method [18] for solving the convex subproblem Eq. (15), which is rewritten as
| (21) |
with f(x)=‖Ax-b‖2 and admissible solution set C defined as
| (22) |
The solution algorithm to Eq. (21) via PGD is based on
| (23) |
where μ is the step size along the gradient of f and P is the projection operator onto the convex set C.
Note that the projection onto C via P is to solve the following optimization problem
| (24) |
which has an analytic solution
| (25) |
To summarize the PGD method, first a one-step gradient descent is calculated at current iterate xn, and then this is projected to C so that xn+1 remains admissible.
Here we also utilize a so-called momentum method [19] to accelerate PGD. In the momentum method, an auxiliary variable y is introduced, and a fraction γ from the current iterate yn carries over to the next iterate yn+1.
The accelerated PGD replaces Eq. (23) with two following steps
| (26) |
| (27) |
2.4. Overall Solution Algorithm
The overall solution algorithm for solving the original MMU problem Eq. (9) is summarized here for the convenience of implementation.
Algorithm parameters: K, γ, μ, and N.
Initialization: x0=0
for k=0 to K-1
Ωk+1 = H(Dxk),
Ik+1 = SCD(xk, Ωk+1)
xk+1 = PGD(Ik+1, Ωk+1, μ, γ, N)
end for
The above algorithm has three major steps: (1) nonconvex DVH constraints are handled by ICR in Step 4, which consists of Eq. (6)–(8); (2) nonconvex MMU constraint is handled by SCD in Step 5, which consists of Eq. (19) and (20) and subsequently provides nonzero spot set Ik+1; (3) convex MMU subproblem Eq. (15) restricted onto Ik+1 is solved in Step 6, which consists of Eq. (26) and (27).
The appearance of Ωk+1 in SCD (Step 5) and PGD (Step 6) reflects the dependence of optimization objectives on Ω, i.e., Eq. (5) and (10). The iteration loop of Eq. (11) and (12) indexed by k is combined with the iteration loop of Eq. (14) and Eq. (15) indexed by m, i.e., with a single index k in the above algorithm.
The parameters are set empirically in this study: K=20, γ=0.95, μ=1/|∥A∥, and the number of PGD iterations N=200. Note the parameters (γ, μ, N) are only needed for PGD in Step 6. The number of SCD iterations (Eq. (19)) is the same as the number of spots Nx. For efficient implementation of SCD, instead of calculating bn as the product of a matrix and a vector in Eq. (16), the difference between bn and bn-1 is calculated, which is essentially the product of a vector and another vector.
2.5. Materials
Our new algorithm (“SCD”) is validated in comparison with a state-of-the-art algorithm (“ADMM”) for MMU optimization with relatively large g. ADMM refers to our previously developed iterative convex relaxation algorithm [8,9] with inner loops solved by ADMM [15–17], which has been shown to be effective for solving a variety of treatment planning problems besides MMU optimization, including energy-layer minimization [8], dose-rate optimization [9,12,22,26], and hybrid proton-photon optimization [24]. Three clinical cases for treatment planning studies included a lung case (Table 4 and Fig. 4), a brain case (Table 5 and Fig. 5), and a prostate case (Table 6 and Fig. 6). In each case, ADMM and SCD were planned for the scenarios of efficient IMPT and ARC respectively.
Table 4.
Lung. The dosimetric quantities from left to right: optimization objective value, max dose of PTV, conformal index, mean dose and V20 of lung, mean dose and V30 of heart, mean dose of esophagus, cord, and body. The values of g are listed in Table 1.
| Unit: % | f | Dmax | CI | Lung | V20 | Heart | V30 | Eso | Cord | Body | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| IMPT | ADMM | 2.8 | 126 | 56 | 12.2 | 15.5 | 4.9 | 0.73 | 20.9 | 6.8 | 6.2 |
| SCD | 1.9 | 119 | 69 | 10.0 | 10.9 | 3.4 | 0.53 | 11.5 | 4.8 | 4.9 | |
| ARC | ADMM | 16.4 | 167 | 28 | 19.4 | 20.9 | 6.0 | 0.89 | 40.8 | 11.5 | 10.7 |
| SCD | 2.2 | 116 | 80 | 9.4 | 9.0 | 2.2 | 0.25 | 10.3 | 4.2 | 4.7 | |
Figure 4.
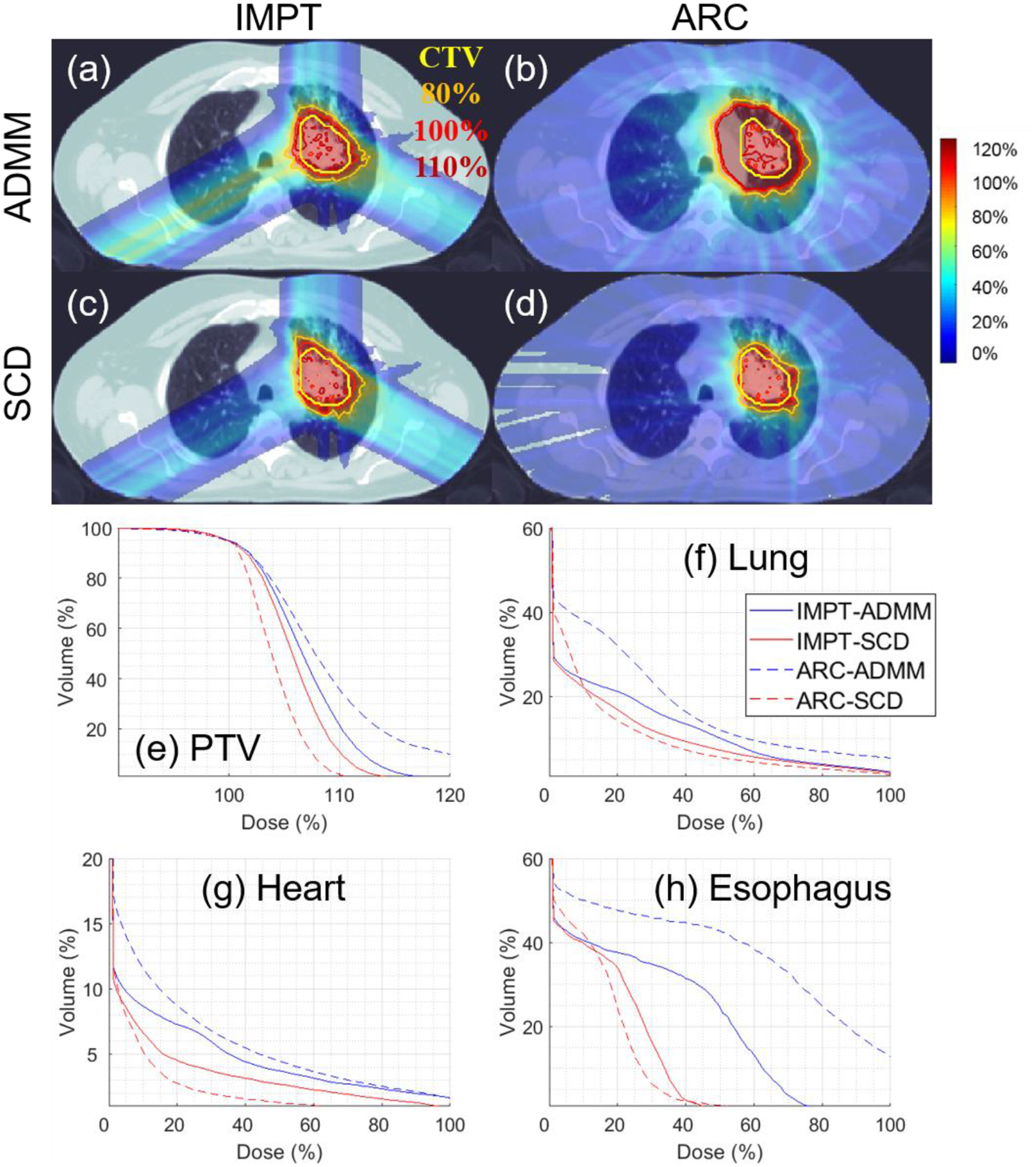
Lung. The dose plot window is [0%, 110%]. 110%, 100%, 80% isodose lines and PTV are highlighted in dose plots. The values of g are listed in Table 1.
Table 5.
Brain. The dosimetric quantities from left to right: optimization objective value, max dose of PTV, conformal index, mean dose and V10Gy of brainstem, V12Gy of brain, and mean dose of body. The values of g are listed in Table 1.
| Unit: % | f | Dmax | CI | BS | V10Gy | V12Gy | Body | |
|---|---|---|---|---|---|---|---|---|
| IMPT | ADMM | 9.2 | 130 | 24 | 20.3 | 7.9 | 22.4 | 2.0 |
| SCD | 3.1 | 119 | 70 | 18.7 | 4.1 | 8.6 | 1.1 | |
| ARC | ADMM | 99.1 | 214 | 9 | 26.0 | 6.3 | 36.9 | 4.6 |
| SCD | 3.9 | 117 | 63 | 16.4 | 1.0 | 6.1 | 1.1 | |
Figure 5.
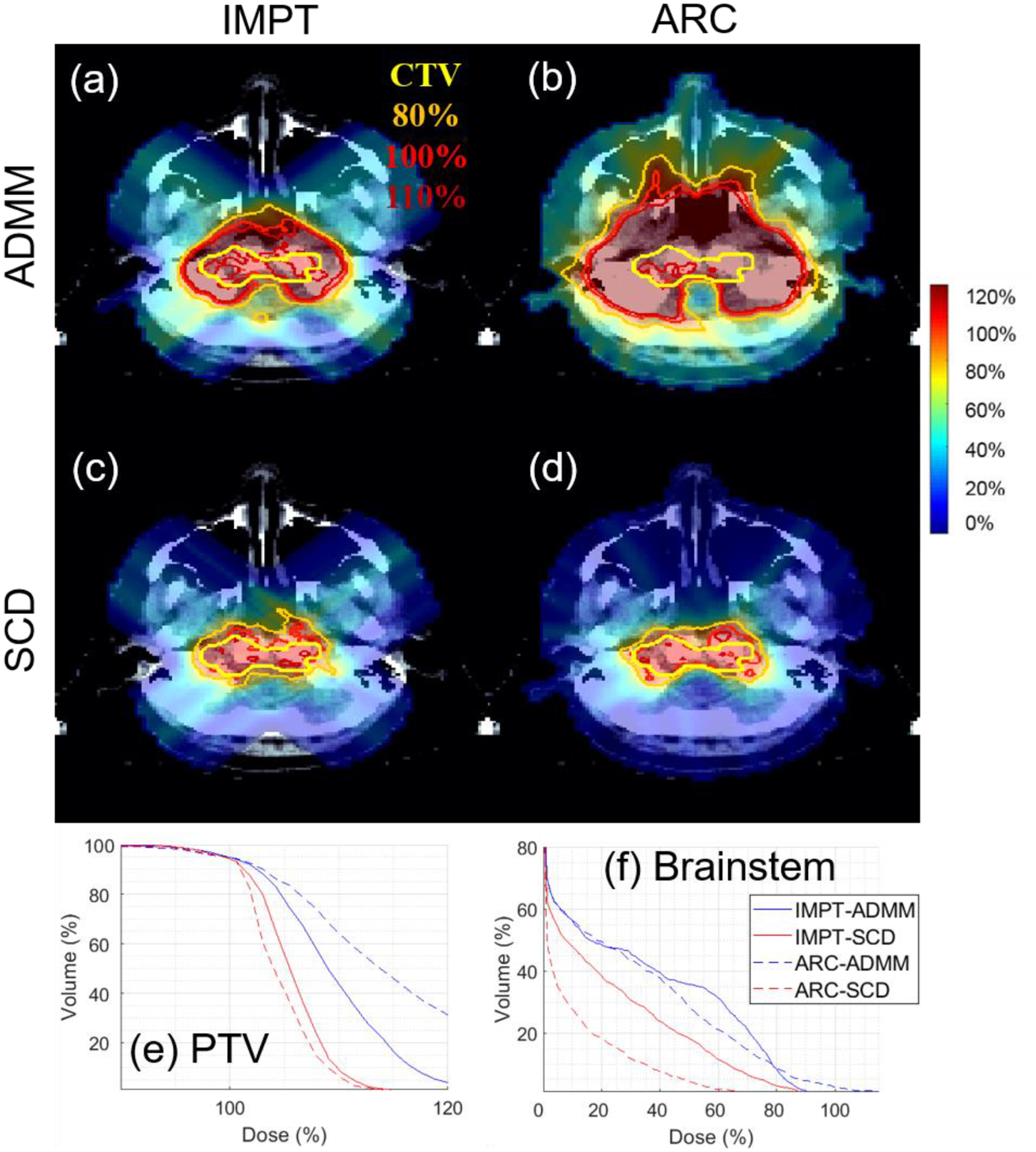
Brain. The dose plot window is [0%, 110%]. 110%, 100%, 80% isodose lines and PTV are highlighted in dose plots. The values of g are listed in Table 1.
Table 6.
Prostate. The dosimetric quantities from left to right: optimization objective value, max dose of PTV, conformal index, mean dose and D10 of bladder, mean dose and D10 of rectum, mean dose of femoral head, penile bulb, and body. The values of g are listed in Table 1.
| Unit: % | f | Dmax | CI | Bl | D10,Bl | Re | D10,Re | FH | PB | Body | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| IMPT | ADMM | 1.9 | 125 | 36 | 31 | 108 | 35 | 106 | 37 | 33 | 2.9 |
| SCD | 0.86 | 114 | 70 | 23 | 82 | 29 | 90 | 28 | 27 | 2.2 | |
| ARC | ADMM | 8.0 | 179 | 18 | 90 | 179 | 78 | 171 | 17 | 45 | 5.5 |
| SCD | 0.55 | 111 | 80 | 39 | 87 | 38 | 83 | 5.6 | 25 | 2.1 | |
Figure 6.
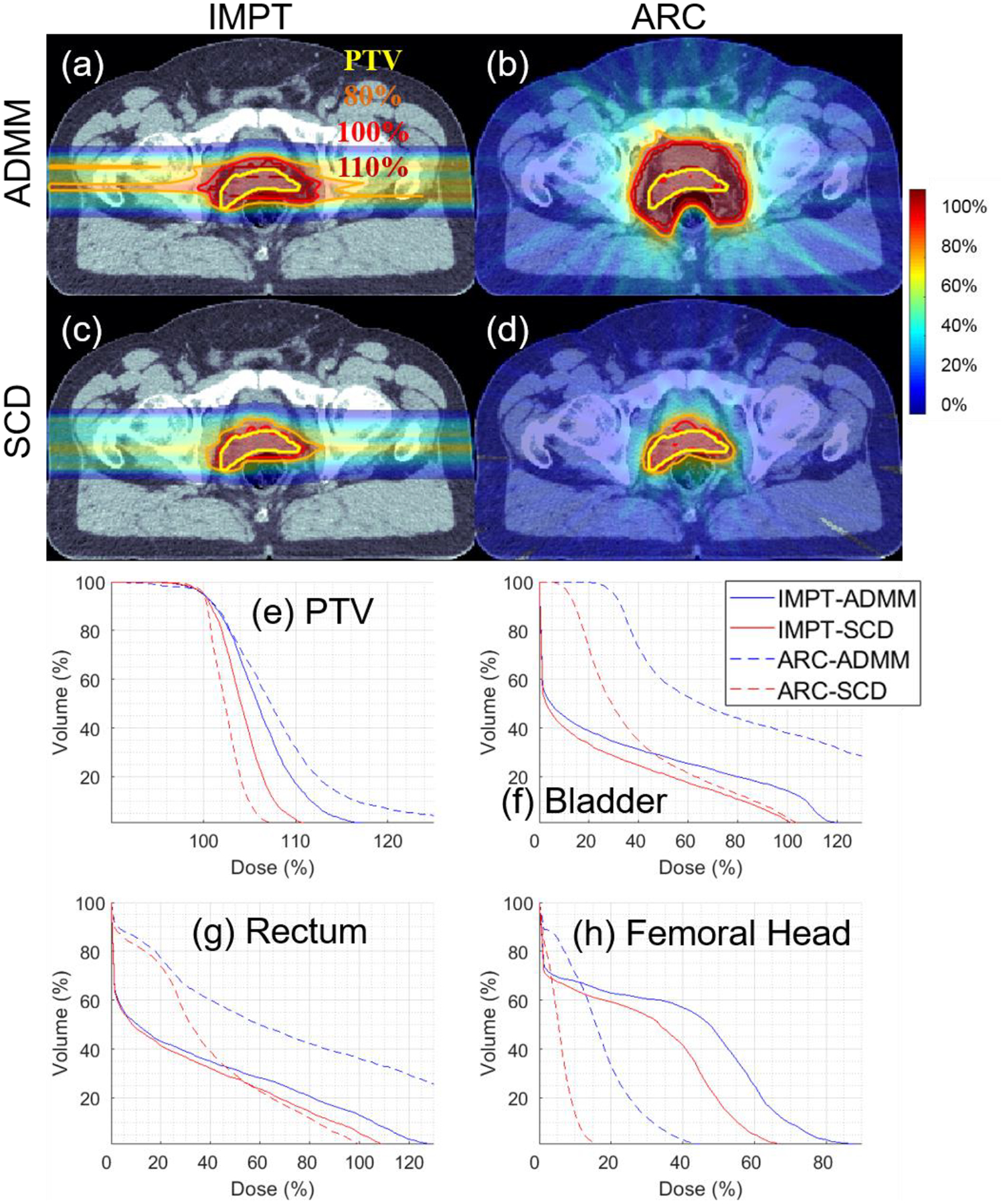
Prostate. The dose plot window is [0%, 110%]. 110%, 100%, 80% isodose lines and PTV are highlighted in dose plots. The values of g are listed in Table 1.
For completeness, we also compare ADMM and SCD with a post-processing method (“PP”) [2] and the spot-reduction method (“SR”) [25] under various values of g (Fig. 1), for brain IMPT (Table 2 and Fig. 2) and prostate ARC (Table 3 and Fig. 3). Varian Eclipse treatment planning system currently uses PP [2].
Figure 1.
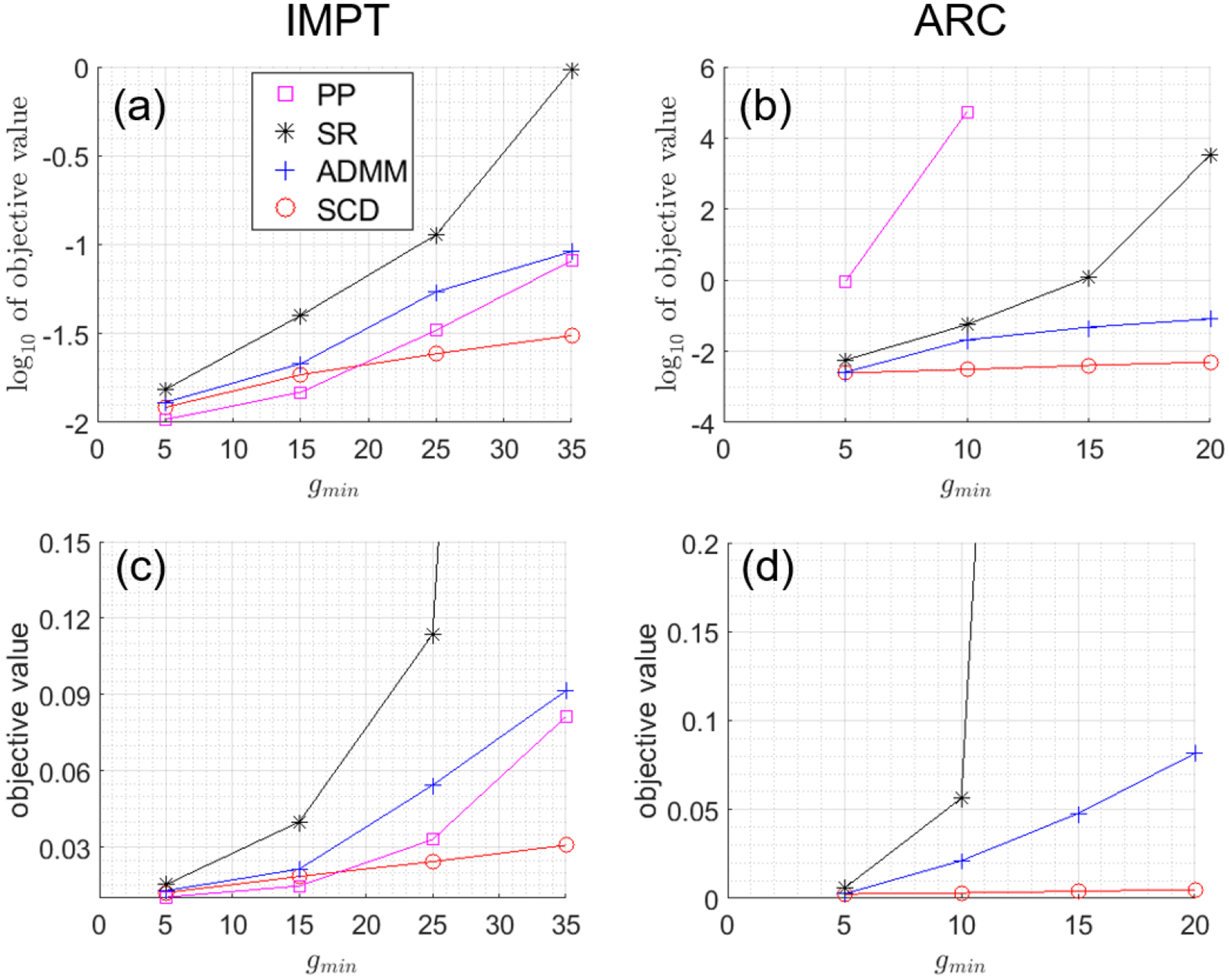
Optimized objective values with different g’s. (a) log10 of objective values for Brain IMPT; (b) log10 of objective values for Prostate ARC; (c) objective values for Brain IMPT; (d) objective values for Prostate ARC. Note that all spot weights are zero from PP and thus PP is not available at g=15 and 20 for Prostate ARC. The unit of g is 106 protons.
Table 2.
IMPT for brain with g=5. The dosimetric quantities from left to right: optimization objective value, max dose of PTV, conformal index, mean dose and V10Gy of brainstem, V12Gy of brain, and mean dose of body.
| Unit: % | f | Dmax | CI | BS | V10Gy | V12Gy | Body |
|---|---|---|---|---|---|---|---|
| PP | 1.5 | 112 | 85 | 17.0 | 2.0 | 5.8 | 0.8 |
| SR | 4.0 | 119 | 76 | 18.9 | 3.2 | 6.5 | 0.9 |
| ADMM | 2.1 | 116 | 79 | 18.3 | 3.3 | 6.8 | 0.9 |
| SCD | 1.9 | 112 | 81 | 17.5 | 3.6 | 7.2 | 1.0 |
Figure 2.
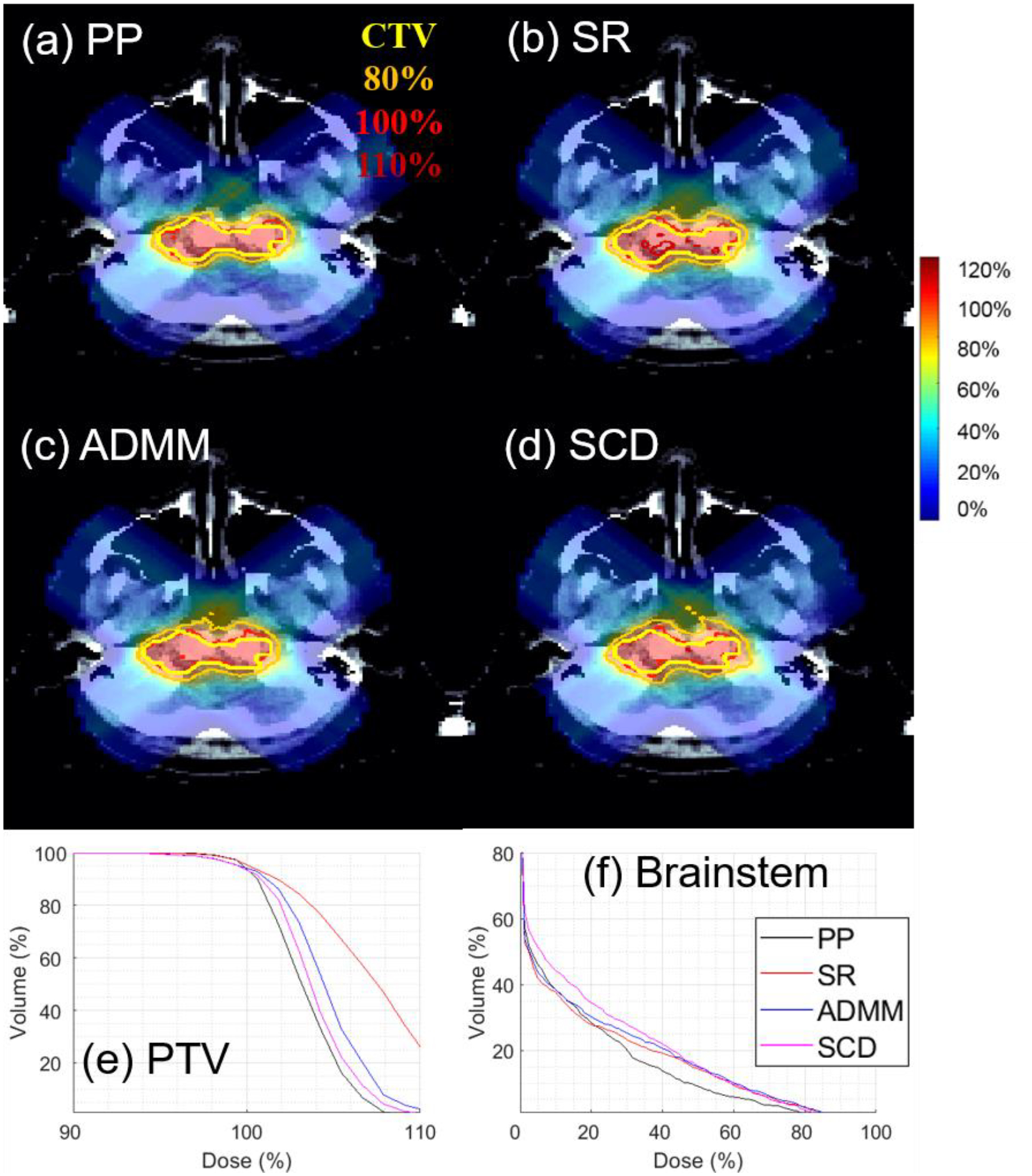
IMPT for Brain with g=5. The dose plot window is [0%, 110%]. 110%, 100%, 80% isodose lines and PTV are highlighted in dose plots.
Table 3.
ARC for prostate with g=5. The dosimetric quantities from left to right: optimization objective value, max dose of PTV, conformal index, mean dose and D10 of bladder, mean dose and D10 of rectum, mean dose of femoral head, penile bulb, and body.
| Unit: % | f | Dmax | CI | Bl | D10,B1 | Re | D10,Re | FH | PB | Body |
|---|---|---|---|---|---|---|---|---|---|---|
| PP | 90.0 | 199 | 43 | 37 | 102 | 31 | 92 | 5.1 | 43 | 2.2 |
| SR | 0.57 | 109 | 87 | 31 | 77 | 30 | 73 | 5.0 | 23 | 1.8 |
| ADMM | 0.26 | 107 | 92 | 27 | 74 | 25 | 68 | 4.1 | 22 | 1.5 |
| SCD | 0.24 | 103 | 90 | 34 | 82 | 33 | 76 | 5.2 | 25 | 1.9 |
Figure 3.
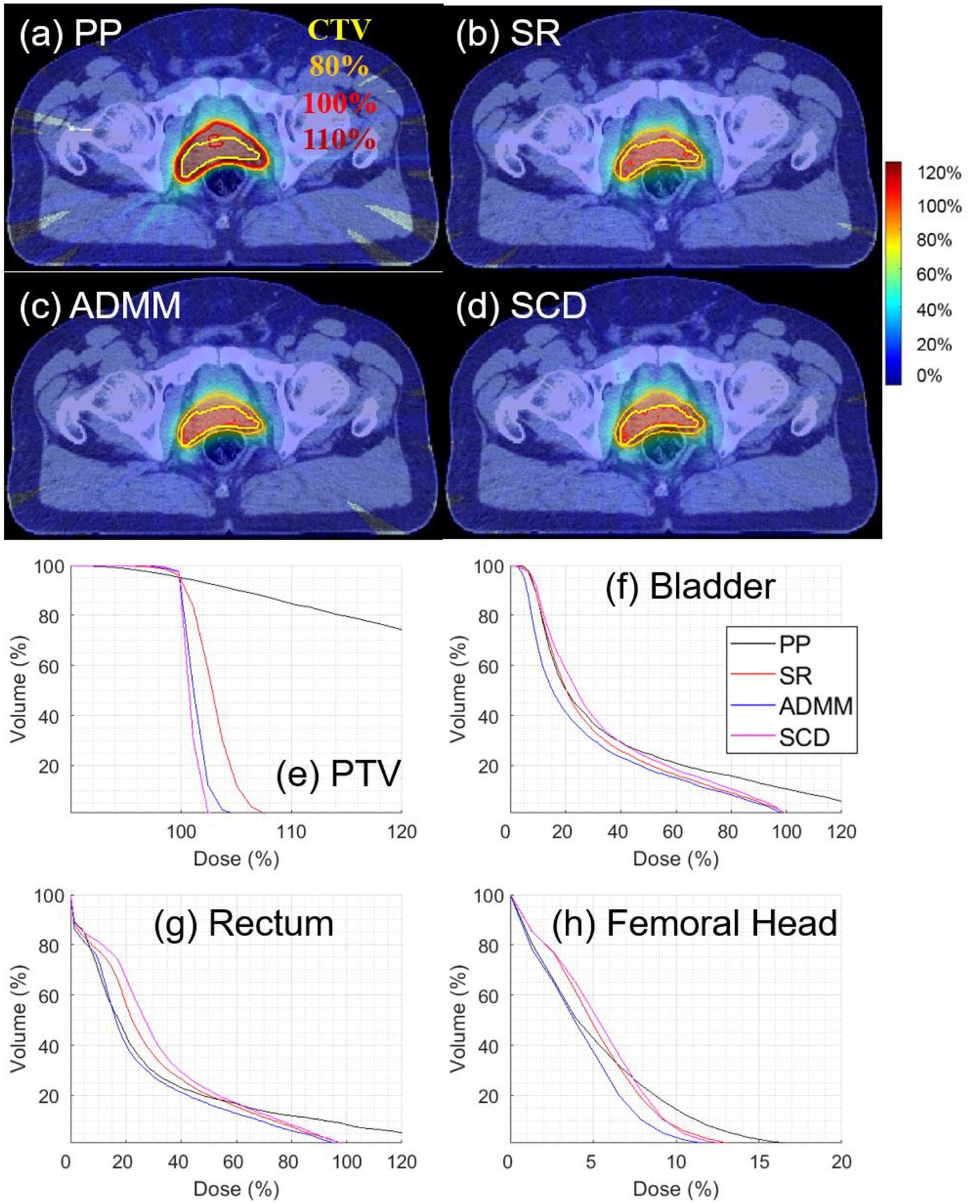
ARC for Prostate with g=5. The dose plot window is [0%, 110%]. 110%, 100%, 80% isodose lines and PTV are highlighted in dose plots.
PP first solves without the MMU constraint (i.e., g=0) and then generates the final spot weights via a post-processing rounding step with respect to g, which in this work is through
| (28) |
SR was developed by Paul Scherrer Institute [25] and can heuristically handle the MMU constraint by iterative removal of small-weight spots, i.e., the smallest m% spot weights are set to 0 every n iterations during a total of N iterations. In this study, m=10, n=50, N=300 for brain IMPT and m=20, n=20, N=100 for prostate ARC.
Clinically used DVH constraints were used for treatment planning. All plans were normalized to have D95=100% to PTV. Dose influence matrices D were generated via MatRad [20] with 5 mm spot width, and 3 mm lateral spacing on 3 mm3 dose grid. The beam angles for IMPT were empirically chosen to be (0°, 120°, 240°) for lung, (45°, 135°, 225°, 315°) for brain, and (90°, 270°) for prostate. All beam angles were used for ARC, which consisted of 24 beam angles sampled equally from 0° to 345°, without deliverability optimization of ARC. Relatively large values of MMU threshold g (i.e., with improved efficiency of plan delivery) were chosen to demonstrate the difference between ADMM and SCD (Table 1).
Table 1.
clinical cases with large g. The dosimetric quantities from left to right: dose per fraction (unit: Gy), number of fractions, MMU threshold (unit: 106 protons), number of proton spots, plan optimization time for ADMM (unit: second), and plan optimization time for SCD (unit: second).
| d | Nf | g min | Nx | TADMM | TSCD | ||
|---|---|---|---|---|---|---|---|
| IMPT | Lung | 2 | 30 | 30 | 6081 | 244 | 2400 |
| Brain | 2 | 10 | 35 | 2458 | 56 | 364 | |
| Prostate | 1.8 | 25 | 40 | 2339 | 170 | 920 | |
| ARC | Lung | 2 | 30 | 30 | 48646 | 417 | 7800 |
| Brain | 2 | 10 | 30 | 14644 | 92 | 660 | |
| Prostate | 1.8 | 25 | 20 | 27940 | 313 | 4630 |
In Table 2–6, the conformal index (CI) is defined as V1002/(V×V′100) (V100: PTV volume receiving at least 100% of prescription dose; V: PTV volume; Vʹ100: total volume receiving at least 100% of prescription dose). The value of CI is between 0 and 1, and ideally CI=1. All the quantities are in percentage: the dose quantities are in percentage with respect to the prescription dose; the volume quantities are in percentage with respect to total volume of the structure under consideration; optimized objective value f and CI are unitless and displayed in percentage for uniform presentation of results.
3. Results
3.1. Comparison with different g values
For small g value, i.e., g=5 in Fig. 1, all four methods had comparable objective values for IMPT, while SR, ADMM, and SCD had comparable objective values for ARC, which were smaller than PP. Dose and DVH plots are presented in Fig. 2 and 3 for IMPT and ARC respectively, while dosimetric parameters are presented in Table 2 and 3 respectively. Fig. 2 and Table 2 show that PP, ADMM, and SCD had comparable plan quality for IMPT, while SR had slightly degraded target coverage. Fig. 3 and Table 3 demonstrate SR, ADMM, and SCD had comparable plan quality for ARC, while PP had much worse plan quality, e.g., the target coverage in Fig. 4(a) and (e).
As g increases, SCD was more robust than ADMM, which in turn was more robust than PP and SR, in terms of preserving plan quality measured by objective values. Note that all spot weights were zero from PP and thus PP was not available at g=15 and 20 for ARC (Fig. 1(b)). Therefore, for large g value, we will only compare SCD with ADMM in the followings.
3.2. Efficient IMPT
The first application of MMU optimization with relatively large g considered in this work is for efficient IMPT (with a few beams).
In terms of the target coverage, Table 4–6 show that SCD is quantitatively better than ADMM: the CI improved from 0.56 to 0.69 for lung (Table 4), from 0.24 to 0.70 for brain (Table 5), and from 0.36 to 0.70 for prostate (Table 6); under the same target dose normalization, the max target dose decreased from 126% to 119% for lung, from 130% to 119% for brain, and from 125% to 114% for prostate. The improvement of target coverage via SCD is also illustrated by comparing dose plots in (a) and (c) of Figure 4–6, e.g., larger 110% isodose line in ADMM, and tighter 80% and 100% to PTV in SCD, and also DVH plots in (e) of Figure 4–6, e.g., blue solid (ADMM) v.s. red solid (IMPT) lines.
In terms of the OAR sparing, Table 4–6 demonstrate that SCD generally had lower OAR dose than ADMM. For example, compared to ADMM, SCD decreased mean lung dose from 12% to 10% (Table 4), brainstem V10Gy from 7.9% to 4.1% (Table 5), and mean bladder dose from 31% to 23% (Table 6). The improved OAR sparing via SCD is also evidenced by that the DVH curve from SCD (red solid lines) is generally under that from ADMM (blue solid lines) in OAR DVH plots (f)-(h) of Figure 4–6.
3.3. ARC
The second application of MMU optimization with relatively large g considered in this work is for ARC (with many beams from a full arc).
In terms of the target coverage, Table 4–6 show that SCD is substantially better than ADMM: CI improved from 0.28 to 0.80 for lung (Table 4), from 0.09 to 0.63 for brain (Table 5), and from 0.18 to 0.80 for prostate (Table 6). With respect to g under consideration, ADMM failed to generate an acceptable plan, e.g., the max target dose was 167%, 214%, and 179% respectively for lung, brain, and prostate; however SCD still performed well, e.g., with the max target dose 116%, 117%, and 111% respectively for lung, brain, and prostate. The substantial improvement of target coverage via SCD is also illustrated by comparing dose plots in (b) and (d) of Figure 4–6, and DVH plots in (e) of Figure 4–6, e.g., blue dotted (ADMM) v.s. red dotted (IMPT) lines.
In terms of the OAR sparing, SCD again had lower OAR dose than ADMM in general, e.g., the decrease of mean lung dose from 19% to 9% (Table 4), brainstem V10Gy from 6% to 1% (Table 5), and mean bladder dose from 90% to 39% (Table 6), and improved OAR DVH plots via SCD (red dotted lines) compared to ADMM (blue dotted lines) in (f)-(h) of Figure 4–6.
3.4. SCD v.s. ADMM
In addition to previous sections, the comparison of optimization objective values between ADMM and SCD also demonstrates the superior performance of SCD, in terms of comparable objective values between IMPT and ARC (Table 4–6).
In contrast, note that the plan quality of IMPT was better than that of ARC for ADMM, e.g., optimization objective value was 0.028 and 0.164 for IMPT and ARC via ADMM in Table 4. This shows that ADMM failed to handle nonconvex MMU constraint, because IMPT used a beam subset from ARC and therefore ARC (optimization with more degrees of freedom) should be no worse than IMPT in theory. In contrast, the comparison results of ARC and IMPT with SCD make physical sense, i.e., the plan quality of ARC was comparable with that of IMPT, e.g., optimization objective value was 0.0086 and 0.0055 for IMPT and ARC via SCD in Table 6. This suggests that SCD was effective in dealing with the nonconvexity from the MMU constraint.
4. Discussion
Although it has been shown that our new method via SCD can effectively handle the MMU optimization problem with large MMU threshold, SCD does not fully solve the MMU problem in the sense that it may break down as well for sufficiently large MMU threshold. This is due to the problem nature of nonconvexity from the MMU optimization. Despite its limitation, SCD is still clinically significant in the sense that it overcomes the limitation of current MMU optimization methods (e.g., ADMM) to a certain extent, when large MMU threshold is desirable, e.g., for the delivery of high dose rates (efficient IMPT, FLASH) or/and a large number of spots (ARC).
SCD is particularly important to ARC. First, this is because a large number of spots need to be optimized and delivered for ARC [11], which effectively increases the MMU threshold substantially from IMPT. Second, similar to the comparison of IMRT and VMAT, compared to IMPT, a primary advantage of ARC is its delivery efficiency, which further demands large MMU threshold for efficient delivery (similar to efficient IMPT via increasing MMU threshold and thus dose rate). It has been demonstrated SCD can successfully solve the ARC problem with relatively large MMU threshold, e.g., with improved plan quality from IMPT to ARC when more spots are available for optimization. In comparison, current methods (e.g., ADMM) fail to do so, in the sense that they cannot optimize a large number of spots for ARC, for which their plan quality is deteriorated to be unacceptable (e.g., Fig. 4–6(b)).
A limitation of ARC studies here is that the ARC deliverability [11] is not considered. However, this simplification is appropriate for the purpose of this work on the effectiveness of SCD for MMU optimization. On the other hand, deliverable arcs can be constructed directly based on the ARC plan of many stationary beams via an additional sequencing step, similar to the leaf sequencing algorithm [21] from fluence-based VMAT (with many stationary beams) to deliverable VMAT.
FLASH requires the ultra-high dose rate, which corresponds to ultra-high MMU threshold. In our previous FLASH studies [12,22], it was found that, for such ultra-high MMU threshold, the optimization with more angles can have worse plan quality. This is similar to what was demonstrated in Section 3.3, e.g., due to the nonconvexity of the MMU constraint, ARC with more optimization degrees of freedom can have worse plan quality than IMPT, unless an optimization algorithm (e.g., SCD) can handle the nonconvexity. A future study will be performed to investigate the impact of SCD for FLASH.
Planning to CTV with robust optimization is often preferred over planning to PTV for proton RT [23]. However, the primary focus of this work is to develop SCD and illustrate its effectiveness for dealing with the MMU optimization, which is independent from robust optimization. Thus, planning to PTV is considered in this work for simplicity and clarity. For clinical implementation, our previously developed robust optimization algorithms [24] can be incorporated for SCD.
The dose calculation engine from MatRad [20] used in this work is based on pencil beam dose calculation algorithm, which is known to have limited accuracy in certain scenarios [26]. Also, this work used the default machine data provided by MatRad, which will need to be replaced with the commissioning data for clinical use.
This work considers the MMU optimization problem with a constant MMU threshold (a scalar) for all energy layers. An alternative is to use per-energy-layer MMU threshold (a vector) [9], which has the benefit to alleviate the nonconvexity of the MMU problem. The proposed SCD method is general and should be applicable to per-energy-layer MMU threshold as well. The joint use of SCD and per-energy-layer MMU threshold may allow for better plan quality from the MMU optimization, which will be investigated in a future work.
On the other hand, although the MMU threshold g for treatment planning has a minimum machine limit Gmin, i.e., Gmin=5 in this work, it has no maximum limit, as long as the plan quality is acceptable. However, because the plan quality decreases as g increases, the value of g is mainly limited by the optimization algorithm. Besides SCD or per-energy-layer MMU threshold, higher dose per fraction also allows for the increase of g.
5. Conclusion
We have developed a new MMU optimization algorithm based on SCD. To the best of our knowledge, our new method can accurately solve MMU problems with strong nonconvexity coming from large MMU threshold that current methods fail to solve, and therefore can serve as the cornerstone of optimization engines for many important applications that cannot be accurately solved by current methods, such as the delivery of a large number of spots (e.g., ARC) or/and ultra-high dose rate (e.g., efficient IMPT).
Acknowledgment
The authors are very thankful to the valuable comments from anonymous reviewers. This research is supported in part by the NIH Grant No. R37CA250921.
Appendix A
In implementation, Eq. (7) and (8) are solved respectively by
| (A1) |
| (A2) |
where j′ is the index of d′ in the descending order. Next we provide two examples to illustrate how to solve DVH constraints via Eq. (A1) and (A2).
First, we consider a DVH max constraint D20%≤30%. The DVH curve in Fig. A1(a) does not meet this constraint, because D20%=45%>30%. Following Eq. (A1), we first find p* by solving Dp*=30%, and arrive at p*=31%. Then from Eq. (A1), Ω for the DVH curve in Fig. A1(a) is the following
| (A3) |
Note that Eq. (A3) selects the indexes (20% to 31%) of the least violation of the constrained value c=30%, while the indexes (<20%) with larger dose deviation from c (i.e., ≥45%) are not included in Ω. This is consistent with the optimization objective Eq. (5), i.e., this choice of Ω in Eq. (A3) minimizes Eq. (5). On the other hand, as long as the dose in Ω (20% to 31% volume as shown in Fig. A1(a)) is reduced to be ≤30%, the DVH constraint D20%≤30% will be satisfied.
Second, we consider a DVH min constraint D98%≥100%. The DVH curve in Fig. A1(b) does not meet this constraint, because D98%=97%<100%. Following Eq. (A2), we first find p* by solving Dp*=100%, and arrive at p*=95%. Then from Eq. (A2), Ω for the DVH curve in Fig. A1(b) is the following
| (A4) |
Note that Eq. (A4) selects the indexes (95% to 98%) of the least violation of the constrained value c=100%, while the indexes (>98%) with larger dose deviation from c (i.e., <100%) are not included in Ω. This is consistent with the optimization objective Eq. (5), i.e., this choice of Ω in Eq. (A4) minimizes Eq. (5). On the other hand, as long as the dose in Ω (95% to 98% volume as shown in Fig. A1(a)) is increased to be ≥100%, the DVH constraint D98%≥100% will be satisfied.
Figure A1.
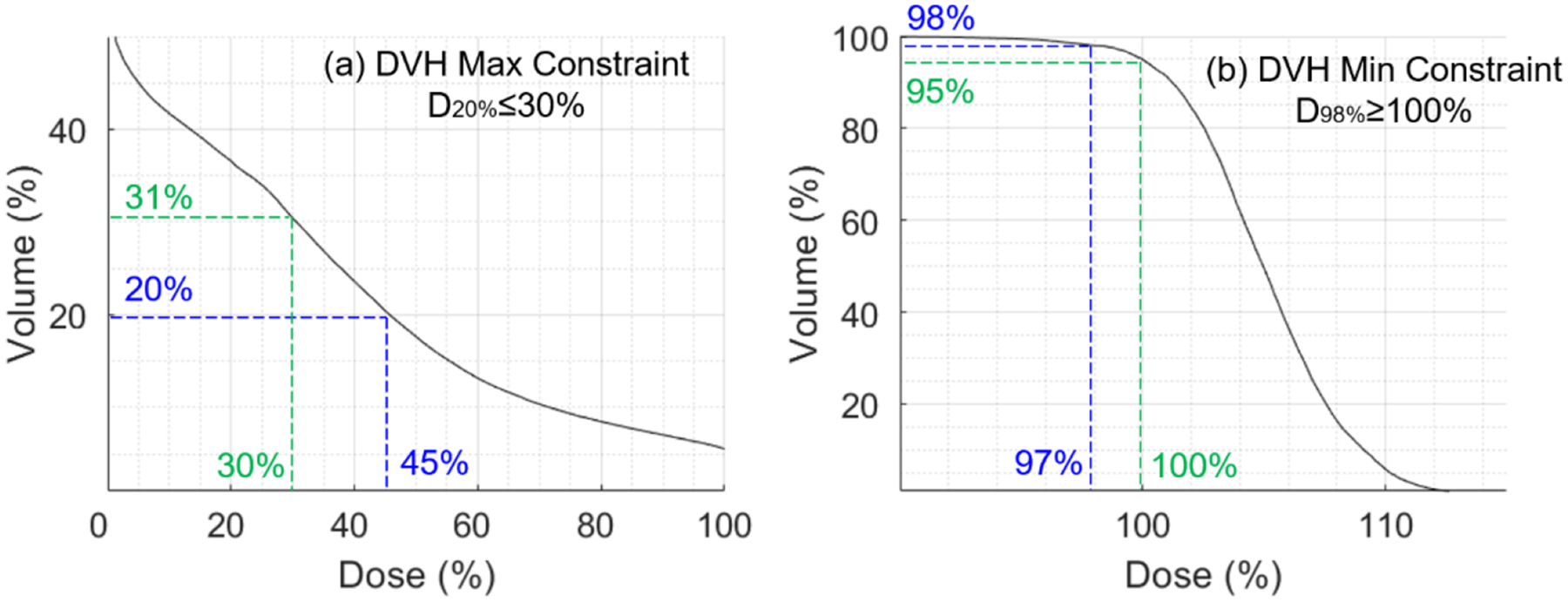
Examples of DVH constraints and Ω. (a) DVH max constraint; (b) DVH min constraint.
Footnotes
Ethical Statement: This research was carried out under Human Subject Assurance Number 00003411 for University of Kansas in accordance with the principles embodied in the Declaration of Helsinki and in accordance with local statutory requirements.
References
- [1].Clasie BM, Kooy HM and Flanz JB, 2016. PBS machine interlocks using EWMA. Phys Med Biol. 61, 400–412. [DOI] [PubMed] [Google Scholar]
- [2].Zhu XR, Sahoo N, Zhang X et al. , 2010. Intensity modulated proton therapy treatment planning using single-field optimization: the impact of monitor unit constraints on plan quality. Med Phys. 37, 1210–1219. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Lin Y, Kooy H, Craft D et al. , 2016. A Greedy reassignment algorithm for the PBS minimum monitor unit constraint. Phys Med Biol. 61, 4665–4678. [DOI] [PubMed] [Google Scholar]
- [4].Gao H, Clasie BM, Liu T et al. , 2019. Minimum MU optimization (MMO): an inverse optimization approach for the PBS minimum MU constraint. Phys Med Biol. 64 125022. [DOI] [PubMed] [Google Scholar]
- [5].Cao W, Lim G, Li X et al. , 2013. Incorporating deliverable monitor unit constraints into spot intensity optimization in intensity-modulated proton therapy treatment planning. Phys Med Biol. 58, 5113–5125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Howard M, Beltran C, Mayo CS et al. , 2014. Effects of minimum monitor unit threshold on spot scanning proton plan quality. Med Phys. 41, 091703. [DOI] [PubMed] [Google Scholar]
- [7].Shan J, An Y, Bues M et al. , 2018. Robust optimization in IMPT using quadratic objective functions to account for the minimum MU constraint. Med Phys. 45, 460–469. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Lin Y, Clasie BM, Liu T et al. , 2019. Minimum-MU and sparse-energy-level (MMSEL) constrained inverse optimization method for efficiently deliverable PBS plans. Phys Med Biol. 64, 205001. [DOI] [PubMed] [Google Scholar]
- [9].Gao H, Clasie BM, McDonald M et al. , 2020. Plan-delivery-time constrained inverse optimization method with minimum-MU-per-energy-layer (MMPEL) for efficient pencil beam scanning proton therapy. Med Phys. 47, 3892–3897. [DOI] [PubMed] [Google Scholar]
- [10].Wilson JD, Hammond EM, Higgins GS, et al. , 2020. Ultra-high dose rate (FLASH) radiotherapy: Silver bullet or fool’s gold?. Front Oncol. 9, 1563. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Ding X, Li X, Zhang JM, et al. , 2016. Spot-scanning proton arc (SPArc) therapy: the first robust and delivery-efficient spot-scanning proton arc therapy. Int J Radiat Oncol Biol Phys. 96, 1107–1116. [DOI] [PubMed] [Google Scholar]
- [12].Gao H, Lin B, Lin Y, et al. , 2020. Simultaneous dose and dose rate optimization (SDDRO) for FLASH proton therapy. Med Phys. 47, 6388–6395. [DOI] [PubMed] [Google Scholar]
- [13].Bortfeld T, Stein J, and Preiser K, 1997. Clinically relevant intensity modulation optimization using physical criteria. 12th Int. Conf. on the Use of Computers in Radiation Therapy. 1–4. [Google Scholar]
- [14].Wu Q, and Mohan R, 2000. Algorithms and functionality of an intensity modulated radiotherapy optimization system. Med Phys. 27, 701–711. [DOI] [PubMed] [Google Scholar]
- [15].Boyd S, Parikh N, Chu E, et al. , 2011. Distributed optimization and statistical learning via the alternating direction method of multipliers. Foundations and Trends® in Machine learning. 3, 1–122. [Google Scholar]
- [16].Goldstein T, and Osher S, 2009. The split Bregman algorithm for l1 regularized problems. SIAM J Imaging Sci. 2, 323–343. [Google Scholar]
- [17].Gao H, 2016. Robust fluence map optimization via alternating direction method of multipliers with empirical parameter optimization. Phys Med Biol. 61, 2838–2850. [DOI] [PubMed] [Google Scholar]
- [18].Bubeck S, 2015. Convex optimization: Algorithms and complexity. Foundations and Trends® in Machine learning. 8, 231–357. [Google Scholar]
- [19].Polyak BT, 1964. Some methods of speeding up the convergence of iteration methods. USSR Comput Math & Math Phys. 4, 1–17. [Google Scholar]
- [20].Wieser HP, Cisternas E, Wahl N. et al. , 2017. Development of the open-source dose calculation and optimization toolkit matRad. Med Phys. 44, 2556–2568. [DOI] [PubMed] [Google Scholar]
- [21].Craft D, McQuaid D, Wala J, et al. , 2012. Multicriteria VMAT optimization. Med Phys. 39, 686–696. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Lin Y, Lin B, Fu S, et al. , 2021. SDDRO-Joint: simultaneous dose and dose rate optimization with the joint use of transmission beams and Bragg peaks for FLASH proton therapy. Phys Med Biol. 66, 125011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Paganetti H ed., 2016. Proton therapy physics. CRC Press. [Google Scholar]
- [24].Gao H, 2019. Hybrid proton-photon inverse optimization with uniformity-regularized proton and photon target dose. Phys Med Biol. 64, 105003. [DOI] [PubMed] [Google Scholar]
- [25].Albertini F, Gaignat S, Bosshard M. et al. , 2009. Planning and optimizing treatment plans for actively scanned proton therapy. Biomedical Mathematics Promising Directions in Imaging, Therapy Planning, and Inverse Problems. 1–18. [Google Scholar]
- [26].Gao H, Liu J, Lin Y, et al. , 2021. Simultaneous dose and dose rate optimization (SDDRO) of the FLASH effect. Med Phys. Accepted. [DOI] [PubMed] [Google Scholar]
- [27].Hong L, Goitein M, Bucciolini M, et al. , 1996. A pencil beam algorithm for proton dose calculations. Phys Med Biol. 41, 1305–1330. [DOI] [PubMed] [Google Scholar]


