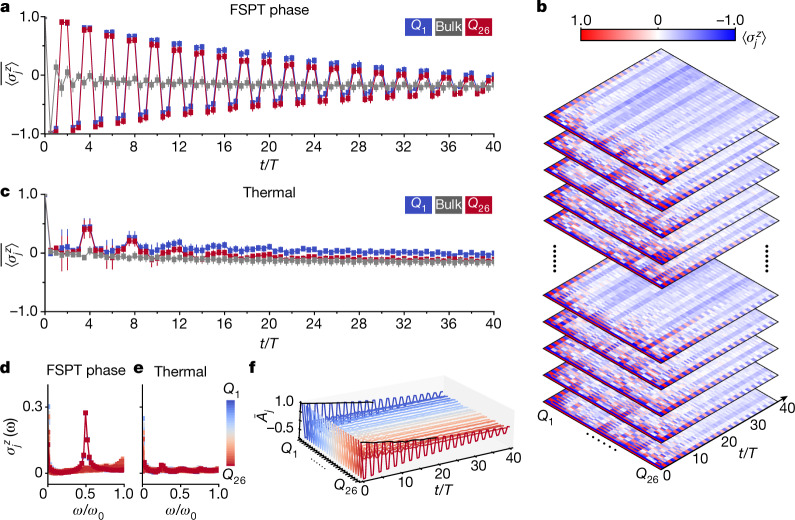
Fig. 2. Observation of an FSPT phase with 26 programmable superconducting qubits.

a, Time evolution of disorder-averaged local magnetizations deep in the FSPT phase (L = 26, J = Δ_J = 1, V = h = Δ_V = Δ_h = 0 and δ = 0.01). The initial state is ${|0⟩}^{\otimes L}$, and the data shown are averaged over 20 random disorder instances. The error bars represent the standard error of the mean over disorder samples. Whereas the bulk magnetization decays quickly to zero, the edge spins oscillate with a stable subharmonic response for up to 40 cycles. b, The evolution dynamics of local magnetizations for different random instances. Here each layer corresponds to a specific random instance. c, Magnetization dynamics deep in the thermal phase ( J = Δ_J = 1, V = h = Δ_V = Δ_h = 0 and δ = 0.8). d, Fourier transform of experimentally measured $\overline{⟨{\sigma }_j^z\left(t\right)⟩}$ in the FSPT phase. The edge spins lock to the subharmonic frequency, which is in sharp contrast to the bulk spins. e, Fourier spectra of $\overline{⟨{\sigma }_j^z\left(t\right)⟩}$ in the thermal phase. No robust subharmonic frequency peak appears for either edge spins or bulk spins in this case. f, Time dependence of the autocorrelator ${\overline{A}}_j=\overline{⟨{\mathrm{\Psi }}_0\left|{\sigma }_j^z\right(t\left){\sigma }_j^z\right(0\left)\right|{\mathrm{\Psi }}_0⟩}$ for up to 40 cycles, obtained from averaging over 20 random instances deep in the FSPT phase, with the initial states prepared as random product states in the computational basis. The black solid lines show the results of ‘echo’ circuits for the two boundary qubits.