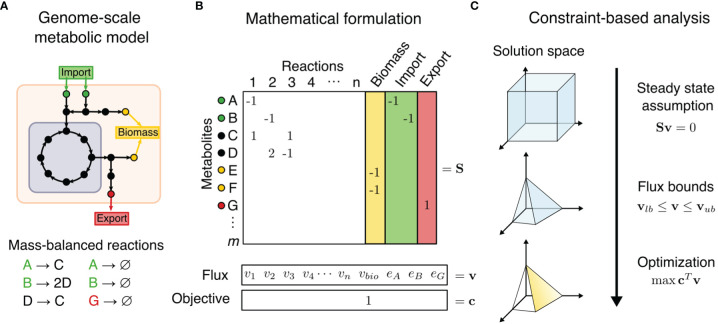
Figure 1.

Constraint-based metabolic modeling. (A) A genome-scale metabolic model is a compartmentalized network of mass-balanced reactions that convert products to reactants, and boundary pseudo-reactions that import or export metabolites. Biological objectives, such as biomass production, require activity through a subset of internal reactions. (B) The metabolic model is converted into a stoichiometric matrix (S) of size m × n, with rows representing m metabolites and columns n reactions. Reaction flux through all internal reaction (v_i ) and exchange reactions (e_i ) is represented by vector v of length n. Objective function Z = c ^T v is formulated as a linear combination of desired fluxes, weighted by vector c. (C) At steady state, the rate of production and consumption of a metabolite must be zero, which is described by the system of equations Sv = 0. There are many solutions to this system of equations, but the solution space can be constrained by imposing flux bounds (v _lb ≤ v ≤ v _ub ) and optimization such as maximization of objective function.