Physics of the Nuclear Pore Complex: Theory, Modeling and Experiment

Abstract

The hallmark of eukaryotic cells is the nucleus that contains the genome, enclosed by a physical barrier known as the nuclear envelope (NE). On the one hand, this compartmentalization endows the eukaryotic cells with high regulatory complexity and flexibility. On the other hand, it poses a tremendous logistic and energetic problem of transporting millions of molecules per second across the nuclear envelope, to facilitate their biological function in all compartments of the cell. Therefore, eukaryotes have evolved a molecular “nanomachine” known as the Nuclear Pore Complex (NPC).

Embedded in the nuclear envelope, NPCs control and regulate all the bi-directional transport between the cell nucleus and the cytoplasm. NPCs combine high molecular specificity of transport with high throughput and speed, and are highly robust with respect to molecular noise and structural perturbations. Remarkably, the functional mechanisms of NPC transport are highly conserved among eukaryotes, from yeast to humans, despite significant differences in the molecular components among various species.

The NPC is the largest macromolecular complex in the cell. Yet, despite its significant complexity, it has become clear that its principles of operation can be largely understood based on fundamental physical concepts, as have emerged from a combination of experimental methods of molecular cell biology, biophysics, nanoscience and theoretical and computational modeling. Indeed, many aspects of NPC function can be recapitulated in artificial mimics with a drastically reduced complexity compared to biological pores.

We review the current physical understanding of the NPC architecture and function, with the focus on the critical analysis of experimental studies in cells and artificial NPC mimics through the lens of theoretical and computational models. We also discuss the connections between the emerging concepts of NPC operation and other areas of biophysics and bionanotechnology.

1. Introduction

Eukaryotic organisms comprise one of the tree main branches of life, alongside with bacteria and archaea. Eukaryotic cells are highly morphologically and functionally diverse, and occur as unicellular micro-organisms (such as yeast) or as essential building blocks of tissues of complex organisms (such as humans). Nevertheless, they are universally characterized by the sequestration of their genome inside the cell nucleus (a feature from which they derive their name). This separation is achieved by a complex barrier of approximately 40 nm thickness, known as the nuclear envelope [1], which consists of two lipid membranes pierced or decorated by various proteins. The evolutionary origin of the nucleus and its subcomponents are still not fully understood [2,3]. Functionally, segregation of the nuclear DNA enables significantly more complex spatial and temporal regulation of intra-cellular processes compared to prokaryotes (e.g. bacteria), where the genome is directly accessible by most regulatory molecules [4]. On the other hand, sequestration of the DNA in the nucleus implies the need to regulate macromolecular transport across the nuclear envelope. Typical import cargoes include transcription factors, seeking access to the DNA in the nucleus, while typical export cargoes include mRNAs seeking access to the ribosomes in the cytoplasm [5]. Under normal operating conditions, millions of proteinaceous and nucleic acid molecules must cross the envelope per second in both directions [6].

All this multifarious bi-directional transport proceeds through molecular filtering “machines” termed nuclear pore complexes (NPCs) (see Figure 1). Altogether, several hundred to several thousands of NPCs perforate the nuclear envelope, depending on the cell type, with a typical flux of hundreds of molecules per second per NPC. Each transport event takes from several milliseconds to hundreds of milliseconds depending on the cargo type. In spite of the high throughput, molecular transport through the NPC is remarkably specific, rapid and robust with respect to molecular noise and structural perturbations [5,6,9].

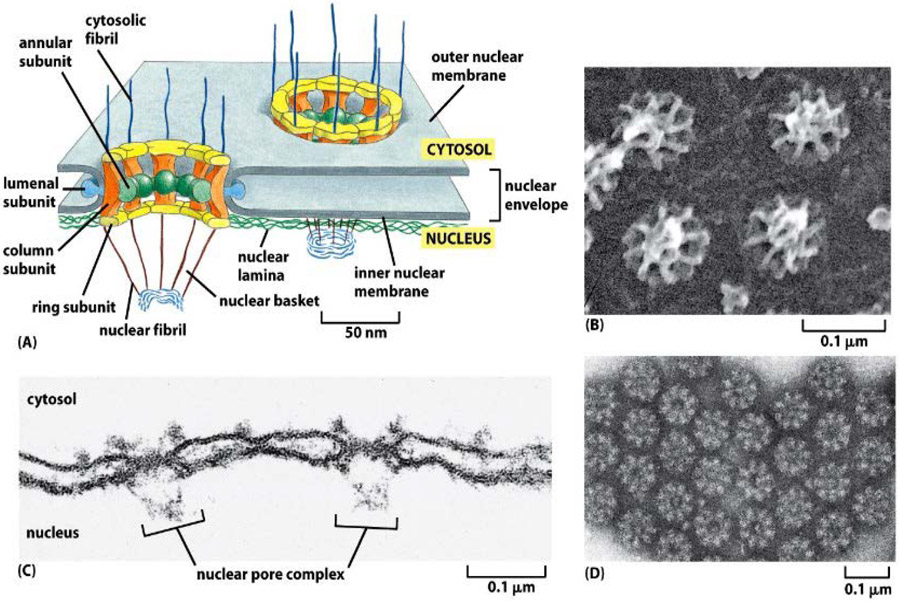
Figure 1.

(A) The nucleus is encapsulated by a nuclear envelope that comprises two lipid bilayers with an approximate overall thickness of 40 nm. NPCs perforate the nuclear envelope and mediate molecular transport between the nucleus and the cytoplasm. (B-D) Electron microscopy images showing nucleoplasmic, and cytoplasmic sides of a nuclear envelope of a Xenopus frog perforated by NPCs. Note the eightfold symmetry of the structure (D) and the nuclear basket structure (B,C) Reproduced from [1], permission pending.

As the sole conduit of nucleocytoplasmic transport, the NPC is a keystone component of multiple transport and regulatory processes in health and disease, such as gene regulation and signaling. Not surprisingly, dysregulation of NPC function is implicated in a number of diseases, from viral infections to cancer and neurodegenerative diseases [10-17].

The overall architecture and transport mechanism of the NPC is functionally conserved among species, although specific molecular details can vary [2,3,18-22]. Notably, many of the NPC properties have been recapitulated in vitro in simplified functionalized molecular assemblies and nanopore devices that mimic aspects of NPC architecture and function [23-28]. These observations suggest that NPC function relies on universal design features, and might largely be understood from fundamental physical principles.

The structure, architecture and functional mechanism of the NPC is unique amongst different cellular transporters [5,9], as detailed in the following sections. NPCs are assembled from multiple copies of approximately thirty different proteins termed nucleoporins. With a combined molecular mass of 60-125 MDa (depending on the species), NPCs constitute the largest macromolecular complexes in the cell [8,29,30]. In comparison, the ribosome, the protein synthesizing apparatus, is about two orders of magnitude smaller than the NPC. Approximately half of these proteins form a structure that perforates the nuclear envelope and forms the aqueous transport channel of the NPC. Recent structural studies using X-ray crystallography and electron microscopy/tomography, as well as mass-spectrometry and cross-linking, have provided detailed insights on how Nature assembles this giant “jigsaw puzzle” (Figure 2) [7,31-36].

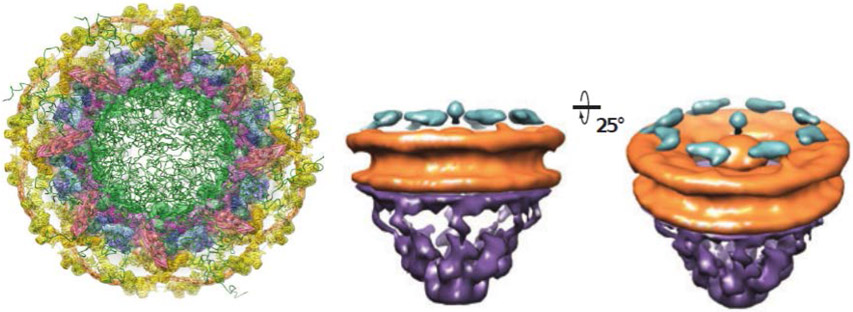
Figure 2.

Electron tomography structure of the NPC from different angles. The orange/yellow-labeled proteins form a ring-shaped structure that anchors the NPC to the nuclear envelope of the thickness of ~40 nm and that serves as the scaffold for the attachment of intrinsically disordered polypeptides, here schematically depicted in green. The purple structure is the nuclear basket. While the structure of the scaffold is now known to a high precision, the distribution of the intrinsically disordered domains in the passageway is much less defined. The diameter of the internal passageway is approximately 35-59 nm, and the overall length is ~100 nm, (including the basket). Note that the cytoplasmic filaments are not well resolved. Adapted from [7] and [8], permission pending.

The internal structure of the transport channel is equally unique. Its walls are decorated with multiple nucleoporins that contain highly flexible and dynamic intrinsically disordered regions (IDRs), which form the transport environment within the NPC passageway (IDRs are also known as natively unfolded or “unstructured” protein domains) [5,6,9,37-41]. The disordered nature of the nucleoporins within NPC passageway makes it challenging to experimentally probe their behavior at the relevant nanometer length and millisecond time scales. A major drawback arises from the high spatial and temporal mobility of the IDRs making them largely inaccessible to classical methods, such as X-ray crystallography and (cryo)-electron tomography, as these rely on ensemble averaging of individual conformations to obtain structural information. Although alternative techniques, such as atomic force microscopy (AFM), super-resolution microscopy , intra-cellular FRET and fluorescence correlation spectroscopy, have started to resolve the morphology and the dynamics of the transport channel in intact NPCs [42-48], much of our knowledge about the nuclear pore still derives from in vitro studies of its components and their assemblies, interpreted via computational and theoretical models. As a result, computational and theoretical modeling have been a key part in understanding the role of the intrinsically disordered protein domains in the NPC function.

Theoretical models have enabled rigorous investigation of various ideas and concepts of NPC function, facilitating quantitative interpretations of experimental data and providing predictions to guide the development of future experiments. To develop an adequate description of the NPC machinery, ongoing efforts have drawn upon a rich combination of ideas, theoretical concepts and simulation techniques. These span equilibrium and non-equilibrium statistical mechanics, stochastic process theory, polymer physics, and simulation techniques ranging from explicit atomistic molecular dynamics to coarse grained polymer models [49-63]. In combination, biophysical techniques and theoretical approaches are starting to reveal fundamental insights into the organization and the dynamics of the NPC at the nanoscale.

Besides its fundamental biological importance, the NPC also has served as a case study for the application of physical approaches to understanding of noise-dominated phenomena that occur in highly fluctuating nanoscale macromolecular assemblies in extremely complex biological molecular complexes. This review describes the recent advances in the understanding of the NPC, with the focus on the physical concepts, approaches and tools. In Section 2, we introduce the main structural and functional features of the NPC. Section 3 describes our current understanding of the biophysics of the interactions between the transport proteins and the intrinsically disordered proteins of the NPC, and how these interactions shape the internal morphology of the NPC passageway. Section 4 deals with the kinetics and dynamics of the NPC transport, based on the discussion on Section 3. We conclude with discussion in Section 5.

2. Biological function, molecular components and architecture of the NPC

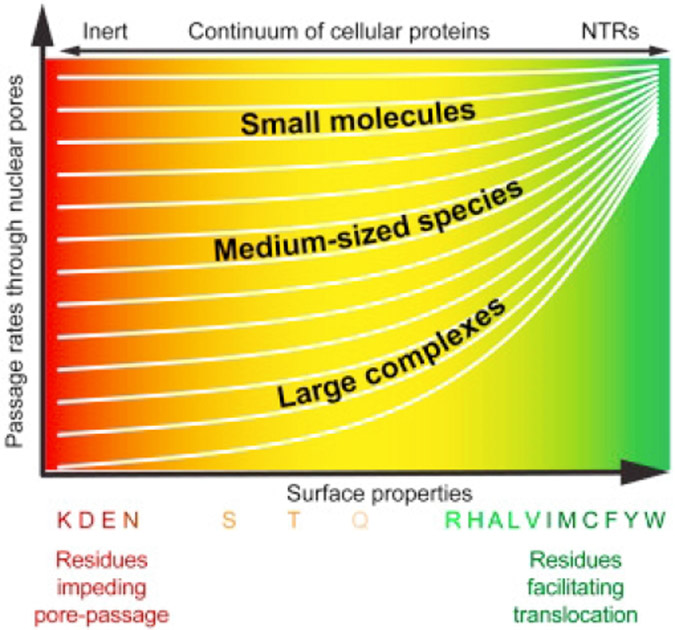
NPC is capable of transporting a variety of cargoes of different sizes and molecular characteristics [5,6,9,12]. These range from small molecules, such as ions, proteins such as transcription factors and histones, to large protein complexes, such as proteasomes, ribosomal subunits, and messenger RNAs (mRNA); the latter are exported from the nucleus packaged with proteins into what are known as messenger ribonucleoproteins (mRNPs) and can reach the size of tens of nanometers [64-66]. This transport versatility makes the NPC stand out from other cellular transporters such as ion pumps, metabolic transporters and porins, which are typically highly specialized to transport specific molecules [1]; consequently, it also stands out in terms of size and transport mechanism. One of the most striking and unique characteristic of the NPC is its ability to combine this transport versatility with high selectivity, throughput and relative robustness to structural perturbations [5,6,67-69].

The NPC is anchored to the nuclear envelope by a structural scaffold that forms a passageway with an inner diameter of about 35-50 nm (depending on the species) as illustrated in Figure 2 and Figure 3. Recent advances in electron tomography, X-ray crystallography and mass spectroscopy have resulted in the models of the pore scaffold approaching atomic resolution [7,31-35,70,71]. The structure of the scaffold will not be the focus of this review.

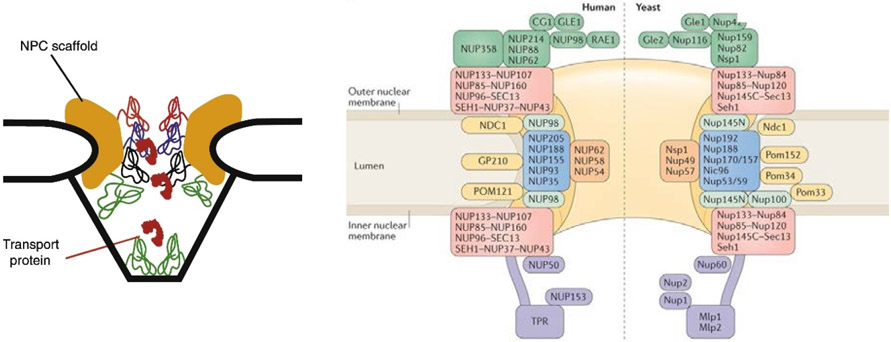
Figure 3.

Schematic rendering of the NPC structure. Left: Schematic illustration of the NPC cross-section. Yellow color denotes the structural scaffold of the NPC embedded in the nuclear envelope. Wriggly lines of different color denote different FG nups. Transport proteins are indicated in red. Adapted from [56], permission pending. Right: Schematic diagram of the locations of various molecular components of the NPC. The major human FG nups are Nup98, Nup62, Nup153 and Nup214. The major yeast FG nups are Nup100, Nup116, Nsp1, Nup1 and Nup2. Adapted from [31], permission pending.

The passageway of this pore is lined by numerous proteins that possess intrinsically disordered regions (IDRs) that are rich in hydrophobic Phenylalanine(F)-Glycine(G) amino-acid “patches” from which they derive their name - FG nucleoporins or FG nups, in short [5,72]. These proteins are end-grafted to the inner walls of the pore typically via small folded terminal domains [5,9]. Unlike the more familiar structured proteins, the intrinsically disordered regions of the FG nups do not fold into defined three-dimensional structures. Hence, in many respects they behave as conventional polymers [37,39,53,56,57,73,74]. We return to the molecular and the biophysical description of these molecules below. Each NPC contains about 200-300 FG nups per pore, spread among 10-15 different types that can differ in their amino acid sequence and localization within the NPC [9,10,19,22]. These chain-like molecules create a milieu within the NPC passageway that enables transport of a wide variety of cargoes through the same pore in both directions. This reliance on disorder also implies that, unlike other transporters, the NPC does not possess a gate that transitions between well defined “closed” and “open” conformations during a transport event.

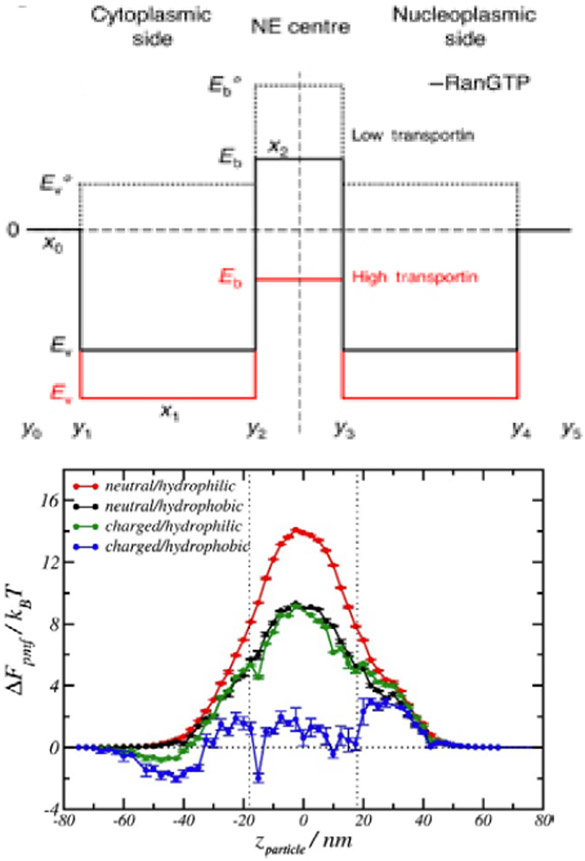
Despite this versatility, NPC is strictly selective and efficiently limits the transport only to appropriate cargoes. This combination of flexibility and selectivity of transport through the NPC is achieved through a two-layer regulation of transport specificity and kinetics. This is illustrated in Figure 4 for the example of the nuclear import cycle, which concentrates cargoes such as transcription factors inside the nucleus [6,9].

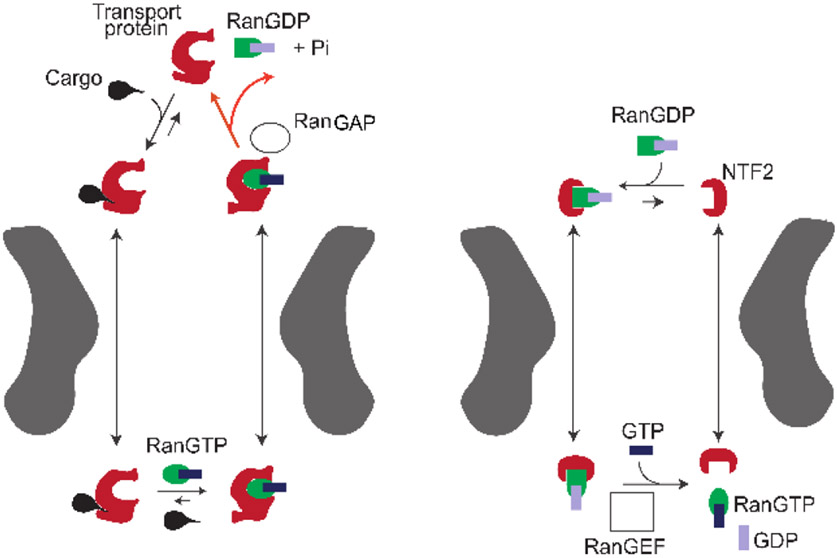
Figure 4.

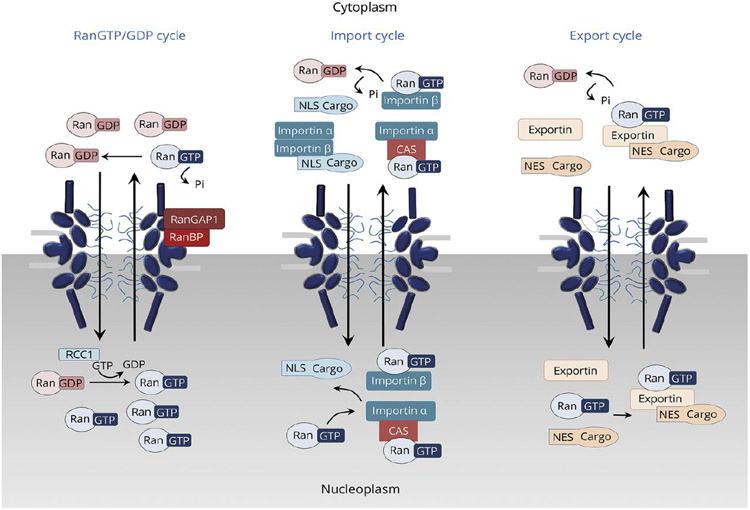
Schematic illustration of the import cycle of the NPC. Left: Cargo import cycle. Right: Ran cycle. See text for explanation. With the exception of GTP hydrolysis by RanGAP in the cytoplasm (red arrows), all the processes are thermodynamically reversible. Additional details are provided in Section 4.3. Adapted from [6], permission pending.

The first level of import regulation involves the binding of macromolecular cargoes in the cytoplasm to soluble transport proteins known as Importins/Transportins or Karyopherins (depending on the species); or more generally as nuclear transport receptors (NTRs). Throughout this review we will refer to them either as “transport proteins” or NTRs interchangeably. The function of these transport proteins is to recognize and bind specific cargoes in the cytoplasm through a short peptide motif on the cargo known as the nuclear localization sequence (NLS). The binding of cargoes to transport proteins can be regulated through the use of adaptor proteins, conformational changes and chemical modifications of the cargo (such as phosphorylation), thereby providing the first layer of regulation of cargo recognition and transport [5,9,10].

The second layer of transport selectivity relies on multiple but relatively weak binding interactions between the transport proteins with the FG nups, which facilitates the entry and the eventual translocation of the cargo-NTR complex through the NPC passageway [9]. By contrast, the NPC hinders the entry and translocation of macromolecules that do not bind to the transport proteins and do not bind directly to the FG nups: whereas ions and small molecules (up to a few nanometers) like ATP can freely translocate through the NPC by diffusion, larger molecules and particles are progressively hindered from entering and translocating through the NPC with increasing size [75-77].

Inside the NPC passageway, the translocation of transport protein/cargo complexes is primarily a diffusive process, driven by thermal fluctuations and facilitated by the interactions with the FG nups [6,78-80]. Each individual translocation of a transport protein/cargo complex occurs without requiring direct input of energy, e.g., in the form of ATP or GTP hydrolysis, and typically takes on the order of several milliseconds [78,81]. Yet, macroscopically, NPC translocation is a part of the transport cycle that operates as a thermodynamic pump that concentrates cargoes inside the nucleus against their chemical potential gradient. Once the transport protein/cargo complex reaches the nucleus, the cargo is released from the transport protein through binding of the transport protein with RanGTP, which acts as a molecular switch that unilaterally releases the cargo from the transport protein (and thus from the NPC) into the nucleus [79,82]. The RanGTP-bound transport protein is free to translocate back to the cytoplasm, as illustrated in Figure 4 [6,9]. In addition, RanGTP is also known to catalyze the release of some of the transport proteins from the FG nups located at the nuclear basket, further enhancing the transport efficiency [43,80,83,84].

In the case of nuclear import, cargo concentrates in the nucleus at higher levels than in the cytoplasm (e.g. [85-89]), which ultimately requires the input of energy provided by the hydrolysis of a Ran bound GTP molecule and the accompanying conversion of RanGTP to RanGDP. This non-equilibrium step of the import cycle occurs in the cytoplasm, catalyzed by the cytoplasmic protein RanGAP (an abbreviation of “GTPase activating protein”). The energy obtained from the hydrolysis is used to overcome the binding of Ran to the transport protein, resulting in their detachment. After the release, the transport protein becomes available to bind the next cargo for nuclear import. Notably, in the operational NPC transport cycle, energy input in the form of GTP hydrolysis is not directly coupled to any molecular rearrangement of the NPC, unlike in many other familiar molecular motors and pumps (such as processive motors, ion exchangers, and ATPases) [90].

As a consequence, the nuclear import cycle scheme shown in Figure 4 uses one molecule of GTP and exports one Ran molecule from the nucleus to the cytoplasm per each cargo transported to the nucleus. (For transport proteins, such as Importin-β that use an adapter, Importin-α, to bind the cargo, the energy cost is two GTP molecules [5]). To maintain the concentration gradient of RanGTP across the nuclear envelope and thus the transport directionality, RanGDP needs to be shuttled back to the nucleus and converted back to GTP, as follows. Firstly, a specialized transporter, nuclear transport factor 2 (NTF2), re-imports the RanGDP molecule into the nucleus through a reversible energy-independent diffusion-based translocation through the NPC. There, GDP in RanGDP is substituted by GTP – a process catalyzed by the nuclear protein by Ran guanine exchange factor GEF (RanGEF; also known as RCC1) using GTP available in the cell. Importantly, with the exception of the GTP hydrolysis at the NTR release stage, all other transport and binding processes in the cycle are thermodynamically reversible. In summary, GTP hydrolysis powers the directional flow of cargoes into the nucleus that is rectified by the asymmetry in RanGAP and RanGEF localization between the nucleus and the cytoplasm. We return to the energetics and directionality of nuclear transport in Section 4.3.

As mentioned above, a most remarkable feature of the NPC is its ability to combine high transport selectivity with high speed of transport. Individual protein import/export events typically occur on millisecond time scales [78,81,91], and the transport times of even very large cargoes such as mRNPs are typically on the sub-second scale [66,92,93]. Notably, unlike other transporters, NPC translocation is not restricted to only one cargo at a time. Instead, the passageway of the NPC is typically crowded with multiple transport proteins, some of which are bound to cargoes and others not, some directed towards the cytoplasm, others to the nucleus. Overall, each NPC can contain hundreds of transport proteins at any given time, while transporting hundreds of cargoes per second [7,43,83,85]. It remains puzzling that the NPC can maintain its selectivity and its continuous, fast, parallel and bidirectional transport, in spite of this crowding.

Another remarkable aspect of NPC transport is its robustness with respect to deletion of its components. While several pore-specific constituent proteins are indispensable for cell viability and NPC transport functionality, a substantial fraction of the FG nups can be deleted (in yeast), resulting in no to mild defects in transport functionality [41,67,68,94]. In another manifestation of this structural robustness, transport defects caused by deletion of barrier-forming FG nups in one species (Xenopus) could be rescued by expression of functionally homologous FG nups from another species (yeast) [94].

Faced with this complexity, a number of different models have evolved in the field to address different aspects of NPC operation, ranging in focus from the general principles of the molecular transport on the nanoscale as revealed in in vitro NPC mimics, to the emphasis on the particular molecular mechanisms and structures as central to NPC transport [49,50,84,95-103]. Based on these ideas, the combined experimental and the theoretical work of the last decade has started to provide a comprehensive physical picture of NPC organization and function, within which molecular details and functional principles fall into place.

This review focuses on and elaborates this physical picture, with the emphasis on the following key questions about the NPC:

• What key physical principles and variables capture NPC function and how do they relate to the molecular architecture?

• What is the spatial organization of the FG nups inside the NPC passageway, and how does it define the transport properties?

• How can NPCs combine high selectivity with high speed and throughput in bi-directional transport under highly crowded conditions?

• How can the design principles of the NPC be mimicked and exploited by artificial nano-devices for protein sensing, sorting and transport?

3. Physics of the intrinsically disordered proteins of the Nuclear Pore Complex and their interactions with transport proteins

3.1. The gatekeeper of the NPC: FG nup assembly in the NPC

As mentioned above, the intrinsically disordered polymer-like FG nup domains are at the core of the NPC transport mechanism. Overall, the FG nup protein family contains 10-15 different subtypes that can vary in length and molecular sequence [5,7,9,41,62,63]. Within closely related species (such as vertebrates), individual FG nup types can have close homologues, but there can be large differences in sequence between distant species such as vertebrates and yeast [2,3,104]. In all species, the intrinsically disordered domains of these proteins harbor multiple hydrophobic Phenylalanine-Glycine (FG) repeat motifs in their sequence [5,6]. The FG motifs are typically interspersed by spacers that contain mostly neutral but also a small fraction of charged amino acids, typically with zero or slightly positive overall charge [10,63,101,105]. The FG repeats are an evolutionarily conserved motif of the FG nups, and they play a crucial role in the structure and function of the NPC. Generally, it has been noted that FG motifs commonly appear in the FG nup sequence either alone or in “patches” such as FGFG, FxFG or GLFG combinations, and occasionally as GF or single F amino acids. Although classification of the groups of FG nups based on these features has been discussed, the functional role of these differences is currently not fully understood [41,72,101,106] In current approaches, especially computational ones, the FG motif is commonly considered as the minimal “functional” unit responsible for the FG nup roles in NPC transport, but further studies are required. We return to this question in more detail in the following sections.

Most importantly, FG motifs are the main mediators of the interactions between the FG nups and the transport proteins, crucial for NPC permeability and selectivity, predominantly through hydrophobic interactions between Phenylalanines and hydrophobic grooves on the surface of the transport proteins [9,10,95,96,105-107]. FG motifs are also hypothesized to be largely responsible for intra- and inter-chain interactions between the FG nups, and thus potentially for shaping the morphology and the permeability of the FG nup assembly [97,101,108,109]. However, recent research shows that other interactions, such as electrostatic, cation-π, π − π can participate both in the interactions between FG nups and FG nup-transport protein interactions [63,67,96,105,110-112].

Functionally, FG nups play a twofold role: they form a template for the binding of cargo-carrying transport proteins in the NPC while simultaneously forming a permeability barrier against macromolecules that do not specifically bind the FG motifs. The exact nature of this barrier has been extensively debated, in particular whether it is based mainly on entropic forces [73,75,102,113] or whether it arises from breaking the attractive FG-FG interactions between the chains [97,109]. In general, the balance between the role of the chain entropy versus chain cohesion in the barrier has been unclear; and more recent studies emphasize that both are likely to play an important role [56,57,108,114].

3.2. Physics of FG nups on the single molecule level

FG nups, and IDRs in general, elude investigation by classical structural biology techniques, such as X-ray crystallography and electron microscopy because they lack a well-defined, ordered conformation [33,37,39]. Broadly speaking, at equilibrium the flexible IDRs populate a large ensemble of different conformations, much like classical polymeric molecules [39,115,116]. Although some disordered domains can retain a significant propensity for particular secondary structures [117,118]. the experimentally studied FG nups exhibit conformational ensembles that closely resemble polymer coils [73,101,103,119]. Accordingly, polymer physics concepts and tools have become key in elucidating the biophysics of IDRs and the FG nups. Experimentally observed FG nup behavior has been recapitulated in computational and theoretical models of different degrees of coarse-graining.

The conformational ensemble of a polymer-like molecule can be characterized by the moments of the spatial distribution of the monomer positions of the polymers [120,121]. Two variables that characterize the chain dimensions in space are widely used in the interpretation of experimental measurements: the average end-to-end distance R_E and the radius of gyration R_G. For a polymer of N monomers, with the monomer positions denoted as ${\overrightarrow{R}}_i$, these closely related quantities are defined as

$$R_E^2=\langle {\left({\overrightarrow{R}}_1-{\overrightarrow{R}}_N\right)}^2\rangle ,R_G^2=\frac{1}{N}{\sum }_{i=1}^N\langle {\left({\overrightarrow{R}}_i-{\overrightarrow{R}}_c\right)}^2\rangle$$ (1)

where ${\overrightarrow{R}}_c=\frac{1}{N}{\sum }_i{\overrightarrow{R}}_i$ is the coordinate of the geometrical center of the chain and the averaging ⟨…⟩ is performed over the distribution of the conformational ensemble of the polymer [120]. Closely related to R_G (within a factor of 0.7-1.4 [120,122]) is the hydrodynamic radius (also known as the Stokes radius) R_S, defined as $R_S=\frac{k_{B}T}{6\pi \eta D}$, where D is the diffusion coefficient of the molecule in space and η is the viscosity of the fluid.

As the name suggests, R_E is a measure of the average distance between the two ends of the polymer molecule, and R_G quantifies its average overall dimension in space. Experimentally, R_E can be inferred, for instance, from Förster resonance energy transfer (FRET) between fluorescent labels at the chain ends, and R_G by small-angle X-ray scattering (SAXS) [123-125]. The hydrodynamic radius of the chain R_S can be inferred from dynamic light scattering (DLS) [126] or/and from a comparison with reference proteins by size exclusion chromatography [101], as well as from conventional light scattering, analytical centrifugation and microfluidic diffusional sizing.

Generally, the average dimensions of polymer molecules in solution are determined by the balance between, on one hand, their ensemble entropy and inter-monomer steric repulsion within the chain (which favor more extended structures), and, on the other hand, attractive intra-chain interactions (which favor more compact conformations) [121,127-129]. Although classical polymer physics was largely developed for homopolymers – and FG nup sequences are quite heterogeneous – the insights from simple polymer concepts have turned out to be very helpful for the analysis and interpretation of FG nup behavior (and other disordered proteins) [39,56,57,73,101,108,130].

3.2.1. Theoretical background

In a simple classical Flory-type mean field theory [121,127], the free energy of a polymer chain of N monomers is

$$\frac{F(N,R)}{k_{B}T}\simeq \frac{R^2}{2b^{2}N}+f(n)R^3$$ (2)

where R is the size of the polymer coil in space, b is the monomer size and n is the average monomer density inside the chain n ≃ N/R³ . The first term roughly approximates the configurational ensemble entropy of a chain that performs a random walk in space, stretched to a size R [121]. The second term describes the free energy of a “gas” of monomers that is contained within the spatial volume occupied by the chain. In the spirit of the virial expansion, the free energy density is $f(n)\simeq \frac{1}{2}B{n}^2$ + higher order terms in n. The coefficient B is roughly proportional to the second virial coefficient of the monomer-monomer interaction [120,131]. It includes the steric repulsion between the monomers, also known as the “excluded volume” interactions, and attractive interactions that make B more negative. Microscopically, monomer-monomer interactions can arise from many molecular sources: hydrophobic, electrostatic and others, such as π − π and cation-π interactions between the aromatic rings of the Phenylalanines, as mentioned above. It is convenient to write it as B = ν₀(1 − χ_c) where ν₀ ~ b³ is the excluded volume of a monomer and χ_c characterizes the strength of the averaged self-cohesive attractive interactions within the chain, subsuming all molecular details; in the polymer physics literature, χ_c/2 is known as the Flory parameter [127]. The equilibrium chain size R is determined through the minimization of the free energy of Equation (2) with respect to R. The simple heuristic Flory theory can be derived using a number of different approximations using both lattice construction and continuous space. Although exact methods and simulations can modify the Flory theory predictions, in many cases it serves as a very good approximation, and has been the staple of the analysis of polymer chain behavior, and more recently protein IDRs [131,132].

At low average cohesiveness (small χ_c), the steric repulsion between the monomers dominates, and the polymer chain behaves like a self-avoiding random walk, adopting “relaxed coil” conformations at equilibrium [39,131,132]. In this regime the chain dimensions - both the R_G and R_E - scale with the chain length N as R ~ N^ν, where ν = 0.59. As the intra-chain attractive interactions increase (or, in polymer physics parlance, as the solvent quality decreases) the chains progressively become more compact and behave as Gaussian chains with ν = 0.5 at the point where repulsion and attraction are balanced. With a further increase in cohesiveness, the polymers undergo a smooth chain-globule transition to collapsed chains, with ν progressively decreasing to 1/3, characterizing the compact globular state [127,131,132]. Such scaling concepts have been extremely useful in the classification and analysis of IDR behavior. In the protein literature, more compact conformations are also known as “collapsed coils”, “molten globules” and “compact globules” [39,115,132].

3.2.2. Simulation approaches and methods

Investigated through computer simulations using Brownian and Langevin dynamics, as well as through various mean field and self-consistent field theories, simple homopolymer models have been a staple of the computational studies of the NPC and its components, and provided important insights into FG nup behavior [54,56,57,60,61,75]. Although lacking in molecular details, their significant advantages are flexibility, robustness of the predictions with respect to parameter choice, and speed, enabling to probe large spatial and long temporal scales.

At the opposite limit to simple homopolymer models, atomistic molecular dynamics (MD) simulations have the potential to give atomically resolved interaction profiles and conformational ensembles of FG nups [53,55,133-136]. However, these approaches have several pitfalls. First, current state-of-the-art atomistic simulations have difficulties probing timescales beyond several hundred nanoseconds to a microsecond in large multi-chain assemblies. This is significantly shorter than the millisecond transport events through the NPC, and much shorter than the timescales probed by coarse-grained models [137]. Beyond this technical limitation, the force fields used for atomistic MD simulations have been parametrized and optimized largely based on comparison with folded proteins. For IDRs, the ensembles predicted by atomistic simulations depend rather sensitively on the force fields and the water models used [138-141], and frequently appear more collapsed than experimental measurements [134,135]. Although modifications of the atomistic force fields have been proposed, this can lead to a certain degree of over-parameterization, and an accepted universal atomistic force field for IDRs is yet to be established [134,135,142,143].

Bridging between the completely “sequence-free” polymer models, and the atomistic models are chain models of intermediate coarse-graining levels that include some aspects of the sequence such as FG “patches” or hydrophobic or charged character of individual amino acids [59,62,63,144-146]. Although the coarse-graining procedure has not been standardized among different models, the salient predictions are commonly consistent between different computational realizations of FG nups.

3.2.3. Analysis of experimental data using theoretical and computational models

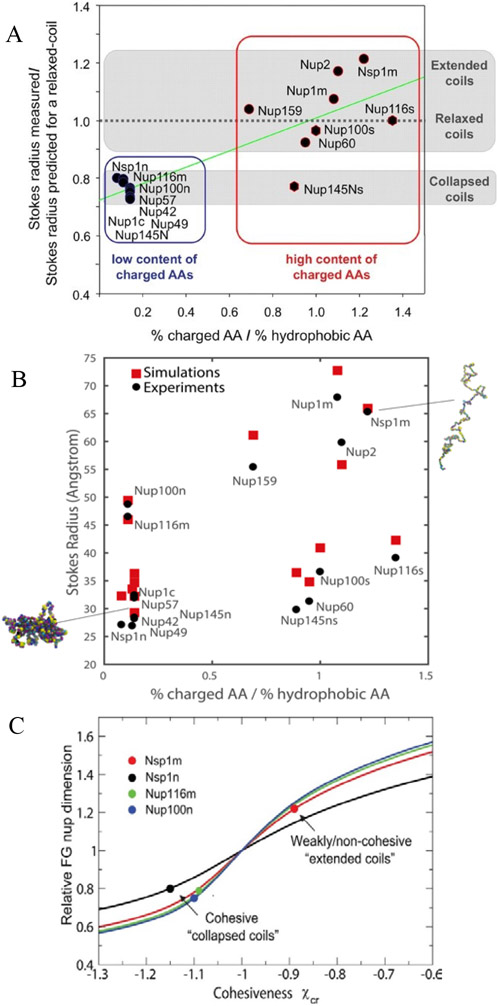
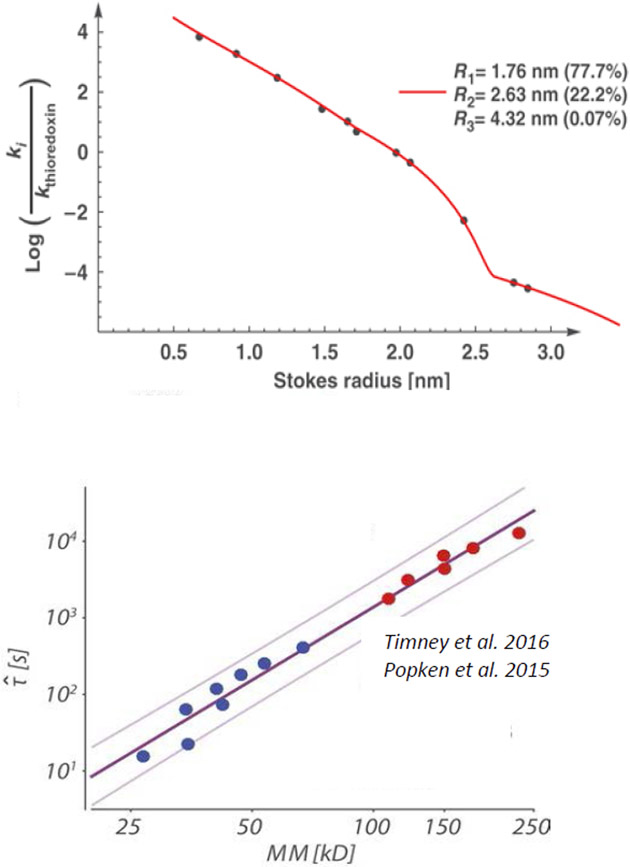
Dimensions of various FG nups were first systematically investigated by size-exclusion chromatography [101]. This provided estimates for the Stokes radii of various FG nup segments from Saccharomyces cerevisiae (yeast), and enabled comparisons with predictions for extended and collapsed polymer chains (Figure 5A). In brief, FG nup segments with more charged (and less hydrophobic) content showed more extended configurations (a regime that would correspond to ν > 0.5), whereas segments with more hydrophobic (and less charged) content had a more collapsed, cohesive character (regime that would correspond to ν < 0.5). These results come with the caveat that the interpretation of size-exclusion chromatography experiments is inherently complicated by the uncertainty in ascertaining the hydrodynamic radii of intrinsically disordered proteins moving through a gel. Analysis of these results using simple polymer models indicates that the chain cohesiveness, as expressed in the Flory parameter χ_c, roughly correlates with the ratio of the hydrophobic to charged content in the FG nup sequence [56]; see Figure 5C. In another work, differences in FG nup extension could be also accounted for via the differences in total vander-Waals volumes (and hence excluded volumes) of the amino acids in these sequences [74]. These observations are consistent with the general classification of IDRs according to their sequence composition [39,128]. A meta-analysis of a wider set of FG nups shows that on average, the FG nup dimensions agree with predictions for “ideal” Gaussian chains with ν = 0.5, where repulsive and attractive interactions are balanced [74].

Figure 5.

Dimensions of different FG nup chains. A: Classification of different FG nups based on their compactness as a function of the hydrophobic-to-charged amino acid content ratio. Reproduced from [101], permission pending. B: Stokes radii of various FG nups and FG nup segments calculated by one-bead-per-amino-acid model (in Kirkwood approximation), compared with experimental data; see text for details. Reproduced from [62], permission pending. C: Experimental FG nups dimensions analyzed using mean field Flory type polymer model. Increasing the cohesiveness makes the coils more compact and decreases the scaling exponent (see text). Dots: experimental data (normalized). Solid black, red, green and blue lines are the theoretical model predictions for chains of different length appropriate for the corresponding FG nups. The cohesiveness is proportional to the hydrophobic content of the chains. Reproduced from [56], permission pending.

The nature of the individual FG nup chains has been further probed by density functional and molecular dynamics models that more explicitly take into account the specific amino-acid composition of the different FG nups. Ghavami et al. [62,147] described the FG nups as chains of beads with one bead per amino acid, with explicit parametrization for electrostatic and hydrophobic interactions as well as bond stretching, bond bending and bond torsion potentials based on Ramachandran data of the coiled regions of protein structures. The parameters were selected to match experimental hydrophobicity scales for the different amino acids and scaled to match the dimensions of a low-charge and high-charged FG nup segment. These works calculated the Stokes radii using hydrodynamic theory of interacting beads based on Kirkwood theory [148,149]. The resulting model reproduced the experimentally obtained Stokes radii of a wide range of FG nups and FG nup segments [40,101] with a maximal error of 20%, as shown in Figure 5B.

Another experimental assessment of FG Nup dimensions was performed by SAXS and FRET experiments that directly probe the equilibrium conformations and the dimensions of the FG nups [124,150]. While smFRET provides distance information between two distinct points in an IDP chain which provides a measurement of R_E, the radius of gyration R_G can be measured by SAXS and is an average manifestation of all interatomic distances and thus provides a measurement that is complementary to smFRET [124,151,152]. Due this weighting, however, R_G is often dominated by inter-residue distance at shorter length scales (<40 residues [124]), and can thus be less sensitive towards collapse and scaling behaviour of FG nups specifically and IDPs in general. Furthermore, interpretation and comparison of FRET and SAXS experiment commonly relies on homopolymer theory, and it still remains to be established to what extent this can be used also for heteropolymers such as FG nups [124]. Atomistic models have been a powerful tool in analyzing FRET and SAXS experiments, despite some of their deficiencies mentioned above. The solvation problem of IDPs in traditional force fields has been partially tackled by using force fields based on Kirkwood-Buff solution theory. This approach has been successful in better matching experimental observations from FRET, SAXS and NMR [135]. This approach has also been successful in recapitulating small, yet experimentally (smFRET) resolvable changes in FG nup collapse upon minor modifications such as removal of ~2 proline residues [153]. Another powerful approach involves constraining MD simulation ensembles with experimental observables such as distance restraints from FRET and R_G from SAXS [124]. More experimental and theoretical work is required for a consistent interpretation of smFRET and SAXS data [124,154]

Due to the technical challenges of both methods, only limited amount of experimental data are currently available for SAXS and smFRET, but overall the data obtained so far is consistent with the above mentioned hydrodynamic radius measurements and their interpretations in terms of polymer concepts. For different human and yeast FG nups, smFRET and SAXS yielded scaling exponent ν 0.45 and 0.61, ranging between collapsed and relaxed coil configurations [124,150]. For instance, human Nup153 FG fragments may appear more relaxed, whereas human Nup98 is more collapsed. Overall, these results are qualitatively similar to several other assays that aimed to detect cohesiveness/propensity of self-interaction in FG nups [41,101]. The more collapsed nature of human Nup98 is consistent with the observation that Nup98 from different species can undergo a phase separation into hydrogels that recapitulate the transport selectivity of the pore [104]. Atomistic simulations of artificial FG nup-like constructs have also observed the expected scaling, although the results depended on the choice of water model [134].

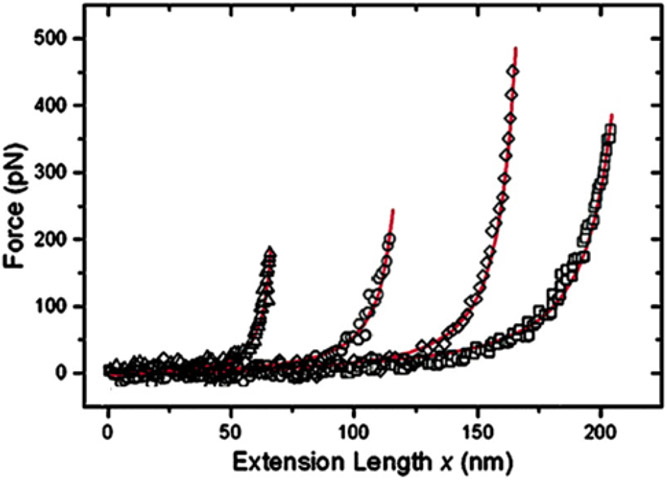
Finally, the descriptions of FG nups based on the concepts of polymer physics have been validated in measurements of their resistance against mechanical extension using atomic force microscopy (AFM), as shown in Figure 6. In these experiments [73], a human FG nup (Nup153) was grafted at one end to a rigid surface. By pulling on the chain at different positions along its contour length with an AFM tip, the force-versus-extension was found to show classical worm-like chain behavior [155]. These experiments yielded a mean persistence length of 0.39 ± 0.14 nm for this FG nup, comparable to the size of an individual amino acid (~0.4 nm). At length scales beyond the persistence length, angular correlations become negligible and the polymer behaves as a flexible chain.

Figure 6.

The nanomechanical behavior of FG nups is consistent with that of polymer models. Surface grafted FG nups were pulled by AFM at different locations. The force-extension curves(symbols) are well described by worm-like chain fits (red lines). Adapted from [73], permission pending.

In summary, thanks to the combination of multiple experimental methods with multi-scale computational approaches, the structure and the dynamics of FG nups have been characterized at the single chain level. In many aspects, FG nups behave like long, flexible polymer molecules with some degree of cohesiveness. Much of their nano-mechanical behavior on the relevant time- and length-scales can therefore be described by simple polymer physics and expressed in mathematical models of differing degrees of complexity. This insight provides a basis for understanding the collective behavior of FG nups in more condensed phases such as in the NPC, as described in the following sections.

3.3. Collective effects in assemblies of FG nups

3.3.1. Bulk phases and phase transitions of FG nups

Within the NPC, approximately 200 FG nups of a typical molecular weight ~100 kDa, and containing ~150-800 amino acids each in their intrinsically disordered regions, are end-grafted to the walls of the central channel that bears an inner diameter of ~40 nm and a length of several tens of nm ([5] and references therein). Hence, the concentration of FG nups inside the NPC is of the order of mM, or ~100 mg/mL [62] with an approximate volume packing fraction of ~10%. Considering that a large fraction of the NPC passageway is occupied by transport factors and/or cargo in transit, the local FG nup and transport proteins density may even be considerably higher [7,57,62,83,104,158].

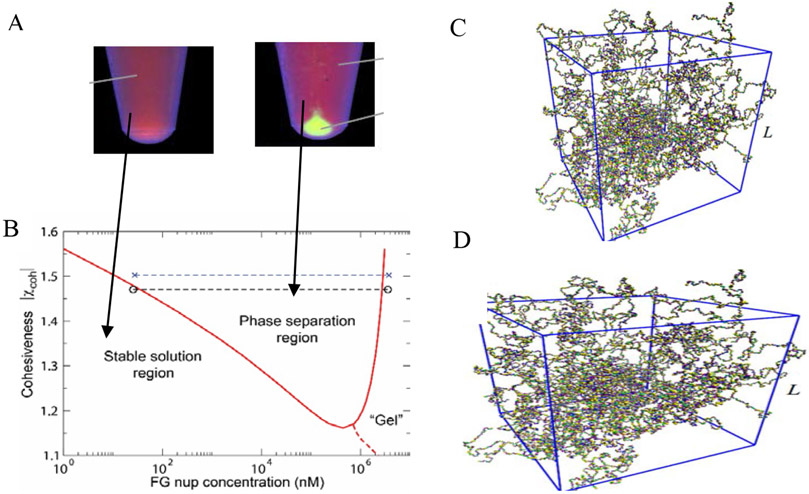
At such high concentrations, the interactions between individual FG nup chains come to play, potentially leading to collective effects. Given their intrinsic cohesiveness, there is a propensity for some FG nups (such as Nup98 or Nup100/116) to form dense multi-molecular assemblies or aggregates (Figure 7A). In early works, FG nup aggregation produced irreversible dense condensates that were reminiscent of polymer “gels”, but the experimental conditions were far from physiological [97,109]. More recent work has shown that dense non-surface grafted FG nups can also self-aggregate under more physiological conditions [104]. The mechanism of initial formation of these droplet-like aggregates from a dilute solution of FG nups resembles a phase separation of self-associating polymers where a dense polymer phase co-exists with a dilute solution of chains as shown in Figure 7A,B [159,160].

Figure 7.

Phase separation and gelation in solutions of FG nups. A: Dense aggregates (yellow “droplet”) are formed by cohesive FG nups at sufficiently high concentrations. Adapted from [98], permission pending. B: Phase diagram of an FG nup solution obtained using Flory-Huggins type theory of Eq. (3). The red line indicates the theoretically predicted boundary of the phase separation region. Dashed line: schematic boundary of the formation of the percolating “gel”. Symbols: experimentally observed densities of the dilute and the dense phase. Reproduced from [156], permission pending. C: Gelation in FG nup solutions studied by a molecular dynamics model with one bead per amino acid. D: Critical concentration for gel formation ccrit as a function of the charge C, hydrophobicity H, and FG nup length N, as follows from applying percolation theory to the simulation results. The results show that hydrophobic interactions are the main driving force for gel formation in FG-nup solutions, reflected in the increase of the critical concentration for gel formation increases with the charge-to-hydrophobicity ratio. Adapted from [157], permission pending.

However, all FG nup aggregates have a high tendency to age into solid-like states, commonly enriched in amyloid fiber type structures, a process that in other phase separation proteins has been referred to as molecular aging [161-163]. A recent microfluidic platform was used to trigger phase separation of an FG nup quickly and to optically interrogate the properties of emerging droplets, which clearly showed that freshly formed FG nup droplets show liquid properties, such as coalescence and deformability [164]. The microfluidic device also enabled to test for permeability barrier properties of the liquid FG nup assemblies (see Section3.4).

Two main factors control the behavior of the solutions of interacting polymer chains: the entropy of the polymer molecules in space (and the corresponding solvent entropy) and the interactions between the chains. Interestingly, the intra-chain configurational entropy, which is so important in determining the properties of individual polymer chains, is not fundamental for polymer solutions [127]. In the classical mean field model, known as the Flory-Huggins theory, the free energy (per unit volume) of a polymer solution is

$$\frac{F}{k_{B}T}=\frac{\psi }{N}ln(\psi )+(1-\psi )ln(1-\psi )+\frac{1}{2}{\chi }_c{\psi }^2,$$ (3)

where N is the number of monomers in the chain and ψ = nν₀ is the volume fraction occupied by the polymers, with ν₀ the volume of a monomer and n the average monomer density as before [127]. Although the Flory-Huggins free energy is commonly derived on a lattice, it has a general applicability due its simple physical interpretation. The first term in equation (3) describes the translational entropy of the chains in space. The second term describes the reduction in the entropy of the polymer chain configuration due to steric repulsion (excluded volume) between them; it can be also interpreted as the entropy of the surrounding solvent [121]. The last term in this equation describes the attractive/cohesive interactions between the monomers of the polymers, similar to the expression for an individual polymer in Equation (2). This cohesiveness parameter χ_c subsumes all the intra- and inter-chain molecular interactions on the average level and is related to the second virial coefficient of the monomer-monomer interaction [127].

For sufficiently strong cohesiveness, χ_c > 1 + 1/√N, the system undergoes a phase separation, resulting in the formation of a dense phase in equilibrium with a dilute solution [56,127]. This minimal-complexity model incorporates only the key equilibrium properties of the FG nup molecules and their interactions, yet is in remarkable agreement with the experimental observations, as illustrated in Figure 7B. Note that the formation of the percolating “gel”-like network of FG nups (sometimes known as a sol-gel transition) is not necessarily accompanied by a phase separation, and can theoretically proceed in a continuous manner [165-168].

The insights of the minimal models are consistent with more detailed simulations that take into account the amino acid sequence of the FG nups as described in Section 3.2 [59,62,63,169,170]. Using such simulations, the sol–gel transition was studied by considering the propensity of FG nups to form (reversibly) cross-linked networks, defined by the formation of a percolating network of residues of different FG nups approaching each other to below a critical distance [157], as shown in Figure 7C. The computed critical concentrations for gel formation were found to increase with charge content and decrease with hydrophobic amino acid content and chain length, consistent with the predictions of the mean field theories. Notably, the computed critical concentrations are lower than the typical FG nup concentrations found for yeast NPCs [62] and in selective biomimetic nanopores [25], supporting the hypothesis that the FG nup gel-like state may form in the confinement of the NPC transport channel. This observation comes with the caveat that, unlike the bulk simulations of [157], the NPC contains multiple different FG nups which are anchored to the pore scaffold. Furthermore, the current theoretical and computational model do not include amyloid-promoting interactions such as hydrogen bonds that might result in more complex 3D structures [104,161,162].

Finally, these collective FG nup morphologies are sensitive to interactions with the cellular milieu, and are likely to be modified in the presence of the transport proteins and other proteins in the dense environment of the cell, as discussed in the next section.

3.3.2. Assemblies of FG nups grafted to planar surfaces

To study the collective behavior of FG nups under conditions that more closely mimic their assembly in the NPC, various model systems have been developed in which FG nups were grafted to planar surfaces at the grafting densities resembling the NPC transport channel [57,99,108,113,130,171-174]. This allows more systematic study of FG nup properties whilst preserving a key physical attribute of the NPC, the grafted nature of the FG nups at physiological densities.

In these experiments, FG nup molecules are typically attached to solid surfaces using diverse experimental techniques: cysteine-tagged FG nup constructs grafted to gold surfaces [99,173,174], histidine-tagged FG nup constructs to a supported lipid bilayer containing functionalized lipids [130], or directly to commercial PEG-functionalized silica substrates via divalent metal ions [171]. Collective morphologies and conformational states of the FG nups in the layer are reflected in the layer height that can be measured through a number of surface-science based methods. These include indentation by atomic force microscopy (AFM), quartz-crystal microbalance with dissipation monitoring (QCM-D), spectroscopic ellipsometry (SE), and surface plasmon resonance [57,99,108,113,130,171-174].

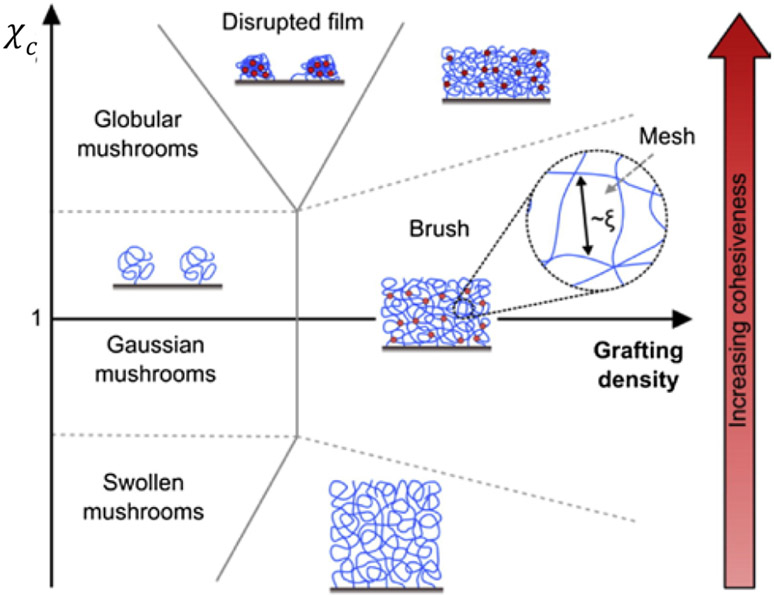
Surface grafted polymer layers have been studied extensively and are well understood in terms of concepts and key variables determining the collective polymer behavior [175-177]. These insights also translate to grafted layers of intrinsically disordered polypeptides [178]. A wide range of collective morphologies may be observed in surface grafted polymer layers, depending on the grafting distance and on the cohesiveness of the polymers, as illustrated in Figure 8. In the absence of polymer-surface interactions, a single surface-grafted polymer chain adopts a coil-like “mushroom” conformation, similar to its shape in solution, due to the thermal motions of the chain monomers. In sufficiently dense multi-polymer grafted layers, where the next-neighbor grafting distance is closer than the natural dimension of an individual mushroom, the layer adopts a structure known as the polymer “brush”. Here, each chain becomes more stretched in the perpendicular direction than in the lateral direction, being stabilized by the steric repulsion that results from the thermal motion of the adjacent chains, known as “entropic stabilization” [175]. Similar to individual polymer coils in solution, mushroom size and brush height can be modulated by inter- and intra-chain cohesion and solvent properties that favor more compact morphologies [56,179,180]. Nevertheless, despite significant stretching, each chain in a polymer brush is still sufficiently coiled, and the resulting diffuse structure typically contains a large amount of free water. Accordingly, the average brush height as measured from the grafting surface is typically much shorter than the fully extended contour length of the polymer, and can be controlled by varying the grafting density [175].

Figure 8.

Schematic phase diagram, illustrating different types of behaviors of layers of end-grafted polymers as a function of the interaction parameter χ_c and the grafting density. Adapted from [108], permission pending.

Basic insight into the collective morphologies of surface grafted FG nups can be obtained within the same conceptual framework that describes the properties of individual FG nups in solution. In the simplest mean field model, also known as the Alexander-de Gennes model[179], for a layer of polymers with a length of N monomers, each grafted at a distance a from each other, the free energy per unit area is given by an expression that parallels the free energy of a single chain of Equation (2):

$$\frac{F}{k_{B}T}=\frac{h^2\sigma }{2N}+g(n)h,$$

where h is the layer height, $\sigma =\frac{1}{a^2}$ is the surface grafting density (number of polymers per unit area) and g(n) is the interaction part of free energy density of the solution of monomers within the layer described in Section 3.3.1 [56,181]. The monomer density inside the layer is n = σ/h, and the equilibrium height is found via minimization of the free energy over h. This oversimplified model neglects a number of potentially important features, such as non-uniform monomer density inside the layer and the effects of the FG nup sequence heterogeneity. Nevertheless, the resulting predictions are in agreement with more detailed models based on self-consisted field approximation and other methods [181,182].

Increase in the intra- and inter-chain cohesiveness causes a decrease in the layer height. Analogous to the coil-globule transition of single polymer coils in solution, this compaction is accompanied by a qualitative change in the scaling of the layer height with the grafting distance a [56,176,183]. In the absence of cohesiveness, for a “pure” sterically stabilized brush, the layer height scales as h ~ a^−2/3 [175]. As the cohesiveness increases, the scaling exponent increases to h ~ a⁻² for a compact layer [56]. This is analogous to the transition from the Flory exponent ν = 3/5 for relaxed coils to ν = 1/3 for compact globules of single chains described in the previous section. In the polymer physics parlance, this transition is analogous to the change from a “good” to a “bad” solvent.

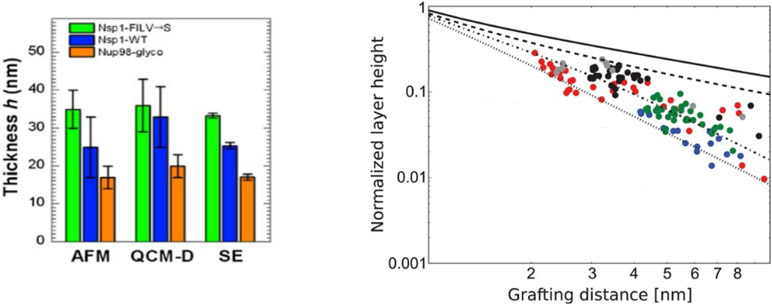
The experimental results agree well with this theoretical picture, across many experimental platforms and different FG nup types, as summarized in Figure 9. Similar good agreement was obtained using other coarse- [57] and finer-grained [62] molecular models. Taken together, these experimental results, combined with theoretical and computational modeling show that surface layers of grafted FG nups are well described as moderately cohesive flexible polymeric brushes, consistent with their behavior in bulk solutions [56,57,173]. Nevertheless, FG nup sequence detail may play an important role. It has been shown that many FG nups possess “di-block polymer” nature, where the cohesive FG repeat rich domains are segregated from FG poor, more charged domains, which may play a role in their collective conformations [53,111]. Furthermore, atomistic modeling indicates that FG nup in brushes may braid into multi-chain bundles that expose FG repeats on their surface [55,133], which may be related to the experimentally inferred amyloid-like structures within FG nup assemblies [104,161]. These atomistic and one-bead-per-amino-acid simulations provide the molecular underpinning for the average mean field parameters such as the chain cohesiveness χ_c that cross-verifies their estimates based on the single molecule and brush measurements.

Figure 9.

Effects of chain cohesiveness and density on the morphology of FG nup surface layers. Left: FG nup layer heights measured for three different FG nups (orange is the most cohesive one (nup98), blue is the less cohesive one (Nsp1) and green is the even less cohesive mutant of blue. The measured height is consistent between atomic force microscopy (AFM), quartz-crystal microbalance with dissipation monitoring (QCM-D), and spectroscopic ellipsometry (SE). Reproduced from [108], permission pending. Right: Increasing the grafting distance decreases the layer height, in accord with theoretical expectations. Dots are experimental data for different (human) FG nups measured using surface plasmon resonance (SPR). All measured FG nups layers behave as cohesive polymer brushes and lie between the theoretical predictions for the pure repulsive brush (solid line) and the fully compact brush (dotted line). Dots show experimental data. Different colors correspond to different FG nup types. Reproduced from [173], permission pending.

3.3.3. FG nups in NPC mimicking synthetic nanopores

To further approximate the spatial arrangement of FG nups in the confined geometry of the NPC, several studies have employed FG nup layers grafted into artificial nanopores of dimensions similar to those of the NPC channel (Figure 10). These include nanochannels in polycarbonate membranes [23] and solid state nanopores [24-26,28]. NPC mimics allow quantitative investigation of FG nup morphology and the translocation of transport proteins in a minimalistic, well-controlled system focusing on specific FG nups. Hence, structural and functional measurements on these systems are more readily interpreted in terms of FG nup properties compared to measurements in biological setting. In particular, these mimics serve as testbeds for the verification and calibration of the computational models [25,54,59-63,110,111,184,185].

Figure 10.

Nanopore mimics of the NPC. A: (Left) Polycarbonate membrane perforated by ~30 nm channels, coated on one face with a ~15 nm gold layer. (Right) FG nups are grafted to the gold layer by s ingle C-terminal cysteines. PEG is used to block unspecific binding to exposed gold. Reproduced from [23], permission pending. B: Schematics of a nanopore drilled in a silicon nitride (SiN) membrane by a focused electron beam. FG nups are grafted to the silicon nitride by a terminal thiol. Reproduced from [25], permission pending. C: DNA origami pore scaffold containing 48 single-stranded DNA handles, allowing specific attachment of FG nups that are conjugated with the matching single-stranded DNA sequence. Reproduced from [28], permission pending.

A downside of the earlier NPC mimics [23,25,26] was the lack of control over the grafting positions and grafting densities for FG nups in the nanopores. To address this problem, more recent approaches use DNA origami pore scaffolds that expose precise numbers of single-stranded DNA handles on the scaffold structure. Purified FG nups are chemically conjugated with single-stranded DNA linkers that match the sequence of the handles, and thus grafted to the DNA origami scaffold at the handle positions [24,28]. However, for these DNA-origami based mimics, NPC-like transport functionality has yet to be demonstrated, which may be related to the substantial negative charge of the DNA, which is absent in the actual NPC scaffold. Another approach focusing on de novo reconstitution of NPCs uses self-assembly of NPC pore membrane proteins into ~20 nm-diameter nanopores in lipid bilayers [187].

The rudimentary NPC-like affinity-based selectivity is also observed in completely synthetic nanopores that use synthetic polymers [27], and provide a link to a wider field of design of polymer functionalized nanochannels for various nanotechnology applications such as protein sorting, DNA sequencing and “smart” materials [146,188-199]. Such artificial nanopores, although not the direct focus of this review, can also serve as experimental venues for testing the conceptual models of NPC transport.

We return to the transport functionality of these NPC mimics in Section 4. In this section, we focus on the morphology of the FG nups in the nanopore geometry.

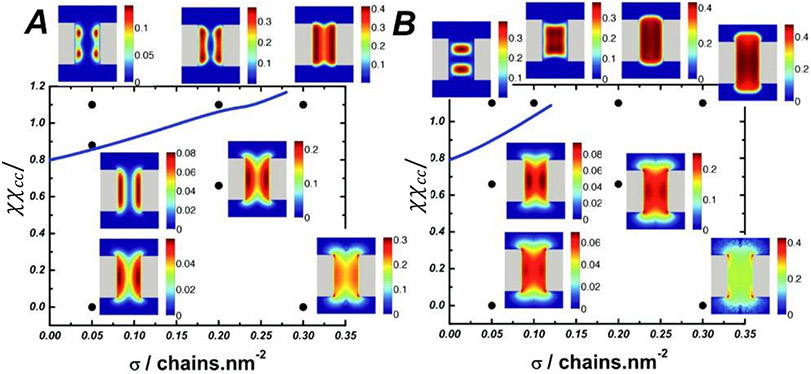
From a general perspective, the same factors that affect the morphology of polymer assemblies grafted to flat surfaces also determine their behavior in cylindrical channels, with an additional control parameter, the channel radius, that adds to the richness of the phase behavior [186,200-202]. The different regimes and factors controlling the transitions between them are summarized in Figure 11. In brief, paralleling the behavior of planar assemblies, the intra- and inter-chain cohesiveness controls the transition from diffuse/extended to more condensed/collapsed states. However, in the channel geometry the grafted layer can condense either towards the grafting walls or towards the center of the channel, depending on the relative dimensions of the channel and of the polymers [45,184,186,200].

Figure 11.

Phase diagram of possible morphologies of cohesive polymers grafted in nanochannels as a function of the grafting density σ and the chain cohesiveness χ_c. For short chains (left panel), increasing cohesiveness causes the chains to compact towards the walls, similar to the planar surfaces. Longer cohesive chains (right panel) can collapse towards the center instead. Adapted from [186], permission pending.

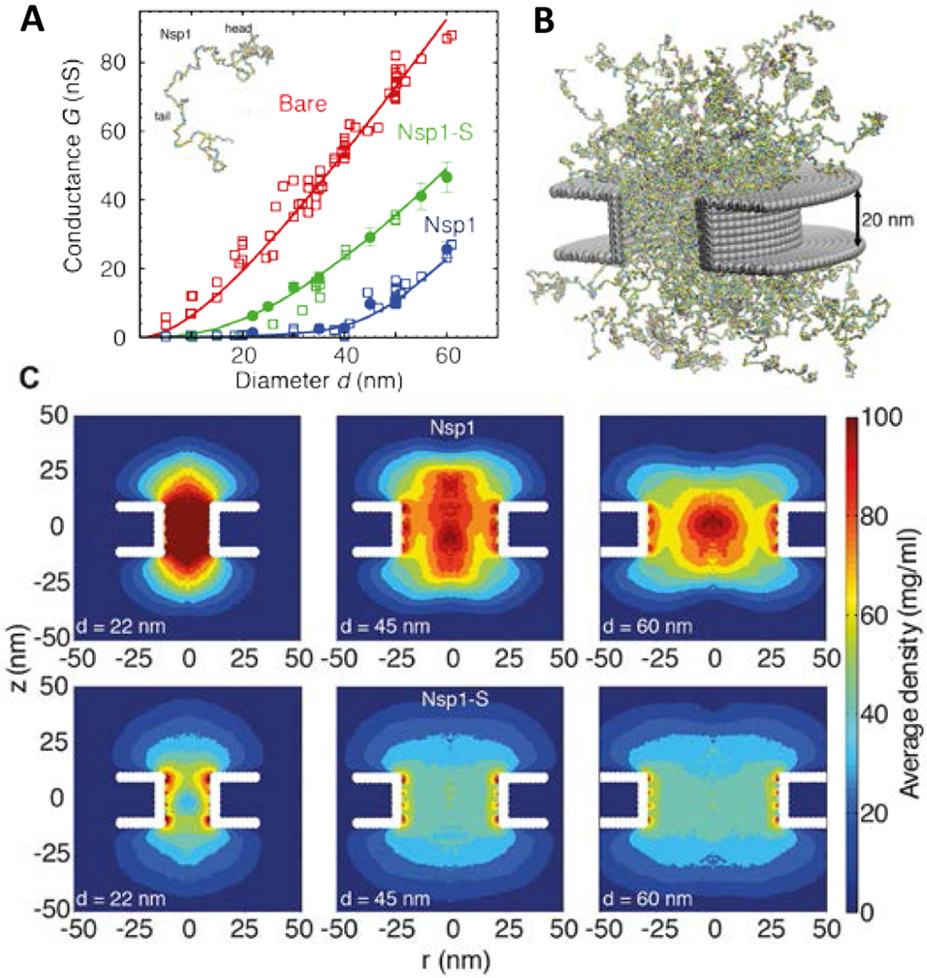
There is good agreement between, on one hand, detailed molecular modeling that incorporates the full amino acid sequence of the FG nups, and, on the other hand, the insights from the simple polymer models, and both have been used to interpret experimental data in nanopores coated with FG nups of different degree of cohesiveness. As illustrated in Figure 12 [25], molecular modelling can capture the experimental ionic conductances showing that the FG nup chains partially block the ionic flux through the pore with the flux being related to the FG nup density distribution using certain assumptions about the dependence of the local ionic conductivity on the local molecular density (see references in [25]). Consistent with the theoretical expectations, the more cohesive FG nup Nsp1 shows higher density along the central axis of the channel (see Figure 12). In contrast, simulations of the less cohesive Nsp1-S mutant, with the hydrophobic Phenylalanines being mutated to hydrophilic Serines, predict lower densities and a more uniform distribution within the pore. By increasing the channel radius, the density of the FG nup cloud in the pore decreases, opening conduction pathways, accompanied by the increase in the ionic conductivity, as observed experimentally. Whether these low-density pathways are located next to the channel walls or along the central axis may depend on the channel radius and the FG nup type [25,26]. Notably, this behavior is largely consistent with the general theoretical expectations of Figure 11, based on homopolymer models [45,53,60,114,184,186,203].

Figure 12.

FG nups grafted in a nanopore. (A) Ionic conductance as a function of nanopore diameter for the bare pore (red), for a pore covered with the yeast FG nup Nsp1 (blue), and for a pore covered with the less cohesive mutant Nsp1-S (green). See text for discussion. Open symbols: experimental data. Closed symbols and lines: theoretical predictions. (B) Snapshot of simulations of the Nsp1 pore. (C) Time-averaged protein density distributions in Nsp1 and Nsp1-S pores; note that qualitatively similar dependencies of the polymer morphologies on the parameters are present in Figure 11. Adapted from [25], permission pending.

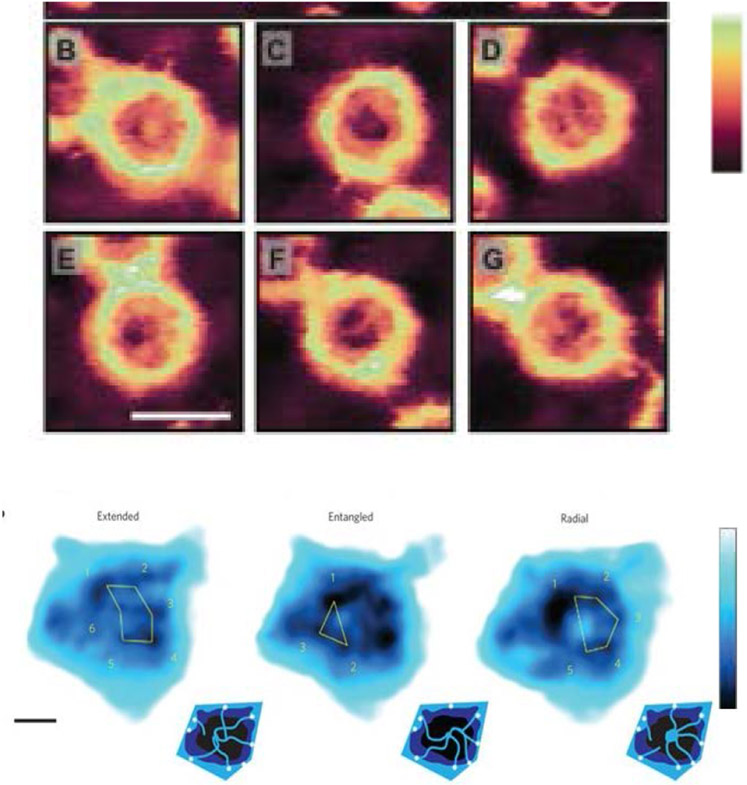
The different spatially condensed states (or phases) shown in Figure 11 and Figure 12, raise a possibility of bi-stable behavior of the polymer layer, switching between “open” and “closed” states in some parameter range. [58,184] (Figure 13, top). These predictions may be related to the collective dynamic rearrangements of FG nups in nanopores observed by fast AFM [28,204], with FG nups alternating from one clumped/condensed configuration to the other (Figure 13, bottom), and possibly switching between more open and more closed configurations. (The technique comes with the caveat that the AFM tip might have an effect on the observed behavior.) Further Brownian dynamics simulations suggest that the FG nup assembly might alternate between these open and closing configurations during cargo translocation [170].

Figure 13.

Collective re-arrangements of polymers in the pore. Top: as shown by Monte Carlo simulations of polymers in a cylinder. Bottom: sequential AFM images of FG nups in DNA-origami ring scaffolds, recorded at 1.6 sec/frame. Reproduced from [58] and [28], permission pending.

In summary, NPC-mimicking nanopores have provided fundamental insights into the potential collective conformations of the FG nups in nano-confinement geometries resembling the NPC. They also enabled calibration and testing of the computational models of FG nups in physiologically relevant geometries. Overall, experimental and computational approaches are converging in our understanding of the biophysics of the FG nups in pore geometries. Notably, many of the features of the FG nup distribution in the nanopores are recapitulated both in simulations that take into account the full amino acid sequences, and in ultra-coarse grained, homopolymer models with averaged interaction parameters. Nevertheless, the full experimental characterization and theoretical understanding of the structure of the FG assemblies still remains for the future. In Sections 3.4.5 and 4.1.4, we discuss how this understanding extends to the collective behavior of FG nup morphologies in the presence of transport proteins, as well as to their dynamics during transport.

3.4. Interactions of FG nups with transport proteins

Specific, transport-protein driven transport through the NPC crucially relies on the binding of the transport proteins to the FG nups in order to at least partially offset the free energy costs of penetrating the FG nup assembly in the NPC [5,6]. Accordingly, this interaction is a consensus component of all models of NPC function. The interactions of the transport proteins with the FG nups have been intensively studied during the past two decades with the goal of identifying the main physical variables and molecular features that facilitate penetration of transport proteins into FG nup assembles [56,57,99,106,119,130,150,152,173,174,205-211]. Yet, the quantitative characterization of such interactions is challenging. The main obstacles are chain flexibility, multivalency of the interactions, FG nup sequence heterogeneity, and collective effects of the environment that complicate the relations between the macroscopic measurements and microscopic interactions.

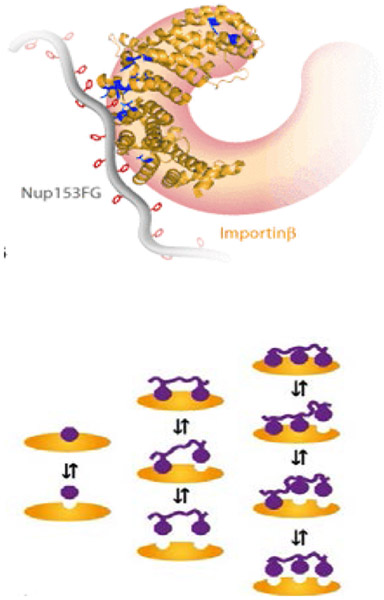
Moreover, the knowledge of the exact molecular nature of the interactions between the transport proteins and the FG nups is still incomplete. Previously, the hydrophobic interaction between the hydrophobic Phenylalanines (F’s) and the hydrophobic grooves on the transport proteins was considered to be the primary driver of the transport protein binding to the FG nups. However, the actual number of the binding sites on the transport proteins in general is not fully known, and structural studies have been able to confirm only a few definite binding sites [106,107,205] out of the up to 14 potential binding sites on the larger transport proteins (such as Importin β) that were suggested by computational studies [210-212]. Other computational studies have highlighted the potential role of electrostatic interactions in the transport protein/FG-nup binding [63,105]. This goes in line with recent experimental work which established that the permeability of the NPC with respect to various cargoes is determined not only by the hydrophobic binding sites on their surface but also by charged, cation-π, and π − π forming residues [96,213,214].

3.4.1. Quantification of interactions between FG nups and transport proteins: thermodynamics

Measurements of the affinity of interaction between transport proteins and FG nups have been performed on FG constructs ranging from the “elementary interaction unit” (one FG ‘patch”) to the full-length proteins using a range of transport proteins.

The interaction between a transport protein (NTF2), which contains only two known FG binding sites, and a polypeptide construct incorporating a single FG “patch” been measured in solution by NMR and isothermal calorimetry and yielded a dissociation constant of K_d ≃ 3 − 4 mM, which corresponds to an effective binding energy of approximately E = 5 k_BT assuming mostly monovalent binding with K_d = 1M · e^−E/k_BT [209]. Similar values were found for various native and artificial FG nup constructs and transport proteins in solution, with dissociation constants in the range of hundreds of μM to several mM, depending on the number of FG motifs in the sequence and the distance between them [103,119,209]. Nevertheless, binding of some FG nups to transport proteins can be significantly stronger.

By contrast, the dissociation constants of transport proteins (Importin-β) and surface-grafted full-length FG nup segments (containing multiple FG motifs) were measured using surface plasmon resonance (SPR), and found to be in the μM range in sparse grafting “mushroom” regime [173], where one might assume 1:1 stoichiometry between FG nups and transport proteins (though not between FG motifs and transport proteins, which can compound the interpretation). In the “brush” regime, the dissociation constants were found to be in the range of hundreds of nM to several μM (depending on the FG nup and transport protein type) [8,57,130,173,174]. However, the interpretation of the “brush” results is complicated by the possible non 1:1 stoichoimetries, by high density effects and by spatial heterogeneity: hence not surprisingly, the binding curves do not obey a Langmuir shape for simple one-to-one binding, as discussed below. Other studies using micro-bead assays found, in some cases, dissociation constants in the nanomolar range, although it was realized that these nanomolar affinities are probably not physiologically relevant [206,208,215].

Some of these discrepancies might be attributed to the differences in experimental conditions, e.g. Importin-β with multiple binding sites vs smaller NTF2 with smaller number of binding sites, or the different FG nup segments used. However, more generally, the interpretation of the effective dissociation constants in terms of local interaction strengths between the FG nups and NTRs remains elusive due to several complicating factors.

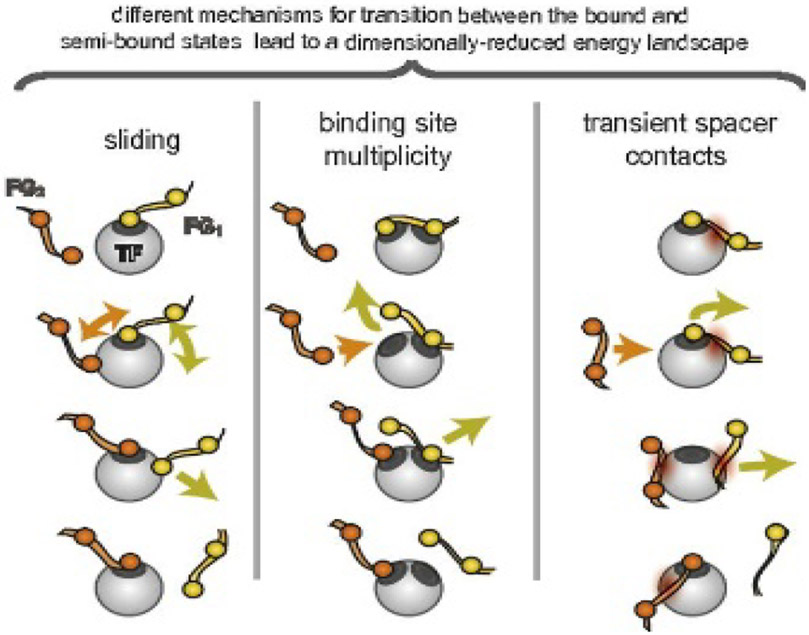
The first factor is the multivalency (commonly known as “avidity”) of the interactions between transport proteins and FG nups: while the affinity between a transport protein and a single FG “patch” may be low, much stronger binding may be observed when multiple FG repeats are accessible on the same chain or – in FG nup assemblies – on multiple chains.

Some of the effects of avidity/multi-valency can be understood within a simple toy model (see also [145]). Consider a polymer with M cohesive “patches” and a particle with N binding sites within a box of volume V. Assuming the polymer is “bound” to the particle if it is located within a certain volume ν_p ≪ V around the particle and at least one of the “patches” is bound to a binding site on the particle, the bound probability is given by

$$P_b=\frac{v_p∕V{\sum }_{k=1}^N\left(\begin{array}{c}\hfill N\hfill \\ \hfill k\hfill \end{array}\right)\left(\begin{array}{c}\hfill M\hfill \\ \hfill k\hfill \end{array}\right)e^{-ϵk}}{1+v_p∕V{\sum }_{k=1}^N\left(\begin{array}{c}\hfill N\hfill \\ \hfill k\hfill \end{array}\right)\left(\begin{array}{c}\hfill M\hfill \\ \hfill k\hfill \end{array}\right)e^{-ϵk}},$$

where ϵ < 0 is the binding energy between a “patch” and a binding site measured in units of k_BT. For the sake of the example, we have neglected the entropic contributions of the inter-patch likers and the associated correlations between different patches. These correlations can substantially modify the results via the mechanism known as local density enhancement [209,217]. The degree of this enhancement depend in part on the entropy of the flexible inter-FG spacers, which is difficult to compute [114,209,217].

The dissociation constant is given by [218]

$$K_D=\frac{(1-P_b)\cdot \frac{1.}{V}1∕V}{P_b∕V}\simeq \frac{1}{v_p}{\left({\sum }_{n=1}^N\left(\begin{array}{c}\hfill N\hfill \\ \hfill n\hfill \end{array}\right)\left(\begin{array}{c}\hfill M\hfill \\ \hfill n\hfill \end{array}\right)e^{-ϵn}\right)}^{-1}$$ (4)

For N = 1, M = 1 this expression reduces to the familiar formula for the dissociation constant of simple monovalent binding $K_D\simeq \frac{1}{v_p}{e}^{ϵ}$ so that affinity is high (K_D small) for strong binding (strongly negative ϵ < 0) [219]. For particles with only one binding site and multi-patch polymers, N = 1, $K_D\simeq v_0^{-1}{M}^{-1}{e}^{ϵ}$; as expected, the prefactor M⁻¹ reflects the increase in the association rate due to the multiple available binding sites on the polymer.

Second, in multi-chain settings, multivalency makes the apparent binding affinity of the transport proteins to FG nup assemblies dependent on the spatial density of the FG repeats [173,220]. From the analysis of assays using surface grafted FG nup layers, it emerged that the estimated dissociation constants strongly depend on the grafting density of the FG nups on the surface [173]. The interpretation of the experiments is further complicated by the fact that the binding curves can substantially differ from classical one-to-one (Langmuir) binding models with a single value of binding affinity [56,57,130,173,182,221]. This context-dependence also manifests itself in the sensitivity of the measured affinities to the presence of soluble competitors, such as other transport proteins or macromolecules [174]. For instance, the presence of cell lysate was shown to weaken the observed equilibrium binding affinity by orders of magnitude [103,206,222].

The context-dependent nature of the transport protein affinity to the FG nups can be illustrated in another toy model as follows. Consider a transport protein as a particle with N binding “patches”, which resides in a milieu of polymeric chains with M binding sites each. The polymer concentration is defined as C/M, so that the average concentration of the binding sites around the particle is C (measured in units of $v_0^{-1}$, where ν₀ is a typical molecular volume). For the sake of the example, we neglect correlations between the binding sites that lie on the same chain, appropriate in the high-density regime because the particle is typically bound to many chains simultaneously.

The fraction of the particles bound at least at one site is $\frac{{\sum }_{n=1}^N\left(\begin{array}{c}\hfill N\hfill \\ \hfill n\hfill \end{array}\right)C^n{e}^{-ϵn}}{Z}=(Z-1)∕Z$ [217,223] where ϵ < 0 is the binding energy of each individual contact measured in units of k_BT, and $Z={\sum }_{n=0}^N\left(\begin{array}{c}\hfill N\hfill \\ \hfill n\hfill \end{array}\right)C^n{e}^{-ϵn}=(1+C{e}^{-ϵ}{)}^N$ is the partition function. Accordingly, the fraction of the particles that are not bound to any polymer is 1/Z. Thus, an effective dissociation constant can be defined as [219]

$$K_D=v_0^{-1}\frac{C∕M\cdot (1∕Z)}{({\sum }_{n=1}^N\left(\begin{array}{c}\hfill N\hfill \\ \hfill n\hfill \end{array}\right)C^n{e}^{-ϵn})∕Z}=v_0^{-1}{\left(\frac{M}{C}(Z-1)\right)}^{-1}=v_0^{-1}\frac{1}{M}\frac{C}{(1+C{e}^{-ϵ}{)}^N-1}.$$

At a high concentration of the polymers, when Ce^−ϵ ≫ 1, the effective dissociation constant is K_D ≃ M⁻¹e^ϵC(Ce^−ϵ)^−N. As a consequence, the effective affinity is strongly density dependent, and particles can experience much higher effective affinity in high-density FG nup assemblies.

To summarize, in general care should be exercised when inferring microscopic interaction parameters from macroscopic measurements of the binding affinities (which are significantly context-dependent) and translating from in vitro measurements to in vivo interactions in crowded cell environments. The dense assemblies of transport proteins and FG nups are further discussed in Sections 3.4.3-3.4.4. The relation between the FG nup-transport protein equilibrium interactions, kinetics and transport is described in Section 3.4.2 and Section 4.

3.4.2. Kinetics of the FG nup- transport protein interaction

One of the big questions about NPC operation is the contrast between its strict thermodynamic selectivity and the rapidity of transport. In particular, given the effective binding affinities of 1 μM and a typical protein association rate of k_on ~ 10⁵ − 10⁶ M⁻¹ s⁻¹, the expected dissociation rate is k_off = k_onK_d ~ 0.1 − 1 s⁻¹, which is incompatible with the millisecond transport times observed in the NPC.

This paradox might be partially explained by the high observed association rates (k_on) of transport proteins and FG nups [103,119,224] that arise from the combination of the multivalent interactions and the high conformational flexibility of the FG nups. Measured for the binding of several pairs of FG nups and transport proteins using stopped flow spectroscopy, the resulting association rates (k_on) were found as high as 10⁹ M⁻¹ s⁻¹, close to the theoretically maximal diffusion limit [119]. In particular, it was found that the FRET efficiency between dyes an FG nup does not change appreciably upon transport protein binding [119]. This indicates that FG nups bind transport proteins not in one specific configuration, but across a wide range of conformational states, with rapid conformational exchange between different states – a feature also confirmed by NMR [103,119,209]. Similar concepts have been invoked in the analysis of a classical “fuzzy complex” observed for other multivalent protein interactions [225]. Combined with experimental dissociation constants in the range of K_d ~ 100 nM − 100 μM these association rates predict mean dissociation time of FG nup-transport protein complexes of τ_off = (k_onK_d)⁻¹ ~ 0.01-10 ms, shorter or comparable with the typical transit time (1-10 ms) of transport proteins traversing the NPC.

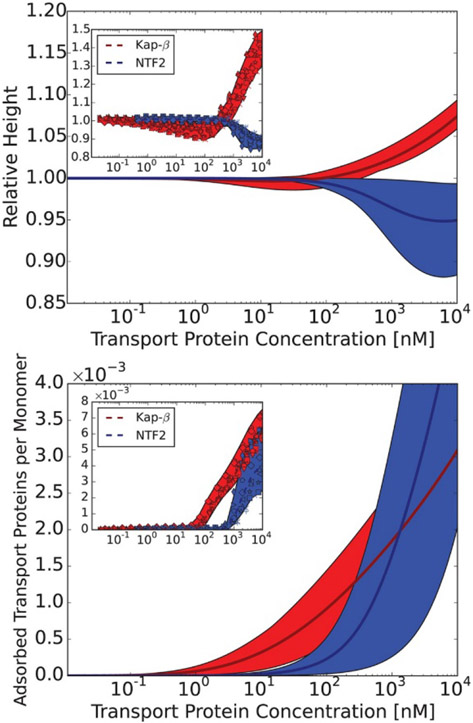
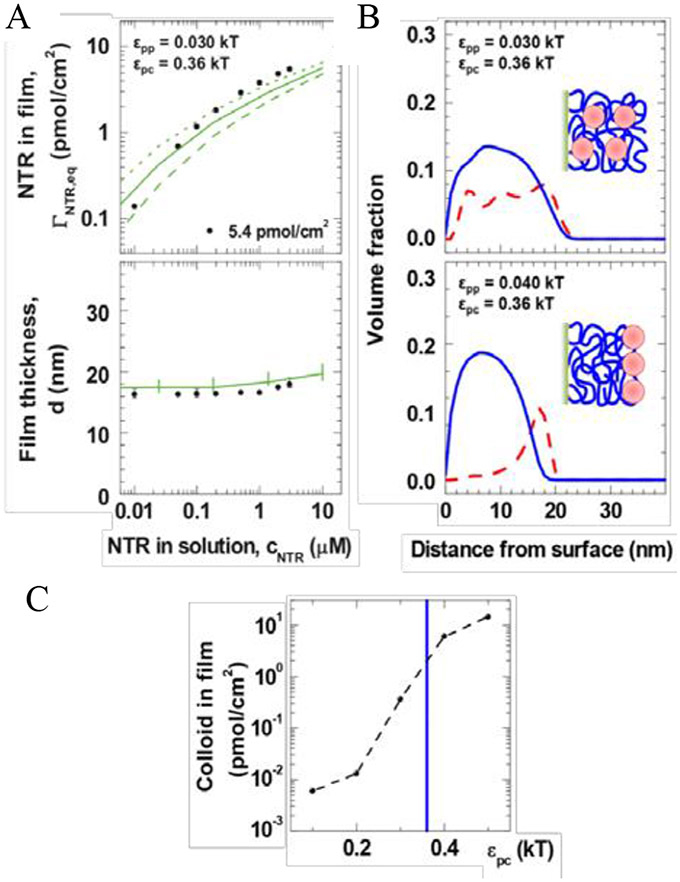
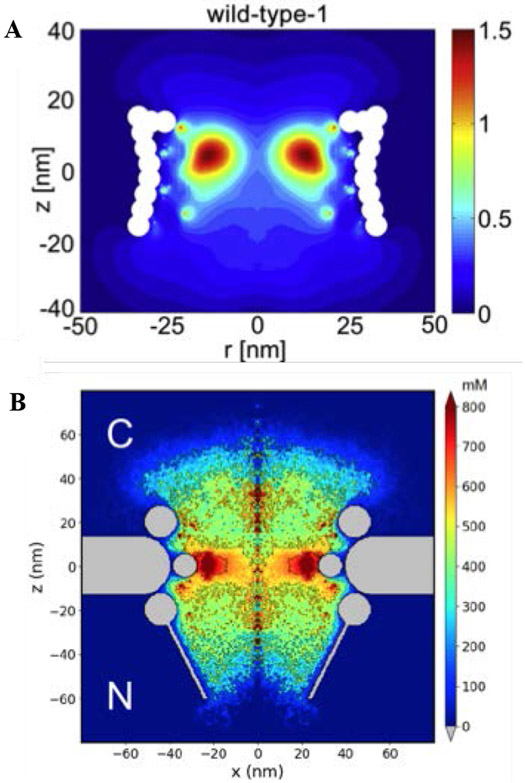
3.4.3. Morphologies of multi-chain assemblies of FG nups and transport proteins in solution

Due to the multivalent and promiscuous nature of the interactions between FG nups themselves and between FG nups and transport proteins, their collective morphologies can be highly sensitive to the environment. In vitro experiments have shown that addition of the transport proteins to the solutions of FG nups promotes aggregation [43,162]. On the other hand, under cytoplasmic conditions (either in cells or lysate), cohesive FG nups have been shown to remain flexible and dynamic which otherwise form aggregates in solutions [103]. The FG nup assemblies and phases in solution serve as rudimentary mimics of the permeability barrier of the NPC, in the sense that they generally exclude inert proteins but are permeable for the NTRs, similar to the selective permeability of the NPC [98,104,164]. The properties of the assemblies of FG nups with the transport proteins were systematically investigated in bulk solutions in [98] and in microfluidic devices in [164], using FG nup aggregates of the type described in Section 3.3.1. Larger cargoes showed reduced penetration of transport protein/cargo complexes into these dense FG nup phases, similar to what is observed in NPC transport [67,77,86,104]. Remarkably, even larger cargoes can permeate dense FG nup assemblies if they are attached to a sufficiently large number of transport proteins [56,104] (Figure 15).

Figure 15.

Phase separation in FG nup/transport protein solutions. Top: (Upper row) Schematic illustration of the transport proteins (brown) with and without bound proteins (green and blue). (Lower row) Fluorescently labeled transport proteins penetrate the dense FG nup “droplet” aggregates as indicated by green fluorescence within the droplets. From left to right, schematically: NTF2 (~40 nm³volume); Importin-β (~100 – 120 nm³); Importin-β with GFP-cargo; Importin-β with GFP-MBP cargo; ternary complex of four Importin-β with GFP cargo. Larger particles, comprising transport proteins with bound cargo (green and blue) are excluded from the FG nup “droplets” Penetration is recovered for large particles bound to sufficient number of the transport proteins. Adapted from [98], permission pending. Bottom: Theoretical phase diagram of the phase separation. The dashed tie-lines connect the co-existing dense and dilute phases located on the boundary of the phase separation region, shown in black line. The permeability of the dense FG nup phase to transport proteins is controlled by the parameter ξ = ν/χ: see text. Adapted from [56], permission pending.

Despite the complexity of the FG nup-transport protein interactions on the molecular level, the behavior of these composite dense phases can be understood within the same conceptual framework that has been used above to describe the behavior of FG nup chains and their assemblies. Because the composition and morphology of an FG nup assembly changes with the penetration of multiple transport protein-cargo complexes, this process can be viewed as a formation of a mixed dense phase through a phase separation mechanism in the ternary FG nup/transport protein/solvent solution. Accordingly, the free energy of Equation (3) can be adapted to account for the entropy of mixing and exclusion of the transport proteins and the FG nups, as well as the attractive interactions between the FG nups and the transport proteins [56,57,60,114,182]. On the mean field level, the latter can be characterized by an average interaction Flory type parameter χ and the appropriate additional term in the free energy, χψϕ, where ψ is the monomer density/volume fraction and ϕ is the density/volume fraction of the transport proteins [56]. Microscopically, χ is roughly proportional to the second virial coefficient of the interaction between the transport proteins and the FG nups, $\chi \sim \int d\overrightarrow{r}\left[1-exp\left(U\left(\overrightarrow{r}\right)∕kT\right)\right]$ where $U(\overrightarrow{r})$ is the microscopic interaction potential that can include both direct and water-mediated interactions [114,120]. This coarse-grained parameter is able to describe a wide variety of (short-ranged) microscopic interaction potentials: e.g., a slightly weaker potential uniformly distributed over the whole surface of the particle may result in the same value of χ as a stronger but anisotropic potential confined only to discrete binding “patches” on the surface.

The overall theoretical phase diagram of such ternary (FG nup/protein/ implicit solvent) mixtures is shown in Figure 15 (bottom). The phase diagram comprises a single-phase region, where the FG nup/transport-protein solutions are stable, and a phase separation region, where the system phase separates into a dense phase in equilibrium with the dilute one [56]. The dashed tie-lines show the pairs of the co-existing phases at different concentrations. Remarkably, the permeability of the dense phase with respect to the transport proteins, as reflected in their density inside the dense phase relative to the outside solution, is largely captured by one parameter ξ = ν/χ, which is equal to the ratio of the transport-protein/cargo complex volume ν to the transport protein-FG nup attractive interaction/binding strength χ. For small ν (small cargoes and/or strong transport protein-FG nup binding), the concentration of the transport proteins in the high-density phase is higher than in the low-density phase, indicating penetration. For large ξ (large cargoes or weak transport protein-FG nup attraction), the tie-lines flip, and the transport protein concentration in the dense phase is lower than in the low-density phase, indicating exclusion, shown in the red lines in the inset. At very high concentrations of the transport proteins and the polymers, there is additional phase separation/de-mixing region [114] , which is not discussed here. Interestingly, at low concentrations, phase separation is promoted by the addition of transport proteins to an FG nup solution even when the pure FG nup solution is stable, while at high concentrations the addition of transport proteins inhibits the phase separation. This might resolve the apparent discrepancies in the literature regarding the effect of transport proteins on the stability of FG nup solutions and aggregates [43,103,162].

Overall, selective permeability of dense FG nup assemblies arises from the balance between the free energy cost of penetration of a transport protein-cargo complex into the dense phase, and the free energy gain due to the attractive interactions between the transport proteins and the FG nups. The penetration cost arises from the work against the osmotic pressure in the dense phase and the entropic costs of polymer re-arrangement, as well as the cost of breaking the cohesive contacts between the FG nups [52,56,57,104,114,198,226]. For large particles and/or weak interaction between them and the FG nups, the penetration cost is higher than the free energy gain, resulting in their exclusion from the FG nup aggregates as shown in Figure 15 [56,104].

This minimal phase separation model explains well the observed densities and composition of both the dilute and of the dense phases of transport-protein/FG nup solutions, as well as their selective permeability patterns, as explained in Figure 15 [56]. These results come with the caveat that the long-term behavior of the FG nup and FG nup/transport protein aggregates is not described anymore by equilibrium physics, as they undergo aging, amyloidization and potentially irreversible chemical cross-linking taking them out of the physiologically relevant realm. Although the precise state of the FG nup assembly within actual NPCs remains unknown, recent experiments in microfluidic devices that enable examination of the liquid state of the FG nup droplets before they mature into less fluid states. In particular, it showed that attachment to transport proteins enables entry into FG nups assemblies for otherwise excluded cargoes, and even very large cargoes based on phage capsids (27 nm in diameter) can enter into a droplet when attached to a sufficient number of transport proteins (up to ~100), in accord with the results of [56,104] and Figure 15. Specific details may vary depending on the density of the FG nups in a droplet.

Thus, although likely incomplete, the equilibrium phase separation model pinpoints the key pertinent variables that control the spatial organization of the transport proteins and FG nup assemblies and provides the foundation for future work towards understanding the internal morphology and dynamics of the NPC.

3.4.4. Assemblies of transport proteins and surface grafted FG nups

As described in Section 3.3.2, assemblies of surface-grafted FG nups resemble the confined geometry of the NPC. Accordingly, they have been used to characterize the interactions between transport proteins and FG nups and the selective permeability of FG nup assemblies. Although the effects of transport proteins on the layer morphology have been a matter of controversy, a consensus picture has emerged [56,57,99,130,171,173]. Similar to the bulk FG nup aggregates, layers of grafted FG nups repel inert proteins such as bovine serum albumin (BSA), while transport proteins and transport protein-cargo complexes can penetrate the layers due to their attractive interactions with the FG nup chains.

At low concentration of the transport proteins in solution, their penetration into the layer does not cause significant changes in the layer height or its overall internal morphology, and they mostly occupy the available space within the layer [56,57,130,182]. However, increasing concentration can result in collective effects resulting in the conformational changes of the layer. At a critical concentration of transport proteins, collective interactions between the transport proteins and the FG nups may cause some overall compaction (also known as “collapse”) of the layer, as indicated by a reduction in assembly height by up to ~10% [56,173,174,182]. The degree of this layer compaction depends on the experimental conditions, such as the grafting density and the type/size of transport proteins and FG nup segments used [56,57]. NTF2, smaller and with less FG binding sites compared to Importin β, causes a higher degree of condensation in FG nup assemblies [56,174]. In general, for the relatively large objects such as the transport proteins, these effects are only moderate. Further addition of transport proteins, after the maximal compaction has been attained, results in the layer swelling [56,57,99,130,172]. These collective morphological changes can also result in a non-Langmuir adsorption curves [56,57,99,130,172]. The potential functional significance of these morphological transitions for in vivo transport is still being debated.

These observations are well described by the minimal polymer models used in Section 3.4.3 for bulk solutions, once adapted to the surface geometry, and treated in a variety of approximations including mean-field approximation, density functional theory, and coarse-grained simulations [56,57,182,227]. The comparison between the theory and experiment is summarized in Figure 16 and Figure 17. Similar to the bulk aggregates, the degree of transport protein penetration is determined by the balance between the free energy cost of insertion and the free energy gain from transport protein/FG nup binding.

Figure 16.

Changes in FG nup layer height induced by the penetration of the transport proteins. Top: relative layer height as a function of the transport protein concentration in solution. Bottom: corresponding number of the transport proteins in the layer. Blue band: theoretical prediction and confidence interval for a large, strongly binding transport protein (Importin-β). Red band: theoretical predictions and their confidence interval for a small, weakly binding transport protein (NTF2). Insets: corresponding experimental data. Adapted from [56], permission pending.

Figure 17.

Distribution of transport proteins within FG nups layers. A: Polymer models (lines) accurately describe the experimental results (symbols) on transport protein (NTR) uptake in grafted FG nup assemblies. B: Moderate changes in FG nup cohesiveness (ε_pp) can lead to qualitatively different distributions of transport proteins (red) in the FG assemblies (blue). C: these models predict a sharp decline in transport protein uptake when the attractive interaction (ε_pc) between FGs and transport proteins drops below experimentally relevant values (blue line). Adapted from [57], permission pending.

The permeability of the surface-grafted assemblies to transport proteins can be regulated by the grafting distance, the size of the transport protein and the interaction strength between FG nups and transport proteins [38,39]. For large proteins, the penetration cost largely arises from the work against the osmotic pressure in the polymer layer and is thus proportional to the volume of the protein; it can be modulated by additional costs of polymer re-arrangement around the transport protein, and the cost of disrupting cohesive inter FG contacts [57,114,226].

The collective effects in the uptake of transport proteins into the layer of grafted FG nups may result in the spatial stratification and formation of a dense region of intercalated FG nups and transport proteins near the grafting surface, reminiscent of the dense phase appearing in bulk solution [182]. However, unlike in bulk solution experiments, surface grafting prevents the system from undergoing a true phase separation, and the resulting spatial inhomogeneity is reminiscent of a “micro-phase separation” of block copolymers [228]. Formation of this dense region correlates with the compaction of the FG nup film (see Figure 16). With further increase of the transport protein concentration, more protein can enter the FG nup film therefore leading to a moderate layer swelling as predicted theoretically and observed experimentally. The effect of concentration dependent protein uptake and layer swelling, although very moderate for large particles such as the transport proteins, is much more pronounced for small particles or mixed solvents, and are related to a phenomenon known in polymer science as “co-non-solvency” [229,230]. The morphologies of FG nup and transport proteins assembles in channel-like geometry of the NPC are discussed in Section 3.4.5 and Section 3.5.

Although difficult to measure experimentally, the predicted stratification of the FG nup assembly into compact and dilute regions is consistent with the observation that transport proteins in dense grafted FG nup layers may be separated into two different populations of transport proteins - one strongly bound with sub-μM dissociation constant and another population with a weaker μM binding, but the validity of these interpretations is still unclear [173] (See also Section 3.2.3).

Furthermore, computational models provide additional insights on how FG nup assembly permeability is influenced by inter-FG cohesiveness, a question that has been a subject of a long-standing controversy in the field [41,56,57,97,114,163,231-233]. In particular, for larger transport proteins, some models predict that moderate increases in FG nup cohesiveness may lead to qualitatively different distributions of transport proteins (see Figure 17), favoring transport protein accumulation on top of instead of inside the FG nup films [57]. Accordingly, transport protein uptake can be highly sensitive to the strength of attractive interactions with the FG nups, as illustrated in Figure 17B,C. While transport proteins readily accumulate within the layer, the uptake drops by several orders of magnitude for similar sized proteins with only moderately lower binding strength to FG nups [57]. These findings are consistent with the “selective phase” model, which postulates that the cohesive FG-FG contacts are important contributors to the permeability barrier of FG nup assemblies [97]. In contrast, at low FG nup densities, the effect of the cohesiveness can be the opposite and facilitates the penetration of transport protein in the film, by enhancing the local concentration of FG repeats (i.e., binding sites for transport protein) in the film [114]. Furthermore, in mixtures of different transport proteins, the conformational transitions and selectivity can be more complicated and still await theoretical explanation [174].

To summarize, relatively simple polymer models capture the morphological behavior of surface-grafted FG nup assemblies, and predict a vastly preferred uptake of transport proteins over inert macromolecules, analogous to NPC transport selectivity. Earlier finer-grained and atomistic models lend additional support to general principles of selectivity transpiring from the simple polymer models, such as its reliance on weak, multivalent interactions of transport proteins with flexible, and moderately cohesive FG-nup assemblies. They also provide molecular underpinning for the coarse-grained parameterization [55,133,234].

3.4.5. Transport proteins in FG nups assemblies in nanopores

As pointed out in Section 3.3.3, confinement within the nanopore geometry of the NPC can enrich the range of morphologies of FG nup assemblies, with potentially important implications for the penetration and translocation of transport proteins through NPC. However, there has been only limited direct experimental information on the uptake and distribution of transport proteins in nanopore-confined FG-nup assemblies. Likewise, most computational work on the NPC has focused on the FG nups, ignoring possible effects of incorporated transport proteins on the overall morphology and transport properties.

Computational models predict that polymer-coated nanopores infiltrated by transport protein particles exhibit many of the behaviors observed in planar assemblies. In particular, for relatively short polymers that do not fill the entire pore, addition of nano-sized particles causes collapse followed by expansion. Changing the particle concentration or solvent composition can be used to “gate” the channel between open and closed states [60,185,203].

For longer polymers such as the full FG nups, multiple possible physical behaviors were predicted [60]. Besides the condensation of polymers in the pore center as discussed in Section 3.3.3, these simulations predict distinct morphologies for transport protein particles. Notably, transport proteins could accumulate at the interface of the condensed FG nup assemblies and the solution; or they could penetrate the assemblies and even form lattice-like structures in the pore under excessive large polymer-colloid attraction. It remains to be determined to what extent the insights obtained from these different equilibrium regimes are most appropriate for the dynamic non-equilibrium environment of the for the NPC. Overall, given the range of qualitatively different behaviors and the large numbers of transport proteins that have been reported in the NPC [7,43], it is likely that the transport proteins are a defining factor for the FG-nup morphologies adopted in the NPC [83,100], as discussed in the next section and in Section 4.2.4. However, it is important to bear in mind that this section only deals with the thermodynamic aspects of NPC specificity. Full understanding of the selectivity of the NPC transport mechanism requires kinetic and dynamical considerations discussed in Section 4.

3.5. Biophysical insights into the morphology of transport channel of intact NPCs

As described in the previous sections, in vitro studies have, to a large degree, identified the key physical principles and molecular features that underpin FG nup assemblies and their interactions with transport proteins. Yet, it remains challenging to extrapolate these insights to gain detailed information about the organization the FG nups and the transport proteins inside the channel of the NPC, and to the nature and the mechanism of the NPC transport. Recent technological advances have made the challenge of probing the internal morphology of intact NPCs more tangible [42-45,119,236,237], albeit still daunting given the large amount of different transport proteins and cargo that can be found even in isolated NPCs [7].

Early experiments used immuno-histochemistry and electron microscopy to image micro-injected gold nanoparticles of different sizes and surface properties in and around the NPC, and provided the first indication of the NPC transport barrier [235]. The results are illustrated in Figure 18, which shows that 30 nm gold particles are essentially excluded from a wide region around the NPC. This exclusion zone indicates the extent of the FG nup “cloud” around the pore. By contrast, particles accumulate in the NPC passageway if they are covered with NLSs (which allows the binding of transport proteins), especially in the regions that are now known to contain FG nups at high densities.

Figure 18.

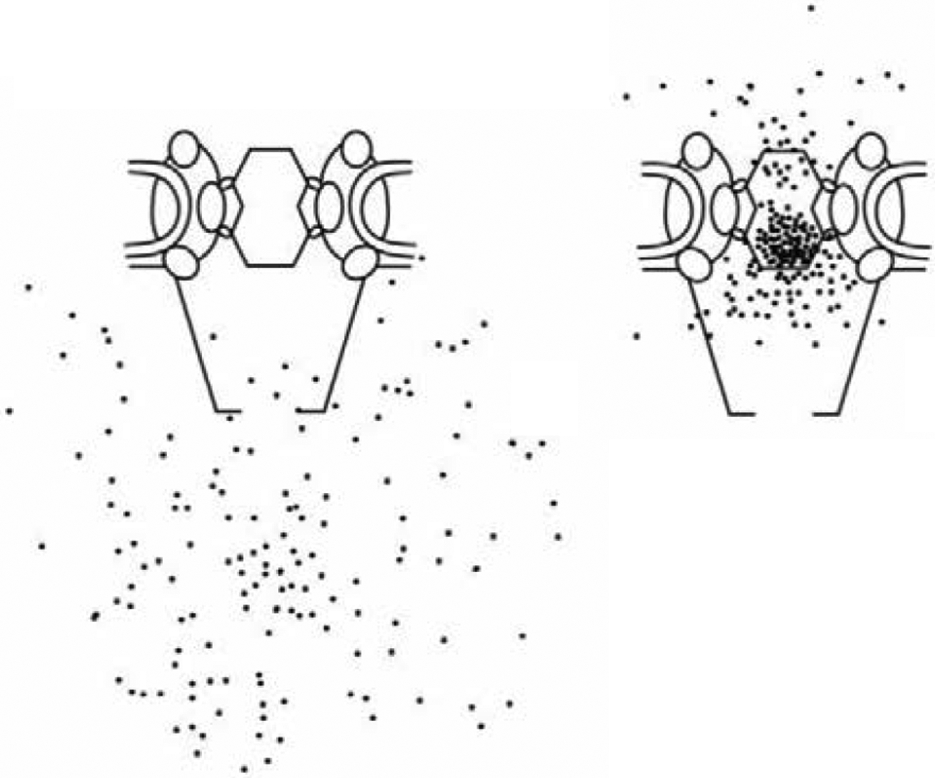
Barrier function of the FG nups in the NPC. Left: distribution of large gold particles around the NPC. Right: distribution of the same size particles covered with NLS, which enables their binding to the transport proteins and thus to FG nups in the pore. Adapted from [235], permission pending.

In recent years, atomic force microscopy (AFM) and fluorescence microscopy techniques have started to provide information about the internal organization of the FG nup/transport protein assembly within the NPC. AFM is unique in resolving the surface topography of individual molecules and molecular complexes at nanometer resolution, without the need for drying, staining, labelling or ensemble averaging. It has been extensively applied to NPCs, often using isolated nuclear envelopes that, in most cases, were mechanically extracted from Xenopus laevis (frog) oocytes [42,45,46,204,238-245].

By indentation of NPCs with sharp tips, AFM probed the NPC surface structure and subsurface nanomechanical features [45,46], and the ensemble-averaged results were consistent with cryo electron microscopy data [241,246]. In addition, the nanomechanical stiffness of the NPC transport channel was consistent with model predictions for a marginally stable FG nup condensate [45,46,247]. However, it remains hard to define if such measurements probe the behavior of FG nups alone or (more likely) the behavior of a mixture of FG nups and transport proteins. At the level of individual NPCs, the surface structures of the transport channel show significant variability from one NPC to the other (Figure 19, top) and remain static over many minutes (in isolated nuclear envelopes, in solution) [35]. This suggests that during the isolation process, the NPCs may have been trapped in a large number of possible arrangements of FG nups, including transport receptors and cargoes inside the transport channel [7].

Figure 19.

AFM imaging of the NPC. Top: High-resolution AFM images of the cytoplasmic side of different NPCs in the same nuclear envelope. Adapted from [46], permission pending. Bottom: Different AFM images of the central channel of a single NPC, indicating dynamic FG nup behavior. Adapted from [42], permission pending. Scale bars: 100 nm (top); 10 nm (bottom). Color scales indicating heights: 0-60 nm (top); 0-4 nm (bottom).

Recent technological advances have improved the temporal resolution of AFM from minutes down to ~0.1 seconds per frame under favorable conditions. This so-called “high-speed” AFM (HS-AFM) has enabled the rapid imaging of NPC substructures such as the cytoplasmic lumen and the nuclear basket [42], which were resolved at nanometer spatial resolution. Its temporal resolution may be sufficient to capture “coarse-grained” views of the NPC morphology and its dynamics [42,204,238]. Indeed, HS-AFM imaging at ~200 ms per frame resolved dynamic behavior within the central channel, attributed to FG nups (Figure 19, bottom) [42]. This observation comes with the technical caveat [204] that it is unclear if and how intrinsic mobility of the nuclear envelope might influence dynamic measurements at specific locations in the NPC lumen.

Interestingly, averaging over successive HS-AFM images resulted in the impression of a dense clump in the pore center [42], which is in good agreement with static AFM measurements of NPCs obtained at lower temporal resolution [45]. This resembles a structure reported by averaging techniques as a “central plug” or “transporter module” [7,101,241,246,248], and is consistent with the hypothesis that dynamic interactions between FG nups might appear as condensates in the pore center at longer time scales [42,45] (see section 3.3).

Complementary to AFM, fluorescence microscopy, including super-resolution microscopy, are tools that identify and localize fluorescently-labeled FG nups and transport proteins inside the NPC [249-251]. In particular, FG nup binding transport proteins were found to preferentially localize at either side of the NPC channel in permeabilized cells, showing a two-lobed distribution along the NPC channel axis, indicating that the FG nups might be distributed non-uniformly along the channel axis [43] (see Figure 20). Such spatial heterogeneity of the FG nups might play an important role in defining distinct, cargo-specific spatial pathways through the NPC [44,252,253]. We return to this question in Section 4.2. That section will also discuss the application of single molecule fluorescence microscopy as a means to study the kinetics of transport through the NPC.

Figure 20.

Distribution of fluorescently labelled transport receptors (Impβ) in the human NPC measured in permeabilized cells. Transport protein binding is associated with specific FG nups (Nup153 and Nup358) at the opposite sides of the transport barrier. In a mutant cell lacking Nup153, transport protein accumulation is severely diminished, especially in the nuclear basket. RanGTP modulates NPC occupancy. Reproduced from [43], permission pending.

Likewise, computer simulations support the picture of the heterogeneous distribution of the FG and its importance for NPC barrier and specificity function [59,62,63,169,170] (Figure 21). In particular, one-bead-per-amino acid models predict averaged amino-acid distributions that show signatures of FG-repeats condensed in a donut-like shape [62,63,169]. Such local variations in FG nup density distribution support the possibility of spatially distinct transport pathways for, e.g., ions and small proteins on one hand and larger proteins on the other [62]. Notably, although some of the detailed simulation models show potential importance of charge and electrostatic interaction in shaping the local FG nup distribution [62,63,110,111]. the overall density distribution of the FG nups is consistent with simple homopolymer and patchy polymer models [60,144,184-186].

Figure 21.

Computational models of the FG nup distribution in the yeast NPC using one-bead-per-amino-acid models. Both models (although with different scaffold geometry and force field parametrization) predict a donut-shaped density profile of FG nups in the pore (in the absence of transport proteins). (Legends) A: Time-averaged FG-nup number density (in nm⁻³); adapted from [62], B: Amino-acid density distribution (in mM); adapted from [169], permission pending.

When interpreting the results of these computational studies, one should bear in mind that FG nup morphology is very likely modified by transport proteins present in the NPC [43,60,83,203]. Hence, future computational evaluations need to consider potential effects the various embedded resident and/or translocating transport proteins on FG nup behavior, keeping in mind the richness of the possible phase diagram and its sensitivity to parameter settings [60].

4. From structure to transport

One fundamental question that surrounds the NPC problem is how the FG nups and transport proteins enable such efficient transport while combining several seemingly contradictory features. On the one hand, its high selectivity relies on the thermodynamically strong and specific interactions between the transport proteins and the FG nups. On the other hand, while transport proteins are enriched within the FG nup assembly, they do not clog the NPC, and individual transport proteins rapidly translocate through its passageway within milliseconds. Finally, NPC transport is robust with respect to structural perturbations and molecular noise, as mentioned earlier.

Similar to the morphological properties of the NPC described in the previous chapter, the foundations of NPC transport dynamics may be understood via in vitro studies interpreted through the lens of theoretical and computational models. In this chapter we summarize the current consensus regarding the physics and the key principles of NPC transport.

4.1. Transport dynamics of the transport proteins within NPC-like FG nup assemblies in vitro.

4.1.3. Diffusion of transport proteins within FG nup assemblies.

Initial studies of transport protein kinetics within macroscopic FG nup environment were performed in hydrogel-like aggregates obtained by irreversible cross-linking of the FG nup chains [94,97,109,161,163,254]. It remains uncertain to what extent the insights from these studies translate to the actual FG nup assembly in the NPC due to differences in internal morphology, confinement and chemical environment [98,161,162]. Nevertheless, micron-sized FG-nup “gels” exhibit rudimentary selective NPC-like sieving properties [96-98,104]. Taken together, these bulk assemblies have provided important insights into the permeability and diffusion of transport proteins within the FG nups.

Protein uptake and transport in FG nup gels can be modeled using a simple kinetic model of entry, diffusion and exit from the FG nup assembly [97], as illustrated in Figure 22. Assuming that the proteins undergo simple diffusion inside the “gel” with a diffusion coefficient D, the steady state flux (per unit area) through a slab of material of width L is $J=\frac{D}{L}(c_L^{in}-c_R^{in})$, where L is the length of the slab and $c_L^{in}$ and $c_R^{in}$ are the (one dimensional) concentrations of the transport proteins at the left and the right edges of the slab, respectively. At steady state, they are related to the outside concentrations of the transport proteins, c_L and c_R, respectively, as $k_{-1}{c}_L^{in}=k_1{c}_L-J$ and k₋₁c_R = J − k₁c_R, where k₁ and k₋₁ are the phenomenological rates of entry into and exit from the gel, respectively [97]. Solving for the flux gives

$$J=k_1\Delta c\frac{1}{2+k_{-1}L∕D},$$ (5)

where Δc = c_L − c_R is the difference in the (one dimensional) concentration of the transport proteins on the different sides of the slab. For an inert protein, the entry rate is low and the exit rate is high, resulting in low flux. For the transport proteins, conversely, the entry rate is high, and the exit rate is low, resulting in high flux. The entry and exit rates depend on the free energy of entry of the particle into the gel: inert particles experience a high free energy barrier, while transport proteins experience a free energy well. The free energy barrier was initially assumed to arise from the cross-linking of the FG nups at the hydrophobic FG motifs [97,109]. However, as discussed in the previous section, the free energy of a particle inside an FG nup assembly likely combines the interplay of both enthalpic and entropic effects [56,57,108].

Figure 22.

Penetration of transport proteins into FG nup “gels”. Top: experimental data, showing penetration of a fluorescently labeled transport protein into a hydrogel (right) as a function of time. Bottom: simple kinetic model of transport protein penetration into and diffusion through a slab of a “gel”. See text for discussion. Adapted from [97], permission pending.

Consistent with the discussion in Section 3.3, permeability of FG nup assemblies with respect to transport proteins depends on the density of FG nup assemblies. At lower density, FG nup hydrogels do not provide a sufficient barrier and allow facile entry of both inert and transport proteins (i.e., they are non-selective) [97]. Accordingly, the measured diffusion coefficients of proteins inside these low-density gels are close to their diffusion coefficients in water. At higher density, FG nup gels permit the entry of transport proteins but severely restrict the entry of inert proteins. When inside high-density gels, it is noteworthy that both inert proteins and transport proteins exhibit similar diffusion coefficients D being on the order of D ≃ 0.1 μm²/s. This is two to three orders of magnitude lower than in a low-density gel, but is consistent with the typical diffusion coefficients in cellular environment [255,256]. It might appear puzzling at the first glance that the transport protein diffusion is slowed down in the FG nup assembly. However, their high thermodynamic partitioning leads to higher concentrations within the FG nup assembly, and therefore facilitates translocation through the assembly.

Further complicating things, the diffusion coefficient – which is treated as a phenomenological constant in this simple description – in general depends on the FG nup density, structure and the interaction strength. How interacting particles diffuse within the interior of such a complex polymeric material still remains an open problem [52,257-270].

Previous theoretical works on diffusion of a patchy polymer through polymer solutions provided the basis for the earlier estimates of the diffusion coefficient of a patchy particle in a polymer solution, which was expected to vary as D ~ e^∣ϵ∣N, where ϵ < 0 is the binding energy of an individual patch [52,271]. However, already for a particle with several interaction patches and moderate binding energies of several k_BT, this prediction results in unrealistically low diffusion coefficients incompatible with in vitro measurements and in vivo translocation times.

Although still not fully understood, multivalency likely helps to reconcile strong thermodynamic binding with the fast mobility of transport proteins in an FG nup milieu. At higher FG nup densities, single particles start to interact with multiple FG nups, allowing the transport proteins to slide in a “millipede-type” motion from one chain to another while breaking only a small number of bonds and remaining tightly bound to the FG nup assembly. Molecular dynamics simulations have provided insights and visualizations of this “slide-and-exchange” mechanism for transport protein motion within an FG nup assembly. In this model, only one binding site is released at each step, enabling the transport protein to progress forward due to the thermal fluctuations of the FG nups, finishing the step with the rebinding at the next available binding site [134]. This way, the transport proteins can have high thermodynamic affinity for the FG nups while maintaining fast kinetics [134].

Using a simplified model of FG nup flexibility and transport protein transfer between FG nups, an analytical expression was obtained for the diffusion coefficient in the bound state in the case of a transport protein with two binding sites (NTF2) [268,272]. Similar ideas were used in [270] for particles with multiple binding sites.

Furthermore, it was theoretically and computationally shown [258] that in solutions of cohesive polymers, increased attraction between the diffusing particle and the polymers can actually increase the diffusion coefficient compared to a neutral particle. This effect occurs because the particle binding to the polymer chains facilitates the dissociation of the transient inter-chain crosslinks that otherwise impede the motion of a neutral particle.

These ideas provide a potential physical explanation for both the importance of high valency of transport factors that allows inter-chain transfers without unbinding, and the flexibility of the FG nups that allows for residual motion even when bound. Chain cohesiveness might enhance the difference in the diffusivity between transport proteins and neutral cargoes. Further synthesis of these ideas is necessary to provide a complete picture of the transport protein translocation through the NPC.

However, diffusion rate is only one ingredient that determines the flux of transport proteins through FG nup coated channels, the other being the rate of release at the channel ends, which is closely related to the thermodynamic permeability discussed in the previous section. In the next section we discuss how these two factors combine to determine the flux through FG nup coated nanochannels.

4.1.4. Nanochannel mimics of the NPC.

Further understanding of NPC transport mechanism can be obtained by exploring nanochannel NPC mimics functionalized with FG nups, which more closely approximate the FG nup morphology and transport kinetics within a pore [23-26,273]. The equilibrium structural properties of the FG nup assemblies in these nanochannel mimics have been discussed in Section 3.3.3.

Depending on the experimental design, these NPC mimics allow measurements of either bulk molecular flux [23], or individual translocations [25,26]. An advantage of measuring bulk flux is the ability to access the high concentration regime where channel crowding may become important. However, in this regime it is harder to obtain information about the dynamics of individual translocation events. Accordingly, experiments that detect single molecule translocation events are able to assess individual event frequencies and translocation (dwell) times but are challenging at very high transport protein concentrations. Moreover, it is often difficult to detect short transport events and to distinguish between successful translocations and abortive events in these experiments [274].

4.1.4.1. Theoretical background: diffusion through nanochannels.

As mentioned in Section 4.1.3, description of the motion of an interacting particle through a polymer assembly on the nanoscale is a non-trivial problem [51,52,257,263-265,267,275,276]. However, as a first approximation, such transport can be thought of as diffusion in an effective free energy potential. The depth, spatial shape of the potential, and effective diffusion coefficient are determined by the interactions between the protein/particle and the FG nups/polymers inside the channel, and the distribution of the latter within the channel. For small particles with relatively weak interactions, the effective potential is roughly proportional to $U(x)\sim B\psi (\overrightarrow{x})$ where ψ is the density of the monomers that make up the polymers and B is the second virial coefficient of the interaction between the particle and the polymer [276], in the spirit of Edwards’s theory [95]. For larger particles, this potential can be related to the free energy of penetration discussed in the context of bulk and surface FG nup assemblies in Section 3, and to the potential of mean force discussed in Section 4.1.2.3.

In a one-dimensional approximation (see Figure 24), the probability of a particle to be at a position x along the channel axis at time t obeys the Smoluchowski equation [49,278]

$$\frac{\partial P(x,t)}{\partial t}=-\nabla J(x,t)\text{with}J(x,t)=-\frac{D}{k_{B}T}\frac{\partial U(x)}{\partial x}P(x,t)-D\frac{\partial P(x,t)}{\partial x},$$

where U(x) is the effective potential and D is the effective diffusion coefficient. As discussed in Section 4.1.3, the diffusion coefficient may itself depend on the binding strength; we return to this question in Section 4.2.3. The same equation describes the density of particles in the channel in the non-interacting particles approximation. The time evolution of this probability distribution can be equivalently described by as hopping between discrete sites with transition rates r_i→i±1 obeying the detailed balance condition $\frac{r_{i\to i+1}}{r_{i+1\to i}}=exp\left(\frac{U_i-U_{i+1}}{k_{B}T}\right)$, using the Master equation approach [278-281] (see Figure 24). These models can be extended to explicitly include the binding-unbinding kinetics of the proteins by considering the protein diffusion in the bound and the unbound states [49,268,270,272,282].

Figure 24.

Schematic illustration of diffusion and hopping models that describe particle translocation through a channel. See text for discussion. Adapted from [277], permission pending.

These models of in-channel diffusion, illustrated in Figure 24 can be coupled to the particle diffusion outside the channel, and allow one to calculate the transport properties such as the translocation probability, translocation time and particle flux, under various assumptions mimicking different experimental conditions [49,277,283,284]. The translocation probability (the probability of a particle to successfully traverse the channel to the other end rather than returning back in an abortive attempt) is approximately

$$P_{\to }=\frac{1}{2+\alpha \frac{D_{out}}{R{D}_{in}}\int dx{e}^{U(x)∕k_{B}T}},$$ (6)

where R is the channel radius, and D_in and D_out are the diffusion coefficient inside and outside the channel, respectively; α is a numerical prefactor that depends on the geometry of the channel entrance and the particle shape. This equation is the direct analogue of the one-dimensional flux equation in slab Notably, the expression for the translocation probability is relatively insensitive to the exact shape of the potential U(x). In order to account for the enhanced release of transport protein from the potential well facilitated by RanGTP in the nucleus equation (6) can be modified by modifying the corresponding exit rates or potential shapes [49,220]. The limitations of this single particle expression can be recognized by noting that the maximum translocation probability would – unrealistically – occur for an infinitely negative potential well U(x). In reality, for very strong interactions the channel becomes jammed, either due to “freezing” of the particle motion due to low diffusion coefficients, or due to crowding present in deep wells [49,268,276,277,285].

The single-molecule translocation probability can be related to the bulk flux through the channel by noting that equation (6) also describes the particle density in the channel in the non-interacting particle approximation. At steady state, for particles that do not interact with each other, the flux through the channel is

$$J=J_{in}{P}_{\to },$$

where J_in = k_inc is the flux impinging onto the channel entrance from a solution containing particles at a concentration c (assuming zero concentration at the other side). This flux equation becomes similar to Equation (5) in the slab geometry with the identification k_in = k₁·πR² and $k_{-1}=\alpha \frac{D_{out}}{LR}\int dx{e}^{\frac{U(x)}{k_{B}T}}$. For simple diffusion-limited entry, k_in can be approximated as k_in = βD_outR, where β reflects the shape of the channel opening [286-288]; if the interaction potential stretches outside the channel, that enhances the effective capture radius is enhanced by a factor approximately equal to $\sim {\left(R{\int }_R^{\infty }\frac{dr}{r^2}{e}^{-\frac{U(r)}{k_{B}T}}\right)}^{-1}$ [289,290].

The general expression for the translocation time is more cumbersome [277,280,291]. For the simple case of a uniform trapping potential inside the channel, U(x) = −E < 0, the translocation time is approximately $T_{\to }\simeq \frac{RL}{D_{out}}{e}^{\frac{E}{k_{B}T}}$. Under these circumstances, the translocation time increases exponentially with the interaction strength E, as the probability of a fluctuation that takes the particle out of the potential well becomes exponentially small [289]. In the opposite situation of a repulsive barrier inside the channel, the translocation time (for those particles that do translocate) is approximately $T_{\to }\simeq \frac{L^2}{D_{in}}$. In this regime, although the successful translocations are rare, those that do occur are independent of the height of the free energy barrier in the pore. For simple diffusion models, the distribution of both the successful and abortive translocation times typically has exponential tails [280,289,292].

Because the translocating particles remain longer in a deeper potential well, it is no surprise that the translocation time increases with the potential depth. Less intuitively, the translocation probability (and therefore flux) also increases with the potential depth. This effect, sometimes known as facilitated diffusion, has been noted in a variety of contexts [282,293,294]. It occurs because a deeper potential well leads to a local non-equilibrium enhancement of particle concentration in the channel and therewith to an enhanced flux through the channel. In other words, a deeper potential increases the translocation probability because it reduces the chance of abortive exit after the channel entry. More intuitively, a decrease in the diffusion coefficient inside the channel D_in decreases the translocation probability. Although the exact dependence of D_in on the interaction strength is still unknown, a number of models predict that it is decreased by the binding to the polymers (see Section 4.1.3). In this case, this effect can balance the increase in the translocation probability due to binding, resulting in the maximization of transport at an optimal interaction strength [268,272]. This may provide the foundation for the transport selectivity of the NPC, whereby translocation though the NPC is only favored for transport protein-cargo complexes with an effective affinity in a certain range (Figure 25).

Figure 25.

The ratio of the predicted steady-state flux of a transport protein (illustrated as blue arrow) to that of a non-binding protein of the same size (illustrated as orange arrow). The effective diffusion coefficient in the bound state inside the channel decreases with the binding affinity of the transport protein to the FG nups/polymers, resulting in a non-monotonic dependence of the flux through the NPC-like channel on the interaction strength. See text. Adapted from [268], permission pending.

These theoretical principles have been validated in micro-channel/micro-particle experiments with optically generated potentials [295,296].

4.1.4.2. Specificity of NPC mimics at the single molecule level

These simple concepts have been useful in analyzing the transport through NPC mimics. Results obtained from FG nup-functionalized solid state nanopores are illustrated in Figure 26 [26]. Electrochemical scanning techniques, which detect temporal decreases in ionic flux due to a “blockade” caused by a translocating particle, were used to detect single molecules passing through the nanopore. The main caveats of these techniques are that both successful and abortive translocation events cause a (transient) blockade, and that the electric driving force may cause an additional bias to the transport [25,196,274]. Nonetheless, these systems have provided powerful tools to test the theoretical concepts that describe selective transport in nanochannels and their application to the NPC.

Figure 26.

Translocation of transport proteins through nanochannels detected on the single molecule level. A, B: time traces of the ionic flux. The translocation of the transport protein Importin-β through the channel temporarily blocks the current. C: For the transport protein (Importin-β), the blockade times (dwell times) are longer in an FG nup (Nup98) modified pore than in a bare pore. The translocation frequency, however, is similar to that of the bare pore, indicating that the FG nup covered pore is permeable to the transport proteins. D: For the control protein (BSA) which does not interact with the FG nups, the translocation frequency is severely diminished compared to the bare pore and compared to the transport protein, indicating a selective permeability barrier. Adapted from [26], permission pending.

These experiments showed that the dwell time distributions of the transport protein Importin-β and the control protein BSA were essentially the same in bare pores, as expected for proteins of similar size and charge. The presence of FG nups, however, led to a significant reduction in the number of entry events for BSA, thereby reinforcing the notion that the FG nups serve as a barrier for inert proteins. By contrast, the number of transport protein translocation events through an FG-nup coated pore was similar to the bare pore, although on average, each translocation event was longer. These observations support the overall conceptual picture of NPC transport whereby the FG nup assembly serves as a barrier for neutral proteins, while enhancing transport of the transport proteins [25,26].

4.1.4.3. Effective potential in FG nup functionalized nanopores

The effective potential for translocating cargoes within NPC mimics is determined by the spatial distribution of the FG nups within the nanochannel. Although hard to directly determine experimentally, this effective potential can be estimated from simulations of particle translocations through FG nup covered channels by calculating the ‘potential of mean force’ (pmf) of a translocating particle [25,63,297]. The pmf at a position x within the channel is defined as the amount of work required to (adiabatically slowly) bring a particle from infinity to x, and can be calculated from the steady state distribution function P(x) of the particle in the channel, pmf(x) ≃ k_BTln(P(x)); it is also related to the free energy of insertion ΔF, discussed in Section 3.4 [226]. The pmf can serve as a proxy for the effective potential with the caveats that: 1) for fast transport the force profile experienced by the particle might deviate from that dictated by the equilibrium pmf, as the FG nups and the particle might sample only a restricted set of their configurations during the transport time; and 2) the effective potential can also be modified by the presence of multiple transport proteins in the pore.

In particular, ref. [25] used the one-bead-per-amino-acid model of the FG nups, described in Section 3.3.3, to compute pmf profiles for the transport protein (Kap95) and a control protein (mCherry) along the central axis of a 45 nm nanopore, coated with either a cohesive FG nup (Nsp1) or a less cohesive mutant (Nsp1-S) that also interacts more weakly with the transport protein, as shone in Figure 27. Inside a pore coated with the wild type FG nup (Nsp1), a pronounced free energy barrier was found for the control protein (blue line), while the transport protein experienced an attractive energy profile (black line). By contrast, the pmf curves for the control (green curve) and transport protein (red curve) for the mutant Nsp1-S pores were found to be similar, consistent with the non-selective nature of the mutant pore. The detailed shape of the effective potential depends on the force field that parametrizes the hydrophobic, electrostatic and steric interactions between the FG nups and the assumed properties of the particles that model the transport proteins [25,53,54,63,110,297]. However, the overall shapes and strengths of the effective pmf potentials are consistent across different models of varying degree of coarse-graining and parameterization choices.

Figure 27.

Effective potential (potential of mean force, (pmf)) calculated for different cargo types translocating through nanopores functionalized with FG nups. Inert particles (tCherry protein) experience a high free energy barrier in FG-nup (Nsp1) coated pores (blue line), whereas the transport proteins (Kap95) experience a lower barrier (black line). No such contrast is observed when the pore is coated with a less cohesive mutant (Nsp1-S) (red and green). Reproduced from [25], permission pending.

General principles of transport selectivity are emerging from the combined analysis of the equilibrium selectivity and permeability of the in vitro assemblies discussed in Section 3.4, and the analysis of the kinetics and energetics of translocation described in Section 4.1.4.1. In the main, permeability of an FG nup covered channel is determined by the effective cost of penetration of a particle into the FG nup assembly inside the channel. The probability of its subsequent translocation and therefore the flux through the channel can be understood using kinetic models for diffusive transport through effective potential barriers/wells, informed by the pmf of the particle in the channel. Attractive interaction with the FG nups in the channel, resulting in a deeper potential well, enhances the transport through the channel at the expense of increased individual translocation times, as illustrated in Figure 26 and Figure 27.

Overall, these general principles of transport specificity apply also to less explicit NPC mimics [27] and other synthetic nanochannels, even quite removed from the NPC in terms of their molecular components [146,298], as well as biological channels such as bacterial porins [299-302]. For instance, NPC mimicking nanochannels functionalized with synthetic polymers are selective with respect to the cargo interaction with the polymers in the channel, confirming the basic principles of NPC operation [27].

4.1.4.4. Transport protein crowding inside the channel

Given that the NPC transports multiple molecules simultaneously [88,303,304] and is continuously occupied by multiple transport proteins [43,83,305], the single-molecule analyses in the previous section may not adequately account for the crowded conditions that apply in the NPC. The question of crowding features prominently when considering the specificity of the NPC. Diverse species such as export, import and mRNA transport complexes interact with the NPC, presumably in different ways. On the other hand, there are many other proteins in the dense environment of the cell, present at concentrations that may be several orders of magnitude higher than those of transport proteins, and that can interact with the NPC non-specifically [103,206,222]. Yet these are efficiently filtered out, without clogging the NPC. In the more general context, the question of specificity and throughput in the presence of non-specific competition is important for the design of artificial nano-channels and biosensors that are capable of molecular sorting and detection under realistic conditions without fouling [193,306,307].

To include the competition for space and binding sites inside the channel, the translocation of particles can be described via extensions of the hopping models described above, introducing full or partial exclusion between particles at the same site. A number of methods have been devised to treat such scenarios, using ASEP (asymmetric exclusion processes) models and other methods [277,308-311]. In the mean field approximation, the rate equation for the average occupancies n at site i can be written as

$${\stackrel{.}{n}}_i=-r_{i\to i+1}{n}_i(1-n_{i+1})-r_{i\to i-1}{n}_i(1-n_{i+1})+r_{i+1\to i}{n}_{i+1}(1-n_i)+r_{i-1\to i}{n}_{i-1}(1-n_i),$$ (7)

where the r_i→j refer to transition rates from site i to site j (see Section 4.1.2.1 and Figure 24 ). The models can be used to calculate the steady-state fluxes, and can be extended to compute single-molecule quantities such as translocation times [281,292,312-314].

As explained above, the probability of translocation increases with the time that particles remain in the channel. However, longer residence times can lead to crowding and eventual of blockage of the pore entrance, resulting in the saturation of the flux as a function of the concentration [49,277,285]. Accordingly, stronger particle-channel interactions initially increase the transport probability but lead to channel jamming and reduction in the flux at very deep potential wells. Balancing these two effects, the channel throughput may be optimized at a certain value of the potential depth/exit rate as shown in Figure 28. Interestingly, this implies that the flux through the channel is not maximized by attaining a relatively flat potential profile, as it might be expected. Instead, it is maximized for a net negative potential well [49,277,285]. These theoretical principles have been validated in micro-channel/micro-particle experiments with optically produced potentials, as well as in other experiments [295,296].

Figure 28.

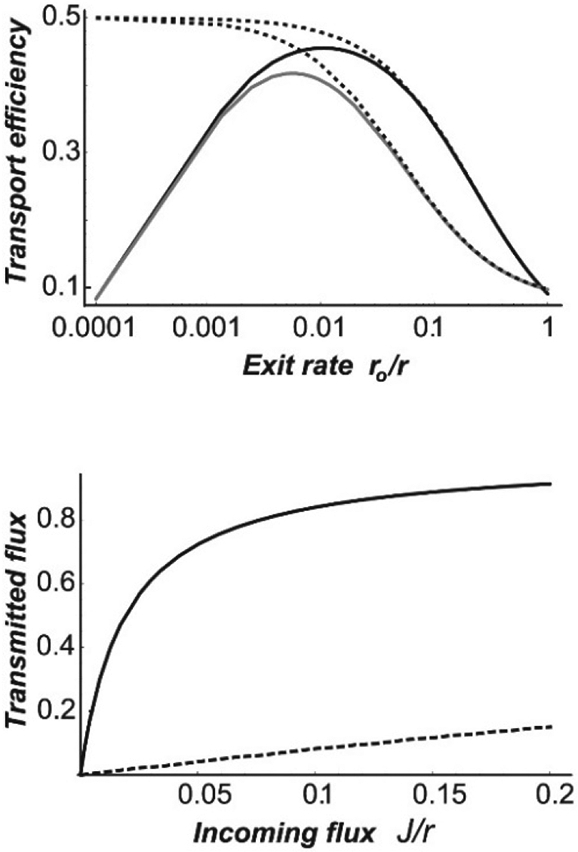
Effects of trapping in the channel on transport efficiency and transmitted flux. Top: transport efficiency, defined as the ratio of the transmitted flux to the incoming flux as a function of the interaction strength in the channel The exit rate $\frac{r_o}{r}\simeq exp\left(-\frac{E}{k_{B}T}\right)$ where E is the potential well depth; r is the hopping rate within the channel.. Bottom: Transmitted flux as a function of the incoming flux. Solid line: particles with strong attraction to the channel. Dashed line: neutral particles that do not interact attractively with the channel. Reproduced from [312], permission pending.

Crowding caused by transport proteins could also explain the specificity of transport when multiple protein species are present, and when the transport proteins compete for space and binding sites in the channel with large numbers of other non-specific molecules. Some of these questions were investigated with FG nup functionalized nanoporous membranes described in Section 3.3.3 [23] and uncovered non-trivial non-linear interactions between fluxes of different species. Namely, the transport of inert control proteins was significantly reduced by the presence of transport proteins whereas the presence of inert proteins facilitated the translocation of transport proteins [23]. These results can be understood within the simple kinetic models described in equation (7) and Figure 24, and were extended by multiple species containing a mechanism of preventing the transport of non-specific competitor molecules [50]. Under these conditions, transport proteins, that bind strongly within the channel (see Section 4.1.4.3 and Section 4.2.4), reduce the probability of the translocation of non-specific proteins. Typically, if a specific molecule binds tightly to the channel and is followed by a non-specific molecule with loose interactions, the latter will likely diffuse out of the channel before the specific transport protein moves through. On the other hand, if the transport protein is followed by another transport protein, it is likely that the latter will linger long enough for the first one to clear through. Thus, the non-specific molecules are unlikely to translocate through the channel, and their accumulation near the entrance creates an additional density exclusion gradient that enhances the translocation of the specific transport proteins by preventing their return to the cis compartment [50]. This indicates that the specificity conditions strongly depend on the multi-species composition of the cargoes transported through the channel.

These theoretical predictions are in good agreement with the experimental results of Jovanovic-Talisman et al. [23]. Moreover, the competitive selectivity effects have been confirmed in other work using synthetic nanoporous materials for molecular separations [193,199]. Conceptually similar phenomena have been described in ion channels, known as “anomalous mole fraction effect”. In this case, ionic fluxes in the mixtures of ions are not proportional to the molar concentrations of the ions in the feed solution, because the differences in their transport kinetics are amplified through non-linear density coupling within the channel [315-317].

4.2. Physical insights into transport by NPCs in the cell

Actual NPCs are significantly more complex than even the most elaborate in vitro mimics. Nevertheless, analysis of transport phenomena in reconstituted FG nup/transport protein assemblies and nanofabricated NPC mimics using physical models helped identifying the key principles of transport and resulted in computational tools that together provide an important framework for the understanding of the structure and the function of NPCs in the cell.

4.2.3. Passive permeability barrier of the NPC

According to the common consensus, one primary function of the FG nup assembly in the NPC is to provide a permeability barrier and filter for undesirable cargoes that are neither bound to the transport proteins nor specifically bind the FG nups directly [67,75-77,235].

Early investigations of the passive permeability barrier were performed using electron microscopy to visualize the localization of (PEGylated) gold nanoparticles that were micro-injected into living cells on either side of the nuclear envelope, as illustrated in Figure 29 [235]. Whereas small particles were able to translocate through the NPC, large particles did not penetrate the NPC to a measurable degree even at long times after injection.

Figure 29.

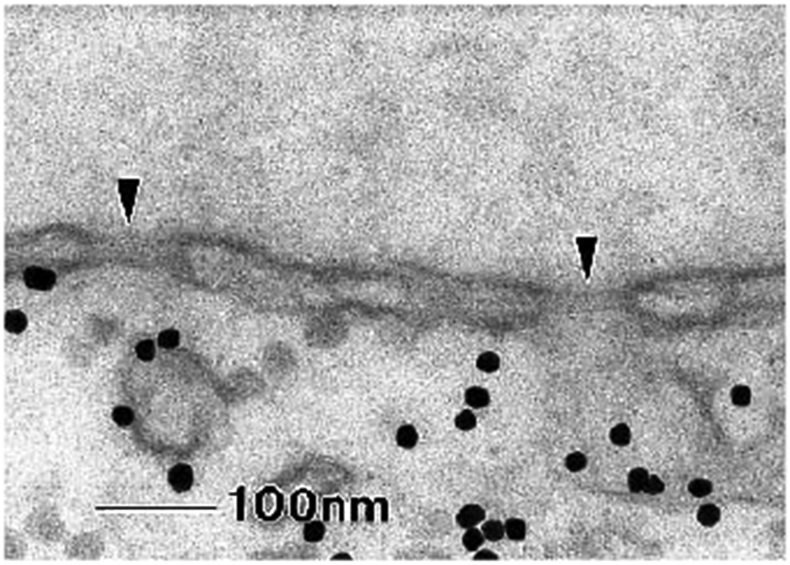
EM image of the nuclear envelope perforated by nuclear pores (indicated by black arrows). Black dots are the gold nanoparticles micro-injected into the cell. Reproduced from [235], permission pending.

Further quantification of the size dependence and cutoff for passive permeability was provided using an ex vivo setup [76]. The nuclear envelope of Xenopus laevis (frog) was mechanically extracted from oocytes and spread out on a nanoporous surface, resulting in co-localization of some of the NPCs with the nanopores. The permeability of the NPC was assessed by measuring the flux of fluorescently labeled dextran cargoes through this composite structure. It was found that the flux of the passive cargoes through the NPC diminished with the cargo size and became almost non-existent at a molecular weight of around 40 kDa, corresponding to a particle radius of approximately 2.5 nm [76].

The results were further refined in permeabilized cells using protein cargoes of different sizes [77]. These studies showed that the 40 kDa cutoff is not absolute, and the flux persists even for larger cargo, although with a strong size dependence. Other studies [67,75] compared the passive transport through the nuclear pore in yeast for different mutant cell lines with different FG nup density and cohesiveness. These yeast experiments are summarized in Figure 30, bottom. However, direct comparison of the results of these independent experimental studies using different methods should be undertaken with caution. Nevertheless, in spite of the wide variety of cell types and experimental techniques in these studies, the size-dependence of the passive permeability appeared remarkably consistent.

Figure 30.

Transport of passive particles through the NPC. Top: Normalized kinetic constant k of cargo accumulation the nucleus as a function of the particle Stokes radius R. Red line: fit with the model of weighted diffusive fluxes through three independent fluid channels. Adapted from [77], permission pending. Bottom: inverse of the normalized kinetic constant of the neutral proteins transverse into the nucleus as a function of their molecular weight MM ~ R³. Adapted from [75], permission pending.

Initially, passive fluxes of neutral particles were interpreted based on the assumption that the NPC passageway can be viewed as a collection of separate parallel liquid filled transport channels [76,77], inspired by early structural data [318].

These were superseded by theories based on the current knowledge of the physics of the FG nup assembly and kinetics transport described in the previous sections. Following the discussion of the FG nup covered nanochannels in Section 4.1.2, the experimental findings in NPCs in live cells could be interpreted in terms of the effective free energy profile that is experienced by the translocating particles. For neutral cargoes, the lack of affinity for the FG nups inside the NPC passageway results in a high (positive) effective potential barrier U(x) for diffusing particles. According to equation (6) the flux in this case is proportional to

$$J\propto \frac{1}{2+\alpha \frac{D_{out}}{R{D}_{in}}\int dx{e}^{\frac{U(x)}{k_{B}T}}}\simeq e^{-\frac{\Delta G}{k_{B}T}},$$

where $\Delta G\equiv k_{B}Tln\left(\int dx{e}^{\frac{U(x)}{k_{B}T}}\right)>0$ is a measure of the height of the free energy barrier. In this regime of barrier-limited penetration, the expression for the flux derives from the same physics as the classical Boltzmann, Arrhenius, Eyring, Polya and Kramers expression for barrier crossing rates in chemical reactions. In case of NPC, the distance along the channel axis serves as the “reaction coordinate” [25,75,319].

Both the one-bead-per-amino-acid model of Ghavami et al. [297] and the homopolymer model of Timney et al. [75] found that the free energy barrier ΔG scales with the particle radius as R^a, where a~1-2. These observations are consistent with the theoretical estimates of the insertion cost of a neutral particle of radius R into a polymer assembly [226,320]. However, the exact scaling of the experimental results is still not fully understood due to the limited size range of the probed particles, experimental errors, and discrepancies between theory and experiments.

The transport barrier can be modulated, both in experiments and in computational models, using mutants, which are less cohesive and form a lower density of the FG nup cloud inside the pore [67,75]. As expected on theoretical grounds, the effective barrier for transport is lower in these mutants, and passive cargoes consequently exhibit higher flux. More specifically, Popken et al. [67] computed the FG nup density distribution in the model yeast NPC for different FG nup strains, and found an approximately linear decay of the experimental permeability with the computed average protein density in the center of the pore. Hence, the passive permeability can be related to the density and the intermolecular interactions of the FG nups in the NPC, described in Section 3.

4.2.4. Kinetics and energetics of the facilitated transport through NPCs in cells.

Here we describe how the models and concepts arising from the study of in vitro mimics also provide invaluable input into the analysis of facilitated/active transport in living cells.

Transport through the NPC is both selective and rapid, producing fluxes of hundreds of molecules per second per NPC [86,89]. The high specificity of the NPC is illustrated in Figure 31, which illustrates the difference between the import of cargoes that possess a NLS (i.e., can bind transport proteins) and cargoes with a mutation in this sequence (i.e., do not bind transport proteins).

Figure 31.

Illustration of a high selectivity of nuclear import. Left: nuclear accumulation of fluorescently (red) labeled cargoes possessing a NLS that enables them to bind the import proteins. Cell nuclei with accumulated cargo appear red. Right: import of the same cargoes with a mutant NLS sequence that precludes their binding to transport proteins. Adapted from [78], permission pending.

It has been long believed that the interactions between the transport proteins and the FG nups arise predominantly from the phenylalanine binding to the hydrophobic grooves on the transport proteins. However, as mentioned in Section 3.4.1 the exact number of binding sites on the transport proteins is not fully known, [107,205,210,211,321]. Moreover, recent experimental work has established that the permeability of the NPC with respect to various cargoes is determined not only by the hydrophobic binding sites on their surface, but also by residues that form charged, cation-π, and π − π interactions with the FG nups. Accordingly, artificial cargoes can be engineered to tune their permeability into the NPC based on their surface properties; typically, negative, hydrophobic and aromatic stacking residues promote transport, while positive residues impede transport [96,97,214,233,322,323], summarized in Figure 32. This is consistent with computational predictions [63] shown in Figure 33, which indicate that transport probability may be tuned through the balance between hydrophobic and charged residues on the cargo surface. Taken together, these experimental data and their theoretical analysis indicate that the specificity of the transport protein/FG nup interaction relies on the balance of hydrophobic and charged interactions.

Figure 32.

Surface properties are responsible for the efficient translocation of cargoes through the NPC; see text. Reproduced from [96], permission pending.

Figure 33.

Single molecule studies of NPC transport. Top left: trajectories of fluorescently labeled transport protein in the vicinity of the nuclear envelope. Red: successful translocations. Blue: abortive translocation. Right top: snapshots of a movie of a successful and an abortive translocation. Bottom panel: distributions of successful (left) and abortive (right) transport events. Adapted from [78], permission pending.

However, these bulk measurements of fluxes do not provide information about the translocation dynamics at the single-molecule level.

First characterization of the dynamics of translocation of individual transport proteins originated from single molecule tracking in [78,324], and [81,91] (Figure 33) and established two important points. First, they directly confirmed that the translocation of transport proteins is a stochastic process, consistent with the model of thermally activated diffusion. In particular, it was observed that the translocations can be abortive whereby the transport protein returns to the cytoplasm rather than translocating into the nucleus. Second, the observed translocation times obeyed a distribution with an exponential tail, with a characteristic decay time of several milliseconds for both successful and abortive events. Notably, NPC mimics have been able to recapitulate these the durations of translocation events (Section 4.1.2), indicating that they capture the most salient features of NPC transport dynamics.

To further probe NPC transport dynamics, large cargoes have been constructed by fusing multiple proteins or using quantum dots [220,325,326]. These experiments also serve as the first step in understanding how large cargoes, such as large mRNA particles or viral capsids, navigate the NPC [12,327-329].

Musser and coworkers [220] used a large tetrameric protein complex with a total molecular weight 465 kDa, or approximately 10 nm in diameter. Each subunit carried one NLS, which allowed to load different numbers of transport proteins onto the construct and thus tune the strength of its interaction with the NPC. Using single molecule fluorescent microscopy, translocating complexes could then be tracked individually in permeabilized cell assays. This provided information about spatial densities and distributions of the accumulated cargoes in the NPC under different experimental conditions, such as the presence or absence of RanGTP, including statistics of successful and abortive transport events and their translocation times. The results were analyzed in terms of diffusion in the effective potential model described in Section 4.1.4. The inferred effective potential showed a barrier in the middle of the pore along the transport axis, and two potential wells at the nuclear and the cytoplasmic “vestibules” of the NPC. When the number of transport proteins attached to the cargo was increased, the barrier became lower due to stronger interaction of the construct with the FG nups, in accord with the expectations. Addition of RanGTP to the system increased the transport, likely caused by the reduction of the potential at the nuclear vestibule. This observation is consistent with RanGTP function of catalyzing the release of the cargoes from the NPC.

In a complementary approach, Weis, Liphardt and co-workers used quantum dot nanoparticles, conjugated with up to ~40 transport proteins, resulting in a construct of 30-40 nm in size [325]. The transport and translocation of the nanoparticle through the NPC was tracked using optical (fluorescence) microscopy. The quantum dot experiments are in good agreement with previous experiment and also support the existence of the permeability barrier/bottleneck at the center of the pore flanked by “docking” areas on the nuclear and cytoplasmic sides (see also Figure 20).

More recently, [326] used very large cargoes based on viral capsids that can reach up to 30 nm in diameter and carry up to 100 NLS attached transport proteins. These studies support the previously identified general trends - import efficiency increased with the number of transport proteins, and larger cargoes required more attached proteins for efficient transport than the smaller ones. Analysis of these results in terms of transport in an effective potential similar to [220] was also consistent with the existence of a central free energy barrier and a cytoplasmic “docking”/“vestibule” regions.

Notably, simulations of the FG nup distribution in the pore also predict higher effective potential barrier for cargoes at the center of the pore, shown in Figure 34 [62,63], although the simulation parameters do not fully resemble cellular conditions.

Figure 34.

Inferred effective potential profiles along the axis of the NPC from single molecule trajectory tracking. Dashed lines: neutral particles. Black lines: particles with weak attraction to the FG nups. Red lines: particles with strong attraction with the FG nups. Reproduced from [330], permission pending. Bottom panel: Computational effective potential profile (pmf) along the NPC axis for particles of different surface properties. Reproduced from [63], permission pending.

Overall, in vivo studies support the picture arising from the in vitro experiments. The selectivity of the NPC transport is largely determined by the thermodynamic free energy of transport protein penetration into the FG nup assembly. This free energy defines an effective potential for diffusion inside the pore, which comprises the free energy cost of penetration due to entropic and osmotic effects, as well as the cost of breaking the cohesive interactions between the FG nups, which is balanced by the binding between the transport proteins and the FG nups.

When attempting to relate transport efficiency and speed to the molecular affinity between transport proteins and FG nups, various problems arise that require corrections to the simple picture of diffusion through an effective potential. One reason is that interactions not only determine the effective potential, but also affect the effective diffusion coefficient. Although it is still unknown how the diffusion coefficient depends on various parameters, the dynamic considerations can mod late the thermodynamic selectivity picture [52,257-262,267,268].

Initially, the short translocation times caused consternation because of the strong equilibrium effective binding affinities between the FG nup assemblies and transport proteins – sometimes known as the “transport paradox” [134,206,219,331]. As explained earlier, this apparent inconsistency can be attributed to the multivalency of the interactions between transport proteins and FG nup and the FG nup flexibility, allowing the transport proteins to slide in a millipede-type motion from one to another while breaking only a small number of bonds, resulting in relatively high diffusion coefficients observed in vitro and in vivo as well as the high release rates from the pore ends [103,134,224].

Additional factor is the potential spatial heterogeneity of the FG nup assembly in the NPC that has been deduced from both in vitro and in vivo studies [7,36,43,100,101,173,220,332,333]. Because the effective affinity of the transport proteins/FG nup, binding strongly depends on the local FG nup concentration (see Section 3.4), it has been hypothesized that NPC regions with low FG nup concentration contain a population of transport proteins with a lower effective binding affinity and thus higher mobility, which are predominantly responsible for the fast cargo translocation through the NPC [100,101]. Transport protein crowding might be also contributing to the resolution of the paradox (see next section). However, full quantitative understanding of the NPC transport process in its entirety is still lacking, and further computational and experimental work is necessary to fully understand the mechanism of transport protein motion through the FG nup network.

3.4.2. Effects of transport protein crowding on NPC transport

Unlike the case of many other protein transporters, protein translocation through the NPC does not occur one-by-one. Due to their affinity to the NPC interior, transport proteins tend to accumulate within the pore, as illustrated in Figure 35, which shows enrichment of the fluorescently labeled transport protein NTF2 within the nuclear envelope [23]. Similar accumulation can also be observed for other transport proteins, such as Importin-β, with tens and possibly hundreds present simultaneously in the NPC (e.g., [43]). Furthermore, NPC contains many different types of transport proteins, and is engaged in bi-directional processes, including cargo-carrying import proteins translocating into the nucleus, RanGTP-bound import proteins returning to the cytoplasm, export proteins, and mRNA export particles [6,9].

Figure 35.

Accumulation of transport protein NTF2 in the nuclear envelope. Top: cell nucleus (white) surrounded by fluorescently labeled transport protein NTF2 in the cytoplasm. Bottom: after 30 minutes, significant fraction of the transport proteins accumulates in the NPCs at the nuclear envelope, as indicated by the bright red rim. Adapted from [23], permission pending.

While the presence of multiple transport proteins increases the NPC throughput on the one hand, it also has a potential to block the pore. It remains to be fully understood how the NPC is able to maintain high throughput and selective bi-directional transport under such conditions, and different investigations provide somewhat contradictory evidence. One of the proposed solutions has been a separation of transport pathways either through differential usage of different FG nups types by different transport protein types, or by spatial segregation on the nanoscale [43,44,83,100,101,173,252,253,324,334]; other mechanisms, such as dynamical switching between export and import, have been proposed as well [281]. However, a consensus picture is still lacking, with a number of controversies and discrepancies arising from different experiments. We briefly summarize the current state of the art.

Using permeabilized cells, single-molecule tracking showed that the transport efficiency and the speed of translocation of the transport protein Importin- β increases with increasing its concentration [324]. This counter-intuitive finding is at odds with the predictions of minimal theoretical models based on the exclusion process theory [281]. It is in line, however, with in vitro experiments on colloids that were engineered to carry transport proteins on their surface. On planar assemblies of FG nups, the two-dimensional mobility of these colloids was strongly dependent on the presence of free transport proteins in solution: by competitive binding to the FG nups, these free transport proteins reduced the number of accessible binding sites for the colloids and therefore effectively reduced their binding to the FG nup assembly and thus increasing the mobility [172].

With respect to the effects of the different types of translocating molecules on each other, the evidence is also still controversial. The presence of the transport proteins has been shown to reinforce the permeability barrier created by the FG nups towards neutral cargoes [23,43,83], consistent with the theoretical notions of Section 4.1.2.1. In particular, ref. [43] showed that an increase in the concentration of Importin-β decreased the passive transport of GFP monomers, dimers and trimers; this effect could be significantly modulated by the presence or absence of RanGTP in accord with its function as a catalyst of transport protein unbinding from the FG nups. On the other hand, previous studies [252,253] showed that passive cargoes (dextrans) do not significantly affect the translocation of BSA-NLS cargo facilitated by transport proteins. Similarly, earlier work indicates that two different transport proteins (Importin-β and Transportin) interact with different domains of the nuclear basket FG nup Nup153 [335]. The results were interpreted as the “uncoupling” between the passive and facilitated modes of transport. The pathway separation hypothesis is also supported by super-resolution measurements of the trajectories and distributions of passive and facilitated transport pathways [44], but these results have been criticized on technical grounds [92,336].

Although the precise nanoscale picture of the NPC is still incomplete, it is clear that both FG nups and transport proteins (and potentially RanGTP) need to work together to achieve the unique transport properties that characterize the NPC. Further combination of experimental, theoretical and computational approaches is necessary. The progress in this area will have impact on the understanding of other non-equilibrium spatially inhomogeneous nanoscale systems, such as liquid droplets and other aggregates in the cell [159,160], as well as artificial composite nanomaterials [337,338].

4.3. Nucleo-cytoplasmic transport cycle as a pump

In the previous sections, we have focused on the biophysical characterization of the assemblies of the disordered proteins in the NPC, and on how their interactions with the transport proteins dictate the dynamics of translocation of protein-transport complexes through the NPC channel, and thus the transport efficiency and selectivity.

Although the translocation of transport proteins through the NPC is a key step in nucleo-cytoplasmic transport, it is only one component in the transport cycle. In its entirety, a complete transport cycle acts as an energy-driven pump that can generate import and export fluxes against concentration gradients, and maintain the system in a non-equilibrium steady state. In this section we discuss the current understanding of the biophysics, energetics and main principles of operation of the active cycle of the nucleo-cytoplasmic transport machinery.

Overall, the directionality of the transport cycle relies on the consumption of GTP and on the asymmetry in the nucleo-cytoplasmic partitioning of the protein Ran, with its RanGDP form being abundant in the cytoplasm and its RanGTP form being abundant in the nucleus. This asymmetric distribution of Ran relies on the asymmetric distribution of RanGAP and RanGEF, two factors responsible for GTP hydrolysis in the cytoplasm and GDP-to-GTP exchange in the nucleus, respectively [5,339]. The complete nucleo-cytoplasmic exchange cycle comprises three inter-linked loops, shown Figure 36. These loops are the import cycle, the export cycle, and the NTF2/Ran cycle that is responsible for recycling of RanGDP into the nucleus and for the maintenance of the RanGTP/GTP gradient.

Figure 36.

Full scheme of the nucleo-cytoplasmic transport pathways for Importin-β, including various adaptor molecules such as Importin- α, CAS and RanBP. For illustrative purposes, the various reactions are indicated by uni-directional arrows, corresponding to the “normal” operational cycle of the NPC. However, all these reactions are reversible, with the exception of the GTP hydrolysis, which is catalyzed by RanGAP in the cytoplasm and can be considered irreversible for all practical purposes. The irreversibility of GTP hydrolysis defines the directionality of the whole cycle, as indicated by the arrows in this figure. Reproduced from [339], permission pending.

The details of the import cycle and the Ran/NTF2 cycle are described in Section 2. The export cycle is similar to the import cycle, as shown in Figure 36. In the nucleus, export-specialized transport proteins (collectively known as Exportins) bind the export cargo through the Nuclear Export Sequence (NES), analogous to the NLS for import. However, unlike the import complexes, the export complexes also contain RanGTP bound to an Exportin. Upon translocation of the export complex to the cytoplasm, RanGTP is hydrolyzed by RanGAP, releasing the export cargo and the resulting RanGDP from the Exportin. It is crucial to emphasize that, with the exception of RanGTP hydrolysis, all the other reactions in the nucleo-cytoplasmic transport cycle are thermodynamically reversible [6,85,340]. It has also been shown that the accumulation gradient of certain cargoes can be reversed by reversing the gradient of RanGTP between the nucleus and the cytoplasm [341].

Figure 37 illustrates the generation of the non-equilibrium steady state concentration difference between the nucleus and the cytoplasm by the nucleo-cytoplasmic transport “pump”. Cargo with a nuclear localization sequence accumulates in the nucleus, but such accumulation does not occur in the absence of GTP and Ran.

Figure 37.

Energy dependence of Nuclear Import. In the absence of GTP and Ran, the cargo reaches the nuclear envelope but does not accumulate inside the nucleus. For comparison with normal import see Figure 31. Adapted from [78], permission pending.

Notably, viewed as an import machine, the NPC operational cycle is not very efficient. Experimentally measured ratios of nuclear and cytoplasmic concentrations of import cargoes are in the range of $\frac{C_n}{C_c}\simeq 10-30$ [85,86,340,342]. Under steady state conditions, this implies that translocation of one cargo molecule across the nuclear envelope translates into a free energy increase of approximately by Δμ = k_BT ln(C_n/C_c) ≃ 3 k_BT [90]. However, every translocation requires hydrolysis of one GTP molecule (or an additional GTP molecule for the re-export of the Importin-α adaptor), generating approximately 20 k_BT of energy [256], seven times more than required to transport one cargo against the typical concentration gradient. This makes NPC import rather inefficient compared with other bio-molecular machines, such as the sodium/potassium pump or the bacterial flagellar motor that can harness almost all of the energy gained by ATP/GTP hydrolysis towards the creation of a non-equilibrium concentration gradient or towards mechanical work [90,343]. These observations come with the caveat that most of these concentration estimates are based on measurements with artificial cargoes, such as GFP. These artificial cargoes do not have a function in the nucleus, (e.g., binding to the DNA), and may therefore remain free to leak back due to excess accumulation in the nucleus [85,344].

Given the low efficiency of the transport cycle, it is possible that the import-export system is simply hitch-hiking on the RanGTP/GDP de-mixing cycle, which has other important roles, such as nucleosome positioning during cell division [340,345], and therefore is not necessarily optimized to facilitate cargo de-mixing between the nucleus and the cytoplasm. This point of view, which defines the “futile cycle” [346] of RanGTP/RanGDP conversion as a primary driver of the nucleocytoplasmic transport cycle, has been useful in conceptualizing the principles of nucleocytoplasmic de-mixing using the methods of non-equilibrium thermodynamics [347].

In principle, all the reactions involved in the nucleocytoplasmic exchange can be computationally described with appropriate rate equations, but understanding of the full picture remains complicated due to the large number of various molecular complexes involved. Therefore, the predictions remain sensitive to the choice of parameters and assumptions, and are often at variance with each other, both on the computational and experimental fronts [86,87,340,342,344,347-350]. All these experimental and computational studies mostly agree that the initial accumulation of import cargo in the nucleus follows simple first order kinetics, and the initial accumulation rate/flux is linearly proportional to the cargo concentration in the cytoplasm. On the other hand, the various studies are less consistent about the saturation levels that are reached when the influx of the cargo is balanced by the outflux. [340,344,349,350]

Similar uncertainty remains on how the relative concentrations of cargo in nucleus and cytoplasm depend on the numbers of transport proteins, Ran, RanGAP/GEF and various other adapter proteins in the cell. Timney et al. [86] found that the nucleo-cytoplasmic concentration ratio increases with cytoplasmic concentration of the transport proteins, while Elbaum and coworkers predict a non-monotonic function of the transport protein concentration [347,350]. Finally, Riddick and Macara observed that the import rate is decreasing with the concentration of Importin-β (due to the depletion of RanGTP), although the connection between the initial accumulation rate and the relative concentrations at saturation is non-trivial [87,342]. It has also been shown that the competition of the transport proteins for different cargoes might be important [344,349,350]

It is likely that different behaviors are observed in various regimes depending on relative concentrations of individual components of the nucleocytoplasmic transport cycle. One can speculate that the wide range of observed behaviors might endow the NPC transport with additional flexibility, so that its function can be modulated in different conditions, such as different stages of the cell cycle.

5. Conclusions and Discussion

NPC is a vital biological machine that regulates transport and communication between the cell nucleus and the cytoplasm. The mechanism of its operation presents several physical puzzles, among them its ability to rapidly, and yet selectively, simultaneously translocate many macromolecules through a disordered, crowded and confined medium. Despite its enormous complexity, theoretical and experimental physics approaches have been crucial in elucidating the properties of NPC components, its internal spatial organization and the dynamics of transport. These physical approaches, combined with the increasingly detailed picture of its biochemical and structural aspects, have started to converge to unified physical principles of NPC organization and transport, some of which have been successfully recapitulated in artificial nanochannel mimics of the NPC. At the same time, these studies of the NPC have revealed and highlighted a rich set of underlying physical behaviors that connect the NPC research to a wide range of areas of physics, including collective polymer behavior in confinement, phase-separation in nano-confinement, specificity of multivalent interactions, and crowding effects in stochastic nano-scale transport.

Several main questions have captivated the attention of the field in the past decade, and have benefitted from physical approaches:

• What determines the ability of the NPC to combine high thermodynamic specificity/selectivity with high rapidity and throughput in the steady fluctuating and multi-species environment of the cell?

• What are the main biophysical properties of the intrinsically disordered components (FG nups) of the NPC?

• What is the spatial organization of the assembly of polymer-like FG nups within the NPC?

• How do the collective dynamics and multivalent interactions of the transported molecules and these intrinsically disordered heteropolymers answer the first question?

The intrinsically disordered proteins lining the NPC channel (known as FG nups) are the central component of the NPC transport mechanism. They serve a twofold role of 1) providing the target for the transport protein binding and shuttling through the NPC, and 2) providing a permeability barrier for the excluded cargoes. The exact biophysical properties of the FG nups and their assemblies have been a subject of intense controversy, in particular about the respective importance of polymer-chain entropy on the one hand, and cohesiveness or even gelation, on the other, in establishing the transport barrier. In the main, the research of the past decade has shown that the behavior of individual FG nups and their assemblies can be well understood in terms of physics of moderately cohesive polymers, and is well described by theoretical and computational models of varying degrees of coarse-graining. In particular, interactions between the FG nup chains often result in formation of condensed phases in vitro, whose morphology may be different in different geometries (bulk phases, surface grafted layers and nanochannels). This has been described in Sections 3.1-3.3. In actual NPCs, however, descriptions of the FG nup phase behavior will also need to take into account the presence of cargo-carrying transport proteins.

The second crucial feature of the NPC transport is the transient multivalent binding of these transport proteins to the FG nup assembly within the NPC, which plays a central role in the selectivity of the NPC transport. While one-to-one intermolecular affinities are weak among the FG nups themselves and between individual FG motifs and transport proteins, multivalency facilitates high thermodynamic partitioning of transport proteins into FG nup assemblies, thus creating the basis for strongly selective transport. Overall, the equilibrium permeability of the FG nup assembly towards the transport proteins arises from the balance between, on one hand, the free energy cost of insertion, which combines osmotic, entropic and steric effects, and, on the other hand, the free energy gain arising predominantly from the attractive interactions of the transport proteins with the FG nups. Thus, whereas larger inert molecules face a free energy barrier to cross FG nup assemblies of the NPC, transport proteins face one or more free energy wells across the NPC allowing their penetration and eventual translocation through the NPC. Minimal physical models have succeeded in semi-quantitatively replicated data from in vitro experimental assays of FG nup assemblies with transport proteins, including differences in the selective penetration by transport proteins and inert molecules. These topics have been covered in Sections 3.4-3.5. These, insights, obtained mostly from the studies of equilibrium or non-equilibrium steady state assemblies, potentially can be modified under conditions of direct energy input through GTP hydrolysis in the active cycle of the NPC.

In addition to the thermodynamics of transport protein partitioning into the NPC, kinetics of their translocation is another crucial factor in determining NPC selectivity, speed and throughput. At the molecular scale, the translocation of the multivalent transport proteins through the spatially inhomogeneous polymer assembly of FG nups within the NPC passageway is a complex process, which is still incompletely understood. However, multivalency of transport protein/FG nup interactions and the flexibility of the FG nups are likely to play important roles here as well. Their combination enables apparently strong thermodynamic binding and partitioning without inhibiting the lateral “millipede” (or “slide-and-exchange”) – like motion of the particle through the FG nup assembly that allows the transport proteins to rapidly translocate and exit from the NPC. These topics have been covered in Sections 4.1-4.2

Remarkably, much can be understood about the NPC transport mechanism even in the absence of a complete picture of the microscopic motion. The dynamics of particle translocation through the NPC can be viewed as a thermally activated diffusive transport in an effective free energy profile, determined, the interactions between the transport proteins and the FG nups, by the local density of the FG nups and their local cohesiveness. Transport proteins, experiencing an attractive effective potential profile, dwell longer within the NPC, increasing the likelihood of successful translocation events and increasing the total particle flux rate. This mechanism has been known in many contexts as “facilitated diffusion”.

Overall, the selectivity of the NPC (and other similar nanochannels) arises from the balance of two opposing effects: attractive interaction with the pore enhances the flux through the pore at moderate interaction strengths and low concentrations, while stronger interactions and higher concentrations can block the transport. Importantly, accumulation of the transport proteins in the pore can also impede the translocation of inert molecules, thus further enhancing the transport selectivity in the presence of non-specific competitors. Theoretical, computational and experimental models based on these ideas, implemented and studied through a variety of computational and experimental techniques, successfully capture the dynamics of transport in in vitro nanopore NPC mimics and other selective nanochannels. Remarkably, these ideas work well even for very large cargoes whose size approaches the inner diameter of the NPC channel.

The robust nature of the physical concepts underlying the principles of the NPC transport might also explain the robustness of its transport mechanism with respect to structural perturbations, as well as its high conservation among different species, despite substantial evolutionary divergence of its molecular components. On the other hand, the precise aspects of transport can be modulated via specific chemical modifications, such as glycosylation or phosphorylation of the FG nups, further enhancing its flexibility and adaptability to various cellular conditions.

While much of this review and much of biophysical research in the past decade has focused on the properties of FG nup assemblies and the thermally activated diffusion of the transport proteins through the NPC channel, it should be emphasized that the NPC is only a part of a more extensive nucleo-cytoplasmic transport cycle. This cycle operates as an active thermodynamic pump, powered by GTP hydrolysis and relying on the nucleo-cytoplasmic asymmetry in the distribution of certain enzymes. Only few studies have attempted to tackle this problem so far. Although in general it can be thought of as a very large chemical reaction network, we currently lack understanding on the coupling between the kinetics, energy consumption and the structural and dynamic properties of the NPC. Such understanding will be of paramount importance when considering the NPC in a wider biological and biomedical context and its function in various health and disease processes. This topic has been covered in Section 5.

The overall conceptual physical understanding has reached the stage that it can be applied to outstanding specific biological and biomedical problems such as involvement of the NPC in cancer, neurodegenerative diseases, gene regulation and device fabrication inspired by the NPC for selective sensing, sorting and transport of macromolecules. However, with the field converging to an overall consensus about how molecular properties and physical concepts translate into the functional behavior of the NPC, several open questions remain. A full quantitative understanding of how transport through the NPC is affected by various forms of crowding, caused by different types of cargo-bound and free transport proteins moving into and out of the nucleus cargoes, is still lacking. Another equally important subject that has yet received only minimal attention from the physics perspective is mRNA export - a crucially important topic from the biological and biomedical perspectives. Other effects such as the mechanics of potential conformational changes of the NPC structural scaffold during transport have also not been covered in this review [351,352]. These subjects are likely to be areas of exciting new discoveries in the future.

Finally, the quest for understanding NPC function has motivated and inspired a range of physical questions and models. Such models are now ready for further in-depth analysis of questions related to equilibrium and non-equilibrium thermodynamics and kinetics at the nano-scale. The NPC may thus provide a fruitful venue for understanding the coupling of nano-mechanics, fluctuations and chemical reactions.

Figure 14.

Multivalency of transport protein binding to FG nups. Top: Schematic illustration of the multivalent binding of a transport protein (Importin-β) to an FG nup (Nup153). In the classical picture the interaction predominantly arises from the binding of the hydrophobic side chains of the phenylalanines (shown in red rings) to the hydrophobic grooves on the transport protein (shown in blue). Bottom: schematic illustration of the multivalent binding-unbinding process Adapted from [216] and [119] , permission pending.

Figure 23.

Illustration of the “slide and exchange” mechanism; see text for details. Adapted from [134], permission pending.