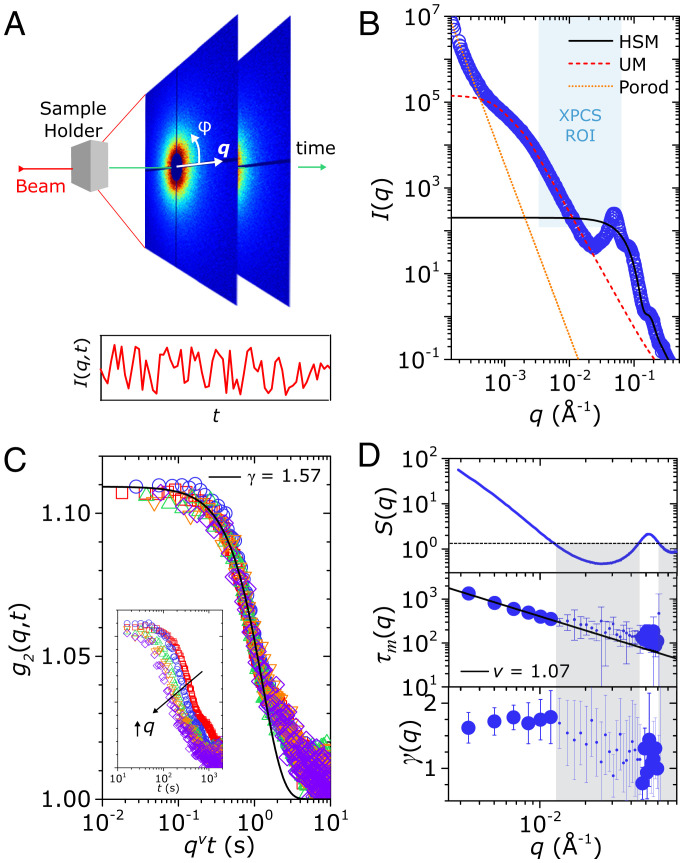
Fig. 2.

Microscopic dynamics of the arrested gel probed at quiescence via XPCS. (A) Illustration of the XPCS experimental setup. A partially coherent synchrotron X-ray beam strikes the sample, and scattered speckle intensity maps (with coordinates defined by the wave-vector q and azimuth angle $\phi$) are measured as a function of time. Correlations of the measured speckle intensity $I(q,t)$ are taken to obtain the second-order correlation function $g_2(q,t)$ as a function of delay time t. (B) USAXS intensities of the arrested gel. The scattering is captured by a hard sphere model (HSM) at high q, a unified model (UM) at intermediate q, and a Porod scattering response at low q. The region of interest probed by XPCS is shown by the shaded region, which is bound by q = 0.0032 Å⁻¹ and 0.063 Å⁻¹ and a noise floor at low $I(q)$. The UM captures the cluster size $\xi$ of the associative gel and shows that the XPCS region of interest is within the primary cluster size. All fitting parameters are listed in SI Appendix, Table S1. (C) The second-order correlation function $g_2(q,t)$ as a function of delay time $t$ for the arrested system in situ gelled in a capillary (see holder configuration in SI Appendix, Fig. S3). The correlation decay is fitted to the Siegert relation in Eq. 2. The $x$-axis is rescaled by $q^v$ with $v=1.07$; data collapse here indicates that superdiffusive dynamics drive both the fitted decay and the long-time tail. The inset shows the original q-dependent $g_2$ data in the range $0.0032{ \text{Å}}^{-1}\le q\le 0.010{ \text{Å}}^{-1}$ (increasing in q from right to left). (D) Graphs of the q-dependent structure factor $S(q)$, microscopic relaxation time ${\tau }_m(q)$, and compressing exponent $\gamma (q)$. The ${\tau }_m(q)$ and $\gamma (q)$ values shown are averages taken from 20 independent experiments conducted in the capillary (see statistics for $q=0.0032{ \text{Å}}^{-1}$ in SI Appendix, Fig. S5). The structure factor $S(q)$ is obtained by dividing $I(q)$ by the HSM results (Fig. 2B). The dashed line in the $S(q)$ plot indicates the noise threshold dictated by low $I\left(q\right)$; measurements made at $q$ corresponding to $S\left(q\right)<S{\left(q\right)}_{\mathit{Noise}}$ exhibit larger error bars, as shown. The data points in this noise floor are indicated by smaller symbols, and are shaded in gray. The relaxation times above this noise floor, ${\tau }_m(q)$ at $q\le 0.012{ \text{Å}}^{-1}$, are fitted to the relation ${\tau }_m\left(q\right)=C{q}^{-v}$ to obtain $v=1.07$.