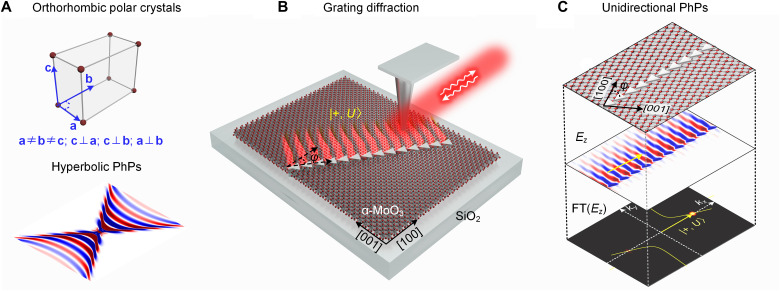
Fig. 1. Schematic of grating diffraction of unidirectional PhPs in high-symmetry orthorhombic crystals.

(A) The crystal structure and dipole launched hyperbolic PhPs (E_z electric field distribution) at the surface of (high symmetry) orthorhombic crystal α-MoO₃. (B) Schematic of unidirectional grating diffraction of PhPs via blazed grating in orthorhombic α-MoO₃. By changing the angle φ between the grating direction and α-MoO₃’s [100] crystal direction, it is possible to break the up-down mirror symmetry in diffraction [see FT(E_z) image in (C)], which enables the unidirectional diffraction of PhPs, as illustrated here for the ∣+ , U⟩ state. (C) Illustration of unidirectional PhPs. Upper layer: Top view of blazed grating and lattice of α-MoO₃; the blazed grating is oriented with an angle φ relative to α-MoO₃’s [100] crystal direction; middle layer: numerically simulated electric field distribution E_z of the grating-excited PhPs; bottom layer: Polaritonic isofrequency contours and Fourier Transform (FT) of the simulated E_z of PhPs (yielding the bright spots). The diffraction state is indicated as ∣+ , U⟩, where + indicates the direction of k (yellow arrow), and U marks the PhP diffraction on the up-side of the grating.