Figure - PMC

Skip to main content

An official website of the United States government

Here's how you know

Here's how you know

Official websites use .gov
A .gov website belongs to an official government organization in the United States.

Secure .gov websites use HTTPS
A lock ( ) or https:// means you've safely connected to the .gov website. Share sensitive information only on official, secure websites.

View full-text article in PMC

. 2022 Jun 16;38(15):3710–3716. doi: 10.1093/bioinformatics/btac395

Search in PMC
Search in PubMed
View in NLM Catalog
Add to search

© The Author(s) 2022. Published by Oxford University Press.

This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0/), which permits unrestricted reuse, distribution, and reproduction in any medium, provided the original work is properly cited.

PMC Copyright notice

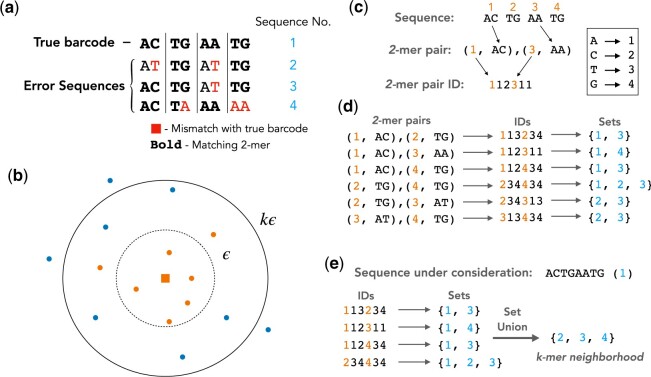
Fig. 1. — (a) Illustration of the pigeonhole principle for l = 8 and k = 2 (i.e. $p = l / k = 4$ ). Sequences 2 and 3 are within Hamming distance 2 of the true barcode. It follows from the pigeonhole principle that these error sequences share two or more 2-mers with the true barcode. Since Sequence 4 has Hamming distance 3 to the true barcode the pigeonhole principle only guarantees that it shares one 2-mer with it. Nevertheless, Sequence 4 still shares two 2-mers with the true barcode since two of its errors appear in the same 2-mer. (b) A given sequence (orange square) surrounded by its neighbors (dots) in sequence space. The orange dots are the k-mer neighbors of the given sequence, i.e. all sequences that share at least $p - ϵ k$ -mers with it. The blue dots are sequences not included in the k-mer neighborhood. The dashed circle is the ϵ-neighborhood of the sequence and the solid circle is the boundary for the k-mer neighbors, i.e. no k-mer neighbor appears outside the solid circle. Note that l is a multiple of k in this case and that all ϵ-neighbors of the sequence are also k-mer neighbors, this is guaranteed by the pigeonhole principle. (c) Illustration of how a pair of 2-mers are converted into a combination ID. First a pair of 2-mers is selected. Each 2-mer has a location in the sequence specified by the orange numbers. The 2-mer pair is then converted to an ID by assigning each of its nucleotides to a number specified by the conversion table on the right. (d) The k-mer Index for the set of sequences from the panel a, including only the 2-mer pairs shared by at least two sequences in the dataset. The blue numbers correspond to the sequence numbers specified in the panel a. Furthermore, the k-mer Index only includes the combination IDs with the corresponding sets and the 2-mer pairs (leftmost column) are only included here for illustrative purposes. (e) A schematic showing the process of finding the k-mer neighborhood of Sequence 1 from the panel a using the k-mer Index from the panel d. First all combination IDs of Sequence 1 are found and the corresponding sets are obtained from the k-mer Index. The set union of the sets yields the set of all sequences that share at least one combination ID with Sequence 1. By excluding Sequence 1 from this set we obtain its k-mer neighborhood (A color version of this figure appears in the online version of this article.)