Cryo-EM of Helical Polymers

Abstract

While the application of cryo-EM to helical polymers in biology has a long history, due to the huge number of helical macromolecular assemblies in viruses, bacteria, archaea and eukaryotes, the use of cryo-EM to study synthetic soft matter non-covalent polymers has been much more limited. This has mainly been due to the lack of familiarity with cryo-EM in the materials science and chemistry communities, in contrast to the fact that cryo-EM was developed as a biological technique. Nevertheless, the relatively few structures of self-assembled peptide nanotubes and ribbons solved at near-atomic resolution by cryo-EM have demonstrated that cryo-EM should be the method of choice for structural analysis of synthetic helical filaments. In addition, cryo-EM has also demonstrated that the self-assembly of soft matter polymers has enormous potential for polymorphism, something that may be obscured by techniques such as scattering and spectroscopy. These cryo-EM structures have revealed how far we currently are from being able to predict the structure of these polymers due to their chaotic self-assembly behavior.

1. Introduction

There has been a revolution in structural biology due to recent great advances in cryo-EM^1–3. We will not discuss in this brief review the impact of this revolution, and how cryo-EM has now become the method of choice for determining the atomic structure of macromolecular complexes. Rather, this review will be narrowly focused on introducing chemists and materials scientists to why cryo-EM should be the method of choice for determining the atomic structure of helical polymers formed from peptides and small molecules. But first, some introduction from structural biology is helpful.

It is probably fair to say that most protein (by mass) in both prokaryotic and eukaryotic cells is found in the form of helical polymers. In prokaryotes some well-known examples are the actin and tubulin homologs⁴ (e.g., MreB, ParM, FtsZ, etc.), flagellin and pili⁵. In flagellated bacteria, flagellin can be the single most abundant protein. In response to large amounts of DNA damage, the RecA protein, which forms a helical polymer on DNA, can be the single most abundant protein in bacterial cells⁶. In eukaryotes, in addition to actin (the single most abundant protein) and tubulin there are the intermediate filaments, collagen, etc., and we are still learning about other polymers within cells. For example, we now understand that nucleated-polymerization of the helical inflammasome initiates a pathway leading to pyroptosis⁷. The first virus ever isolated, tobacco mosaic virus (TMV), is a helical polymer of a protein bound to single-stranded RNA^8,9. The early structural characterization of viruses led to the realization that the two simplest ways that multiple copies of a single protein could be assembled into a capsid involved either a helix or an icosahedron^10,11. The frequently overlooked reason for the ubiquity of helical polymers in biology is that a helical assembly is the most likely consequence of any arbitrary favorable interaction between two copies of the same molecule when this interaction is extended to multiple subunits¹².

It is no coincidence, therefore, that the first application of three-dimensional reconstruction from electron microscopic images to a biological system was for the helical tail of an icosahedral bacteriophage¹³. While the resolution obtained from negatively stained samples in this pioneering work in 1968 was about 35 Å, it nevertheless opened up the possibility that two-dimensional EM images might be routinely used to generate three-dimensional reconstructions of biological assemblies. A simple measure of progress is that the same bacteriophage T4 tail tube has now been reconstructed at 3.4 Å resolution using cryo-EM¹⁴, which is an increase in information content by about 1,000 from the work done in 1968. In fact, this comparison illustrates the general progress in cryo-EM, where a near-atomic level of resolution has now become the standard, and not the exception. To put this in perspective, a search of the Electron Microscopy Data Bank shows 440 helical structures deposited with better than 5.0 Å resolution, and the number of such deposits per year¹⁵ shows the exponential growth reflecting the overall “Resolution Revolution” in the field^1,3,16.

In addition to their ubiquity, helical polymers have the attractive feature that, in principle, a single helical polymer provides all the information in a single projection image to reconstruct in three-dimensions. This is due to the fact that the helical symmetry is generating what is effectively a single-axis tilt series showing all of the different projections of a single subunit as it is rotated about the helical axis. One thus has no need for other views, such as down the helical axis, in the same way that medical tomography of an asymmetric volume (e.g., a skull or a chest) can obtain all the needed three-dimensional information from collecting the projections as a source and detector are rotated around a single axis. In practice, the high degree of noise present in cryo-EM images (with a signal-to-noise ratio <<1) due to electron shot statistics, resulting from the low dose needed to minimize radiation damage, requires that extensive averaging must be used, so one may need to collect images from hundreds or thousands of polymers to reach a near-atomic level of resolution. Further, the idealization that a single projection contains all of the information needed may only be true in the absence of what is called in Fourier space “Bessel-overlap” which may arise at relatively low resolution when there are a limited number of subunits in a true repeat. Thus, if one has a helix with exactly seven subunits per turn, then a projection image of a single filament will only show seven different projection angles for the component subunit. This would be equivalent to a single-axis tilt series with tilt increments of 51.4°, yielding a very low resolution reconstruction. For example, if the filament had a diameter of 100 Å, then the resolution obtainable would only be ~ 90 Å, using the relationship that d = DΔα, where d is the resolution, D is the diameter, and Δα is the tilt increment in radians. Since there is no reason why any polymer, outside of a crystal, should have an integer number of subunits per turn¹⁷, consider a filament with 7.1 subunits per turn. A single filament would generate 71 different projections of the component subunit, equivalent to a single-axis tilt series with 5.07° increments. For the 100 Å diameter filament, the resolution obtainable would be 8.8 Å, still quite far from what is needed for building atomic models. We expect that filaments will have a random azimuthal orientation in cryo-EM images, so multiple filaments can thus be used to finely sample the azimuthal orientation space, yielding the information needed for high resolution.

It is helpful whenever discussing helical polymers to introduce the “helical net” (Fig. 1) and some terminology essential for describing the symmetry. Helical symmetry, or screw symmetry, involves a coupled rotation (∆θ) about a helical axis with a translation (∆z) along the helical axis. In addition, there can be a C_n rotational point group symmetry about the helical axis. In the absence of a rotational symmetry, any helical lattice can therefore be completely described by the parameters of the 1-start helix that passes through every subunit, where the pitch of the 1-start helix is Δz*360°/∆θ. The “start” number of the helix is simply how many times a horizontal line in the helical net intersects the helical lines (Fig. 1b,d).

Figure 1).

Helical symmetry is best understood in terms of the helical net.

(a) An illustration of a helix without point group symmetry (rise: 4 Å, twist: 55°, C₁). The asymmetric units (ASU) are represented by spheres. The right-handed 1-start helix that passes through every subunit is shown as a dashed line.

(b) The helical net of a, using the convention that the surface is unrolled and we are viewing it from the outside. The helix crosses the horizontal red line once, so the helix is called a 1-start. The helical rise and helical twist along the right-handed 1-start helix are labeled.

(c) An illustration of a helix with point group symmetry (rise: 4 Å, twist: 55°, C₅). Because of the rotational point group symmetry, any rotation of this structure by multiples of 72° is an identity operation. The asymmetric units are represented by spheres. The subunits along a single 5-start strand are shown in red, and the dashed lines show the 5-start helices.

(d) The helical net of c, using the convention above. The right-handed 5-start helices cross the horizontal red line five times, hence the name 5-start.

In a three-dimensional crystal the only allowed helical symmetries have 2, 3, 4 or 6 subunits per turn. But outside of a crystal there is absolutely no reason why the number of subunits per turn (360°/∆θ) should be integer. Formalisms that are based upon describing helical symmetry as integer ratios¹⁸ have a helical repeat, where one subunit can be translated along the helical axis by this repeat and be exactly superimposed upon another subunit. But such formalisms are ill-conditioned due to the fact that infinitesimally small changes in the helical twist result in huge changes in the helical repeat¹⁷, and it is much better to simply describe the symmetry in terms of the two continuously variable real numbers, Δθ and Δz. When there is a rotational point group symmetry present, there cannot be a 1-start helix that passes through every subunit. For a C_n point group symmetry, there will only be n-start helices and multiples of n. For example, if there is a C₅ rotational symmetry (Fig. 1), then the structure will only have 5-start, 10-start, 15-start, etc. helices. The convention that exists is that right-handed helices are generated by a positive rotation, while left-handed helices result from a negative rotation. The original convention¹⁸ for the helical net involved unrolling the surface of a cylinder and looking at this two-dimensional lattice from the inside of the cylinder, and this convention was used in much of the earlier literature. Since we actually look at most helical structures, whether using three-dimensional reconstruction, AFM, metal-shadowing, or SEM, from the outside, it makes more sense to reverse the original convention (Fig. 1b,d).

In addition to a point group rotational symmetry, there can be a dihedral symmetry such that the polymer has a 2-fold axis perpendicular to the helical axis. For polymers built from intrinsically asymmetric subunits such as peptides or proteins, this requires that the asymmetric unit in the polymer must be at least a dimer. When such a 2-fold symmetry exists along with an n-fold rotational symmetry, this can be represented as an overall D_n dihedral symmetry.

For over 30 years since the introduction of three-dimensional electron microscopy¹³ in 1968 the main approach used for the reconstruction of helical polymers was the Fourier-Bessel method¹⁸. An alternative approach, called the Iterative Helical Real Space Reconstruction (IHRSR) method¹⁹ has now dominated the field. A number of reviews have discussed the advantages of the IHRSR method and the limitations of the Fourier-Bessel approach^17,20–22. Since no one is currently promoting Fourier-Bessel methods as superior to real-space approaches, discussing this further is unnecessary. However, an early misconception was that one of the advantages of the real-space approach was that one did not need to understand Fourier-Bessel analysis. This, as discussed below, turns out to be wrong, and the greatest challenge in applications of IHRSR is usually determining the helical symmetry^15,23 which is best done through an understanding of the Fourier-Bessel formalism.

While all of the early applications of IHRSR were made with what is now legacy software, the SPIDER package^24,25, the IHRSR algorithm has been implemented in comprehensive modern packages such as Relion²⁶ and cryoSPARC^27,28.

2. Soft Matter

There is a vast literature and associated prodigious research effort on supramolecular assemblies of nanotubes from peptides and small molecules²⁹, but there have been only a handful of high-resolution cryo-EM structures from these complexes which we will discuss. One of the reasons that three-dimensional EM arose in the biological sciences as opposed to such areas as materials science or metallurgy (both areas where EM has also been extensively used) is that most biological specimens can be viewed as weakly scattering in terms of interactions with electrons having an energy of 100–300 kV. Thus, an electron passing through the sample will either not interact at all, or have a single interaction. In contrast, for a strongly scattering material such as a metal, an electron will typically have multiple interactions with the sample before it reaches the detector. This multiple scattering (or dynamic scattering) means that the image that is obtained can be quite complex and not simply related to the sample being examined. However, in cryo-EM of most macromolecular complexes it is reasonable to assume that the image, ignoring for the moment the Contrast Transfer Function (CTF), corresponds to the projected density of the sample. This relatively simple relationship leads to the ability to go from two-dimensional images to true atomic resolution volumes^30,31 using techniques such as weighted back-projection, algebraic reconstruction or Fourier methods.

Perhaps as a consequence of this history, the current capabilities of cryo-EM to routinely reach a near-atomic level of resolution for protein polymers are still largely unknown in materials science and chemistry. For example, there has been a mistaken belief that the “microbial nanowires” conducting electrons away from bacteria such as Geobacter sulfurreducens are Type IV pili, when it has now been shown by cryo-EM at near-atomic resolution that these filaments are actually a polymer of cytochromes³². Prior to the cytochrome publication, a 2017 paper in a chemistry journal stated that determining the actual structure of these filaments remains challenging due to the “low-resolution of electron microscopy techniques”³³. There have now been a number of published high resolution cryo-EM structures of synthetic polymers formed from peptides^34–38 that should begin to change this perception about resolution in chemistry and materials science, and we will focus on these papers in this review.

As shown in Fig. 2, when one reaches a resolution of ~ 4 Å there is no ambiguity in building atomic models into these peptide maps. The determination of the absolute hand can still be challenging, however. Since cryo-EM images are projections, information about the hand is lost, as a structure and the mirror-image of the structure will both give rise to indistinguishable projections. This can be understood at the anatomical level, where an x-ray of a left hand with the palm up is the same as the x-ray of a right hand with the palm down (Fig. 3). If one knew whether the palm was up or down, one could distinguish which was which. But in the absence of that knowledge there would be an enantiomorphic ambiguity.

Figure 2).

Cryo-EM has become the method of choice for helical polymers.

Cryo-EM maps better than 4 Å resolution, now routinely attainable, clearly resolve some side chains of the peptide or peptide-like compounds, and one has the ability to build atomic models de novo.

(a) Cryo-EM reconstruction of a cross-α nanotube at 3.8 Å resolution³⁸. The α-helices form stacks, and the three stacks forming the tube are each shown in a different color. The ASU is a single α-helical peptide containing 36 residues. The density from a single subunit is shown on the right as a grey mesh, and a ribbon diagram of the atomic model has been fit into this density.

(b) Cryo-EM reconstruction of a cross-β nanotube at 3.5 Å resolution³⁷. The β-sheets on the inside (yellow) are parallel, and those on the outside (cyan) are antiparallel. The ASU contains four peptides, shown on the right, forming four β-strands. Although each 8-residue peptide is chemically identical, each of the four peptides in the ASU is in a different environment.

Figure 3).

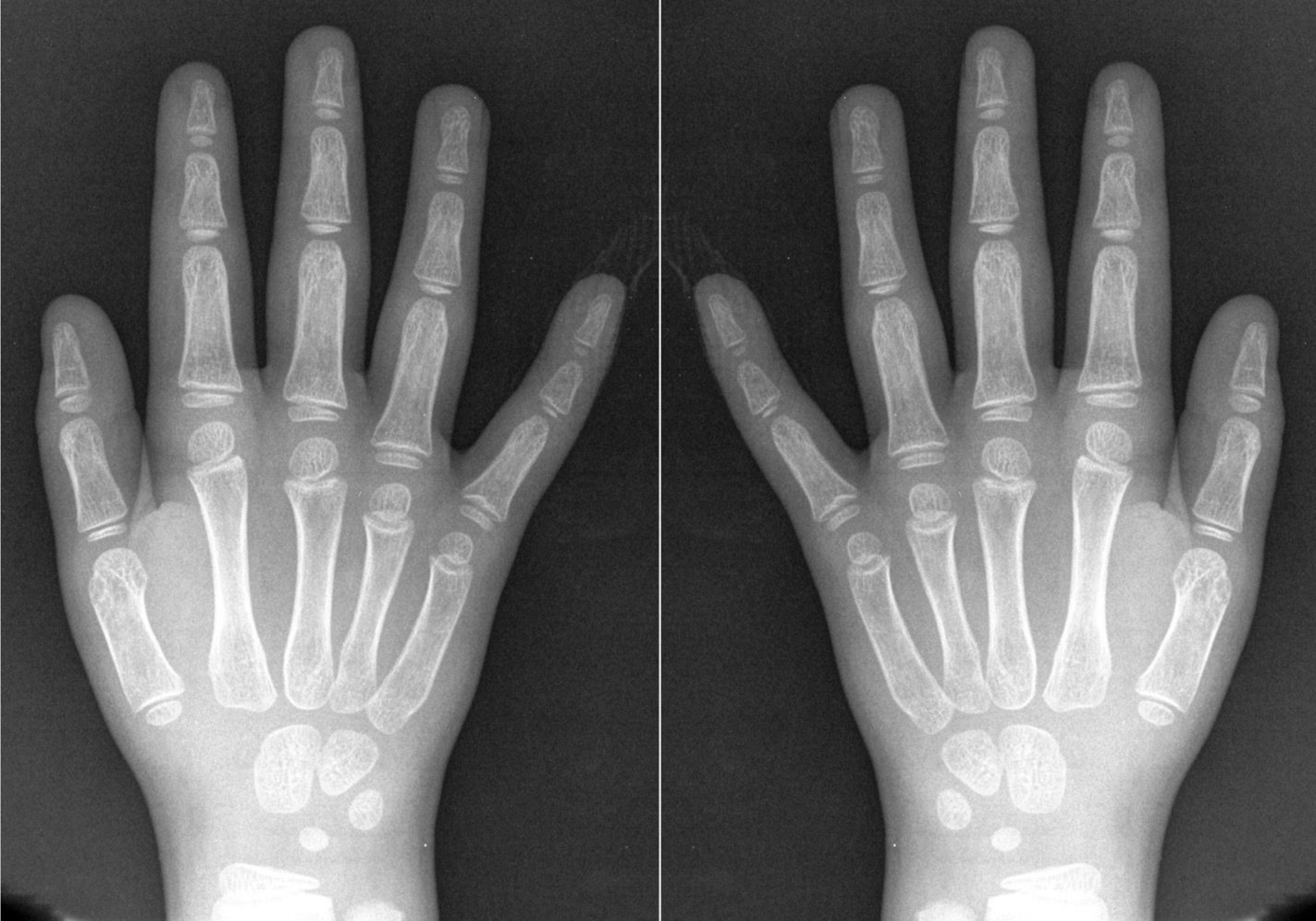
The loss of information about the absolute hand in projection images is best illustrated with a clinical x-ray of the human hand, since such x-ray images, like cryo-EM images, are projections. From a radiograph on the left, one cannot tell whether this is a right hand, palm down, or a left hand, palm up. The image on the right is simply the mirror image of the one on the left, and this could be either a left hand, palm down, or a right hand, palm up. Radiograph courtesy of Department of Radiology, University of California San Diego.

In cryo-EM, reconstructing a left-handed helix assuming that it is right-handed, or the opposite, should just generate a reconstructed volume that is the perfect mirror image of the true structure. One only needs to mirror this volume to correct this. A cryo-EM paper³⁹ looking at the assembly of amyloid filaments formed by a 101-residue fragment of a protein argued that the correct hand could be determined directly since the reconstructed volume using a twist of −7.68° had a better resolution than one generated with a twist of 7.68°. This result cannot possibly be true, since the projections of a right-handed volume will be indistinguishable from the projections of a mirror-image of this volume (Fig. 3). Therefore, the most likely explanation for their different resolutions involved the starting models for the left- and right-handed reconstructions. For example, one might have started both reconstructions with a volume having a left-handed twist, and it is therefore not surprising that the reconstruction with the left-handed twist had a better resolution. Right-handed versus left-handed versions of chiral monomers must necessarily be non-identical, just as a right-handed α-helix composed of L-amino acids must be different from a left-handed α-helix composed of D-amino acids (never found in nature). But the projections of a right-handed α-helix composed of L-amino acids would be indistinguishable from the projections of a left-handed α-helix composed of D-amino acids. A clever approach to see what such true enantiomorphs would look like was done by mirroring the entire PDB to create a library of 2.8M D-peptides⁴⁰. These could then be used to create D-analogs of a given peptide, which would resist proteases and could be used pharmacologically.

For natural proteins or synthetic peptides built from L-amino acids, one can thus establish the absolute hand of a reconstruction if the structure of the protomer contains a single α-helix, knowing that this must be right-handed. But β-sheets are more problematic, starting with the problem that one needs to consider whether the twist of a strand is being specified (typically right-handed) or the twist of the sheet (typically left-handed) is being described^41,42. In any case, while most proteins contain left-handed sheets composed of strands with a right-handed twist, an analysis of the PDB shows the presence of some left-handed twist strands⁴³, so the overall twist of the sheet will not be 100% reliable in assigning the correct hand to a reconstruction. For one amyloid-forming protein, atomic force microscopy (AFM) imaging revealed the presence of both left- and right-handed fibrils³⁹. AFM has also been used to detect helical hand and heterogeneity in other amyloid cross-β filaments^44,45. We have found that if the resolution of a reconstruction is 3 Å or better and β-sheets are present, then the pattern of backbone hydrogen bonds in the atomic model built into the map can be used to distinguish between the two hands. For the correct hand the hydrogen bonds look reasonable, while for the wrong hand the stereochemistry is quite flawed.

In general when α-helices are not present, or when β-sheets are present but the resolution is worse than ~ 3 Å, determining the absolute hand may be quite problematic, and one may need to use other techniques such as AFM or cryo-electron tomography to establish the hand. However, the simplest applications of both of these techniques are fairly low resolution, and for relatively thin and smooth nanotubes the helical hand may not be easily seen. AFM image analysis⁴⁶ and sub-tomogram averaging⁴⁷ may need to be employed in these cases. A study of chirality in nanofibers self-assembled from short amphiphilic peptides used TEM, scanning electron microscopy (SEM), AFM, molecular dynamics simulations (MD) and circular dichroism spectroscopy (CD)⁴⁸. The hand was quite clear from AFM for some of the fibril forms (but not for the thinnest ones), but it did not appear clear from SEM for any of the fibers. Since the TEM images were from negative stain, they (like cryo-EM images) will not show the hand⁴⁹. The CD signals appeared to be determined by the chirality of isoleucine residues, and thus have limited generalizability to other peptide assemblies either in terms of molecular chirality or supramolecular handedness. While we discuss below how symmetry determination may be a very challenging problem when reconstructing polymers, the determination of the absolute hand may actually be more challenging in some cases in the absence of α-helices, as is certainly the case for most synthetic soft matter nanotubes. A very recent paper on helical polymers formed from the octapeptide Lanreotide was able to show at 2.5 Å resolution that a C_β carbonyl fit much better into one map than the mirrored map⁵⁰, establishing the correct hand. Another approach possible at high, but less than atomic resolution, involves the curvature of the Ewald sphere, which can be used to determine the absolute hand⁵¹. This has been applied to large icosahedral viruses⁵², but is unlikely to be very useful for thin filaments at 3 Å resolution or worse. Nevertheless, in the absence of true atomic resolution (~ 1.3 Å or better), directly visualizing the chirality of molecules may still be possible.

There have been other applications of cryo-EM to look at designed protein polymers^53–57 (as opposed to naturally occurring ones), but almost all were at very limited resolutions with likely questions about whether the correct symmetry had been found¹⁵. The more recent one from Baker and colleagues⁵⁵ was done at a near-atomic level of resolution, generating confidence that the symmetry was correct.

3. Polymorphism

Most naturally occurring biological polymers, such as actin filaments, microtubules, TMV, etc. exist with a defined symmetry, although filaments such as actin^58,59 and amyloid⁶⁰ can have a large variability in twist about that defined symmetry. The single-particle approach in cryo-EM which is now being used to reconstruct helical polymers¹⁹ can surmount many of the problems caused by such heterogeneity since long-range order is not required for three-dimensional reconstruction. While the variable twist of an amyloid filament may mean there is no highly regular periodicity of features such as that generated by the cross-overs of two strands coiling about each other, by using short segments for analysis the local order that exists is still captured. The shorter the segment used, the less one is affected by the cumulative disorder. However, the shorter the segment, the less ability one has to align it with other segments given the extremely poor signal-to-noise ratios in cryo-EM images. There is thus a trade-off with using shorter segments, and the optimal length of a segment may change with every sample. Ultimately, however, one of the main limitations on resolution when working with helical filaments is this internal structural heterogeneity.

But heterogeneity of the helical symmetry itself is quite possible and frequently observed. When microtubules are polymerized in vitro they can have a large variability in the number of protofilaments⁶¹, with the number of protofilaments varying within the same microtubule. Similarly, amyloid filaments polymerized in vitro have been shown to be highly polymorphic⁶² and have raised questions about the validity of these in vitro polymers for understanding specific neurodegenerative diseases. When one works with the in vitro self-assembly of synthetic peptides, the potential for polymorphism is huge. A recent paper on the assembly of an octapeptide³⁷ showed that tubes could form with either four or five protofilaments, in addition to ribbons corresponding to a single protofilament (Fig. 4a,b). Within the context of designed peptide assemblies, this relatively limited degree of polymorphism can actually be seen as relatively well-behaved.

Figure 4).

Polymorphism is the norm rather than the exception with many peptide assemblies, and cryo-EM can sort out heterogeneity of polymers.

(a) & (c), representative cryo-EMs of KFE8 nanotube³⁷ (a) and 1-KMe₃ nanotube³⁴ (c). Scale bar is 50 nm.

(b) & (d), After automatic particle picking and reference-free 2D classfications, helical polymers are grouped into different classes. The differences are obvious by looking at the averages, and helical symmetry determination and high-resolution reconstructions can subsequently be done for each class. In (b) class 1 corresponds to tubes with five sheets, class 2 corresponds to tubes formed from four sheets, and class 3 is a ribbon containing a single sheet. In (d), class 1 corresponds to a filament with seven peptides per plane, and class 2 corresponds to a filament with six peptides per plane.

The potential polymorphism often manifests itself as different filamentous morphologies present within a sample that correspond to different helical symmetries (Fig. 4). However, it is also observed that closely-related peptides can form nanotubes with similar morphologies, but different symmetries. Despite the fact that the symmetry is different, the interfaces between protomers has been found to be well conserved (Fig. 5). Of course, to show this one must first determine the helical symmetry for each class of filaments. A similar phenomenon was also observed with proteins: for example, when green fluorescent protein (GFP) tags were added to pyrin domains (PYDs), the PYDs assembled into helical polymers with a different helical symmetry from those formed without the tags, but the local environment for the PYDs was quite conserved between both filament forms⁶³.

Figure 5).

Helical polymers made from small subunits can easily adopt different helical symmetries while maintaining relatively conserved interactions. Two peptide examples are shown here: (a)-(d) nanotube 29–20-2 compared with AS2; (e)-(h) nanotube Form I compared with F1-N2.

(a) & (e), The amino acid sequences of the peptides. The dots between the sequences indicate the residues that are non-identical in each of the pairs.

(b) & (f), The determined helical symmetry and atomic models of the nanotubes (PDB 7RX4 for AS2 and 7RX5 for F1-N2).

(c) & (g), The interface comparison between two nanotubes shows that relatively conserved contacts are maintained, even though the helical symmetry has changed.

(d) & (h), The averaged power spectrum (only showing one of two, as they look similar) of the nanotubes, and the helical indexing.

4. Symmetry Determination

One of the greatest challenges in reconstructing helical polymers, whether they are native biological assemblies or synthetic in vitro constructs, is determining the correct helical symmetry^{15,20–23,64}. We now understand that there is no simple metric that allows one to decide whether they have chosen the correct symmetry. For example, it would be nice to be able to say that if the resolution as determined by the FSC (Fourier Shell Correlation) reaches 4.0 Å or better, then one knows that they have the correct symmetry. But this is not the case, and we have seen many examples where the FSC is 4.0 Å or better but the map is uninterpretable, a consequence of using the wrong symmetry. We show (Fig. 6) how four different helical symmetries (only one of which is correct) generate “gold standard” FSC values that are all virtually identical (~ 3.5 Å). This gets to one of the problems with the use of the FSC, as it is not really a measure of true resolution but rather a measure of reproducibility. This is discussed in some detail in an earlier review⁶⁵ so we will not dwell on this here. But what becomes obvious is that if the wrong symmetry is imposed, reproducible “detail” can be present at seemingly high resolution that is actually a complete artifact. One can also show that the wrong symmetry will generate a reasonable map in some cases, but the resolution is limited. For example, a reconstruction of a bacterial conjugation pilus reached 5.0 Å using the wrong symmetry⁶⁶. However, with the correct symmetry the resolution obtained was 3.9 Å. A comparison of the two maps at 5.0 Å resolution showed that they were extremely similar, so if higher resolution had not been reached one would have been unable to decide which was the correct symmetry. How is this ambiguity possible? A comparison of the two helical nets⁶⁶ shows that the local packing for these two different symmetries are not that different. Thus, one can align images locally using the incorrect symmetry without doing too much damage to the resolution. However, the further one is from the center of the image the greater the mismatch will be between the actual symmetry and the incorrectly assumed symmetry, which is ultimately what is limiting the resolution. There are some helical structures where one might never reach high resolution due to disorder, heterogeneity, etc., and one thus must be concerned in these cases that the correct symmetry cannot be established with high confidence. What the mating pilus example illustrates is that one must explore all possible choices of symmetry before concluding that the correct one has been found.

Figure 6).

Ambiguities frequently exist in helical symmetry determination.

(a), The averaged power spectrum of nanotube F1-N2, and four possible helical symmetries generated from indexing the power spectrum.

(b), The “gold-standard” FSCs after applying those four different symmetries in helical reconstructions are nearly indistinguishable, despite the fact that three of these symmetries are wrong.

(c)-(e), The reconstruction volumes for those four different symmetries filtered to resolutions of 8 Å (c), 5 Å (d), and 3.5 Å (e). At 5 Å resolution or worse all four symmetries generate maps that might be considered reasonable for α-helical subunits.

(f), The density of a single helix is shown from the 3.5 Å map. The comparison between the density and the atomic model shows that symmetry 3 is the correct one.

(g), The model:map FSC for those four maps with different symmetries and corresponding atomic models. The commonly used arbitrary cutoffs (0.5 and 0.38) are shown. Using the FSC=0.38 criterion (where 0.38 =√ 0.143), only one of these (symmetry 1) might be excluded as obviously incorrect.

So how does one go about determining possible symmetries? The best approach involves starting with an averaged power spectrum from the images (Fig. 5d,h; Fig. 6a). Understanding and interpreting the power spectrum does involve the Fourier-Bessel formalism^18,67, and there are a number of reviews where this formalism is explained^21,68. It should be pointed out that the averaged power spectrum is different from the power spectrum of an averaged image. The averaged power spectrum is an incoherent average that is invariant under the shifts of images that are needed to generate a coherent real-space average. But the process of generating a coherent real-space average can introduce artifacts. For example, if one averages together images using a picture of Albert Einstein as a template, then the average will look like Einstein⁶⁹, and the power spectrum of this average will look like the power spectrum of Einstein. However, the averaged power spectrum will show no such artifact, and will actually represent the information in the raw images. Similarly, an average may be based upon the alignment of one very strong feature (such as a long-pitch helix), but other helices in the image are blurred out. The power spectrum of the averaged image will then only show this long-pitch helix, while an averaged power spectrum from the raw images will show features arising from all of the helices.

In rare cases, the averaged power spectrum, combined with a knowledge about the diameter of the filaments^21,22,70, may lead to an unambiguous determination of the helical symmetry. In the more likely case, there will be ambiguities. For example, a helical virus had at least 10 possible symmetries⁷¹, while 1-KMe₃ nanotube had > 30 possible symmetries³⁴. What can be seen in Fig. 6b is that metrics, such as the putative resolution determined by the FSC, may not correctly distinguish the correct symmetry from the incorrect one. Using atomic models built into the maps, one can only exclude one of the symmetries based upon a poor map:model FSC (Fig. 6g). But in this test, one first must build an atomic model into the map. These problems make fully automated searches impossible at the moment, and one still needs the active involvement of an observer who knows what a protein or peptide map should look like at different resolutions.

5. Chaos

The mathematician and meteorologist Edward Lorenz is widely quoted as having described chaos in the temporal evolution of a system thusly: “When the present determines the future, but the approximate present does not approximately determine the future.” Chaotic systems are therefore those that are incredibly sensitive to small changes. We have suggested that many peptide assemblies behave in such a chaotic manner, as small changes in sequence or assembly conditions can generate huge changes in the structures that are formed³⁷. A very striking example of this involves a 29-residue α-helical peptide that self-assembles into helical nanotubes³⁶. The semi-conservative mutation of a single arginine to a lysine resulted in: 1) tubes having approximately twice the diameter; 2) the asymmetric unit changing from a single peptide to two peptides, where the two peptides were now in different environments from each other; 3) the structure changing from four stacks of helices to three stacks. While these changes are not mystical or due to supernatural forces, they reflect quaternary interactions that are far beyond our current abilities to predict. In biology, chaotic assembly would be typically pathological (such as amyloid) and we expect that there has been intense selection against it over billions of years. Sickle cell disease is an interesting exception. Mutation of a single residue on the surface of hemoglobin leads to the aberrant polymerization of what would otherwise be a compact tetramer into a pathological fiber. But since people carrying the sickle cell allele have greater resistance to malaria, which has been the main factor in early mortality in many parts of the world for thousands of years, this allele has remained in human populations⁷².

Similarly, while it is known that pH can determine whether a peptide forms parallel or antiparallel β-sheets⁷³, and that certain peptide sequences will lead to parallel β-sheets while other sequences will lead to antiparallel sheets⁷⁴, we have shown that the same peptide will assemble into parallel sheets on the inside of a nanotube and antiparallel sheets on the outside of the same tube³⁷. We have called this an instance of “deterministic chaos” and it is yet another example of how the quaternary interactions defy predictability with current knowledge and tools.

6. Conclusion

The prior discussion highlights the challenges associated with cryo-EM analysis of helical polymers at near-atomic resolution. However, in order to gain perspective, it is instructive to look back ten years to gauge progress. At that point in time, direct electron detection cameras for electron microscopes were still being developed and were not widely available. These cameras enabled image capture at high detective quantum efficiency, with a vastly improved signal-to-noise ratio, and rapid acquisition times. This development was a necessary prerequisite for the “Resolution Revolution” in cryo-EM. Previously, few structures of biologically derived helical filaments and no structures of designed filaments had been solved to near-atomic resolution using cryo-EM helical reconstruction. The ensuing decade has led to an exponential growth in the number of reported high-resolution structures, but it is clear that the growth curve is still at a very early stage. Currently, high quality cryo-EM data sets can be routinely obtained for synthetic soft materials. The availability of these data sets now allows researchers to address the more challenging technical aspects of cryo-EM analysis, including determination of more effective methods to assign helical hand and determine helical symmetry. These efforts should result in greater numbers of near-atomic resolution structures of synthetic helical filaments. This structural information should facilitate research efforts aimed at the development of methods for reproducible and predictable de novo design of self-assembling soft materials. In the short term, research will continue to focus on assemblies derived from sequence-specific chiral oligomers, especially peptide and peptido-mimetic protomers. These substrates have the advantage that sequence-structure correlations have been established that can serve as the input for molecular design efforts. In addition, a huge number of non-peptidic soft matter nanotubes have been designed for many applications, such as optoelectronic materials^75–77. Very little structural information is available at high resolution for these types of assemblies, but it is clear that this information is critical for understanding the structural features that underlie their technological application and will be critical for materials informatics approaches to optimize function.

Biography

Fengbin Wang

Fengbin “Jerry” Wang completed his B.Sc. (2010) in Biosciences at Fudan University in Shanghai, China. After that, he started as a Ph.D. student in biochemistry at the University of Wisconsin-Madison under the supervision of Prof. George Phillips, Jr. Later, he re-located with his mentor and received his Ph.D. (2016) from Rice University. In 2016 he joined the research group of Prof. Edward Egelman as a postdoc, working on cryo-EM of microbial appendages and EM-based design of self-assembling nanotubes. In 2021, he received a prestigious NIH K99/R00 Pathway to Independence Award and will soon be launching an independent academic career.

Ordy Manuela Gnewou

Ordy Gnewou completed her B.A. in Chemistry (2018) at Lehman College-CUNY and is currently a Chemistry Ph.D. candidate at Emory University, where she works with Prof. Vincent Conticello. As an undergraduate, she worked in the lab of Dr. Donna McGregor where she performed synthesis and characterization studies of Rhenium tripeptide complexes for chemotherapeutic applications. In the Conticello lab, she currently investigates de novo design and structural analysis of peptides for the construction of synthetic helical assemblies for various applications.

Armin Solemanifar

Armin completed his B.Sc. degree in Polymer Engineering (2013) at Amirkabir University in Tehran, Iran. He continued his studies in the same field and received his M.Sc. degree in Polymer Materials Science and Engineering (2014) at University of Manchester, UK. He completed his Ph.D. (2021) at University of Queensland, Australia, under the supervision of Prof. Bronwyn Laycock working on understanding underlying mechanisms of electron transfer in microbial nanowires and improving electrical conductivity of peptide nanowires. During his Ph.D., he joined Prof. Vincent Conticello’s lab as a visiting research scholar and worked under his supervision on design, synthesis, assembly, and characterization of structurally defined helical peptide nanotubes. His research interests focus on peptide structure analysis and characterization of their electrical conductivity properties.

Vincent P. Conticello

Vincent Conticello is a materials chemist whose research focuses on the design and structural analysis of peptide and protein assemblies. Vincent was born in Delaware and graduated with a B.S. in Chemistry from the University of Delaware (1985). He completed his Ph.D. degree (1990) in Chemistry at Northwestern University under the direction of Prof. Tobin Marks. After performing postdoctoral research in Chemistry at Caltech and Polymer Science at the University of Massachusetts, Vincent joined the Department of Chemistry at Emory University (1995) as an assistant professor and is currently Professor of Chemistry.

Edward H. Egelman

Edward Egelman is a biophysicist known for his work on the structure and function of protein and nucleoprotein polymers. He developed the algorithm that is now widely used in cryo-electron microscopy for the three-dimensional reconstruction of helical filaments and tubes. His research has ranged from studies of actin to bacterial pili to viruses that infect hosts living in nearly boiling acid. Egelman was born in New York and graduated from Brandeis University in 1976 with a B.A. in physics. He started as a Ph.D. student in experimental high energy physics at Harvard, but changed fields and received his Ph.D. from Brandeis University in 1982 in biophysics. He was a Jane Coffin Childs postdoctoral fellow at the Medical Research Council Laboratory of Molecular Biology in Cambridge, UK, and became an Assistant Professor at Yale University in 1984. In 1989 he moved to the University of Minnesota where he was an Associate and Full Professor, and in 1999 moved to the University of Virginia where he is now a Harrison Distinguished Professor. He has been president of the Biophysical Society and Editor-in-Chief of Biophysical Journal, and is a Fellow of both the Biophysical Society and the American Academy of Microbiology. In 2019 he was elected to the National Academy of Sciences.