Concentration-Driven Self-Assembly of PS-b-PLA Bottlebrush Diblock Copolymers in Solution

Abstract

Bottlebrush polymers are a class of semiflexible, hierarchical macromolecules with unique potential for shape-, architecture-, and composition-based structure–property design. It is now well-established that in dilute to semidilute solution, bottlebrush homopolymers adopt a wormlike conformation, which decreases in extension (persistence length) as the concentration and molecular overlap increase. By comparison, the solution phase self-assembly of bottlebrush diblock copolymers (BBCP) in a good solvent remains poorly understood, despite critical relevance for solution processing of ordered phases and photonic crystals. In this work, we combine small-angle X-ray scattering, coarse-grained simulation, and polymer synthesis to map the equilibrium phase behavior and conformation of a set of large, nearly symmetric PS-b-PLA bottlebrush diblock copolymers in toluene. Three BBCP are synthesized, with side chains of number-averaged molecular weights of 4500 (PS) and 4200 g/mol (PLA) and total backbone degrees of polymerization of 100, 255, and 400 repeat units. The grafting density is one side chain per backbone repeat unit. With increasing concentration in solution, all three polymers progress through a similar structural transition: from dispersed, wormlike chains with concentration-dependent (decreasing) extension, through the onset of disordered PS/PLA compositional fluctuations, to the formation of a long-range ordered lamellar phase. With increasing concentration in the microphase-separated regimes, the domain spacing increases as individual chains partially re-extend due to block immiscibility. Increases in the backbone degree of polymerization lead to changes in the scattering profiles which are consistent with the increased segregation strength. Coarse-grained simulations using an implicit side-chain model are performed, and concentration-dependent self-assembly behavior is qualitatively matched to experiments. Finally, using the polymer with the largest backbone length, we demonstrate that lamellar phases develop a well-defined photonic band gap in solution, which can be tuned across the visible spectrum by varying polymer concentration.

Introduction

Bottlebrush polymers (“molecular bottlebrushes”) and their derivatives are an emerging class of macromolecules comprising densely grafted side chains attached to a common backbone. The bottlebrush architecture has attracted significant attention across the past decade as recent advances in synthesis have made it possible to take advantage of the multiple degrees of freedom in bottlebrush design, with a controllable shape,¹ grafting density,² and incorporation of a wide variety of reported side-chain and backbone chemistries.³ These synthetic advances have in turn enabled the application of bottlebrush derivatives toward a large and growing set of end uses, spanning photonic crystals,⁴⁻⁸ drug delivery,^9,10 and super-soft elastomers¹¹⁻¹⁴ among others.^15,16

A key advantage of bottlebrush polymers is in the molecular “width” afforded by densely grafted side chains, whose steric crowding enhances backbone rigidity and leads the overall molecular contour to adopt a more extended conformation than linear analogues. Melt-phase studies have demonstrated that bottlebrushes with sufficient grafting density^2,17 and side-chain length exhibit substantially reduced entanglements¹⁴ and limited interpenetration of the flexible side chains.¹⁸ Nonetheless, BBCP backbones retain substantial flexibility and are not “rodlike”, with the Kuhn length of the backbone sometimes reported to be approximately equal to the overall molecular diameter.¹⁹⁻²¹ Numerous studies have reported that bottlebrush homopolymers in dilute to semidilute solutions adopt extended (wormlike/semiflexible) conformations,²²⁻²⁷ although the backbone stiffness (expressed as the Kuhn length or persistence length) is strongly dependent on the concentration.^25,28 This latter aspect has been explained theoretically as a result of excluded volume screening at successively smaller length scales with increasing molecular overlap.²⁹

The incorporation of chemically distinct side chains to create bottlebrush block copolymers (BBCP) enables spontaneous self-assembly, provided that there is both sufficient molecular mobility and segregation strength. For linear block copolymers, it has been demonstrated that solvent dissolution can significantly impact each of these parameters, with concentration effectively imparting a third axis to the conventional phase diagram.³⁰⁻³² However, the concentration-dependent phase behavior of bottlebrush block copolymer assembly remains understudied, and it remains to be seen how these findings translate to bottlebrush systems. Prior simulation³³⁻³⁵ and theoretical^21,35−37 treatments of bottlebrush block copolymer self-assembly have either focused exclusively on melt self-assembly or considered only extremely small bottlebrushes, which do not assemble at the large (>100 nm) domain sizes relevant to emerging applications such as visible-wavelength photonic crystals. Recent experimental reports on bottlebrush block copolymer solution self-assembly have largely focused on micellization of relatively dilute amphiphilic chains in poor solvents, highlighting the importance of solvent selectivity in driving phase behavior.³⁸⁻⁴⁰

There remains a knowledge gap in the self-assembly of BBCP in good solvents, which are suitable for additive manufacturing of large-area photonic films. Early on in the development of bottlebrush block copolymer photonics, Sveinbjörnsson et al.(5) demonstrated that solvent choice could drastically modify the photonic band gap for PS-b-PLA BBCP films prepared via slow evaporation. In our own prior work, we have demonstrated that one-step rapid solution processing is possible when the starting material is dissolved at a high weight fraction (∼10 wt %) in concentrated solution and that the nonequilibrium transition from the solution-state conformation to the dried film state can be precisely controlled to tune photonic properties.⁷ With collaborators,⁴¹ we have also demonstrated the sensitivity of solution-phase BBCP photonic crystals to shear rate under nonequilibrium processing conditions. Finally, we have recently developed coarse-grained simulation tools capable of modeling the self-assembly of such large, photonic-crystal-forming BBCP.^27,42−44

Herein, we use small-angle X-ray scattering experiments to systematically probe the equilibrium concentration-dependent self-assembly and conformation of diblock BBCP and obtain a comprehensive understanding of their phase behavior in a good solvent, observing an initial decrease in chain extension followed by partial restretching upon microphase separation. By investigating a series of compositionally identical BBCP with varying backbone lengths, we clearly observe the impact of an increasing number of repeat units on the segregation strength, with the onset of microphase separation at a lower concentration for larger molecules. We then apply our coarse-grained simulation and find good qualitative matching to the experimental phase diagram. Finally, we demonstrate the strong concentration dependence of photonic properties of BBCP solutions, with tuning of the photonic band gap across the visible spectrum.

Methods

Synthesis of PS-b-PLA Diblock Bottlebrush Block Copolymers

Well-defined poly(styrene)-b-poly(lactic acid) (PS-b-PLA) diblock bottlebrushes were produced via a previously developed route (Figure 1a–c and Figure S1).^7,41,45 In brief, the methodology involved the synthesis of PS macromonomers via an anionic polymerization of styrene initiated by sec-BuLi and PLA macromonomers via an organocatalyzed DBU ring-opening polymerization of lactide.^1,41,46−50 Sequential-addition ring-opening metathesis polymerization (ROMP) was then used to synthesize the targeted symmetric diblock bottlebrushes. Side-chain molecular weights and dispersities were as follows: for PS, an M_n of 4500 g/mol and a Đ of 1.03; for PLA, an M_n of 4200 g/mol and a Đ of 1.05. The library spanned three different backbone lengths (N_bb = 100, 255, and 400) yielding a total of three samples (additional information can be found in SI Section 1).

Figure 1.

(a) Anionic polymerization of styrene initiated by sec-BuLi followed by the addition of ethylene oxide and exo-5-norbornene acid chloride to yield polystyrene macromonomers (Nor-PS). (b) Organocatalyzed DBU ring-opening polymerization of lactide from exo-5-norbornene-2-methanol to yield polylactic acid macromonomers (Nor-PLA). (c) Sequential-addition ring-opening metathesis polymerization of the macromonomers to yield diblock bottlebrush polymers. (d) Small-angle X-ray scattering (SAXS) data for N255 BBCP in toluene at various concentrations. Curves are vertically shifted for clarity. (e) Characteristic concentration-normalized scattering curves for the three phases observed, taken as a subset of the curves for N255 in (d). S(q) indicates the structure factor peak emerging from interactions between adjacent BBCP molecules regardless of chemical identity, while q* arises from the PS/PLA compositional fluctuations in the disordered phase and from ordered lamellae. (f) Cartoons of the microstructure within each regime corresponding to labels (i)–(iv) in panel (e).

Solution Small-Angle X-ray Scattering (SAXS)

Transmission small-angle X-ray scattering (SAXS) experiments were conducted at beamline 12-ID-B of the Advanced Photon Source at the Argonne National Laboratory (Lemont, IL), with a beam energy of 13.3 keV and the distance between the sample and the Pilatus 2M two-dimensional (2D) detector set to 3.6 m. Q-calibration was performed using a silver behenate standard. Solutions of PS-b-PLA diblock bottlebrush polymers were prepared by direct dissolution in toluene (Fisher Chemical T324-4) at room temperature and stirred for at least 2 h before being allowed to rest for several hours prior to measurement. Solutions were sequentially loaded and irradiated from the lowest to the highest concentration beginning with pure toluene, using a single 1 mm quartz capillary (Charles Supper Company)/Teflon tubing flow cell for each polymer. Reduction of 2D scattering data and background subtraction were performed using the Nika and Irena packages^51,52 developed by J. Illavsky for Igor Pro (WaveMetrics, Lake Oswego, OR). 2D data were sector-averaged to avoid occasionally present sharp reflections from the sample holder. Fitting was performed in SasView using an implementation of the generalized Guinier–Porod (two-layer) model developed by Hammouda⁵³ and previously implemented for SasView by Sunday et al.²⁶

Optical Microscopy and UV–Vis Transmission Measurements of BBCP Solutions

Samples for optical microscopy and UV–vis transmission measurements were prepared using a multistep droplet drying/mixing process. First, a stock solution of the largest BBCP studied (N400) was prepared at 100 mg/mL in toluene. Glass coverslips were sequentially rinsed in toluene, acetone (Fisher Chemical A18-4), and isopropanol (Fisher Chemical A451-4) before being dried using a nitrogen gun. To achieve the target concentration between slides, a series of droplets were added to the center of the slide and allowed to dry before the addition of a final droplet with the required amount of solution for the target concentration. To aid in mixing, a square “well” was made by placing two additional coverslips on the side of the final droplet before covering with the top coverslip to enforce a 1 mm gap. The encased droplet was gently tapped until the sample was fully dissolved, before removal of the coverslip spacers to obtain the final gap size (determined by capillary forces). Optical microscope images were obtained under diffuse (ring) light against a dark background (anodized aluminum). Transmission spectra were collected using a Cary 60 UV–vis instrument (Agilent).

Scanning Electron Microscopy of Freeze-Dried Samples

A concentrated sample (Φ_P = 0.207) was prepared as described above, except that a bare silicon substrate was used in place of one of the glass coverslips. The sample was then plunged into a cryogenic liquid mixture of 37% ethane and 63% propane⁵⁴ and transferred into a dish of liquid nitrogen. While under the liquid nitrogen, the glass coverslip was removed to expose the frozen polymer/solvent film. The frozen sample was then rapidly transferred into a sealed thermal stage (Linkam LTS420), which was initially held at −190 ^°C under a nitrogen atmosphere. The frozen sample was placed under vacuum and continuously monitored via optical microscopy over a period of ∼5 h as the temperature was slowly increased until the solvent was observed to be fully removed (without bulk melting of the film). The prepared samples were then mounted in a cross-sectional holder and imaged using a JEOL JSM-7000F analytical SEM at a low accelerating voltage (2.5 kV).

Simulations

The molecular dynamics simulations in this work were performed in the canonical (NVT) ensemble using a Langevin thermostat in the LAMMPS package.⁵⁵ The coarse-grained model for bottlebrush block copolymers was the same implicit side-chain (ISC) model that we introduced in our prior work,⁴³ which resulted from earlier development on the fine-grained bottlebrush model²⁷ and the wormlike cylinder model.⁴² We kept the model details the same as in the prior work,⁴³ which included a bending potential between connected coarse-grained beads to reflect the stiffness induced by the side chains and a stiff harmonic bonding potential to maintain the contour length; contour length and stiffness were determined from explicit side-chain models parameterized to match with experimental measurements of intrinsic viscosity, as discussed in our prior work.²⁷ In addition, we used a scaling-based, soft pairwise potential to capture bottlebrush–bottlebrush interactions.⁴³ We used a relatively slim (noncubic) simulation box to minimize structural defect formation and obtain a better lamellar morphology in cases where it is a preferred thermodynamic state. For further details of the model, we direct readers to refer to our previous paper.⁴³

In this work, we focused on the systems where the degrees of polymerization of the PS and PLA side chains were 45 and 60 repeat units, respectively. In this case, all interaction parameters were identical to what we used in our prior work.⁴³ To explore a wider spectrum of the backbone length, here, we simplified the model by fixing the ratio of the number of coarse-grained beads between two blocks at 1:1. This would result in a slightly asymmetric block architecture since the coarse-grained beads have a small difference in their sizes, but it is much easier to control the total N_bb in this way rather than choosing discretization differently for all backbone lengths. We varied the total number of coarse-grained beads from 6 (3–3 block ratio) to 22 (11–11 block ratio), corresponding to a range of N_bb from 160 to 587. For all these cases, we covered the concentration range of approximately 10–200 mg/mL (Φ_P = 0.0087 – 0.174).

To quantify the phases of the equilibrated state of each simulation, we used the quantity and the degree of mixing ⟨f_Af_B⟩, as the criteria, which we also introduced in our prior work.⁴³ We will discuss the details of classifying phases in the Results and Discussion section.

Results and Discussion

Synthesis and Characterization of PS-b-PLA Diblock BBCP

A series of three poly(styrene)-b-poly(lactic acid) (PS-b-PLA) bottlebrush polymers were synthesized, with constant side-chain molecular weights of M_n, PS = 4500 g/mol and M_n, PLA = 4200 g/mol and three different backbone degrees of polymerization (N_bb = 100, 255, and 400). These polymers are identified hereafter as N100, N255, and N400, and a reaction scheme is provided in Figure 1a–c. Size-exclusion chromatography (SEC) analysis of all the synthesized samples revealed a high-molecular-weight bimodal peak, in which the major peak was determined to be the targeted diblock polymer (94 wt % of the sample).⁴⁵ In all cases, the diblock bottlebrush presented a narrow molecular-weight distribution of M_w/M_n of 1.05 or below (Table 1). The second peak observed in the reaction was identified to be the first block, homo-polystyrene bottlebrush, which constituted 5 wt % of the samples. Additionally, a trace amount of the residual macromonomer (unfunctionalized PS arms, ∼1 wt %) was observed. These polymer samples were used for all the following material studies.

Table 1. Characterization Data for Poly(styrene)-b-poly(lactic acid) Bottlebrush Block Copolymers^a.

polymer	Mw/Mnb	Mw (kg/mol)c	block lengths of PS:PLAd	weight fraction of the diblock:PS homobottlebrush
N100	1.05	421	49:55	0.95:0.05
N255	1.04	1050	124:141	0.95:0.05
N400	1.05	1780	192:222	0.95:0.05

^aA more detailed description can be found in SI Section 1.

^bCalculated with respect to PS standards.

^cDetermined from triple-detection GPC.

^dSee SI Section 1 for calculation details.

Based on the measured molecular weight and bulk density of PS and PLA, the volume fraction of PS in the neat polymer, ϕ_PS, was determined to be approximately 0.53 for each BBCP. Polymers were dissolved in toluene, which has been reported to be a good solvent for both blocks,^56,57 and concentrations are reported in terms of the total polymer volume fraction (Φ_P) in solution, calculated assuming additivity of the volume of the polymer and the solvent. Volume fraction calculations are provided in SI Section 2.

Determination of Phase Behavior and Conformation from Solution Small-Angle X-ray Scattering

For each of the three synthesized BBCP, a series of solutions at varying concentrations were investigated by small-angle X-ray scattering. In this section, we begin with a qualitative discussion of the scattering features that emerge and a discussion of the identified phase behavior (self-assembly). Then, we use quantitative analysis of the scattering data to probe the accompanying change in molecular conformation and packing. We note that the chosen combination of block chemistries, solvent, and X-ray beam energy results in good contrast across the entire range of volume fractions studied, allowing us to rule out the loss of block contrast as an influence on the measured parameters (SI Section 3).

The phase behavior of BBCP with increasing concentration can be directly assessed from the features present in the small-angle X-ray scattering data. Within the full concentration-dependent series presented for the polymer N255 in Figure 1d, the scattering curve substantially changes its shape with increasing concentration, and we begin by identifying three characteristic curves for classification and discussion (Figure 1e). At low concentrations such as Φ_P = 0.0087 (Figure 1e(i,ii)), the scattering curve is consistent with the well-studied semiflexible (wormlike) form factor scattering for dilute bottlebrush homopolymers^22,23,26,42 and is characterized by features at three distinct length scales. At small length scales (q > 0.08 Å^–1), the scattering is dominated by internal density fluctuations of the side chains (so-called “blob scattering”^22,58). At intermediate length scales (0.02 < q < 0.08 Å^–1), scattering probes the cross-sectional size and stiffness of the molecule, while the largest length scales (q < 0.02 Å^–1) provide information about the overall molecular size. Thus, consideration of the intermediate- and low-q regions is sufficient to glean an understanding of the molecular conformation, which can be described by two size parameters, corresponding to the radius of gyration along the short (R_g1) and long (R_g2) axes of the molecule. In the scattering curves, these length scales manifest as inflection points located at q of 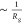. Because scattering curves at these concentrations show no evidence of microphase separation, we label this regime as “uniformly mixed” and comprising dilute–semidilute chains (Figure 1f(i,ii)).

With increasing concentration, the molecular form factor is increasingly obscured through the emergence of two strong structure factor peaks, as clearly shown at Φ_P = 0.118 for the polymer N255 (Figure 1e(iii)). The higher-q structure factor peak (labeled S(q)) becomes sharper and continually shifts toward the right and toward higher q with a further increase in concentration. We interpret this peak as stemming from interactions between adjacent bottlebrushes regardless of chemical identity. As we will discuss later, these interactions between semidilute chains likely begin even at very low concentrations, before the appearance of a clear peak, and it is nontrivial to identify when this interaction first begins to influence the scattering curve. The sharpening of the peak and the shift to smaller length scales can be understood as reflecting an increased crowding of chains in solution. Initially, these interactions occur across the length scale of the overall molecular size; however, as concentration increases and chains begin to pack into microphase-separated structures, the interaction primarily occurs across the radial (side-chain) axis.

The second structure factor peak evident at Φ_P = 0.118 for the polymer N255 appears at lower q (labeled as q* in Figure 1e(iii)) and continues to sharpen and shift leftward (to larger length scales) with a further increase in concentration. Its initial appearance at Φ_P = 0.087 indicates the onset of association of chains based on chemical identity, thus marking the beginning of microphase separation. At this point, a disordered block copolymer phase characterized by PS/PLA compositional fluctuations has formed (Figure 1f(iii)). With a further increase in concentration, this q* peak continues to sharpen and we observe the appearance of multiple higher-order reflections at constant intervals in the q space, consistent with the onset of lamellar ordering⁵⁹ (Figure 1f(iv)) and crossing of the order–disorder transition concentration. The scattering pattern in the ordered phase (Φ_P = 0.305, Figure 1e(iv)) exhibits suppressed intensity of the second-order peak, suggesting that the assembled lamellar structure is nearly symmetric.⁵⁹ As we will discuss further later, the continual leftward shift in q* indicates that the domain size increases with increasing concentration.

We now discuss the full scattering behavior across the series of the three polymers N100, N255, and N400 (Figure 2a). The change in the scattering curve shape with concentration for all three polymers is similar; each exhibits the characteristic form factor of dispersed wormlike chains at low concentrations and forms well-resolved structure factor peaks at higher concentrations. We perform a quantitative comparison of the characteristic length scales in the dispersed and microphase-separated phases in the following section, but we first use the emergence of the distinct scattering features discussed previously to construct the experimental phase diagram shown in Figure 2b. Each polymer follows a similar assembly pathway, although the concentration break points depend on molecular size, a point which we will discuss further below. For all systems, there is a smooth transition between the wormlike chains, disordered PS/PLA compositional fluctuations, and finally (for N255 and N400) the ordered lamellar state, matching the phase behavior previously reported for symmetric linear block copolymers in a neutral good solvent.^30,31

Figure 2.

(a) Concentration-normalized small-angle X-ray scattering (SAXS) data for all three BBCP in toluene. Experimental data points are connected by straight lines to guide the eyes. Symbols and colors are standardized across all three plots to correspond to the volume fractions listed above. (b) Experimental concentration-dependent phase diagram determined from SAXS profiles.

We now focus on examining the change in conformation of the BBCP in the dilute–semidilute regime. The scattering curves for BBCP at low concentrations are shown in Figure 3b. With increasing concentration, there is evident suppression of the slope at low q, which can alternatively be interpreted as a rightward shift in the position of the inflection point (shoulder) corresponding to the overall molecular size R_g2 (in other words, a decrease in molecular extension). However, this anticipated change in molecular extension is nontrivial to interpret, as the emergence of the semidilute concentration correlation length scale (leading to the S(q) peak discussed earlier) will have a similar influence on the scattering profile. In fact, we anticipate both factors to emerge at similar concentration values, as the stiffness of bottlebrush block copolymers arises from excluded volume interaction at multiple length scales. Any concentration dependence of conformation indicates that these low concentrations exceed the overlap concentration and are in the semidilute regime, characterized by the onset of excluded volume screening on the length scale of the bottlebrush contour length.¹⁷ Previous works by Bolisetty et al.(28,60) have also demonstrated that for BBCP, both the semidilute structure factor and the change in polymer conformation influence the scattering profile in the dilute–semidilute regime for bottlebrush homopolymers.

Figure 3.

SAXS data and generalized two-layer Guinier–Porod model fits for BBCP samples under dilute–semidilute conditions. (a) Concentration-normalized scattering data (open symbols) and model fits (solid lines). Curves are normalized by volume fraction. (b) Extracted size parameters using the GGP model. Error bars reflect the 95% credibility interval using the DREAM solver in SasView.

In this work, we follow the fitting approach recently applied by Sunday et al.^25,26 to determine the conformation of PS bottlebrush homopolymers using the shape-independent two-layer generalized Guinier–Porod model (GGP) developed by Hammouda.⁵³ This model allows us to extract R_g1 and R_g2 and two shape parameters s₁ and s₂, which characterize the dimensionality of the molecule and the terminal Porod slope. As recently discussed by Sunday et al.,²⁵ the GGP model exhibits less correlations between fitting parameters compared to the commonly used flexible cylinder model^22,24 and can be augmented (as it is here) with a hard sphere structure factor to partially capture the impact of the structure factor. In this work, we fix s₂ to be 0 and incorporate the hard sphere structure factor if the fitted Porod slope would otherwise exceed the physically limiting value of 4.

The results of fitting the low concentration data with the GGP model are summarized in Figure 3, with fit curves superimposed on concentration-normalized scattering data in Figure 3a, and the extracted size parameters are graphed in Figure 3b. Considering the scattering curves for all three samples, there is always a substantial overlap in the intermediate- and high-q regions, indicating that there is little change in bottlebrush size across the short axis or in the side-chain conformation. This is reflected by the relatively constant values of R_g1 with concentration, ranging from 34.32 ±0.04 to 45.86 ±0.27 nm Å. The lack of variation of R_g1 across the three samples is expected, as they are synthesized at a constant side-chain length. Conversion from R_g1 to the cylinder radius can be made by using the formula for the radius of gyration of a disk-like cross section, resulting in values of the cylinder radius of approximately 4.8–6.5 nm. Considering the overall size and shape of the molecules, we observe that for all three polymers, the intensity at low q decreases with increasing concentration, which is attributable to both the decrease in R_g2 and the influence of the emerging high-q structure factor. At the most dilute concentration studied, only the smallest polymer (N100) exhibited a low-q plateau, meaning that the values of R_g2 determined for the lowest concentrations of N255 and N400 are likely limited by the q range of the experiment and should be taken as lower bounds. Nonetheless, the trend in R_g2 is consistent for all samples: increasing concentration in the uniformly mixed regime leads to an apparent decrease in the overall molecular size, consistent with the behavior of bottlebrush homopolymers.^25,28

We now discuss the behavior of bottlebrush block copolymer samples at higher concentrations, where the onset of compositional fluctuations indicates microphase separation. The differences between the scattering profiles with increasing backbone length are highlighted by plotting scattering profiles for all three polymers on the same axes at fixed concentrations (Figure 4a). Beginning at the lowest concentration (Φ_P = 0.0871), all three polymers exhibit broad correlation peaks indicating the presence of PS/PLA compositional fluctuations in solution. The peak intensity increases with increasing backbone length, and peaks shift to the lower q (higher length scales). At the next higher concentration (Φ_P = 0.118), the sample N400 has formed an ordered lamellar phase, as demonstrated by the weak third-order stacking peak. Finally, at Φ_P = 0.152, both N400 and N255 exhibit lamellar stacking peaks, while N100 remains in the disordered phase. Thus, increasing molecular size increases the segregation strength and drives microphase separation at lower concentrations for larger bottlebrush block copolymers. This effect is also clearly reflected in the experimental phase diagram (Figure 2b), which shows that both the onset of compositional fluctuations and the order–disorder transition concentrations shift to lower concentrations for larger backbone lengths.

Figure 4.

SAXS data for concentrated BBCP solutions exhibiting microphase separation. (a) Scattering data for selected concentrations highlighting the change in the extent of microphase separation with increasing backbone length. Vertical lines indicate centers of PS/PLA block correlation peaks and lamellar stacking peaks. (b) Plot of extracted length scales of compositional fluctuations in the disordered phase and the lamellar d-spacing in the ordered phase. Symbol colors match those of panel (a).

At high concentrations, the clear structure factor peaks substantially obscure the molecular form factor, and we no longer attempt to fit the entire scattering curve. Instead, we infer changes to the molecular conformation with increasing concentration from the changes in the structure factor peak position. A simple measure of the length scale of these features is obtained by dividing the peak position from 2π, and these values are plotted in Figure 4b and Figure S6. The plotted values correspond to the size of PS/PLA compositional fluctuations or the lamellar d-spacing (q*) and the bottlebrush–bottlebrush intermolecular correlation length (S(q)), respectively.

For both features, data for all three polymers follow the same trends. With increasing concentration, the intermolecular correlation length initially decreases sharply and then begins to level off. At the highest concentrations measured, the S(q) intermolecular correlation lengths for N255 and N400 are measured at 9.9 and 11.7 nm, corresponding well to the ∼5 nm cylinder radius calculated previously and suggesting that the brushes of adjacent molecules are not yet interpenetrating at these concentrations. At the larger length scale, there is a monotonic increase in the size of PS/PLA compositional fluctuations/d-spacing with increasing concentration, in qualitative agreement with the measured^31,61 and theoretically predicted⁶² behavior of linear BCP in neutral solvents (Figure S7). Interestingly, the N400 polymer reaches a measured domain spacing of approximately 186 nm at the highest concentration studied (Φ_P = 0.305), which is quite similar to the domain spacing of the neat (solvent-free) polymer when prepared by thermal annealing (187.1 ±2.1 nm).⁶³ This suggests that BBCP backbones are already stretched to near their equilibrium value when there is ∼70% solvent remaining in the system and that for higher concentrations, the competing effects of increasing segregation power and deswelling are nearly balanced. Similar behavior in the d-spacing with concentration has been reported for linear BCP, albeit with the crossover at higher concentrations.⁶¹

Taken together, these trends are fully consistent with the progression illustrated in Figure 1f, where an increasing crowding of backbones along their radial direction occurs simultaneously with extension along their long axes, increasing the domain size. In evaluating the degree of backbone extension, it is helpful to compare the measured domain size versus the contour length of BBCP molecules. We estimate the contour lengths (L_c) of N100, N255, and N400 to be 62, 158, and 248 nm, respectively, using a fixed estimate for the length of the norbornene repeat unit as 0.62 nm²¹ (based on bond geometry). Like linear block copolymers in solution,^31,61,62 BBCP are likely to adopt “bilayer” packing on interface-minimizing grounds, meaning that rodlike extension of BBCP would lead to a d-spacing of ∼2 × L_c. With this context, BBCP in lamellae remain substantially flexible; for all three polymers, the largest measured domain sizes are substantially below their respective L_c. Thus, while chain extension increases with concentration in the ordered phases, BBCP backbones remain substantially flexible and are far from adopting fully extended conformations. This inference is also supported by the simulation data discussed in the following section, which indicates that only those bottlebrush segments immediately adjacent to the block junction are significantly aligned in the direction perpendicular to the interface.

The intermediate degree of backbone stretching observed suggests that there is likely substantial room for modification of the observed polymer conformation and phase diagram via changes to BBCP molecular parameters, such as the backbone grafting density, side-chain length, and the chemical identity (and intrinsic stiffness) of the backbone and side chains. Indeed, several of these factors have already been demonstrated to substantially modify bottlebrush homopolymer conformation^{22−24,27,64,65} in solution, and for large bottlebrushes, this may be a powerful tool for optimizing both the photonic properties discussed below and rheological behavior, which will be important for large-area coating applications.

Coarse-Grained Simulations of BBCP Assembly

The key results of coarse-grained simulations are summarized in Figure 5. We begin by showing a series of simulation snapshots for three values of the backbone length (expressed as the number of backbone repeat units, N_bb), spanning similar concentration ranges (Figure 5a). These numbered snapshots correspond to the labeled points on the overall simulated phase diagram (Figure 5b) and provide a visual confirmation of the phase transition as the concentration changes. The most important feature evident in both the snapshots and the simulated phase diagram is the leftward shift of both phase boundaries (the uniformly mixed phase to the compositional fluctuation regime and the compositional fluctuation regime to the lamellar phase) with increasing backbone length. The χN parameter in classic block copolymer systems serves as a useful analogue since microphase separation is more likely to happen when the two chemically different blocks become longer. In distinguishing the uniformly mixed phase and the disordered, compositionally fluctuating phase, we first applied the same criteria as in our prior work⁴³ (degree of mixing ⟨f_Af_B⟩ equals to ∼0.85). Here, however, we find that some cases that show the characteristic scattering function of compositional fluctuations in experiments are not classified correctly. We located these cases by using a soft ⟨f_Af_B⟩ threshold of 0.85–0.90, which we mark as the “weakly fluctuating” phase in Figure 5b. We attribute this discrepancy to the absence of structural information on the length scale of side chains in the ISC model. We also note that for the lowest N_bb chain simulated, we only observe the uniformly mixed phase, even at the highest concentration that we considered (with or without the soft threshold). This is not in agreement with the experiments; however, this is to be expected because the ISC model is built under the assumption that the bottlebrush is relatively long, and we anticipate there to be end effects not accounted for in the scaling-based potential. Notwithstanding these limitations, we overall find good qualitative agreement between simulated and experimental phase behavior.

Figure 5.

Results of coarse-grained simulations of BBCP with varying backbone lengths. (a) Simulation snapshots for three backbone lengths at varying concentrations, with each image labeled to correspond to a point in the phase diagram in panel (b). (b) Overall phase diagram obtained from simulations. (c) Top: coarse-grained chains within a lamellar phase simulated at N_bb = 400 and Φ_P = 0.157 (b). Bottom: averaged probability distribution for the location of individual A-block coarse-grained beads plotted against the dimensionless position within the A domain. Data points are connected by straight lines to guide the eyes.

Finally, we compute the positional probability distribution of bottlebrush segments within the observed “bilayer” lamellar domains (Figure 5c), using simulation data generated in our previous work⁴³ for N_bb = 400 and Φ_P = 0.157. The quantity p_A,i is a normalized probability distribution function for each bottlebrush coarse-grained segment (averaged over all chains) plotted with respect to the normalized distance perpendicular to the lamellar interface (z), where z = 0 and 1 represent the block junctions. Here, the A-block corresponds to polystyrene, and i is the segment index, with the segment nearest to the block junction point marked in red and the furthest from the junction (the terminal segment) in violet. As can be seen in Figure 5c, the first two segments close to the block junction point exhibit bimodal distributions, with peaks centered near the lamellar interface. All other segments exhibit positional probability distributions with a broad peak in the center of the domain. The similarity in the profiles for beads 3–8 indicates that their locations are not strongly affected by their position along the backbone chain. These results can be attributed to the fact that the beads closer to the interface are the most “localized” due to their connection to the other block, while the end beads are freer to explore the domain. In addition, we calculate the end-to-end distance for chains in the lamellar phase regime and obtain a result of ∼163 nm for the N_bb = 400 case. This is much smaller than the contour length of 248 nm, consistent with the experimental observation that the chains are not fully stretched, and similar to the length scales from SAXS in Figure 4b. Thus, the simulation results support the inference that assembled lamellae comprise “bilayers” of bottlebrush chains that are not significantly stretched, even at high concentrations.

We note that the ISC model has several important limitations. First, the model assumes constant stiffness of the chain under all concentrations, while excluded volume screening of side chains should affect the stiffness as a function of concentration. Consequently, the R_g2 change of each block observed in the experiments is not resolved in simulation results. Second, the molecular parameters (bottlebrush width, pairwise interactions, etc.) are also based on simple scaling arguments made in our previous study.⁴² We recently demonstrated that explicit side-chain simulations are consistent with the interaction potentials used in the ISC model.⁶⁶ The extent that bottlebrush repulsion is quantitatively stronger between dissimilar blocks remains empirically parameterized, as discussed in our prior work.⁴³ Despite these limitations, the current ISC model is mostly successful in capturing the overall concentration dependency of bottlebrush solution assembly.

Photonic Properties of Concentrated BBCP Solutions

Finally, we present the vivid, concentration-dependent photonic properties of concentrated solutions of the largest BBCP studied (N400, Figure 6a). Due to challenges in mixing the highly viscous solutions that are obtained at high volume fractions and to avoid evaporation of the solvent during measurement, bulk solutions were not prepared. Instead, small (∼μL) samples were prepared between glass coverslips using a droplet drying method. Visual observations are supported by UV–vis transmission spectra (Figure 6b), which reveal sharp peaks corresponding to formation of well-defined photonic band gaps. Here, although peaks are measured as “absorption”, all components are optically transparent, and thus, peaks correspond to light reflected out of the beam path. Plotting of the peak position versus concentration confirms that the photonic band gap can be readily tuned across the visible spectrum simply by increasing solution concentration (Figure 6c).

Figure 6.

Photonic properties of concentrated solutions of the bottlebrush block copolymer N400. (a) Optical microscope images of solutions prepared at various volume fractions demonstrating a redshift of the photonic band gap with increasing concentration. (b) Normalized UV–vis transmission spectra for a subset of films corresponding to Φ_P = 0.087,0.113,0.131,0.207,and 0.348 (from left to right). (c) Average peak position (center of the photonic band gap) versus the wavelength computed from measurements of at least three independent samples prepared at each condition. (d) Cross-sectional scanning electron micrograph of a freeze-dried film of a solution prepared at Φ_P = 0.207, showing lamellar ordering.

Consideration of the microstructure of prepared solutions allows us to link the previously discussed SAXS results to the observed photonic properties. First, we confirm the formation of a lamellar morphology in solution via cross-sectional scanning electron microscopy of a freeze-dried film (Figure 6d). The peak reflected wavelength (λ) from a 1D lamellar photonic crystal (at normal incidence) can be linked to layer thickness (d_i) through eq 1,^4,67 where n_i represents the refractive index of the layer, and the d-spacing determined by SAXS is equivalent to the sum of the layer thicknesses.

1

In the case of solvated lamellae, the refractive indices of each layer must be adjusted to account for the presence of the solvent. In the simplest case, assuming equal partitioning of the solvent into each layer, the corrected refractive indices are given by eqs 2 and 3.⁶⁸

2

3

Despite the approximations inherent in this simplified approach, we find good agreement between the measured reflected peak position for the sample prepared at Φ_P = 0.305 (577.8 ± 8.1 nm) and the calculated value of 560.3 nm, determined using the d-spacing measured by SAXS (185.7 nm).

Prior approaches to tuning of the photonic band gap in bottlebrush block copolymer systems have primarily relied on either changing the BBCP molecular weight or by blending with different BBCP, homopolymers, or nanoparticle dopants^4,5,8,69,70 to achieve similar effects. By contrast, the approach of using a solvent to modify photonic properties has commonly been demonstrated for linear block copolymers photonics^67,70 and has the advantage of substantially reducing synthetic efforts and unlocking new dynamic behavior⁴¹ under ambient conditions. When integrated with careful processing control,⁷ solution-based photonic properties can also be systematically varied and preserved during drying into solid films. In bottlebrush systems, the interplay between molecular design, solvent quality, resulting chain extension, and processing drivers is anticipated to provide rich and complex optical behavior and is an exciting target for future study.

Conclusions

In conclusion, we detail the concentration-dependent self-assembly of nearly symmetric PS-b-PLA bottlebrush diblock copolymers in toluene. We use a combination of physical reasoning and coarse-grained simulation to interpret the results of small-angle X-ray scattering data. With increasing concentration from the dilute–semidilute uniformly mixed phase, individual wormlike chains first decrease in extension before transitioning to a regime of increasing chain extension with the onset of compositional fluctuations and the eventual transition to ordered lamellae. Increasing backbone length profoundly impacts the segregation strength, with longer molecules reaching the onset of microphase separation and lamellar ordering at lower concentrations. This effect is qualitatively matched by coarse-grained simulations, with minor deviation in the limit of small backbone lengths due to the inherent limitations of the implicit side-chain model used. For the largest molecule studied, domain sizes in the ordered phase are sufficient to exhibit vivid photonic properties (structural color) with band gaps that are tunable across the visible spectrum simply by varying concentration at equilibrium. These findings are highly relevant for emerging applications of bottlebrush block copolymers prepared via solution processing and provide a critical point of reference for future works exploring bottlebrush diblock copolymer structures under nonequilibrium conditions.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acspolymersau.1c00057.

• Extended materials and characterization methods (SI Section 1), simplified reaction scheme (Figure S1), size-exclusion chromatograms (Figures S2 and S3) and further polymer characterization data (Tables S1–S3), volume fraction calculations, scattering length density and contrast as a function of volume fraction (Figure S4), background-subtracted 1D scattering data (Figure S5), structure factor peak position plotted against concentration (Figure S6), and scaling of lamellar domain size with concentration (Figure S7) (PDF)

Author Contributions

The manuscript was prepared through contributions of all authors. All synthetic procedures and chemical characterization were carried out by D.J.W. with guidance from D.G. Scattering experiments and analysis were led by B.B.P. with assistance from J.J.K., K.S.P., K.P., and Y.C. and guidance from Y.D. Photonic property measurements were performed by Y.C. and B.B.P., with assistance from K.S.P. under the guidance of Y.D. Coarse-grained simulations were designed and carried out by T.P. with guidance from C.E.S. The initial draft of the manuscript was prepared by B.B.P., T.P., and D.J.W. and revised with contributions from all authors. All authors have given approval to the final version of the manuscript.

The authors declare no competing financial interest.