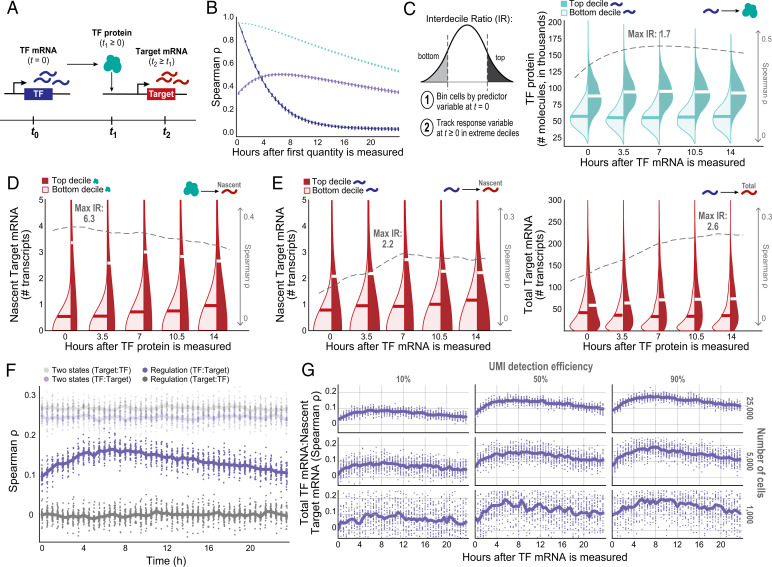
Fig. 3.

Information flow between a TF and its target gene is time-dependent. (A) Schematic of the multistep inference question. (B) TF^(RNA) and TF^(P) Spearman’s ρ autocorrelations and correlations between TF^(RNA) and TF^(P) over time, across 25 simulation runs (each included as its own dot). (C–E) Kernel density estimates comparing the extremes of distributions across cells at t ≥ 0, binned by the predictor molecule abundance at t = 0. Dashed gray line indicates Spearman’s ρ, and “max IR” indicates maximum D10:D1 IR between top- and bottom-binned cells (alternative hypothesis: top decile of the dependent variable is greater than the bottom decile) value at each time point, with the highest magnitude effect listed. (C) TF^(RNA)₀:TF^(P)_T correlation and D10:D1 IR of TF^(P) distribution extremes at t ≥ 0 for cells binned by TF^(RNA) at t = 0. (D) TF^(P)₀:Target^(kon)_T correlation and D10:D1 IR of adjusted Target^(ΔRNA) distribution extremes for cells binned by TF^(P) at t = 0, under the Hill function model of interaction. (E) Relying on mRNA only—C_T^Δ and TF^(RNA)-binned Target^(ΔRNA) D10:D1 IR (Left) and C_T and Target^(RNA) D10:D1 IR (Right)—to infer regulation over time. (F) Correlation between a TF and its putative Target could be a result of cell-state-based structure; if so, the time-shifted correlation would have a stable magnitude over time. (G) Effect of down-sampling the number of cells and/or UMI detection efficiency on estimated TF:Target covariation trends over time (focusing on C_T^Δ). Estimates get both noisier and lower in magnitude due to these two technical considerations.