Skip to main content
PMC home page
Nanoscale Advances logoLink to Nanoscale Advances
. 2019 Dec 23;2(1):190–198. doi: 10.1039/c9na00621d

Probing mechanical properties and failure mechanisms of fibrils of self-assembling peptides†

Federico Fontana 1, Fabrizio Gelain 1,2,✉
PMCID: PMC9416940  PMID: 36133966

Abstract

Self-assembling peptides (SAPs) are a promising class of biomaterials amenable to easy molecular design and functionalization. Despite their increasing usage in regenerative medicine, a detailed analysis of their biomechanics at the nanoscale level is still missing. In this work, we propose and validate, in all-atom dynamics, a coarse-grained model to elucidate strain distribution, failure mechanisms and biomechanical effects of functionalization of two SAPs when subjected to both axial stretching and bending forces. We highlight different failure mechanisms for fibril seeds and fibrils, as well as the negligible contribution of the chosen functional motif to the overall system rupture. This approach could lay the basis for the development of “more” coarse-grained models in the long pathway connecting SAP sequences and hydrogel mechanical properties.

Nano-mechanical characterization of SAPs described in this work combines steered molecular dynamics simulations and Morphoscanner, elucidating failure mechanisms of SAPs fibrils.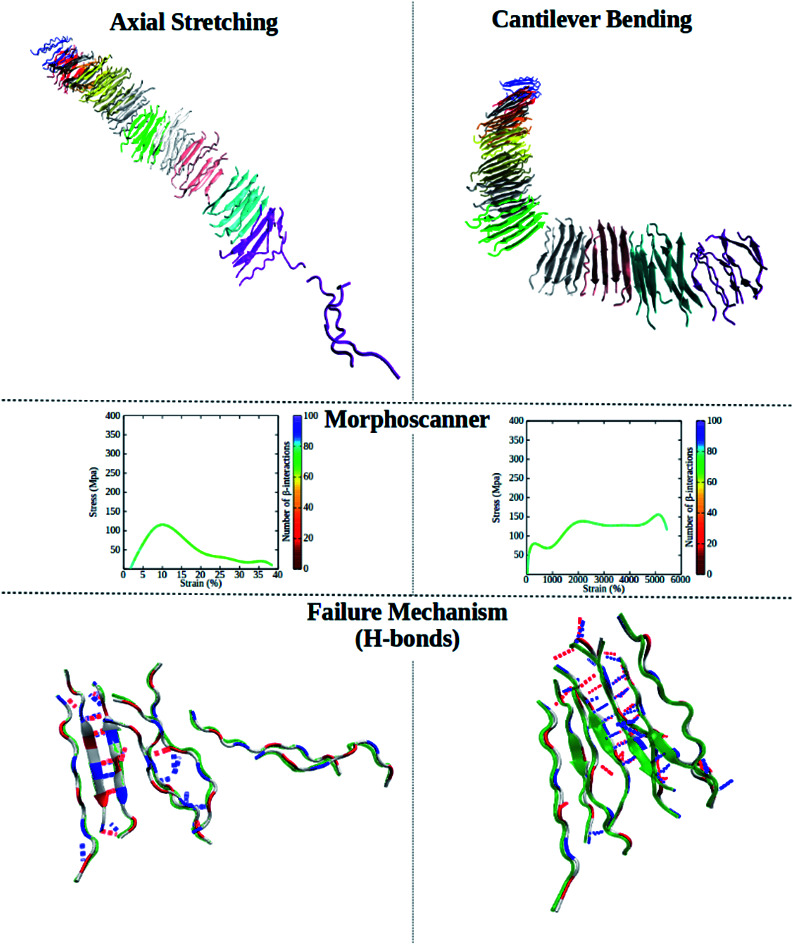graphic file with name c9na00621d-ga.jpg

Introduction

Bio-molecular self-assembly has inspired the so-called “bottom–up” approach to design self-assembling biomaterials.1–6 Among them, self-assembling peptides (SAPs) were adopted to investigate crucial issues in different scientific fields, e.g. the investigation of the mechanisms ruling abiogenesis and Alzheimer's disease in biology, or solar energy harvesting in electronics and regenerative medicine applications in biomaterials science.3,7,8 Furthermore, SAPs have been exploited for tissue engineering applications thanks to their favorable biocompatibility, tailorability and biomimetic properties.6,9–11 Indeed, SAPs have been used in neural tissue engineering for the treatment of brain injury and spinal cord injury (SCI):9–11i.e. SAPs were tested as hydrogel scaffolds capable of spatially guiding regenerating nervous tissues and creating suitable microenvironments for nerve regeneration. However, additional tissue engineering applications of SAP hydrogels are limited by weak control/prediction of their mechanical properties, given by usually reversible and temporary non-covalent interactions at the molecular and nano-scale levels. Despite the recent remarkable progress in nanomechanics, a straight correlation between SAP nanostructural organization and mechanical features is still missing.12,13 On one hand, atomistic and coarse-grained (CG) molecular dynamics (MD) simulations have been used, in combination with empirical experiments, to elucidate the self-assembly pathways and structuring propensities of several peptide sequences at the nanoscale level.13–17 On the other hand, steered molecular dynamics (SMD) simulations have been efficiently adopted to investigate the mechanical properties of biomacromolecular structures such as axial and torsional rigidities.18–20 To cope with limited computational resources, several CG force fields were developed and tested. Among them, the MARTINI force field, initially developed for the investigation of lipid assemblies, was largely used for the investigation of protein and peptide systems, providing interesting insights into structuring phenomena in even larger multi-molecular systems.21–25 Nonetheless, the MARTINI SMD approach found limited applications, because it does not allow conformational transitions26,27 that are quite common in the biological system instead. On the other hand, GoMARTINI overcomes the main limitation of the MARTINI approach, allowing us to track conformational transitions.28 In order to elucidate the structure–mechanics relationship of peptide systems at the nano- and micro-scales, we here propose and validate an innovative fine-to-coarse molecular modeling approach. SAP structuring and mechanical features of the obtained fibrils have been investigated through both atomistic and GoMARTINI-based MD simulations. Atomistic and GoMARTINI-based SMD simulations, analyzed through the recently developed software dubbed Morphoscanner,29 provided comparable results despite the different computing times required and provided insights into the length-dependent failure mechanism of SAP fibrils, opening new opportunities in the field of nanomechanics, laying the foundation for the building of reliable mesoscale models.

Results and discussion

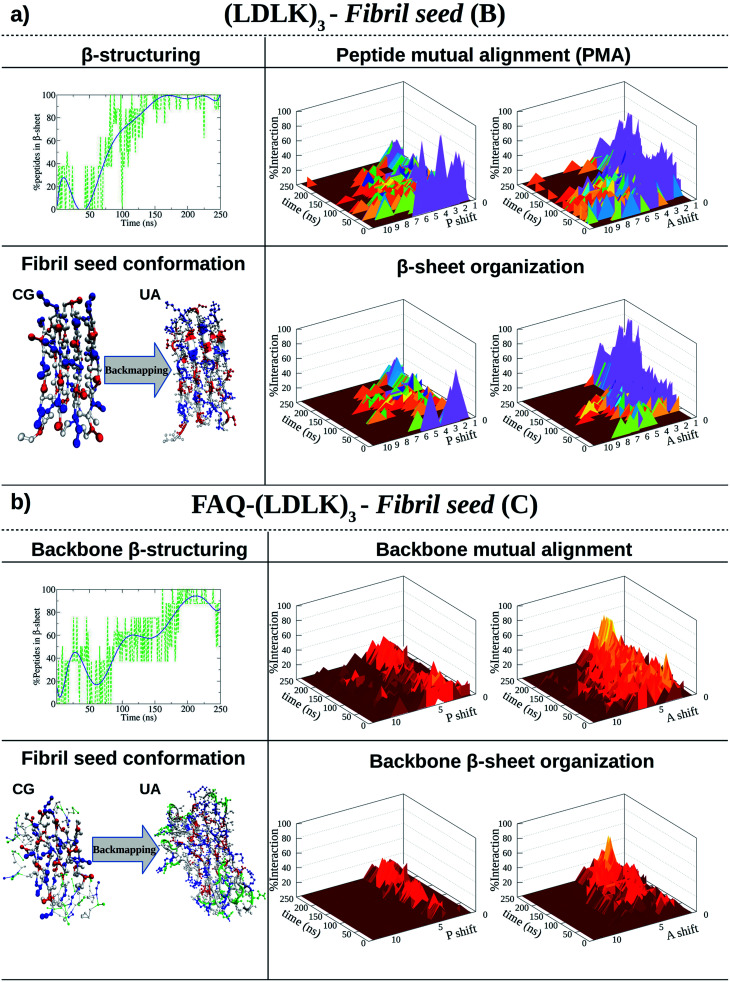
The self-assembling and β-structuring propensity of (LDLK)3 SAPs were investigated using MARTINI CG-MD simulations and Morphoscanner (see Table S1† and Fig. 1a).24,29

Fig. 1. Shift profiles and β-structuring propensity of (LDLK)3-derived SAPs. P refers to parallel alignment and A refers to anti-parallel alignment. The resulting structures from CG-MD were back-mapped and then used as starting conformations for SMD simulations. (a) In 150 ns, (LDLK)3 SAPs aggregate into stable double-layered β-sheet structures (Morphoscanner analysis, see Section 1.7 of the ESI†), yielding strong anti-parallel alignments. Such a tendency was likely due to the electrostatic interactions among oppositely charged side chains of lysine and aspartic acid residues. (b) Alignment analysis of FAQ-(LDLK)3 backbones showed weaker alignments in both A and P, mirrored by lower β-sheet organization. This feature was likely due to the presence of the FAQ functional motif at N-termini, which may have interfered with β-sheet formation among self-assembling backbones.

Fig. 1

Open in a new tab

As shown in Fig. 1a, (LDLK)3 octameric systems (i.e. fibril seeds), assembled preferentially into the double-layered β-sheet structure within 150 ns, and their β-sheet organization were depicted in peptide mutual alignment (PMA) graphs, describing antiparallel alignments. However, (LDLK)3 peptides were also aligned in parallel out-of-register of one-residue resulting in a less ordered double-layered β-sheet structure (Fig. S1 and S2†). Indeed, in-register parallel alignment implied repulsive interactions among identically charged side chains resulting in slow self-assembly kinetics and lower β-structuring propensity (Fig. S1 and S2†).

To investigate the native supramolecular organization of (LDLK)3 fibrils (100-mer), a 20 μs-long one-pot CG-MD simulation has been performed according to the data reported in Table S1.† Each fibril seed (8-mer), obtained through the CG-MD simulation (Fig. 1a), was mapped according to the GoMARTINI model, whereas monomers were mapped according to the standard MARTINI model.25,28 GoMARTINI partially exceeded the main drawback of the MARTINI model allowing us to monitor secondary structure transitions. Indeed, the GoMARTINI model has proven to be suitable for the investigation of peptide/protein folding and unfolding processes.28

As shown in Fig. S3,† in a one-pot CG-MD simulation, the formation of oligomers has been driven by the presence of preformed fibril seeds, resulting in fast self-assembly kinetics, where monomers incorporated into the fibril seed surfaces instead of aggregating into globular clusters.

PMA within fibril seeds influenced the overall peptide alignment within fibrils. Indeed, SAPs within fibrils were also preferentially antiparallel aligned (Fig. 1a and S3†). Such a high degree of order was reflected in a strong β-sheet organization and testified by the growing trend of the nematic order parameter, beyond the threshold value of 0.5 (Fig. S3†). These tendencies were ascribable to the presence of alternating oppositely charged side chains of Lys and Asp, leading to the formation of stable double-layered β-sheet structures.

(LDLK)3 SAPs were functionalized by linking the FAQ sequence at the N-terminus because of its relevance for nerve regeneration.11

FAQ functional motif (alone) self-assembling propensity was evaluated through UA-MD simulations (see Table S2†). Morphoscanner analysis revealed good aggregation but weak β-structuring propensity of FAQ motifs (see Fig. S4–S6†): the formation of well-ordered double-layered β-sheet structures was likely hampered by the presence of Pro residues.

This tendency affected FAQ-(LDLK)3 self-assembly and β-structuring scenario. Indeed, the backbone moieties of the functionalized peptide showed weaker anti-parallel alignment, whereas functional motifs did not assemble into ordered structures (Fig. 1b and S11†). However, FAQ functional motif aggregation features interfere with the formation of well-ordered aggregates. In one case, FAQ functionalization led to slower aggregation kinetics and to lower β-structuring propensity (Fig. S7 and S9†). In another simulation, FAQ functionalization altered the formation of the double-layered β-sheet structure leading to an orthogonal orientation of the β-sheets (Fig. S8 and S10†).

The above-mentioned structures were backmapped, and then two sets of steered molecular dynamics (SMD) simulations, named axial stretching and bending, have been conducted using Gromos53a6 and GoMARTINI force-fields (see Tables S3 and S4†).30–33 In the axial stretching scenario, a constant force has been applied at one end of the fibril seed while the other end remained fixed. Instead, in the bending scenario, a constant lateral force has been applied to the unrestrained end of the fibril seed. These set-ups aimed to mimic the biological assays used in single-molecule experiments to assess the mechanical properties (or the persistence length) of bio-filaments. SMD simulations have been used to obtain additional nanoscale details hardly available from single-molecule spectroscopy experiments, (e.g. non-covalent interaction interplay occurring within protein folding transitions) (see Tables S3 and S4†).33 Indeed, such experiments have been used to (1) compare and validate the GoMARTINI approach against the Gromos53a6 one (see Tables S5–S7†)28 and (2) to classify the bending failure mechanisms of peptide seeds and fibrils related to hydrogen bond and non-covalent interaction deformations (see Tables S8–S9†).33,34

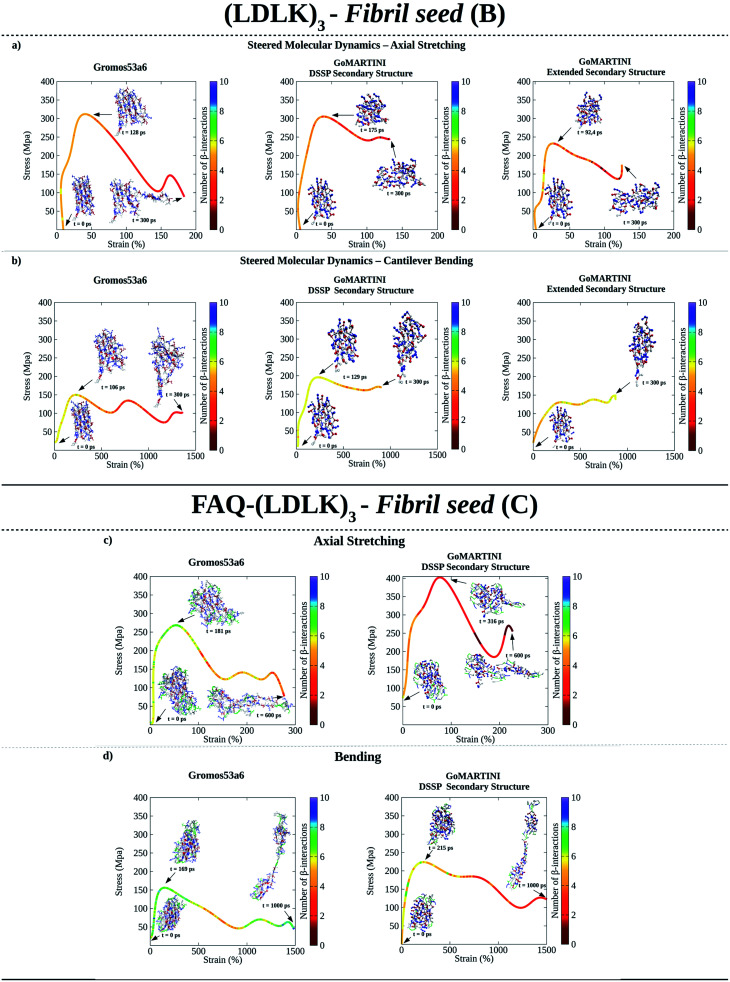
As shown in Fig. 2a, UA-SMD and CG-SMD axial stretching simulations identified different failure conformations of the (LDLK)3 fibril seed. Indeed, in UA-SMD the failure took place at the maximum stress of 323 MPa (ε = 52%), whereas in GoMARTINI it happened at 310 MPa (ε = 28%) and 236 MPa (ε = 36%) for SS parameters assigned through DSSP or as all-extended respectively (see also Tables S5 and S6†).

Fig. 2. Computational nanomechanics characterization of SAP fibril seeds. The number of β-interactions refers to the number of β-contacts among (LDLK)3 moieties identified through Morphoscanner (see Section 1.7 of the ESI†). (a) UA-SMD maximum stress of axial stretching was equal to 323 MPa (ε = 52%; t = 128 ps; no of β-interactions = 6). GoMARTINI maximum stress was influenced by SS assignment: in the case of DSSP SS assignment, the maximum stress was equal to 310 MPa (ε = 28%; t = 175 ps; no of β-interactions = 6), whereas with extended SS parameters, it was equal to 236 MPa (ε = 36%; t = 92 ps; no of β-interactions = 6). (b) UA-SMD axial bending maximum stress was equal to 163 MPa (ε = 250%; t = 106 ps; no of β-interactions = 6). Again, maximum stress in GoMARTINI was heavily affected by SS parameters: i.e. it was 200 MPa (ε = 250%) and 150 MPa (ε = 1000%) for respectively DSSP-assigned and extended SS parameters. (c) UA-SMD axial stretching test highlighted the failure conformation and stress value for FAQ-(LDLK)3 at 281 MPa (ε = 50%). Such a conformation was similar to the one identified through GoMARTINI (σ = 400 MPa; ε = 75%). In the case of FAQ-(LDLK)3, DSSP assigned the extended SS parameters to the (LDLK)3 self-assembling backbone, whereas it assigned random coil SS parameters to residues comprising the functional motif. (d) UA-SMD axial bending maximum stress was equal to 160 MPa (ε = 50%). Instead, GoMARTINI maximum stress was 247 MPa (ε = 220%).

Fig. 2

Open in a new tab

Despite these differences, failure conformations were characterized by the same number of β-interactions (i.e.ref. 6), suggesting similar failure mechanisms. However, it became clear that MARTINI bead-type assignment significantly influenced the elastic moduli of (LDLK)3 seeds in GoMARTINI. Indeed, the assignment of backbone and side-chain beads corresponding to coiled secondary structures (SSs) overestimated the overall elastic modulus values detected with extended SS parameters, (Table S5 and Fig. S12a†).22 Similarly, in bending tests, aimed at estimating the shear moduli (Fig. 2b and S12c†), Morphoscanner analysis at failure revealed comparable β-sheet arrangements of the fibril seeds, while failure stresses in UA-SMD and GoMARTINI simulations were 163 MPa (ε = 250%) and 200 MPa/150 MPa (ε = 250% and SS parameters assigned via DSSP/ε = 1000% and all-extended SS parameters) (see Tables S5 and S6†). Different ε values observed in GoMARTINI simulations were attributable to the level of interactions (pointing at the Lennard-Jones potential well depth) among MARTINI grains. In more detail, the DSSP algorithm assigned random coil SS parameters to (LDLK)3 backbone grains, resulting in polar backbone grains. Instead, when extended SS parameters were assigned, the backbone grains were modeled as non-polar. The interactions among polar grains are stronger than the interactions among non-polar grains.21 This implied a general increase of fibril stiffness for (LDLK)3 when GoMARTINI mapping via DSSP yielded SS parameters set to random coil conformation. By comparing the average elastic modulus and shear modulus of each fibril seed we extracted the shear contribution ratio, a value pointing at the strain distribution within the fibril seeds (see Table S8†).33 In both UA-SMD and GoMARTINI SMD, the shear contribution ratio described similar bending failure mechanisms within (LDLK)3 fibril seeds. Indeed, as shown in Table S8,† the (LDLK)3 bending failure was predominantly dominated by shear stresses, where non-covalent interactions stretched orthogonally to their directions. Moreover, the axial stretching depicted in UA-SMD stress–strain curves showed multiple peaks owing to a slip-stick motion taking place only when interacting surfaces in β-sheet nanocrystals (adjacent β-strands) are rigidly stabilized and act cooperatively. Such a feature was less evident in GoMARTINI-SMD stress–strain curves, probably due to the smoother energy function describing the interactions among grains in the MARTINI model.21,22,28,33

The failure conformations of FAQ-(LDLK)3 fibril seeds showed also small differences between the adopted modeling approaches (see Table S7†), with axial stretching failure conformations at maximum stresses of 281 MPa (ε = 50%) and 400 MPa (ε = 75%) in UA-SMD and CG-SMD simulations respectively (Fig. 2c). In addition, bending stress values were 160 MPa (ε = 50%) and 247 MPa (ε = 220%) in UA-SMD and CG-SMD simulations respectively (Fig. 2d). These values were similar to those observed in the simulations of (LDLK)3 seeds. Such evidence, due to the similar SS parameter assignments, suggested that the presence of the functional motif slightly affected the failure mechanism of SAP fibril seeds.

This observation was corroborated by Morphoscanner analysis and by shear contribution ratio calculation, identifying similar bending failure mechanisms (Table S9†) for both FAQ-(LDLK)3 and (LDLK)3, mainly led by shear stresses.

To elucidate the failure mechanisms of SAP fibrils, two fibril models, resembling the geometry of amyloid fibrils,12,35 were built taking into account the outcome analysis of one-pot CG-MD (Fig. S3†) and tested through the SMD approach (see Tables S3 and S4†). The initial structure of the (LDLK)3 fibril was imposed by patching multiple fibril seeds sharing the molecular conformation shown in Fig. 1a. Also, in the case of FAQ-(LDLK)3, UA-MD simulations pointed out that FAQ functionalization weakly affects the (LDLK)3 moieties' alignment (Fig. S4–S6†). Then, keeping in mind the results from one-pot CG-MD (Fig. S3†) of (LDLK)3, we postulated that, also for FAQ-(LDLK)3, alignment within fibrils resembled that observed in fibril seeds (Fig. 1b).

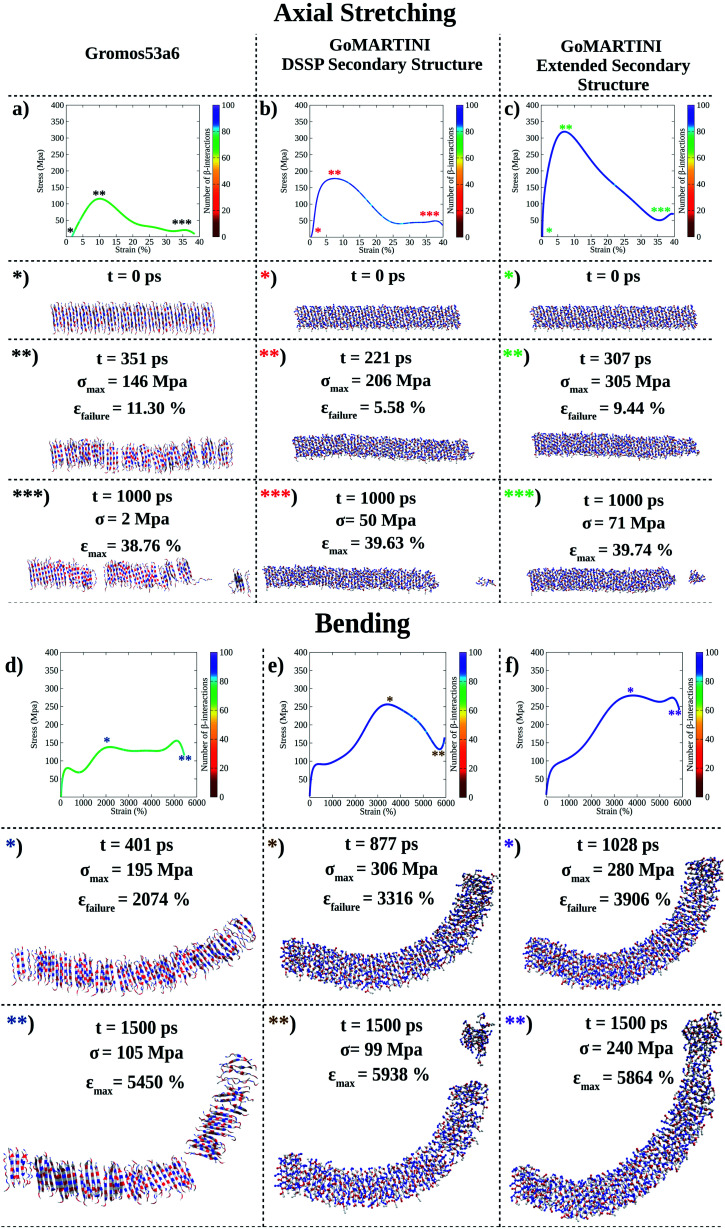
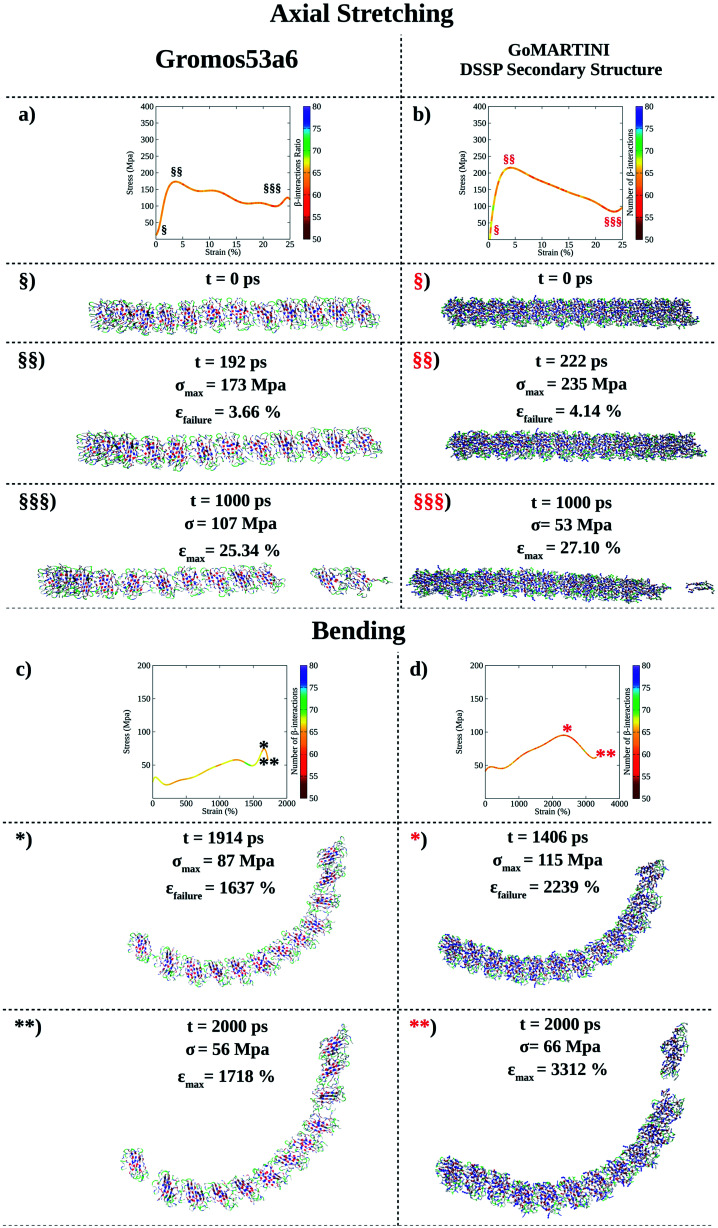
(LDLK)3 fibril conformations at failure, as shown for fibril seeds, were heavily affected by SS assignment (see Tables S5 and S6†). Indeed, CG-SMD axial stretching simulations overestimated the average Young's modulus (E) (Fig. S12b†) found in UA-SMD (Fig. 3a–c), whereas CG-SMD bending simulations provided comparable shear modulus (G) values (Fig. S12d†) to those detected from UA-SMD (Fig. 3d–f). By comparing the average elastic and shear moduli of the (LDLK)3 fibril, the bending failure mechanism was predominantly dominated by the deformation of non-covalent interactions along the fibril direction (Table S8†). The same tendencies have been also observed in the FAQ-(LDLK)3 fibril (Fig. 4a–d, S12f, h and Table S9†).

Fig. 3. Computational nanomechanics characterization of the (LDLK)3 fibril. The number of β-interactions refers to the number of β-contacts detected among (LDLK)3 backbones. (a) UA-SMD axial stretching failure stress was 146 MPa. In GoMARTINI, the maximum stress was influenced by SS parameter assignments: (b) in the case of DSSP-derived SS parameters, the maximum stress was equal to 206 MPa, (c) whereas with extended SS parameters, it was 305 MPa. (d) UA-SMD axial bending failure stress was equal to 195 MPa. As expected, in GoMARTINI, the maximum stress was again heavily affected by SS assignment: (e) with DSSP it was equal to 306 MPa, (f) while with extended SS parameters it was 280 MPa. In the detected failure conformations in UA-SMD simulations, fibrils display multiple rupture points; this may be due to the enhanced stability of β-sheet structures when modeled with the Gromos force field. This was also demonstrated through Morphoscanner analysis (see Section 1.7 of the ESI for details†), which identified the same number of β-interactions throughout UA-SMD simulations. This feature was not reflected in GO-SMD simulations. Indeed, Morphoscanner identified small variations in the number of β-interactions.

Fig. 3

Open in a new tab

Fig. 4. Computational nanomechanics characterization of the FAQ-(LDLK)3 fibril. The number of β-interactions refers to the β-contacts among (LDLK)3 backbones detected with Morphoscanner (see Section 1.7 of the ESI†). (a) UA-SMD axial stretching maximum stress was 192 MPa. (b) GoMARTINI maximum stress was equal to 235 MPa. (c) UA-SMD axial bending maximum stress was 87 MPa. (d) Instead, GoMARTINI maximum stress was equal to 115 MPa. As shown for (LDLK)3 fibrils, Morphoscanner identified a constant number of β-interactions in UA-SMD simulations, whereas it identified little variation in CG-SMD simulations: this can be ascribable to the more fragile rupture observed in UA-SMD simulations.

Fig. 4

Open in a new tab

The evidence from the atomistic model demonstrated that the strain distribution characterizing the bending failure mechanism of SAP nano-filaments is length-dependent and mainly influenced by the geometrical properties of peptide aggregates.9,14,15,33 Despite the influence of CG bead types on elastic and shear moduli, similar evidence was also confirmed in the CG model. The fibril bending failure was dominated by the deformation of non-covalent interactions along the fibril direction (see Tables S8 and S9†).

Interestingly, the FAQRVPP functional motif did not contribute significantly to the Young and shear moduli of the fibril seeds: this was the case for both UA-SMD and CG-SMD (Fig. S12a, e, c and g†). Consequently, in FAQ-(LDLK)3 fibrils as well, the strain distribution was predominantly influenced by the length of peptide assemblies (Fig. S12b, d, f and h†). Indeed, as shown in Tables S8 and S9,† in the investigated fibril seeds, the shear contribution ratio pointed out that shear deformations were predominant in bending deformations, whereas in fibril systems, the shear deformations contributed less than 15% over the total bending deformations. Such evidence clearly shows that the shear strain distribution is less homogeneous in fibrils than in fibril seeds, causing the propagation of several structural defects in fibrils (see Fig. 2–4). Finally, fibril failure mechanisms have not been affected by stacking fibril seeds next to each other (Fig. S13†).

Conclusions

In the present study, SMD simulations have been used to investigate the mechanical features of (LDLK)3 and FAQ-(LDLK)3 SAPs. The evidence from SMD simulations pointed out that the shear modulus of fibrils is higher in (LDLK)3 than in FAQ-(LDLK)3 (Fig. S12d–h†): such results well correlate with previous rheological data of FAQ-(LDLK)3 and (LDLK)3 hydrogels, featuring a higher shear modulus for (LDLK)3 than for FAQ-(LDLK)3 hydrogels.9,10

In addition, the comparison of the elastic and shear moduli of fibrils demonstrated that bending failure modes depended on the length of the fibrils, while it was less influenced by the presence of the FAQ functional motif. Indeed, fibril seeds' bending failure mechanism was mainly ruled by shear deformation of non-covalent bonds (e.g. H-bonds), whereas fibrils' failure mechanism was led by tensional stretching of non-covalent bonds resulting in multiple failure points.

In summary, the GoMARTINI force-field, provided that the assignment of CG-bead types is crucial for trustworthy results, is suitable for the investigation of key mechanical features of peptidic nanostructures. GoMARTINI-SMD simulations provided comparable results to those obtained through UA-SMD.28 It has also been observed that using the GoMARTINI force-field allows for the reduction of computational costs, accelerating the production phase by about 10 times (Tables S10 and S11†).36 This evidence corroborates the strategy of using GoMARTINI-SMD for the investigation of larger SAP systems and other biomaterials.

Conflicts of interest

There are no conflicts of interest to declare.

Supplementary Material

NA-002-C9NA00621D-s001

Acknowledgments

F. F. and F. G. conceived the project. F. F. performed all experiments and MD simulations. F. F. wrote the Python and R script for the analysis of MD simulations. F. G. supervised the project and acquired funding. F. F. and F. G. wrote the manuscript. We gratefully thank Dr Markus Weingarth at Bijvoet Center for Biomolecular Research (Utrecht University) for supervising ssNMR characterization. The work was funded the “Ricerca Corrente” funding granted by the Ministry of Health, Italy, and by the “5 × 1000” voluntary contributions. Financial support was also provided by Revert Onlus. The secondment of F. F. at Utrecht University was granted by the Erasmus Traineeship Program of University of Milano-Bicocca. ssNMR experiments were also supported by iNEXT.

†

Electronic supplementary information (ESI) available. See DOI: 10.1039/c9na00621d

References

  1. Zhang S. Fabrication of novel biomaterials through molecular self-assembly. Nat. Biotechnol. 2003;21(10):1171–1178. doi: 10.1038/nbt874. [DOI] [PubMed] [Google Scholar]
  2. Whitesides G. M. Grzybowski B. Self-assembly at all scales. Science. 2002;295(5564):2418–2421. doi: 10.1126/science.1070821. [DOI] [PubMed] [Google Scholar]
  3. Krishnamurthy R. Giving Rise to Life: Transition from Prebiotic Chemistry to Protobiology. Acc. Chem. Res. 2017;50(3):455–459. doi: 10.1021/acs.accounts.6b00470. [DOI] [PubMed] [Google Scholar]
  4. Higgs P. G. Chemical Evolution and the Evolutionary Definition of Life. J. Mol. Evol. 2017;84(5–6):225–235. doi: 10.1007/s00239-017-9799-3. [DOI] [PubMed] [Google Scholar]
  5. Mathis C. Bhattacharya T. Walker S. I. The Emergence of Life as a First-Order Phase Transition. Astrobiology. 2017;17(3):266–276. doi: 10.1089/ast.2016.1481. [DOI] [PubMed] [Google Scholar]
  6. Kyle S. Aggeli A. Ingham E. McPherson M. J. Production of self-assembling biomaterials for tissue engineering. Trends Biotechnol. 2009;27(7):423–433. doi: 10.1016/j.tibtech.2009.04.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Smith J. F. Knowles T. P. Dobson C. M. Macphee C. E. Welland M. E. Characterization of the nanoscale properties of individual amyloid fibrils. Proc. Natl. Acad. Sci. U. S. A. 2006;103(43):15806–15811. doi: 10.1073/pnas.0604035103. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Frederix P. Patmanidis I. Marrink S. J. Molecular simulations of self-assembling bio-inspired supramolecular systems and their connection to experiments. Chem. Soc. Rev. 2018;47(10):3470–3489. doi: 10.1039/C8CS00040A. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Pugliese R. Fontana F. Marchini A. Gelain F. Branched peptides integrate into self-assembled nanostructures and enhance biomechanics of peptidic hydrogels. Acta Biomater. 2018;66:258–271. doi: 10.1016/j.actbio.2017.11.026. [DOI] [PubMed] [Google Scholar]
  10. Pugliese R. Maleki M. Zuckermann R. N. Gelain F. Self-assembling peptides cross-linked with genipin: resilient hydrogels and self-standing electrospun scaffolds for tissue engineering applications. Biomater. Sci. 2018;7(1):76–91. doi: 10.1039/C8BM00825F. [DOI] [PubMed] [Google Scholar]
  11. Caprini A. Silva D. Zanoni I. Cunha C. Volonte C. Vescovi A. et al., A novel bioactive peptide: assessing its activity over murine neural stem cells and its potential for neural tissue engineering. New Biotechnol. 2013;30(5):552–562. doi: 10.1016/j.nbt.2013.03.005. [DOI] [PubMed] [Google Scholar]
  12. Choi B. Kim T. Lee S. W. Eom K. Nanomechanical Characterization of Amyloid Fibrils Using Single-Molecule Experiments and Computational Simulations. J. Nanomater. 2016;2016:1–16. [Google Scholar]
  13. Lamour G. Nassar R. Chan P. H. W. Bozkurt G. Li J. Bui J. M. et al., Mapping the Broad Structural and Mechanical Properties of Amyloid Fibrils. Biophys. J. 2017;112(4):584–594. doi: 10.1016/j.bpj.2016.12.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Crowet J. M. Nasir M. N. Dony N. Deschamps A. Stroobant V. Morsomme P. et al., Insight into the Self-Assembling Properties of Peptergents: A Molecular Dynamics Simulation Study. Int. J. Mol. Sci. 2018;19(9):2772. doi: 10.3390/ijms19092772. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Frederix P. W. Ulijn R. V. Hunt N. T. Tuttle T. Virtual Screening for Dipeptide Aggregation: Toward Predictive Tools for Peptide Self-Assembly. J. Phys. Chem. Lett. 2011;2(19):2380–2384. doi: 10.1021/jz2010573. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Fu I. W. Markegard C. B. Nguyen H. D. Solvent effects on kinetic mechanisms of self-assembly by peptide amphiphiles via molecular dynamics simulations. Langmuir. 2015;31(1):315–324. doi: 10.1021/la503399x. [DOI] [PubMed] [Google Scholar]
  17. Saracino G. A. Gelain F. Modelling and analysis of early aggregation events of BMHP1-derived self-assembling peptides. J. Biomol. Struct. Dyn. 2014;32(5):759–775. doi: 10.1080/07391102.2013.790848. [DOI] [PubMed] [Google Scholar]
  18. Bourne J. W. Torzilli P. A. Molecular simulations predict novel collagen conformations during cross-link loading. Matrix Biol. 2011;30(5–6):356–360. doi: 10.1016/j.matbio.2011.03.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Ghodsi H. Darvish K. Investigation of mechanisms of viscoelastic behavior of collagen molecule. J. Mech. Behav. Biomed. Mater. 2015;51:194–204. doi: 10.1016/j.jmbbm.2015.07.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Sotomayor M. Schulten K. Single-molecule experiments in vitro and in silico. Science. 2007;316(5828):1144–1148. doi: 10.1126/science.1137591. [DOI] [PubMed] [Google Scholar]
  21. Marrink S. J. Risselada H. J. Yefimov S. Tieleman D. P. de Vries A. H. The MARTINI force field: coarse grained model for biomolecular simulations. J. Phys. Chem. B. 2007;111(27):7812–7824. doi: 10.1021/jp071097f. [DOI] [PubMed] [Google Scholar]
  22. Monticelli L. Kandasamy S. K. Periole X. Larson R. G. Tieleman D. P. Marrink S. J. The MARTINI Coarse-Grained Force Field: Extension to Proteins. J. Chem. Theory Comput. 2008;4(5):819–834. doi: 10.1021/ct700324x. [DOI] [PubMed] [Google Scholar]
  23. Lien Y. H. Ram Mahato D. Hoppe-Seyler F. Fischer W. B. Membrane partitioning of peptide aggregates: coarse-grained molecular dynamics simulations. J. Biomol. Struct. Dyn. 2019:1–9. doi: 10.1080/07391102.2019.1581660. [DOI] [PubMed] [Google Scholar]
  24. Thota N. Luo Z. Hu Z. Jiang J. Self-assembly of amphiphilic peptide (AF)6H5K15: coarse-grained molecular dynamics simulation. J. Phys. Chem. B. 2013;117(33):9690–9698. doi: 10.1021/jp4059752. [DOI] [PubMed] [Google Scholar]
  25. Xu L. Chen Y. Wang X. Assembly of amyloid beta peptides in the presence of fibril seeds: one-pot coarse-grained molecular dynamics simulations. J. Phys. Chem. B. 2014;118(31):9238–9246. doi: 10.1021/jp505551m. [DOI] [PubMed] [Google Scholar]
  26. Gautieri A. Russo A. Vesentini S. Redaelli A. Buehler M. J. Coarse-Grained Model of Collagen Molecules Using an Extended MARTINI Force Field. J. Chem. Theory Comput. 2010;6(4):1210–1218. doi: 10.1021/ct100015v. [DOI] [Google Scholar]
  27. Kim J. I. Kwon J. Baek I. Na S. Steered molecular dynamics analysis of the role of cofilin in increasing the flexibility of actin filaments. Biophys. Chem. 2016;218:27–35. doi: 10.1016/j.bpc.2016.08.002. [DOI] [PubMed] [Google Scholar]
  28. Poma A. B. Cieplak M. Theodorakis P. E. Combining the MARTINI and Structure-Based Coarse-Grained Approaches for the Molecular Dynamics Studies of Conformational Transitions in Proteins. J. Chem. Theory Comput. 2017;13(3):1366–1374. doi: 10.1021/acs.jctc.6b00986. [DOI] [PubMed] [Google Scholar]
  29. Saracino G. A. A. Fontana F. Jekhmane S. Silva J. M. Weingarth M. Gelain F. Elucidating Self-Assembling Peptide Aggregation via Morphoscanner: A New Tool for Protein-Peptide Structural Characterization. Adv. Sci. 2018;5(8):1800471. doi: 10.1002/advs.201800471. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Wassenaar T. A. Pluhackova K. Bockmann R. A. Marrink S. J. Tieleman D. P. Going Backward: A Flexible Geometric Approach to Reverse Transformation from Coarse Grained to Atomistic Models. J. Chem. Theory Comput. 2014;10(2):676–690. doi: 10.1021/ct400617g. [DOI] [PubMed] [Google Scholar]
  31. Sivaramakrishnan S. Spink B. J. Sim A. Y. Doniach S. Spudich J. A. Dynamic charge interactions create surprising rigidity in the ER/K alpha-helical protein motif. Proc. Natl. Acad. Sci. U. S. A. 2008;105(36):13356–13361. doi: 10.1073/pnas.0806256105. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Xu Z. Paparcone R. Buehler M. J. Alzheimer's abeta(1-40) amyloid fibrils feature size-dependent mechanical properties. Biophys. J. 2010;98(10):2053–2062. doi: 10.1016/j.bpj.2009.12.4317. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Keten S. Xu Z. Ihle B. Buehler M. J. Nanoconfinement controls stiffness, strength and mechanical toughness of beta-sheet crystals in silk. Nat. Mater. 2010;9(4):359–367. doi: 10.1038/nmat2704. [DOI] [PubMed] [Google Scholar]
  34. Oostenbrink C. Soares T. A. van der Vegt N. F. van Gunsteren W. F. Validation of the 53A6 GROMOS force field. Eur. Biophys. J. 2005;34(4):273–284. doi: 10.1007/s00249-004-0448-6. [DOI] [PubMed] [Google Scholar]
  35. Knowles T. P. Fitzpatrick A. W. Meehan S. Mott H. R. Vendruscolo M. Dobson C. M. et al., Role of intermolecular forces in defining material properties of protein nanofibrils. Science. 2007;318(5858):1900–1903. doi: 10.1126/science.1150057. [DOI] [PubMed] [Google Scholar]
  36. Biagini T. Petrizzelli F. Truglio M. Cespa R. Barbieri A. Capocefalo D. et al., Are Gaming-Enabled Graphic Processing Unit Cards Convenient for Molecular Dynamics Simulation? Evol. Bioinf. Online. 2019;15:1176934319850144. doi: 10.1177/1176934319850144. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

NA-002-C9NA00621D-s001
NA-002-C9NA00621D-s001.pdf (2.2MB, pdf)

Articles from Nanoscale Advances are provided here courtesy of Royal Society of Chemistry

RESOURCES