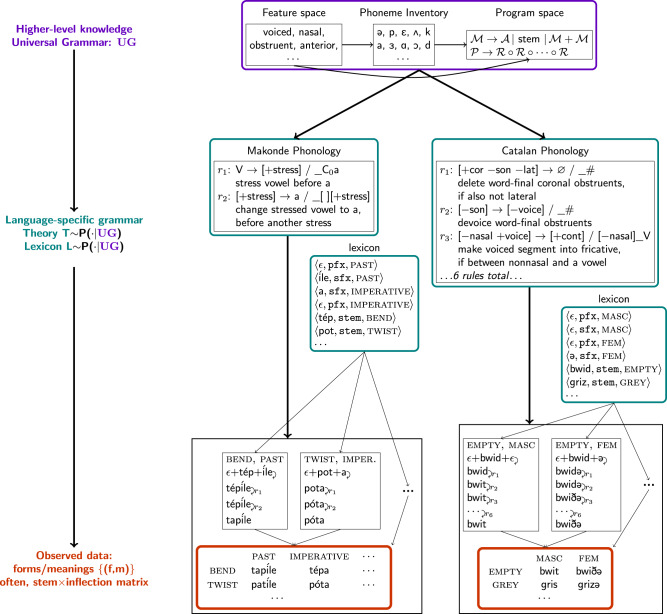
Fig. 2. The generative model underlying our approach.

We infer grammars (teal) for a range of languages, given only form/meaning pairs (orange) and a space of programs (purple). Form/meaning pairs are typically arranged in a stem × inflection matrix. For example, the lower right matrix entry for Catalan means we observe the form/meaning pair ⟨/grizə/,[stem:GREY; gender:FEM]⟩. Grammars include phonology, which transforms concatenations of stems and affixes into the observed surface forms using a sequence of ordered rules, labeled r₁, r₂, etc. The grammar's lexicon contains stems, prefixes, and suffixes, and morphology concatenates different suffixes/prefixes to each stem for each inflection. ϵ refers to the empty string. Each rule is written as a context-dependent rewrite, and beneath it, an English description. In the lower black boxes, we show the inferred derivation of the observed data, i.e. the execution trace of the synthesized program. Grammars are expressed as programs drawn from a universal grammar, or space of allowed programs. Makonde and Catalan are illustrated here. Other examples are in Fig. 4 and Supplementary Figs. 1–3.