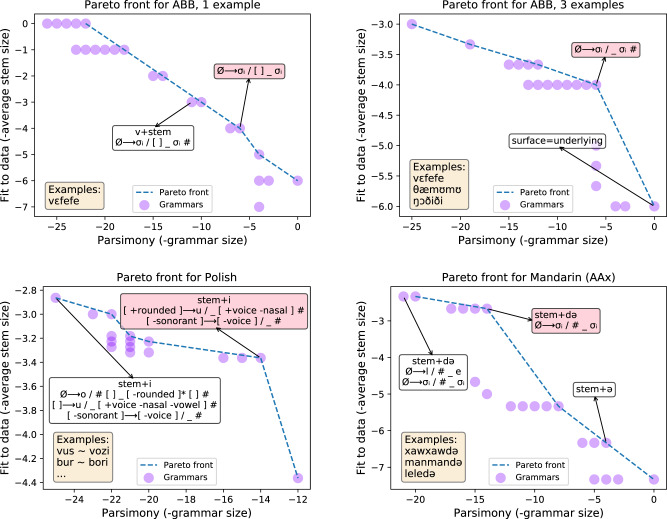
Fig. 7. Modeling ambiguity in language learning.

Few-shot learning of language patterns can be highly ambiguous as to the correct grammar. Here we visualize the geometry of generalization for several natural and artificial grammar learning problems. These visualizations are Pareto frontiers: the set of solutions consistent with the data that optimally trade-off between parsimony and fit to data. We show Pareto fronts for ABB (ref. 39; top two) & AAX (Gerken⁵³; bottom right, data drawn from isomorphic phenomena in Mandarin) AGL problems for either one example word (upper left) or three example words (right column). In the bottom left we show the Pareto frontier for a textbook Polish morpho-phonology problem. Rightward on x-axis corresponds to more parsimonious grammars (smaller rule size + affix size) and upward on y-axis corresponds to grammars that best fit the data (smaller stem size), so the best grammars live in the upper right corners of these graphs. N.B.: Because the grammars and lexica vary in size across panels, the x and y axes have different scales in each panel. Pink shade: correct grammar. As the number of examples increases, the Pareto fronts develop a sharp kink around the correct grammar, which indicates a stronger preference for the correct grammar. With one example the kinks can still exist but are less pronounced. The blue lines provably show the exact contour of the Pareto frontier, up to the bound on the number of rules. This precision is owed to our use of exact constraint solvers. We show the Polish problem because the textbook author accidentally chose data with an unintended extra pattern: all stems vowels are /o/ or /u/, which the upper left solution encodes via an insertion rule. Although the Polish MAP solution is correct, the Pareto frontier can reveal other possible analyses such as this one, thereby serving as a kind of linguistic debugging. Source data are provided as a Source data file.