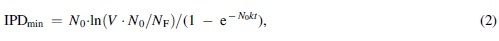Box 3.

Calculating an Inundative Phage Density or Inundative Phage Number

If we assume a constant phage density, then a minimum inundative phage density (IPDmin) can be defined as,

$$IP{D}_{min}=ln\left(V\cdot N_0∕N_F\right)∕kt,$$ (1)

where N0 is the starting concentration of bacteria, V is the volume in which phages are impacting bacteria, NF is the end number of bacteria (not concentration, but still as found over the entire volume), k is the adsorption rate constant, and t is the time over which you want this reduction in numbers of bacteria to occur. Note that the equation alternatively could be written as IPDmin = −ln(NF/V∙N0)/kt (i.e., see Fig. 3). This is based on the minimum bactericidal concentration, of phages, calculation from Abedon.17

If there were 106 bacteria per milliliter in a 10 mL volume, then that would be 107 bacteria in total. If the goal is to reduce that number down to, for example, a total of 10 bacteria over 100 min, then this would require an MOIactual of 13.8, as is equal to ln(107/10) = ln(V∙N0/NF). Assuming a constant phage titer, that would require, per Equation (1), about 5.5 × 107 phages/mL = IPDmin with k here defined, as in Box 1, as 2.5 × 10−9 mL−1 min−1. That is, 5.5 × 107 = 13.8/(2.5 × 10−9 × 100).

The Equation (1) calculation can become less realistic at higher bacterial densities, as rates of phage adsorption increase to a point that phage numbers are substantially reduced over short time frames (again, as considered in Box 1). This in essence is the opposite of the problem of how MOIinput increasingly fails to approximate MOIactual at increasingly lower concentrations of target bacteria.25 That is, here it is associated with substantial phage adsorption rather than too little. A calculation allowing for phage adsorption, holding numbers of adsorbable bacteria constant over time, is however easily generated as a modification of Equation (1). Thus,

which for the same numbers as above is equal instead to 6.2 × 107 = IPDmin, or not much different in this example from the calculated 5.5 × 107 phages/mL delivered by Equation (1). Again, see Abedon17 for more details.

If we change N0 to 108 bacteria per milliliter, then the Equation (2) calculated IPDmin instead would be 1.8 × 109 phages/mL. By contrast, by Equation (1) the IPDmin value for N0 = 108 bacteria per milliliter would be a presumably unrealistically low 7.4 × 107 phages/mL, with the difference owing to the assumption for Equation (1) that phage numbers do not decline despite ongoing phage adsorption to bacteria. That is, with Equation (1) free phage adsorption with free phage replacement is assumed whereas with Equation (2) free phage numbers do decline with phage adsorption (still assumed, though, is no phage replication nor replication of unadsorbed bacteria).

Unfortunately, it is difficult to modify these calculations to consider spatially structured environments such as biofilms. In part, this is because volumes overlying biofilms can range from very tiny to effectively infinite,28 which renders the “density” aspect of IPD irrelevant. What becomes relevant instead are total numbers of phages (PT or IPN, as considered below), total numbers of targeted bacteria (NT), the extent to which the added phages adsorb, and the degree to which phages can reach individual bacteria. Notwithstanding these issues, and assuming that all phages can reach and then adsorb all bacteria easily, then we can revert to considerations of straight Poisson distributions, that is, as covered in the main text (after the heading, “Poisson can be your friends”). Thus, reducing total numbers of biofilm bacteria from 107 down to 10 would again require an MOIactual of 13.8 (see, e.g., Fig. 4), which would require a total of 1.38 × 108 phages (i.e., 13.8 × 107), or what instead could be, for example, 1.38 × 107 phages/mL distributed over 10 mL.

The latter, a minimum inundative phage number (IPNmin), is smaller than that calculated using Equation (2), which instead is 10 mL × 6.2 × 107 phages/mL. This is because all of the phages in the calculation yielding IPNmin = 1.38 × 108 phages, where that calculation basically is,

$$IP{N}_{min}=ln\left(N_T∕N_F\right)\cdot N_T,$$ (3)

are assumed to adsorb. With Equation (2), by contrast, only 22% of phages will have adsorbed over 100 min, and 1.38/0.22 with rounding error is about 6.2. This is 1.38 × 108 phages/mL for IPNmin distributed over 10 mL versus 6.2 × 108 phages/mL for IPDmin also distributed over 10 mL via the Equation (2) calculation. Of course, if a lower fraction of phages adsorb in either example, then higher phage titers will be required to achieve the same amount of killing of bacteria as based on adsorption by the originally dosed phages.

In summary, there exists overall a phage density (a titer, i.e., an IPD) or instead an absolute number of phages (an IPN) that are minimally required to reduce some starting number of bacteria (NT = V∙N0) to some desired ending or final number of bacteria (NF), which in the case of IPD is over some desired interval of time (t). This minimum phage quantity in many cases may be relatively easily approximated. Generally, especially as seen using Equations (2) and (3), the number of phages required (IPD or IPN) also will be somewhat in excess of the number of bacteria targeted, and this is both because it takes time for phages to adsorb and, statistically, many more phage adsorptions are required to infect most or all bacteria than there are bacteria, that is, due to phage adsorptions occurring over Poisson distributions. Note, by the way, that as with Equation (3), if we set t to infinity with Equation (2), then we can rearrange such that the fraction of bacteria not adsorbed (NF/NT or NF/V∙N0) is equal to e−n, where n is MOIactual, that is, as equivalent to IPNmin/N0 or IPDmin/N0. This explicitly is the calculation considered in Box 2, where 100% phage adsorption is implicitly assumed. That is, all of these calculations are based on an assumption that phage populations adsorb bacterial populations Poissonally.

IPD, inundative phage density; IPN, inundative phage number.