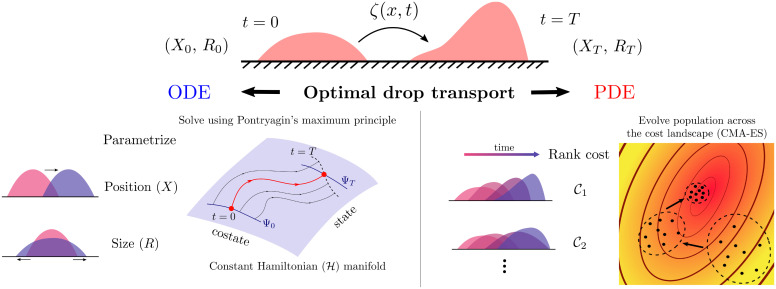
Fig. 1.

Optimal transport of an active drop. A schematic illustrating our framework to solve the problem of transporting an active drop by minimizing a specified cost function, such as the mechanical work. The spatiotemporal profile of activity $\zeta (x,t)$ is the control variable, and the transport task involves moving the drop from position X₀ and size R₀ to a final position X_T and size R_T in a finite time T. We employ two complementary approaches: 1) finite-dimensional optimal control using Pontryagin’s maximum principle on an ODE-based reduced order model that captures parametrized features of the drop; and 2) constrained numerical optimization of the nonlinear continuum PDE using a gradient-free evolutionary algorithm, such as CMA-ES (see PDE Control main text).